第十八章 平行四边形 单元检测试卷(含答案)
文档属性
| 名称 | 第十八章 平行四边形 单元检测试卷(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 467.9KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-04-16 15:44:16 | ||
图片预览

文档简介
第十八章 平行四边形 单元检测试卷2(含答案) 2023--2024学年人教版数学八年级下册
选择题(每小题3分,10小题,共30分)
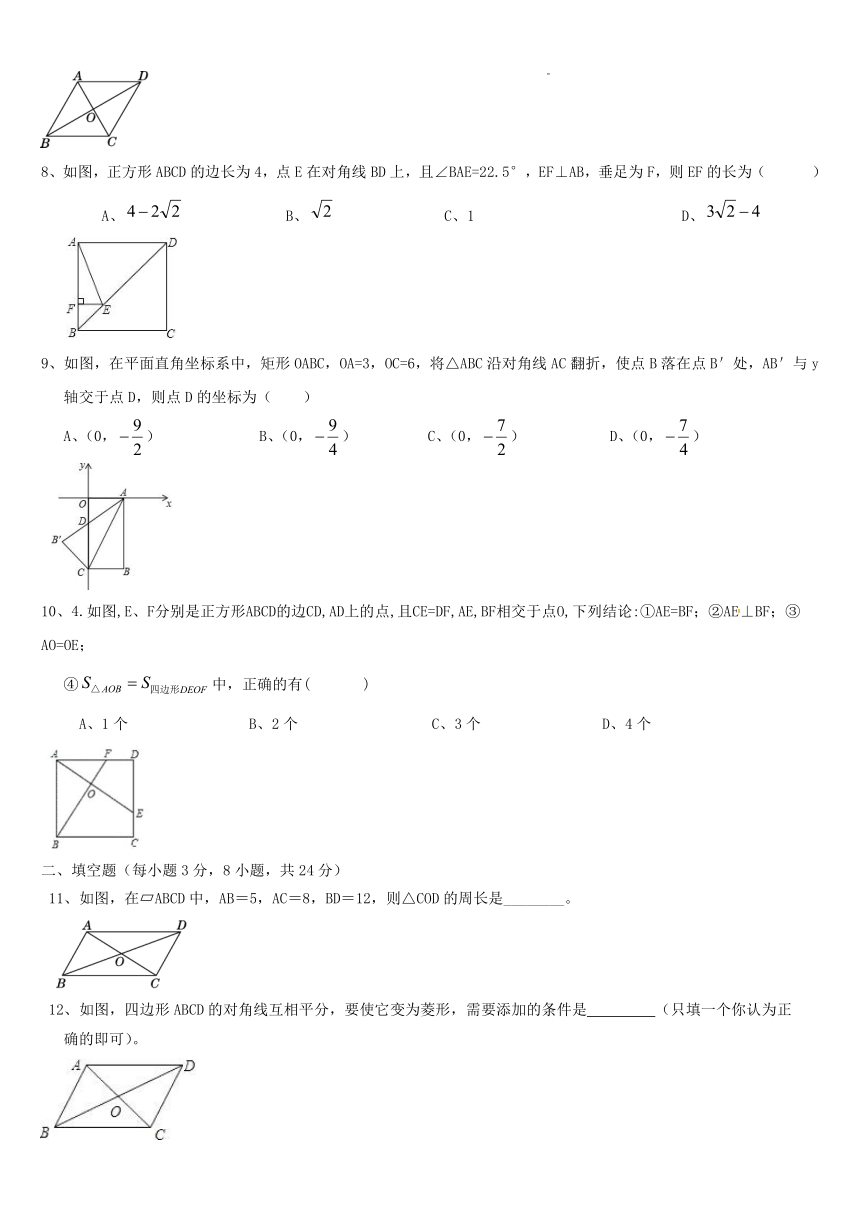
1、依据所标数据,下列一定为平行四边形的是( )
2、关于菱形的性质,以下说法不正确的是( )
四条边相等 B、对角线相等 C、对角线互相垂直 D、是轴对称图形
3、如图,在平行四边形ABCD中,延长AB到点E,使BE=AB,连接DE交BC于点F,则下列结论不一定成立的是( )
A、∠E=∠CDF B、BE=CD C、∠ADE=∠BFE D、BE=2CF
4、如图,在菱形ABCD中,AB的垂直平分线EF交对角线AC于点F,垂足为点E,连接DF,若∠CDF=24°,则∠DAB等于( )
A、100° B、104° C、105° D、110°
5、如图,将正方形OABC放在平面直角坐标系中,O是原点,若点A的坐标为(1,),则点C坐标为( )
A、( ,1) B、(-1, ) C、(-,1) D、(-,-1)
6、如图,在正方形ABCD外侧,作等边三角形ADE,AC,BE相交于点F,则∠BFC为( )
A、75° B、60° C、55° D、45°
7、如图,已知在菱形ABCD中,对角线AC与BD交于点O,∠BAD=120°,AC=4,则该菱形的面积是( )
A、 B、16 C、 D、8
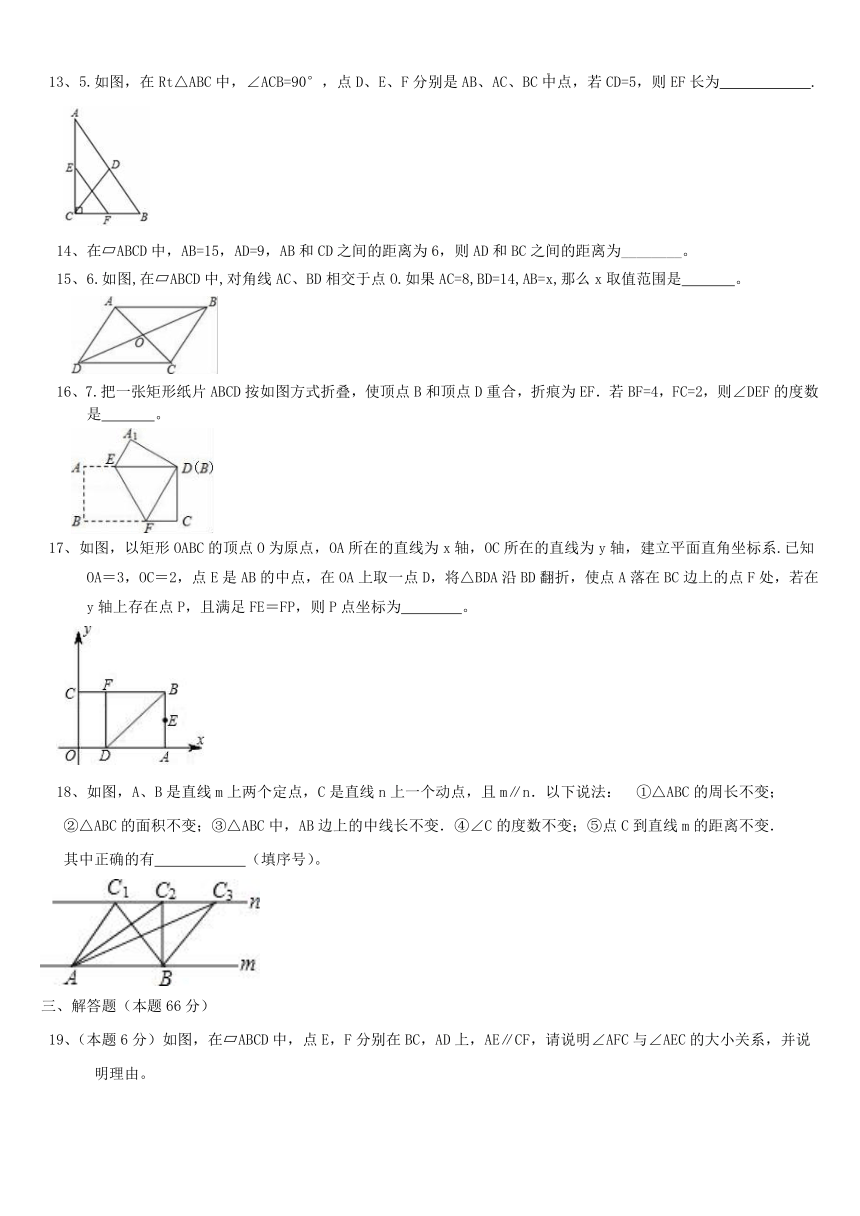
8、如图,正方形ABCD的边长为4,点E在对角线BD上,且∠BAE=22.5°,EF⊥AB,垂足为F,则EF的长为( )
A、 B、 C、1 D、
如图,在平面直角坐标系中,矩形OABC,OA=3,OC=6,将△ABC沿对角线AC翻折,使点B落在点B'处,AB'与y
轴交于点D,则点D的坐标为( )
A、(0,) B、(0,) C、(0,) D、(0,)
如图,E、F分别是正方形ABCD的边CD,AD上的点,且CE=DF,AE,BF相交于点O,下列结论:①AE=BF;②AE⊥BF;③AO=OE;
④中,正确的有( )
A、1个 B、2个 C、3个 D、4个
填空题(每小题3分,8小题,共24分)
11、如图,在 ABCD中,AB=5,AC=8,BD=12,则△COD的周长是________。
12、如图,四边形ABCD的对角线互相平分,要使它变为菱形,需要添加的条件是 (只填一个你认为正
确的即可)。
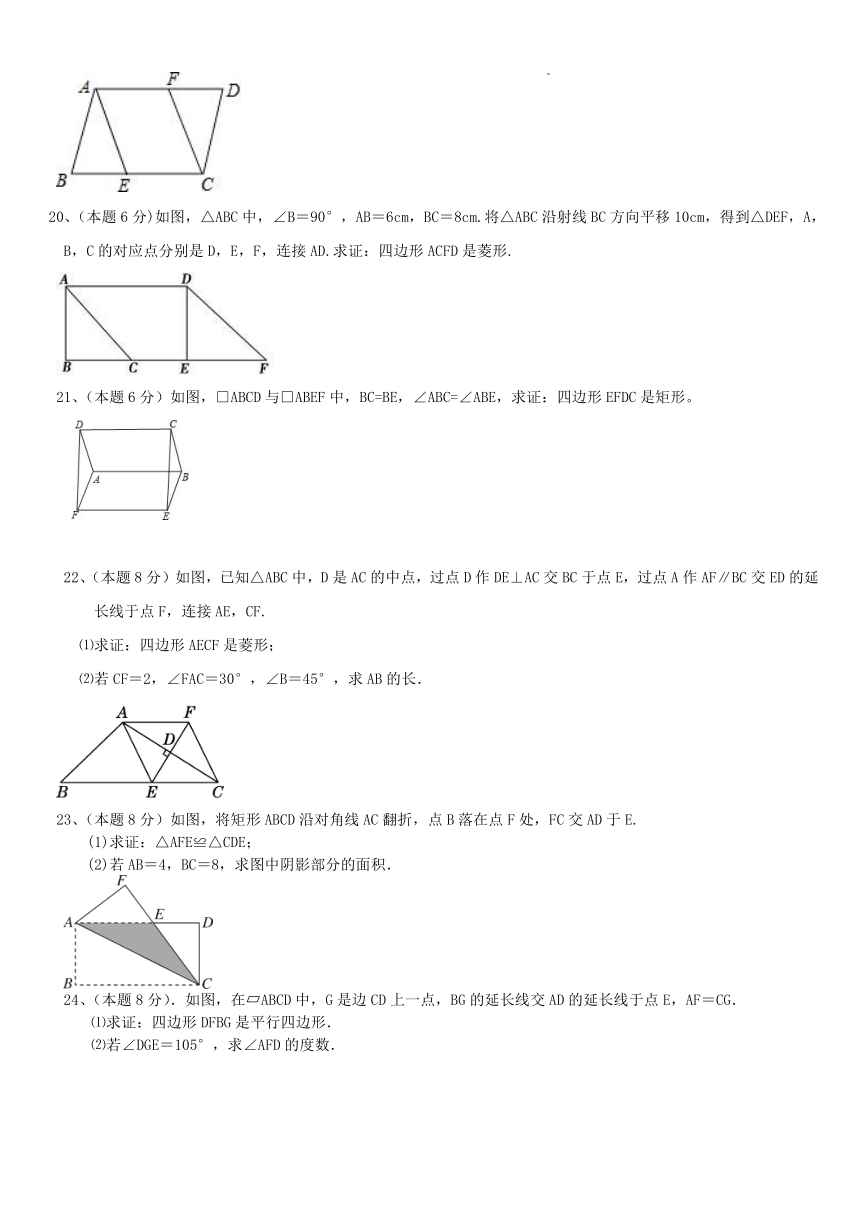
13、如图,在Rt△ABC中,∠ACB=90°,点D、E、F分别是AB、AC、BC中点,若CD=5,则EF长为 .
14、在 ABCD中,AB=15,AD=9,AB和CD之间的距离为6,则AD和BC之间的距离为________。
15、如图,在 ABCD中,对角线AC、BD相交于点O.如果AC=8,BD=14,AB=x,那么x取值范围是 。
16、把一张矩形纸片ABCD按如图方式折叠,使顶点B和顶点D重合,折痕为EF.若BF=4,FC=2,则∠DEF的度数
是 。
17、如图,以矩形OABC的顶点O为原点,OA所在的直线为x轴,OC所在的直线为y轴,建立平面直角坐标系.已知
OA=3,OC=2,点E是AB的中点,在OA上取一点D,将△BDA沿BD翻折,使点A落在BC边上的点F处,若在
y轴上存在点P,且满足FE=FP,则P点坐标为 。
18、如图,A、B是直线m上两个定点,C是直线n上一个动点,且m∥n.以下说法: ①△ABC的周长不变;
②△ABC的面积不变;③△ABC中,AB边上的中线长不变.④∠C的度数不变;⑤点C到直线m的距离不变.
其中正确的有 (填序号)。
解答题(本题66分)
19、(本题6分)如图,在 ABCD中,点E,F分别在BC,AD上,AE∥CF,请说明∠AFC与∠AEC的大小关系,并说
明理由。
20、(本题6分)如图,△ABC中,∠B=90°,AB=6cm,BC=8cm.将△ABC沿射线BC方向平移10cm,得到△DEF,A,
B,C的对应点分别是D,E,F,连接AD.求证:四边形ACFD是菱形.
21、(本题6分)如图,□ABCD与□ABEF中,BC=BE,∠ABC=∠ABE,求证:四边形EFDC是矩形。
22、(本题8分)如图,已知△ABC中,D是AC的中点,过点D作DE⊥AC交BC于点E,过点A作AF∥BC交ED的延
长线于点F,连接AE,CF.
⑴求证:四边形AECF是菱形;
⑵若CF=2,∠FAC=30°,∠B=45°,求AB的长.
23、(本题8分)如图,将矩形ABCD沿对角线AC翻折,点B落在点F处,FC交AD于E.
(1)求证:△AFE≌△CDE;
(2)若AB=4,BC=8,求图中阴影部分的面积.
24、(本题8分).如图,在 ABCD中,G是边CD上一点,BG的延长线交AD的延长线于点E,AF=CG.
⑴求证:四边形DFBG是平行四边形.
⑵若∠DGE=105°,求∠AFD的度数.
( 本题12分)如图,在Rt△ABC中,∠ACB=90°,过点C的直线MN∥AB,D为AB边上一点,过点D作DE⊥BC,交直线MN
于E,垂足为F,连接CD、BE.
⑴求证:CE=AD;
⑵当D在AB中点时,四边形BECD是什么特殊四边形?说明你的理由;
⑶若D为AB中点,则当∠A的大小满足什么条件时,四边形BECD是正方形?请说明你的理由.
(本题12分)在 ABCD中,AB≠AD,对角线AC,BD交于点O,AC=10,BD=16.点M,N在对角线BD上,点M从
点B出发以每秒1个单位长度的速度向点D运动,到达点D时停止运动,同时点N从点D出发,运动至点B后立
即返回,点M停止运动的同时,点N也停止运动,设运动时间为t秒(t>0).
(1)若点N的速度为每秒1个单位长度,
①如图,当0<t<8时,求证:四边形AMCN是平行四边形;
②点M,N运动的过程中,四边形AMCN可能出现的形状是________.
A、矩形 B、菱形 C、正方形
(2)若点N的速度为每秒2个单位长度,运动过程中,t为何值时,四边形AMCN是平行四边形?
参考答案:
选择题
D;2、B;3、D、4、B;5、C;6、 B ;7、A;8、A;9、B;10、C
填空题
11、15、12、AC⊥BD;13、5;14、10;15、;16、60°;17、(0,0)(0,4); 18、②⑤;
解答题
19、解:∠AFC=∠AEC, 理由如下:
∵平行四边形ABCD中,BC∥AD,
又AE∥CF,
∴四边形AECF为平行四边形,
∴∠AEC=∠AFC
20、证明:由平移变换的性质得:CF=AD=10cm,DF=AC,
∵∠B=90°,AB=6,BC=8,
∴,
∴AC=DF=AD=CF=10,
∴四边形ACFD是菱形.
21、∵在□ABCD与□ABEF中,AB∥CD,AB=CD,AB∥EF,AB=EF,
∴CD∥EF,CD=EF,
∴四边形EFDC是平行四边形,
∵BC=BE,∠ABC=∠ABE,
∴AB⊥CE,
∴CD⊥CE,
∴∠DCE=90°,
∴四边形EFDC是矩形。
22、(1)证明:在△ABC中,点D是AC的中点,
∴AD=DC.
∵AF∥BC,
∴∠FAD=∠ECD,∠AFD=∠CED.
∴△AFD≌△CED(AAS).
∴AF=EC.
又∵AF∥EC,
∴四边形AECF是平行四边形.
又∵EF⊥AC,
∴平行四边形AECF是菱形.
(2)解:如图,过点A作AG⊥BC于点G.
由(1)知四边形AECF是菱形,又CF=2,∠FAC=30°,
∴AE=CF=2,∠FAE=2∠FAC=60°.
∵AF∥BC,
∴∠AEB=∠FAE=60°.
∴∠GAE=30°.
∴GE=AE=1.
∴AG==.
∵∠B=45°,
∴AG=BG=.
∴AB==.
(1)证明:∵四边形ABCD是矩形,
∴AB=CD,∠B=∠D=90°
∵将矩形ABCD沿对角线AC翻折,点B落在点F处,
∴∠F=∠B,AB=AF,
∴AF=CD,∠F=∠D
在△AFE与△CDE中,∴△AFE≌△CDE.
(2)解:∵AB=4,BC=8,
∴CF=AD=8,AF=CD=AB=4.
∵△AFE≌△CDE,
∴EF=DE.
在Rt△CED中,由勾股定理得DE2+CD2=CE2,即DE2+42=(8-DE)2,
∴DE=3,
∴AE=8-3=5,
∴S阴影=×4×5=10.
24、⑴证明:在 ABCD中,∠A=∠C,AD=CB,AB=CD,
又∵AF=CG,
∴△ADF≌△CBG(SAS),且AB-AF=CD-CG.
∴DF=BG,BF=DG.
∴四边形DFBG是平行四边形.
⑵解:∵△ADF≌△CBG,
∴∠AFD=∠BGC=∠DGE=105°.
⑴证明:∵DE⊥BC,
∴∠DFB=90°,
∵∠ACB=90°,
∴∠ACB=∠DFB,
∴AC∥DE,
∵MN∥AB,即CE∥AD,
∴四边形ADEC是平行四边形,
∴CE=AD;
⑵解:四边形BECD是菱形,理由是:
∵D为AB中点,
∴AD=BD,
∵CE=AD,
∴BD=CE,
∵BD∥CE,
∴四边形BECD是平行四边形,
∵∠ACB=90°,D为AB中点,
∴CD=BD,
∴ 四边形BECD是菱形;
⑶解:当∠A=45°时,四边形BECD是正方形,理由是:
∵∠ACB=90°,∠A=45°,
∴∠ABC=∠A=45°,
∴AC=BC,
∵D为BA中点,
∴CD⊥AB,
∴∠CDB=90°,
∵四边形BECD是菱形,
∴菱形BECD是正方形,
即当∠A=45°时,四边形BECD是正方形.
26、(1)①证明:当0<t<8时,根据题意,得BM=DN=t.
∵四边形ABCD是平行四边形,
∴OA=OC,OB=OD.
∴OB-BM=OD-DN.
∴OM=ON.
∴四边形AMCN是平行四边形.
②A
(2)解:若点N的速度为每秒2个单位长度,则0当8若四边形AMCN是平行四边形,则OM=ON且点M,N在点O的两侧,
当0当4当8解得t=;
当12综上,当t=时,四边形AMCN是平行四边形.
(北京)股份有限公司
选择题(每小题3分,10小题,共30分)
1、依据所标数据,下列一定为平行四边形的是( )
2、关于菱形的性质,以下说法不正确的是( )
四条边相等 B、对角线相等 C、对角线互相垂直 D、是轴对称图形
3、如图,在平行四边形ABCD中,延长AB到点E,使BE=AB,连接DE交BC于点F,则下列结论不一定成立的是( )
A、∠E=∠CDF B、BE=CD C、∠ADE=∠BFE D、BE=2CF
4、如图,在菱形ABCD中,AB的垂直平分线EF交对角线AC于点F,垂足为点E,连接DF,若∠CDF=24°,则∠DAB等于( )
A、100° B、104° C、105° D、110°
5、如图,将正方形OABC放在平面直角坐标系中,O是原点,若点A的坐标为(1,),则点C坐标为( )
A、( ,1) B、(-1, ) C、(-,1) D、(-,-1)
6、如图,在正方形ABCD外侧,作等边三角形ADE,AC,BE相交于点F,则∠BFC为( )
A、75° B、60° C、55° D、45°
7、如图,已知在菱形ABCD中,对角线AC与BD交于点O,∠BAD=120°,AC=4,则该菱形的面积是( )
A、 B、16 C、 D、8
8、如图,正方形ABCD的边长为4,点E在对角线BD上,且∠BAE=22.5°,EF⊥AB,垂足为F,则EF的长为( )
A、 B、 C、1 D、
如图,在平面直角坐标系中,矩形OABC,OA=3,OC=6,将△ABC沿对角线AC翻折,使点B落在点B'处,AB'与y
轴交于点D,则点D的坐标为( )
A、(0,) B、(0,) C、(0,) D、(0,)
如图,E、F分别是正方形ABCD的边CD,AD上的点,且CE=DF,AE,BF相交于点O,下列结论:①AE=BF;②AE⊥BF;③AO=OE;
④中,正确的有( )
A、1个 B、2个 C、3个 D、4个
填空题(每小题3分,8小题,共24分)
11、如图,在 ABCD中,AB=5,AC=8,BD=12,则△COD的周长是________。
12、如图,四边形ABCD的对角线互相平分,要使它变为菱形,需要添加的条件是 (只填一个你认为正
确的即可)。
13、如图,在Rt△ABC中,∠ACB=90°,点D、E、F分别是AB、AC、BC中点,若CD=5,则EF长为 .
14、在 ABCD中,AB=15,AD=9,AB和CD之间的距离为6,则AD和BC之间的距离为________。
15、如图,在 ABCD中,对角线AC、BD相交于点O.如果AC=8,BD=14,AB=x,那么x取值范围是 。
16、把一张矩形纸片ABCD按如图方式折叠,使顶点B和顶点D重合,折痕为EF.若BF=4,FC=2,则∠DEF的度数
是 。
17、如图,以矩形OABC的顶点O为原点,OA所在的直线为x轴,OC所在的直线为y轴,建立平面直角坐标系.已知
OA=3,OC=2,点E是AB的中点,在OA上取一点D,将△BDA沿BD翻折,使点A落在BC边上的点F处,若在
y轴上存在点P,且满足FE=FP,则P点坐标为 。
18、如图,A、B是直线m上两个定点,C是直线n上一个动点,且m∥n.以下说法: ①△ABC的周长不变;
②△ABC的面积不变;③△ABC中,AB边上的中线长不变.④∠C的度数不变;⑤点C到直线m的距离不变.
其中正确的有 (填序号)。
解答题(本题66分)
19、(本题6分)如图,在 ABCD中,点E,F分别在BC,AD上,AE∥CF,请说明∠AFC与∠AEC的大小关系,并说
明理由。
20、(本题6分)如图,△ABC中,∠B=90°,AB=6cm,BC=8cm.将△ABC沿射线BC方向平移10cm,得到△DEF,A,
B,C的对应点分别是D,E,F,连接AD.求证:四边形ACFD是菱形.
21、(本题6分)如图,□ABCD与□ABEF中,BC=BE,∠ABC=∠ABE,求证:四边形EFDC是矩形。
22、(本题8分)如图,已知△ABC中,D是AC的中点,过点D作DE⊥AC交BC于点E,过点A作AF∥BC交ED的延
长线于点F,连接AE,CF.
⑴求证:四边形AECF是菱形;
⑵若CF=2,∠FAC=30°,∠B=45°,求AB的长.
23、(本题8分)如图,将矩形ABCD沿对角线AC翻折,点B落在点F处,FC交AD于E.
(1)求证:△AFE≌△CDE;
(2)若AB=4,BC=8,求图中阴影部分的面积.
24、(本题8分).如图,在 ABCD中,G是边CD上一点,BG的延长线交AD的延长线于点E,AF=CG.
⑴求证:四边形DFBG是平行四边形.
⑵若∠DGE=105°,求∠AFD的度数.
( 本题12分)如图,在Rt△ABC中,∠ACB=90°,过点C的直线MN∥AB,D为AB边上一点,过点D作DE⊥BC,交直线MN
于E,垂足为F,连接CD、BE.
⑴求证:CE=AD;
⑵当D在AB中点时,四边形BECD是什么特殊四边形?说明你的理由;
⑶若D为AB中点,则当∠A的大小满足什么条件时,四边形BECD是正方形?请说明你的理由.
(本题12分)在 ABCD中,AB≠AD,对角线AC,BD交于点O,AC=10,BD=16.点M,N在对角线BD上,点M从
点B出发以每秒1个单位长度的速度向点D运动,到达点D时停止运动,同时点N从点D出发,运动至点B后立
即返回,点M停止运动的同时,点N也停止运动,设运动时间为t秒(t>0).
(1)若点N的速度为每秒1个单位长度,
①如图,当0<t<8时,求证:四边形AMCN是平行四边形;
②点M,N运动的过程中,四边形AMCN可能出现的形状是________.
A、矩形 B、菱形 C、正方形
(2)若点N的速度为每秒2个单位长度,运动过程中,t为何值时,四边形AMCN是平行四边形?
参考答案:
选择题
D;2、B;3、D、4、B;5、C;6、 B ;7、A;8、A;9、B;10、C
填空题
11、15、12、AC⊥BD;13、5;14、10;15、;16、60°;17、(0,0)(0,4); 18、②⑤;
解答题
19、解:∠AFC=∠AEC, 理由如下:
∵平行四边形ABCD中,BC∥AD,
又AE∥CF,
∴四边形AECF为平行四边形,
∴∠AEC=∠AFC
20、证明:由平移变换的性质得:CF=AD=10cm,DF=AC,
∵∠B=90°,AB=6,BC=8,
∴,
∴AC=DF=AD=CF=10,
∴四边形ACFD是菱形.
21、∵在□ABCD与□ABEF中,AB∥CD,AB=CD,AB∥EF,AB=EF,
∴CD∥EF,CD=EF,
∴四边形EFDC是平行四边形,
∵BC=BE,∠ABC=∠ABE,
∴AB⊥CE,
∴CD⊥CE,
∴∠DCE=90°,
∴四边形EFDC是矩形。
22、(1)证明:在△ABC中,点D是AC的中点,
∴AD=DC.
∵AF∥BC,
∴∠FAD=∠ECD,∠AFD=∠CED.
∴△AFD≌△CED(AAS).
∴AF=EC.
又∵AF∥EC,
∴四边形AECF是平行四边形.
又∵EF⊥AC,
∴平行四边形AECF是菱形.
(2)解:如图,过点A作AG⊥BC于点G.
由(1)知四边形AECF是菱形,又CF=2,∠FAC=30°,
∴AE=CF=2,∠FAE=2∠FAC=60°.
∵AF∥BC,
∴∠AEB=∠FAE=60°.
∴∠GAE=30°.
∴GE=AE=1.
∴AG==.
∵∠B=45°,
∴AG=BG=.
∴AB==.
(1)证明:∵四边形ABCD是矩形,
∴AB=CD,∠B=∠D=90°
∵将矩形ABCD沿对角线AC翻折,点B落在点F处,
∴∠F=∠B,AB=AF,
∴AF=CD,∠F=∠D
在△AFE与△CDE中,∴△AFE≌△CDE.
(2)解:∵AB=4,BC=8,
∴CF=AD=8,AF=CD=AB=4.
∵△AFE≌△CDE,
∴EF=DE.
在Rt△CED中,由勾股定理得DE2+CD2=CE2,即DE2+42=(8-DE)2,
∴DE=3,
∴AE=8-3=5,
∴S阴影=×4×5=10.
24、⑴证明:在 ABCD中,∠A=∠C,AD=CB,AB=CD,
又∵AF=CG,
∴△ADF≌△CBG(SAS),且AB-AF=CD-CG.
∴DF=BG,BF=DG.
∴四边形DFBG是平行四边形.
⑵解:∵△ADF≌△CBG,
∴∠AFD=∠BGC=∠DGE=105°.
⑴证明:∵DE⊥BC,
∴∠DFB=90°,
∵∠ACB=90°,
∴∠ACB=∠DFB,
∴AC∥DE,
∵MN∥AB,即CE∥AD,
∴四边形ADEC是平行四边形,
∴CE=AD;
⑵解:四边形BECD是菱形,理由是:
∵D为AB中点,
∴AD=BD,
∵CE=AD,
∴BD=CE,
∵BD∥CE,
∴四边形BECD是平行四边形,
∵∠ACB=90°,D为AB中点,
∴CD=BD,
∴ 四边形BECD是菱形;
⑶解:当∠A=45°时,四边形BECD是正方形,理由是:
∵∠ACB=90°,∠A=45°,
∴∠ABC=∠A=45°,
∴AC=BC,
∵D为BA中点,
∴CD⊥AB,
∴∠CDB=90°,
∵四边形BECD是菱形,
∴菱形BECD是正方形,
即当∠A=45°时,四边形BECD是正方形.
26、(1)①证明:当0<t<8时,根据题意,得BM=DN=t.
∵四边形ABCD是平行四边形,
∴OA=OC,OB=OD.
∴OB-BM=OD-DN.
∴OM=ON.
∴四边形AMCN是平行四边形.
②A
(2)解:若点N的速度为每秒2个单位长度,则0
当0
当12
(北京)股份有限公司
