六、圆 单元练习卷 苏教版数学 五年级下册(含答案)
文档属性
| 名称 | 六、圆 单元练习卷 苏教版数学 五年级下册(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 244.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-04-16 13:31:48 | ||
图片预览




文档简介
六、圆 单元练习卷 苏教版数学 五年级下册
学校:___________姓名:___________班级:___________考号:___________
一、填空题
1.在同一个圆中,所有的半径都( ),所有的直径都( ),直径的长度是半径的( ),圆的位置由( )决定,圆的( )由半径决定。
2.一个半圆的直径是4分米,则这个半圆的周长是( )分米。
3.画一个周长是3.14厘米的圆,圆规两脚间的距离是( )厘米。
4.一个圆的周长是12.56厘米,这个圆的面积是多少?要求这个圆的面积,要先求出圆的( ),列式计算为( ),再求圆的面积,列式为( )。
5.一根75.36分米长的丝带正好可以给两张相同的圆形卡片包边,每张圆形卡片的面积是( )平方分米。
二、判断题
6.所有的直径(或半径)都相等。( )
7.大圆的圆周率大于小圆的圆周率。( )
8.长方形、圆形和等腰三角形都是轴对称图形。( )
9.一个圆,半径变为原来的2倍,周长和面积也都变为原来的2倍。( )
10.两个大小不同的圆,如果这两个圆的半径都增加3厘米,那么它们的周长增加的部分相比,大圆增加的长。( )
三、选择题
11.下面涂色部分是扇形的是( )。
A. B. C.
12.用3段一样长的铁丝,分别围成一个正三角形、一个正方形、一个圆,在围成的图形中,( )的面积最大。
A.圆 B.正方形 C.正三角形
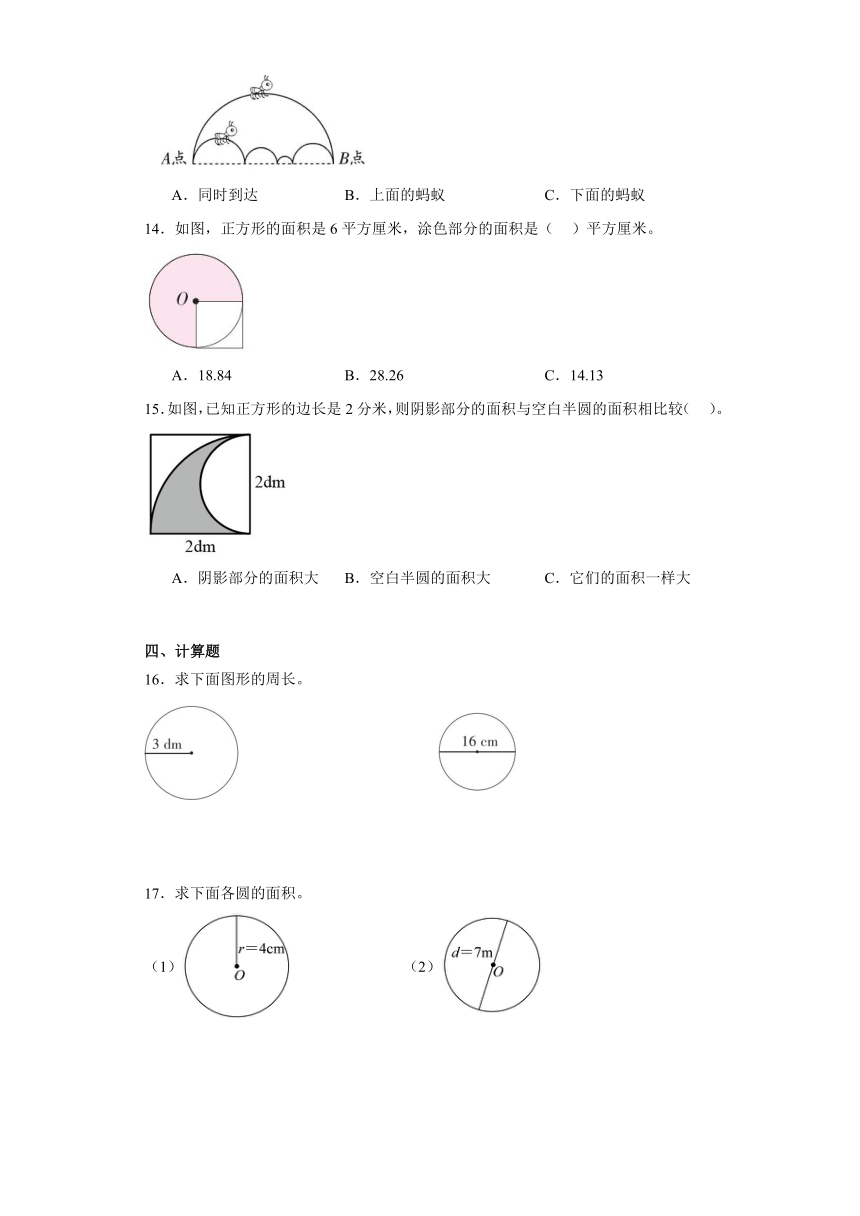
13.下雨了,小蚂蚁要从A点把食物运回B点,两只蚂蚁同时从A点出发,以同样的速度爬(路线如下图)。哪只蚂蚁先把食物运回B点?( )
A.同时到达 B.上面的蚂蚁 C.下面的蚂蚁
14.如图,正方形的面积是6平方厘米,涂色部分的面积是( )平方厘米。
A.18.84 B.28.26 C.14.13
15.如图,已知正方形的边长是2分米,则阴影部分的面积与空白半圆的面积相比较( )。
A.阴影部分的面积大 B.空白半圆的面积大 C.它们的面积一样大
四、计算题
16.求下面图形的周长。
17.求下面各圆的面积。
(1) (2)
五、作图题
18.一件环形玉佩的内圆直径是3厘米,外圆直径是5厘米,在方格图中按环形玉佩的尺寸画一个圆环。
六、解答题
19.一个铁环的直径是60厘米,从操场东端滚到西端转了90圈。另一个铁环的直径是40厘米,它从操场东端滚到西端要转多少圈?
20.沙子堆在地面上占地正好是圆形,量出它一周的长度是15.7米,那么直径是多少米?
21.用席子围成一个地面周长是18.84米的圆柱形粮囤.这个粮囤占地面积有多大?
22.求图中阴影部分的面积.(单位:厘米)
23.一位杂技演员在悬空的钢丝上骑独轮车。独轮车车轮的直径是45厘米,从钢丝的一端到另一端,车轮正好滚动40圈。这根悬空的钢丝长多少米?
24.一个圆形旱冰场的直径是30米,扩建后半径增加了5米。扩建后旱冰场的面积增加了多少平方米?
参考答案:
1. 相等 相等 2倍 圆心 大小
【详解】
在同一个圆中,所有的半径都相等,所有的直径都相等,直径的长度是半径的2倍,圆的位置由圆心决定,圆的大小由半径决定。
如图:
2.10.28
【分析】注意不要混淆圆的周长的一半和半圆的周长,根据半圆的周长=圆的周长的一半+直径,代入数据即可得解。
【详解】3.14×4÷2+4
=12.56÷2+4
=6.28+4
=10.28(分米)
则这个半圆的周长是10.28分米。
3.0.5
【分析】画圆时,圆规两脚之间的距离是圆的半径。根据圆的周长=2×π×半径可知,半径=周长÷π÷2即可求出半径,也即是求出圆规两脚间的距离。
【详解】由分析可知:3.14÷3.14÷2
=1÷2
=0.5(厘米)
故圆规两脚间的距离是0.5厘米。
4. 半径 12.56÷3.14÷2=2(厘米) 3.14×22=12.56(平方厘米)
【分析】由题意知:圆的周长已知,利用求得圆的半径,再根据圆的面积公式,将数值代入即可求得圆的面积。据此解答。
【详解】
=
=2(厘米)
=(平方厘米)
要求这个圆的面积,要先求出圆的(半径),列式计算为(厘米),再求圆的面积,列式为(平方厘米)。
【点睛】
5.113.04
【分析】
先用75.36÷2即可求出每张圆形卡片的周长,然后根据圆的周长公式:C=2πr,用75.36÷2÷2÷3.14即可求出圆的半径,再根据圆的面积公式:S=πr2,代入数据即可求出每张圆形卡片的面积。
【详解】75.36÷2÷2÷3.14=6(分米)
3.14×62
=3.14×36
=113.04(平方分米)
每张圆形卡片的面积是113.04平方分米。
6.×
【分析】在同圆或等圆中,所有的直径(或半径)都相等;如果不限定是什么样的圆,那么这句话是错的,据此解答。
【详解】在同圆或等圆中,所有的直径(或半径)都相等;在不等的圆中,所有的直径(或半径)都不相等,因此这句话是错的。
故答案为:×
7.×
【分析】根据圆周率的含义:圆的周长和它直径的比值,叫做圆周率;圆周率用“π”表示,π是一个无限不循环小数;进而判断即可。
【详解】根据分析可知,圆周率是一个定值,不存在大圆的圆周率大于小圆的圆周率。
原题干说法错误。
故答案为:×
【点睛】明确圆周率的意义是解答本题的关键。
8.√
【分析】一个图形沿一条直线对折后,折痕两旁的部分能够完全重合,这样的图形就是轴对称图形,这条直线就是对称轴。
【详解】长方形有2条对称轴,是轴对称图形;
圆有无数条对称轴,是轴对称图形;
等腰三角形有1条对称轴,是轴对称图形;
所以,长方形、圆形和等腰三角形都是轴对称图形。
原题说法正确。
故答案为:√
【点睛】掌握轴对称图形的意义及特点,判断是不是轴对称图形的关键是找出对称轴,看图形沿对称轴对折后两部分能否完全重合。
9.×
【分析】设圆的半径是1,半径变为原来的2倍,则扩大后圆的半径为1×2=2,根据圆的周长公式:周长=π×半径×2,分别求出原来圆的周长和扩大后圆的周长,再用扩大后圆的周长除以扩大前圆的周长,求出周长变为原来的多少倍;圆的面积公式:面积=π×半径2,分别求出扩大前和扩大后圆的面积,再用扩大后圆的面积除以扩大前圆的面积,即可求出面积变为原来的多少倍,据此解答。
【详解】设圆的半径是1,则扩大后圆的半径为1×2=2。
(3.14×2×2)÷(3.14×1×2)
=(6.28×2)÷(3.14×2)
=12.56÷6.28
=2
(3.14×22)÷(3.14×12)
=(3.14×4)÷(3.14×1)
=12.56÷3.14
=4
一个圆,半径变为原来的2倍,周长变为原来的2倍,面积变为原来的4倍。
原题干说法错误。
故答案为:×
10.×
【分析】圆的周长=2πr,半径增加3cm后,周长为:2π(r+3)=2πr+6π,由此可得,半径增加3cm,则它们的周长就增加了6π厘米,由此即可判断。
【详解】圆的周长=2πr,半径增加3cm,则周长为:2π(r+3)=2πr+6π,
所以,半径增加3cm,则它们的周长都是增加6π厘米,增加的一样多。原题说法错误。
故答案为:×
【点睛】此题考查圆的周长公式的灵活应用,半径增加几,周长就增加几个2π的值。
11.B
【分析】
根据扇形的定义:在一个圆中,一条弧和经过这条弧两端的两条半径所围成的图形叫做扇形,据此判断即可。
【详解】在一个圆中,一条弧和经过这条弧两端的两条半径所围成的图形叫做扇形。
A.连接弧两端的两条线段不是圆的半径,故A选项不符合题意。
B.连接弧两端的线段是圆的半径,故B符合题意。
C.连接弧两端的两条线段不是圆的半径,故C选项不符合题意。
故答案为:B
12.A
【分析】根据题意,用同样长的铁丝围成正三角形、正方形和圆,那么正三角形、正方形和圆的周长都等于铁丝的长度,可以设铁丝长18.84米;
A.根据圆的周长公式C=2πr可知,r=C÷π÷2,由此求出圆的半径;再根据圆的面积公式S=πr2,求出圆的面积;
B.根据正方形的周长=边长×4可知,正方形的边长=周长÷4;再根据正方形的面积=边长×边长,求出正方形的面积;
C.正三角形的3条边相等,则正三角形的边长=周长÷3;又因为正三角形的高在直角三角形中,根据“直角三角形中斜边最长”可知,正三角形的高要小于边长;根据三角形的面积=底×高÷2,可以求出三角形面积的范围;
最后比较三个图形的面积大小,得出哪个图形的面积最大。
【详解】设3段铁丝的长度都是18.84米。
A.圆的半径:18.84÷3.14÷2=3(米)
圆的面积:3.14×3×3=28.26(平方米)
B.正方形的边长:18.84÷4=4.71(米)
正方形的面积:4.71×4.71=22.1841(平方米)
C.正三角形的边长:18.84÷3=6.28(米)
正三角形的高小于边长6.28米;
则三角形的面积小于:6.28×6.28÷2=19.7192(平方米)
28.26>22.1841>19.7192
圆的面积>正方形的面积>正三角形的面积
所以,在围成的图形中,圆的面积最大。
故答案为:A
13.A
【分析】根据图可知,上面蚂蚁走了一个大半圆的圆弧,下面的小蚂蚁走了4个半圆弧的长度,可以设下面小蚂蚁走的4个半圆的直径分别是d1,d2,d3,d4,根据圆的周长公式:C=πd,分别求出两只蚂蚁走的路程,再进行比较即可。
【详解】设四个小半圆的直径分别是d1,d2,d3,d4。
上面蚂蚁走的长度:π×(d1+d2+d3+d4)÷2
下面蚂蚁走的长度:π×d1÷2+π×d2÷2+π×d3÷2+π×d4÷2=π×(d1+d2+d3+d4)÷2
由此即可知道两只蚂蚁走的长度一样,所以同时把食物运回B点。
故答案为:A
【点睛】本题主要考查圆的周长公式,要注意当多个小圆的直径和跟大圆的直径相等时,两个圆的周长相等。
14.C
【分析】
观察图形可知,涂色部分的面积=圆的面积-圆的面积=圆的面积;
从图中可知,正方形的边长等于圆的半径,根据正方形的面积公式S=a2可知,正方形的面积正好是r2,把r2的值代入圆的面积公式S=πr2中计算,即可求出圆的面积,再乘,即是涂色部分的面积。
【详解】3.14×6×
=18.84×
=14.13(平方厘米)
涂色部分的面积是14.13平方厘米。
故答案为:C
15.C
【分析】根据图示,分别计算阴影部分的面积和空白部分的面积,然后比较解答即可。
【详解】阴影部分面积:
3.14×22÷4
=3.14×4÷4
=12.56÷4
=3.14(平方分米)
空白部分的面积:
3.14×(2÷2)2
=3.14×12
=3.14×1
=3.14(平方分米)
3.14=3.14
所以阴影部分面积与空白半圆的面积一样大。
故答案为:C
【点睛】本题考查了圆面积公式的灵活运用知识,结合题意分析解答即可。
16.18.84dm;50.24cm
【分析】
根据圆的周长=圆周率×直径=2×圆周率×半径,列式计算即可。
【详解】
2×3.14×3=18.84(dm)
3.14×16=50.24(cm)
17.(1)50.24cm2;(2)38.465m2
【分析】
根据圆的面积=πr2,代入数据解答即可。
【详解】
(1)3.14×42
=3.14×16
=50.24(cm2)
圆的面积是50.24cm2。
(2)3.14×(7÷2)2
=3.14×12.25
=38.465(m2)
圆的面积是38.465m2。
18.见详解
【分析】画圆的步骤:把圆规的两脚分开,定好两脚的距离,即半径;把有针尖的一只脚固定在一点上,即圆心;把装有铅笔尖的一只脚旋转一周,就画出一个圆。
直径÷2=半径,据此确定圆心和半径,根据画圆的方法,分别画出直径3厘米和直径5厘米的两个同心圆即可。
【详解】3÷2=1.5(厘米)
5÷2=2.5(厘米)
19.135圈
【分析】根据题意,直径是60厘米的铁环周长×90求出操场东端到西端的距离,再除以直径是40厘米的铁环周长即可。
【详解】3.14×60×90÷(3.14×40)
=16956÷125.6
=135(圈)
答:它从操场东端滚到西端要转135圈。
【点睛】此题主要考查了圆的周长的实际应用,明确圆的周长C=πd。
20.5米
【分析】由圆的周长=πd,所以直径d=周长÷π。
【详解】15.7÷3.14=5(米)
答:直径是5米。
【点睛】此题主要考查的是圆的周长公式的灵活应用。
21.28.26平方米
【详解】分析:根据圆的周长公式C=2πr得出r=C÷π÷2,由此求出围成的圆柱的底面半径,再根据圆的面积公式S=πr2求出这个粮囤占地面积.
解答:解:18.84÷3.14÷2=3(米),
3.14×32
=3.14×9
=28.26(平方米)
答:这个粮囤占地面积是28.26平方米.
点评:本题主要是灵活利用圆的周长公式C=2πr和圆的面积公式S=πr2解决问题.
考点:圆、圆环的面积.
22.25平方厘米
【详解】分析:如图,右边的阴影部分可以平移到左边,与左边的阴影部分组成一个三角形,不难得出阴影部分的面积等于这个直角边长是10厘米的三角形的面积的一半,据此即可解答问题.
解答:解:10×10÷2÷2=25(平方厘米)
答:阴影部分的面积是25平方厘米.
点评:此题考查了组合图形的面积的计算方法,关键是明确这个图形是哪几个图形的面积之和或差.
考点:组合图形的面积.
23.56.52米
【分析】钢丝长就是车轮滚动40圈的长度,也就是车轮的周长的40倍,车轮的直径已知,代入圆的周长公式计算即可,计算过程中注意单位的换算。
【详解】由题意知:
3.14×45×40
=141.3×40
=5652(厘米)
5652厘米=56.52米
答:这根悬空的钢丝长56.52米。
24.549.5平方米
【分析】根据题意可知,扩建后半径增加了5米,求面积增加了多少平方米,也就是求这个环形的面积,已知内圆直径,首先求出内圆半径,根据环形面积=外圆面积﹣内圆面积,由此列式解答。
【详解】内圆半径:
30÷2=15(米)
外圆半径:15+5=20(米)
增加的面积:
3.14×(202﹣152)
=3.14×(400﹣225)
=3.14×175
=549.5(平方米)
答:扩建后旱冰场的面积增加了549.5平方米。
【点睛】此题属于环形面积计算,根据环形面积公式:环形面积=外圆面积﹣内圆面积,或环形面积=3.14×(外圆半径的平方﹣内圆半径的平方);列式解答。
学校:___________姓名:___________班级:___________考号:___________
一、填空题
1.在同一个圆中,所有的半径都( ),所有的直径都( ),直径的长度是半径的( ),圆的位置由( )决定,圆的( )由半径决定。
2.一个半圆的直径是4分米,则这个半圆的周长是( )分米。
3.画一个周长是3.14厘米的圆,圆规两脚间的距离是( )厘米。
4.一个圆的周长是12.56厘米,这个圆的面积是多少?要求这个圆的面积,要先求出圆的( ),列式计算为( ),再求圆的面积,列式为( )。
5.一根75.36分米长的丝带正好可以给两张相同的圆形卡片包边,每张圆形卡片的面积是( )平方分米。
二、判断题
6.所有的直径(或半径)都相等。( )
7.大圆的圆周率大于小圆的圆周率。( )
8.长方形、圆形和等腰三角形都是轴对称图形。( )
9.一个圆,半径变为原来的2倍,周长和面积也都变为原来的2倍。( )
10.两个大小不同的圆,如果这两个圆的半径都增加3厘米,那么它们的周长增加的部分相比,大圆增加的长。( )
三、选择题
11.下面涂色部分是扇形的是( )。
A. B. C.
12.用3段一样长的铁丝,分别围成一个正三角形、一个正方形、一个圆,在围成的图形中,( )的面积最大。
A.圆 B.正方形 C.正三角形
13.下雨了,小蚂蚁要从A点把食物运回B点,两只蚂蚁同时从A点出发,以同样的速度爬(路线如下图)。哪只蚂蚁先把食物运回B点?( )
A.同时到达 B.上面的蚂蚁 C.下面的蚂蚁
14.如图,正方形的面积是6平方厘米,涂色部分的面积是( )平方厘米。
A.18.84 B.28.26 C.14.13
15.如图,已知正方形的边长是2分米,则阴影部分的面积与空白半圆的面积相比较( )。
A.阴影部分的面积大 B.空白半圆的面积大 C.它们的面积一样大
四、计算题
16.求下面图形的周长。
17.求下面各圆的面积。
(1) (2)
五、作图题
18.一件环形玉佩的内圆直径是3厘米,外圆直径是5厘米,在方格图中按环形玉佩的尺寸画一个圆环。
六、解答题
19.一个铁环的直径是60厘米,从操场东端滚到西端转了90圈。另一个铁环的直径是40厘米,它从操场东端滚到西端要转多少圈?
20.沙子堆在地面上占地正好是圆形,量出它一周的长度是15.7米,那么直径是多少米?
21.用席子围成一个地面周长是18.84米的圆柱形粮囤.这个粮囤占地面积有多大?
22.求图中阴影部分的面积.(单位:厘米)
23.一位杂技演员在悬空的钢丝上骑独轮车。独轮车车轮的直径是45厘米,从钢丝的一端到另一端,车轮正好滚动40圈。这根悬空的钢丝长多少米?
24.一个圆形旱冰场的直径是30米,扩建后半径增加了5米。扩建后旱冰场的面积增加了多少平方米?
参考答案:
1. 相等 相等 2倍 圆心 大小
【详解】
在同一个圆中,所有的半径都相等,所有的直径都相等,直径的长度是半径的2倍,圆的位置由圆心决定,圆的大小由半径决定。
如图:
2.10.28
【分析】注意不要混淆圆的周长的一半和半圆的周长,根据半圆的周长=圆的周长的一半+直径,代入数据即可得解。
【详解】3.14×4÷2+4
=12.56÷2+4
=6.28+4
=10.28(分米)
则这个半圆的周长是10.28分米。
3.0.5
【分析】画圆时,圆规两脚之间的距离是圆的半径。根据圆的周长=2×π×半径可知,半径=周长÷π÷2即可求出半径,也即是求出圆规两脚间的距离。
【详解】由分析可知:3.14÷3.14÷2
=1÷2
=0.5(厘米)
故圆规两脚间的距离是0.5厘米。
4. 半径 12.56÷3.14÷2=2(厘米) 3.14×22=12.56(平方厘米)
【分析】由题意知:圆的周长已知,利用求得圆的半径,再根据圆的面积公式,将数值代入即可求得圆的面积。据此解答。
【详解】
=
=2(厘米)
=(平方厘米)
要求这个圆的面积,要先求出圆的(半径),列式计算为(厘米),再求圆的面积,列式为(平方厘米)。
【点睛】
5.113.04
【分析】
先用75.36÷2即可求出每张圆形卡片的周长,然后根据圆的周长公式:C=2πr,用75.36÷2÷2÷3.14即可求出圆的半径,再根据圆的面积公式:S=πr2,代入数据即可求出每张圆形卡片的面积。
【详解】75.36÷2÷2÷3.14=6(分米)
3.14×62
=3.14×36
=113.04(平方分米)
每张圆形卡片的面积是113.04平方分米。
6.×
【分析】在同圆或等圆中,所有的直径(或半径)都相等;如果不限定是什么样的圆,那么这句话是错的,据此解答。
【详解】在同圆或等圆中,所有的直径(或半径)都相等;在不等的圆中,所有的直径(或半径)都不相等,因此这句话是错的。
故答案为:×
7.×
【分析】根据圆周率的含义:圆的周长和它直径的比值,叫做圆周率;圆周率用“π”表示,π是一个无限不循环小数;进而判断即可。
【详解】根据分析可知,圆周率是一个定值,不存在大圆的圆周率大于小圆的圆周率。
原题干说法错误。
故答案为:×
【点睛】明确圆周率的意义是解答本题的关键。
8.√
【分析】一个图形沿一条直线对折后,折痕两旁的部分能够完全重合,这样的图形就是轴对称图形,这条直线就是对称轴。
【详解】长方形有2条对称轴,是轴对称图形;
圆有无数条对称轴,是轴对称图形;
等腰三角形有1条对称轴,是轴对称图形;
所以,长方形、圆形和等腰三角形都是轴对称图形。
原题说法正确。
故答案为:√
【点睛】掌握轴对称图形的意义及特点,判断是不是轴对称图形的关键是找出对称轴,看图形沿对称轴对折后两部分能否完全重合。
9.×
【分析】设圆的半径是1,半径变为原来的2倍,则扩大后圆的半径为1×2=2,根据圆的周长公式:周长=π×半径×2,分别求出原来圆的周长和扩大后圆的周长,再用扩大后圆的周长除以扩大前圆的周长,求出周长变为原来的多少倍;圆的面积公式:面积=π×半径2,分别求出扩大前和扩大后圆的面积,再用扩大后圆的面积除以扩大前圆的面积,即可求出面积变为原来的多少倍,据此解答。
【详解】设圆的半径是1,则扩大后圆的半径为1×2=2。
(3.14×2×2)÷(3.14×1×2)
=(6.28×2)÷(3.14×2)
=12.56÷6.28
=2
(3.14×22)÷(3.14×12)
=(3.14×4)÷(3.14×1)
=12.56÷3.14
=4
一个圆,半径变为原来的2倍,周长变为原来的2倍,面积变为原来的4倍。
原题干说法错误。
故答案为:×
10.×
【分析】圆的周长=2πr,半径增加3cm后,周长为:2π(r+3)=2πr+6π,由此可得,半径增加3cm,则它们的周长就增加了6π厘米,由此即可判断。
【详解】圆的周长=2πr,半径增加3cm,则周长为:2π(r+3)=2πr+6π,
所以,半径增加3cm,则它们的周长都是增加6π厘米,增加的一样多。原题说法错误。
故答案为:×
【点睛】此题考查圆的周长公式的灵活应用,半径增加几,周长就增加几个2π的值。
11.B
【分析】
根据扇形的定义:在一个圆中,一条弧和经过这条弧两端的两条半径所围成的图形叫做扇形,据此判断即可。
【详解】在一个圆中,一条弧和经过这条弧两端的两条半径所围成的图形叫做扇形。
A.连接弧两端的两条线段不是圆的半径,故A选项不符合题意。
B.连接弧两端的线段是圆的半径,故B符合题意。
C.连接弧两端的两条线段不是圆的半径,故C选项不符合题意。
故答案为:B
12.A
【分析】根据题意,用同样长的铁丝围成正三角形、正方形和圆,那么正三角形、正方形和圆的周长都等于铁丝的长度,可以设铁丝长18.84米;
A.根据圆的周长公式C=2πr可知,r=C÷π÷2,由此求出圆的半径;再根据圆的面积公式S=πr2,求出圆的面积;
B.根据正方形的周长=边长×4可知,正方形的边长=周长÷4;再根据正方形的面积=边长×边长,求出正方形的面积;
C.正三角形的3条边相等,则正三角形的边长=周长÷3;又因为正三角形的高在直角三角形中,根据“直角三角形中斜边最长”可知,正三角形的高要小于边长;根据三角形的面积=底×高÷2,可以求出三角形面积的范围;
最后比较三个图形的面积大小,得出哪个图形的面积最大。
【详解】设3段铁丝的长度都是18.84米。
A.圆的半径:18.84÷3.14÷2=3(米)
圆的面积:3.14×3×3=28.26(平方米)
B.正方形的边长:18.84÷4=4.71(米)
正方形的面积:4.71×4.71=22.1841(平方米)
C.正三角形的边长:18.84÷3=6.28(米)
正三角形的高小于边长6.28米;
则三角形的面积小于:6.28×6.28÷2=19.7192(平方米)
28.26>22.1841>19.7192
圆的面积>正方形的面积>正三角形的面积
所以,在围成的图形中,圆的面积最大。
故答案为:A
13.A
【分析】根据图可知,上面蚂蚁走了一个大半圆的圆弧,下面的小蚂蚁走了4个半圆弧的长度,可以设下面小蚂蚁走的4个半圆的直径分别是d1,d2,d3,d4,根据圆的周长公式:C=πd,分别求出两只蚂蚁走的路程,再进行比较即可。
【详解】设四个小半圆的直径分别是d1,d2,d3,d4。
上面蚂蚁走的长度:π×(d1+d2+d3+d4)÷2
下面蚂蚁走的长度:π×d1÷2+π×d2÷2+π×d3÷2+π×d4÷2=π×(d1+d2+d3+d4)÷2
由此即可知道两只蚂蚁走的长度一样,所以同时把食物运回B点。
故答案为:A
【点睛】本题主要考查圆的周长公式,要注意当多个小圆的直径和跟大圆的直径相等时,两个圆的周长相等。
14.C
【分析】
观察图形可知,涂色部分的面积=圆的面积-圆的面积=圆的面积;
从图中可知,正方形的边长等于圆的半径,根据正方形的面积公式S=a2可知,正方形的面积正好是r2,把r2的值代入圆的面积公式S=πr2中计算,即可求出圆的面积,再乘,即是涂色部分的面积。
【详解】3.14×6×
=18.84×
=14.13(平方厘米)
涂色部分的面积是14.13平方厘米。
故答案为:C
15.C
【分析】根据图示,分别计算阴影部分的面积和空白部分的面积,然后比较解答即可。
【详解】阴影部分面积:
3.14×22÷4
=3.14×4÷4
=12.56÷4
=3.14(平方分米)
空白部分的面积:
3.14×(2÷2)2
=3.14×12
=3.14×1
=3.14(平方分米)
3.14=3.14
所以阴影部分面积与空白半圆的面积一样大。
故答案为:C
【点睛】本题考查了圆面积公式的灵活运用知识,结合题意分析解答即可。
16.18.84dm;50.24cm
【分析】
根据圆的周长=圆周率×直径=2×圆周率×半径,列式计算即可。
【详解】
2×3.14×3=18.84(dm)
3.14×16=50.24(cm)
17.(1)50.24cm2;(2)38.465m2
【分析】
根据圆的面积=πr2,代入数据解答即可。
【详解】
(1)3.14×42
=3.14×16
=50.24(cm2)
圆的面积是50.24cm2。
(2)3.14×(7÷2)2
=3.14×12.25
=38.465(m2)
圆的面积是38.465m2。
18.见详解
【分析】画圆的步骤:把圆规的两脚分开,定好两脚的距离,即半径;把有针尖的一只脚固定在一点上,即圆心;把装有铅笔尖的一只脚旋转一周,就画出一个圆。
直径÷2=半径,据此确定圆心和半径,根据画圆的方法,分别画出直径3厘米和直径5厘米的两个同心圆即可。
【详解】3÷2=1.5(厘米)
5÷2=2.5(厘米)
19.135圈
【分析】根据题意,直径是60厘米的铁环周长×90求出操场东端到西端的距离,再除以直径是40厘米的铁环周长即可。
【详解】3.14×60×90÷(3.14×40)
=16956÷125.6
=135(圈)
答:它从操场东端滚到西端要转135圈。
【点睛】此题主要考查了圆的周长的实际应用,明确圆的周长C=πd。
20.5米
【分析】由圆的周长=πd,所以直径d=周长÷π。
【详解】15.7÷3.14=5(米)
答:直径是5米。
【点睛】此题主要考查的是圆的周长公式的灵活应用。
21.28.26平方米
【详解】分析:根据圆的周长公式C=2πr得出r=C÷π÷2,由此求出围成的圆柱的底面半径,再根据圆的面积公式S=πr2求出这个粮囤占地面积.
解答:解:18.84÷3.14÷2=3(米),
3.14×32
=3.14×9
=28.26(平方米)
答:这个粮囤占地面积是28.26平方米.
点评:本题主要是灵活利用圆的周长公式C=2πr和圆的面积公式S=πr2解决问题.
考点:圆、圆环的面积.
22.25平方厘米
【详解】分析:如图,右边的阴影部分可以平移到左边,与左边的阴影部分组成一个三角形,不难得出阴影部分的面积等于这个直角边长是10厘米的三角形的面积的一半,据此即可解答问题.
解答:解:10×10÷2÷2=25(平方厘米)
答:阴影部分的面积是25平方厘米.
点评:此题考查了组合图形的面积的计算方法,关键是明确这个图形是哪几个图形的面积之和或差.
考点:组合图形的面积.
23.56.52米
【分析】钢丝长就是车轮滚动40圈的长度,也就是车轮的周长的40倍,车轮的直径已知,代入圆的周长公式计算即可,计算过程中注意单位的换算。
【详解】由题意知:
3.14×45×40
=141.3×40
=5652(厘米)
5652厘米=56.52米
答:这根悬空的钢丝长56.52米。
24.549.5平方米
【分析】根据题意可知,扩建后半径增加了5米,求面积增加了多少平方米,也就是求这个环形的面积,已知内圆直径,首先求出内圆半径,根据环形面积=外圆面积﹣内圆面积,由此列式解答。
【详解】内圆半径:
30÷2=15(米)
外圆半径:15+5=20(米)
增加的面积:
3.14×(202﹣152)
=3.14×(400﹣225)
=3.14×175
=549.5(平方米)
答:扩建后旱冰场的面积增加了549.5平方米。
【点睛】此题属于环形面积计算,根据环形面积公式:环形面积=外圆面积﹣内圆面积,或环形面积=3.14×(外圆半径的平方﹣内圆半径的平方);列式解答。
