(期中易错提升讲义)第二单元 长方体(一)(讲义)-2023-2024学年五年级下册数学下册北师大版(含答案)
文档属性
| 名称 | (期中易错提升讲义)第二单元 长方体(一)(讲义)-2023-2024学年五年级下册数学下册北师大版(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 336.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-04-16 15:02:30 | ||
图片预览




文档简介
第二单元 长方体(一)
考点1:长方体的特征
1.长方体有6个面.有三组相对的面完全相同.一般情况下六个面都是长方形,特殊情况时有两个面是正方形,其他四个面都是长方形,并且这四个面完全相同.
2.长方体有12条棱,相对的四条棱长度相等.按长度可分为三组,每一组有4条棱.
3.长方体有8个顶点.每个顶点连接三条棱.三条棱分别叫做长方体的长,宽,高.
4.长方体相邻的两条棱互相垂直.
考点2:正方体的特征
①8个顶点.
②12条棱,每条棱长度相等.
③相邻的两条棱互相垂直.
考点3:长方体的展开图
长方体展开图形如下情况:
考点4:长方体和正方体的表面积
长方体表面积:六个面积之和.
公式:S=2ab+2ah+2bh.(a表示底面的长,b表示底面的宽,h表示高)
正方体表面积:六个正方形面积之和.
公式:S=6a2.(a表示棱长)
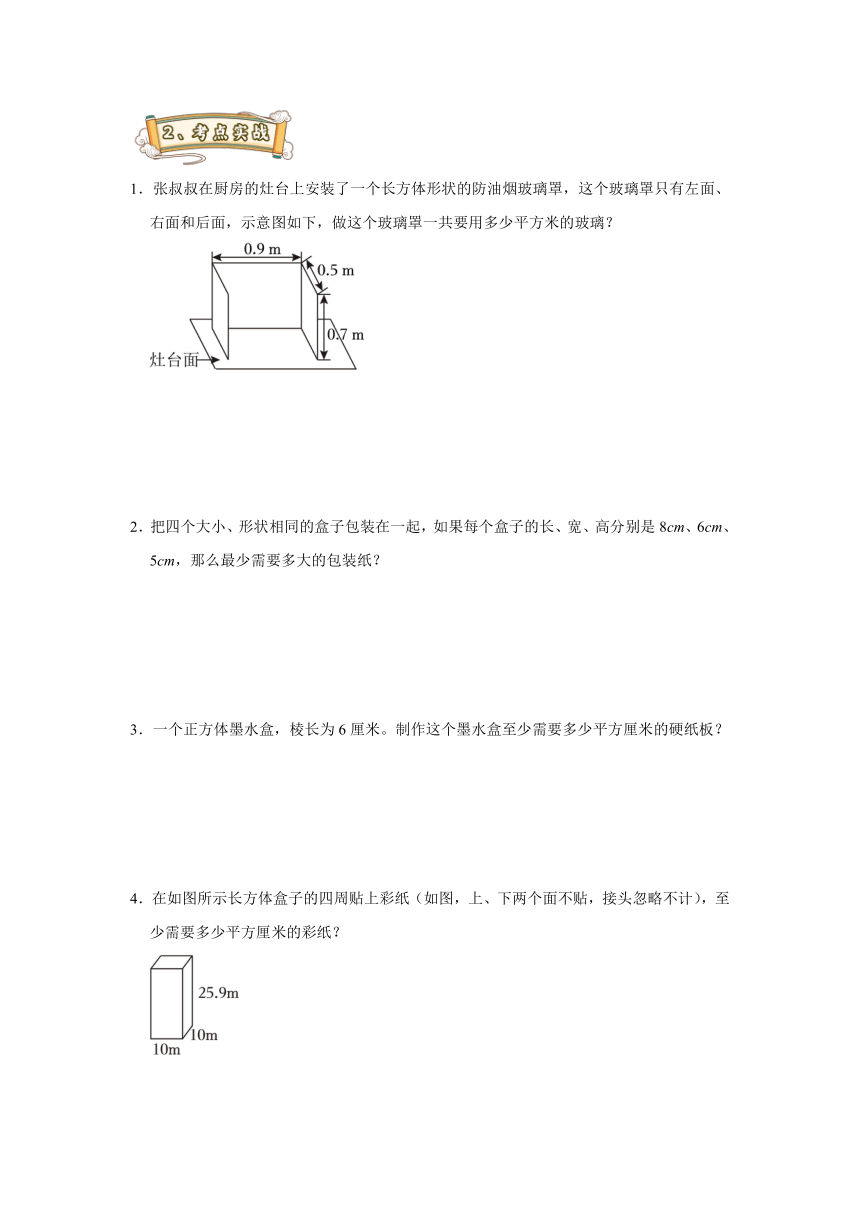
1.张叔叔在厨房的灶台上安装了一个长方体形状的防油烟玻璃罩,这个玻璃罩只有左面、右面和后面,示意图如下,做这个玻璃罩一共要用多少平方米的玻璃?
2.把四个大小、形状相同的盒子包装在一起,如果每个盒子的长、宽、高分别是8cm、6cm、5cm,那么最少需要多大的包装纸?
3.一个正方体墨水盒,棱长为6厘米。制作这个墨水盒至少需要多少平方厘米的硬纸板?
4.在如图所示长方体盒子的四周贴上彩纸(如图,上、下两个面不贴,接头忽略不计),至少需要多少平方厘米的彩纸?
5.一个长方体,长是35厘米、宽是30厘米、高是20厘米。这个长方体的表面积是多少平方厘米?
6.妈妈要给客厅的立式空调缝一个布罩(四周和顶部都要罩住),空调的样式如图所示。做这个布罩至少需要多少平方米布?
7.商店做了一个长为2m,宽为40cm,高为80cm的玻璃柜台。要在柜台各边都镶上铁皮,需要铁皮多少米?
8.梦歌同学想制作一个长方体的小盒子,方便大家存放闲置的小物品,他把小盒子裁开发现这个长方体的侧面(包括前、后、左、右面)展开和底面都是正方形,已知这个长方体的底面积是3平方分米。请大家帮忙算一算这个长方体的表面积?
9.挖一个长60m、宽30m、深2m的长方体水池,如果在水池的底面和侧面抹一层水泥,抹水泥的面积是多少平方米?
10.要将这个饼干盒的每个面都贴上商标纸,至少要多少平方分米的商标纸?
11.做一个铁皮通风管,长4米,通风口是周长0.8米的正方形,制作这样一个通风管至少需要多少平方分米铁皮?
12.一根底面是正方形的长方体木料,表面积为114cm2,锯去一个最大的正方体之后,余下的长方体的表面积为54cm2。那么锯下的正方体的表面积为多少平方厘米?
13.把一个棱长为6cm的正方体框架改做成一个长9cm、宽5cm的长方体框架,这个长方体框架的高是多少?
14.某超市,要做一个长2.3m,宽0.5m,高1.2m的玻璃柜台,现要在柜台各边都安上角铁,这个柜台需要多少米角铁?
15.已知一个长方体和一个正方体的棱长总和相等,且长方体的长是8厘米,宽是6厘米,高是10厘米,这个正方体的表面积是多少平方厘米?
16.学校要进行爱心捐赠活动,五(1)班准备做一个棱长4dm的正方体募捐箱,如果箱子的每个面都贴上红纸(开口处忽略不计),至少需要多少平方分米的红纸?
17.用一根铁丝正好可以做成一个棱长为6厘米的正方体框架,如果用这根铁丝做成一个长为8厘米、宽为3厘米的长方体框架,它的高是多少厘米?
18.学校会议室长20米,宽15米,高3米,如果给会议室地面铺上长1米,宽0.15米,厚0.03米的木地板,至少需要买多少块木地板?
19.如图,有一个长40厘米,宽和高都是2分米的长方体硬纸箱。用绳子将纸箱捆扎起来,打结处共用15厘米,一共要用绳子多少分米?
20.如图是一个无盖的长方体铁皮盒子,做这个盒子至少需要铁皮多少平方分米?
21.一根铁丝恰好焊接成一个长10dm,宽8dm,高6dm的长方体框架。若用这根铁丝焊接成一个最大的正方体框架,这个正方体框架的棱长是多少分米?
22.学校科技小组用一根60厘米长的铁丝做个长方体模型,这个长方体模型的长是6厘米,宽是5厘米,高是多少厘米?
23.赵叔叔用60cm长的铁丝正好做成了一个正方体框架,在这个正方体框架的表面糊上一层彩纸,至少需要多少平方厘米的彩纸?
24.学校运动会的领奖台除了底面不涂漆外,其它各面都涂漆,需要涂漆的面积是多少平方厘米?(单位:cm)(解答题,请写出主要解答过程)
25.小华的爸爸打算订做一个无盖的正方体鱼缸,棱长7分米,请你帮忙算一算,至少要用多少平方分米的玻璃呢?
26.超市要做一个长2.2m、宽40cm、高80cm的玻璃柜台。现在要在柜台各边都安上角铁,至少需要多少米的角铁?
27.张丽家要给一个长0.8米、宽0.5米、高1.6米的简易鞋柜换布罩(如图,没有底面)。至少需要用布多少平方米?
28.李阿姨用一根彩带为顾客捆扎一个食品盒,这个食品盒的长、宽、高分别为20厘米、10厘米、5厘米,如图那样捆扎并留下20厘米长作为手提环。这样一共需要多少分米长的彩带?
29.一种礼物的盒长10厘米,宽5厘米,高1厘米,小明要把这样的两盒礼物包装在一起,至少需要多少平方厘米的包装纸?(重叠部分忽略不计。)
30.王师傅用一根长38cm的铁丝焊接成一个正方体框架,还剩余了2cm。这个正方体框架的棱长是多少厘米?
31.有一个棱长是30厘米的正方体铁块,现在要把它熔铸成一个横截面积是90平方厘米的长方体,这个长方体的长是多少厘米?
32.一个长方体木块,沿着它的高截去3分米后变为一个正方体(如图),表面积减少了48平方分米,原来长方体的表面积是多少平方分米?
33.奇思用一根铁丝刚好围成一个长17cm,宽12cm,高19cm的长方体框架,若将这根铁丝改围成一个最大的正方体框架,这个正方体框架的棱长是多少厘米?
34.王大伯用钢筋焊接了一个长方体螃蟹养殖箱,一共用了116分米长的钢筋。已知养殖箱的长是15分米,宽是8分米,那么它的高是多少分米?
35.某健身馆计划新建一个游泳池,该游泳池长20米,宽12米,深1.5米。现在要在游泳池的四周和底面都贴上白瓷砖,需要贴白瓷砖的面积是多少平方米?
36.一个油箱的长是60cm,宽是50cm,高是40cm,做这个油箱至少要用多少平方分米的铁皮?
37.一根铁丝刚好围成一个棱长10cm的正方体框架,如果把它改围成一个长12cm,宽7cm的长方体框架,长方体框架的高是多少厘米?
38.一个无盖的长方体铁皮水箱,长5分米,宽4分米,高6分米.做一个这样的水箱至少要铁皮多少平方分米?(接口处不计)
39.胜利小学有一个长40米,宽15米,高4米的阶梯教室,给这个阶梯教室的四面墙壁和天花板粉刷油漆,粉刷的面积有多大?
40.王叔叔买木板做一个棱长是6分米的正方体木箱,每平方分米木板4元,做这个木箱共需要多少钱?
41.一个长方体的棱长总和是64分米,长是7分米,高是3分米,宽是长的几分之几?
42.一个无盖的长方体水桶,长25厘米,宽18厘米,高40厘米,做这个水桶至少用铁皮多少平方分米?(衔接处忽略不计)
43.乐乐为乡下的爷爷奶奶准备了中秋礼物,为了美观和神秘做了包装。如图包装这个礼盒需要多长的彩带?
44.一个长20厘米、宽15厘米、高10厘米的长方体礼盒,用如图的方式给它扎上彩带,接头处需要25厘米的彩带用于打结,包装这个礼盒需要用多少厘米的彩带?
45.如图是一个长方体铁盒的展开图,做这个铁盒需要多少平方厘米铁皮?
46.一只无盖的长方体水箱长45厘米,宽30厘米,高24厘米.制作这个水箱至少需要多少平方厘米铁皮?
47.一个正方体礼品盒,棱长1.2分米,如果包装这个礼品盒用的纸是其表面积的1.5倍,至少要用多少平方分米的包装纸?
48.一个通风管的横截面为正方形,边长为4分米,通风管长3米,做4节这样的通风管需要多少铁皮?
49.一个长方体的食品盒,长9cm,宽5cm,高4cm,如果围它贴一圈商标纸(上、下面不贴),这张商标纸的面积至少需要多少cm2?
参考答案
1.1.33平方米。
【分析】观察这个长方体玻璃罩,只有左面、右面和后面三个面的面积,左面和右面的面积利用(0.7×0.5)可求出,后面的面积可利用(0.9×0.7)求出,再把三个面的面积加起来,即可求出做这个玻璃罩一共要用多少平方米的玻璃。
【解答】解:0.7×0.5×2+0.9×0.7
=0.7+0.63
=1.33(平方米)
答:做这个玻璃罩一共要用1.33平方米的玻璃。
【点评】此题的解题关键是灵活运用长方体的表面积公式解决实际的问题。
2.592平方厘米。
【分析】根据题意,要使需要的包装纸最少,也就是把四个盒子的最大面重合起来,即四个盒子拼成一个长(6×2)厘米,宽(5×2)厘米,高8厘米的长方体。根据长方体的表面积公式:S=(ab+ah+bh)×2,把数据代入公式解答。
【解答】解:6×2=12(厘米)
5×2=10(厘米)
(12×10+12×8+10×8)×2
=(120+96+80)×2
=296×2
=592(平方厘米)
答:最少需要592平方厘米的包装纸。
【点评】此题主要考查长方体表面积公式的灵活运用,关键是熟记公式。
3.216平方厘米。
【分析】求制作这个正方体墨水盒至少需要硬纸板的面积,就是求正方体的表面积;根据正方体的表面积=棱长×棱长×6,代入数据计算即可。
【解答】解:6×6×6
=36×6
=216(平方厘米)
答:制作这个墨水盒至少需要216平方厘米的硬纸板。
【点评】本题考查的是正方体和长方体的面积计算公式,掌握正方体表面积的计算方法是解题的关键。
4.1036平方厘米。
【分析】在长方体盒子的四周贴上彩纸,求所用彩纸的面积就是求长方体盒子4个侧面积的和。
【解答】解:10×4×25.9
=40×25.9
=1036(平方厘米)
答:至少需要1036平方厘米的彩纸。
【点评】本题考查了长方体表面积的计算,解答本题的关键是确定求的是哪几个面的面积和。
5.4700平方厘米。
【分析】根据长方体的表面积公式:S=(ab+ah+bh)×2,把数据代入公式解答。
【解答】解:(35×30+35×20+30×20)×2
=(1050+700+600)×2
=2350×2
=4700(平方厘米)
答:这个长方体的表面积是4700平方厘米。
【点评】此题主要考查长方体表面积公式的灵活运用,关键是熟记公式。
6.2.12平方米。
【分析】根据生活经验可知,这个空调的布罩只有5个面,缺少下面,根据无底长方体的表面积公式:S=ab+2ah+2bh,把数据代入公式解答。
【解答】解:40厘米=0.4米
20厘米=0.2米
0.4×0.2+0.4×1.7×2+0.2×1.7×2
=0.08+1.36+0.68
=2.12(平方米)
答:做这个布罩至少需要2.12平方米布。
【点评】此题主要考查无底长方体表面积公式的灵活运用,关键是熟记公式。
7.12.8米。
【分析】根据长方体的特征,12条棱分为互相平行的3组,每组4条棱的长度相等,由题意可知,求这个柜台需要多少米角铁,也就是求这个长方体的棱长总和,根据长方体的棱长总和=(长+宽+高)×4,由此列式解答。
【解答】解:40厘米=0.4米
80厘米=0.8米
(2+0.4+0.8)×4
=3.2×4
=12.8(米)
答:需要12.8米。
【点评】此题属于长方体的棱长总和的实际应用,根据长方体的棱长总和的计算方法解决问题,注意单位的统一。
8.54平方分米。
【分析】由题意可知:这个长方体的侧面展开是一个正方形,说明底面周长和高相等,设底面边长为a分米,则高是(4a)分米,因为正方形的面积=边长×边长据此可以求出侧面积,再加上两个底面的面积即可解答问题。
【解答】解:设底面边长为a分米,则高是(4a)分米。
4a×4a+3×2
=16a2+6
=16×3+6
=48+6
=54(平方分米)
答:这个长方体的表面积是54平方分米。
【点评】此题主要考查正方形的周长公式、正方形的面积公式、长方体的表面积公式的灵活运用,关键是熟记公式。
9.2160平方米。
【分析】根据无盖长方体的表面积公式:S=ab+2ah+2bh,把数据代入公式解答。
【解答】解:60×30+60×2×2+30×2×2
=1800+240+120
=2160(平方米)
答:抹水泥的面积是2160平方米。
【点评】此题主要考查无盖长方体的表面积公式的灵活运用,关键是熟记公式。
10.78平方分米。
【分析】根据长方体的表面积公式:S=(ab+ah+bh)×2,把数据代入公式解答。
【解答】解(3×3+3×5+3×5)×2
=(9+15+15)×2
=39×2
=78(平方分米)
答:至少需要78平方分米的商标纸。
【点评】此题主要考查长方体表面积公式的灵活运用,关键是熟记公式。
11.320平方分米。
【分析】根据题干分析可得,此题就是利用底面周长乘通风管的长度,即求出通风管的侧面积。再换算单位即可,得数即为制作这样一个通风管至少需要多少平方分米铁皮。
【解答】解:4×0.8=3.2(平方米)
3.2平方米=320平方分米
答:制作这样一个通风管至少需要320平方分米铁皮。
【点评】本题考查长方体表面积的计算及应用。理解题意,找出数量关系,列式计算即可。
12.90平方厘米。
【分析】根据题意可知:锯下一个最大的正方体,这个正方体的棱长等于原来长方体的底面边长。表面积减少的是锯下的正方体的4个面的面积,由此可以求出锯下的正方体的一个面的面积,再乘6即可求出锯下的正方体的表面积。
【解答】解:原来长方体的底面积:
(114﹣54)÷4
=60÷4
=15(平方厘米)
15×6=90(平方厘米)
答:锯下的正方体的表面积是90平方厘米。
【点评】此题解答关键是求出原来长方体木料的底面的面积,即锯下的正方体的一个面的面积,再乘6即可解答。
13.4cm。
【分析】根据题意可知做成的正方体框架和长方体框架的棱长总和相等;据正方体的棱长总和=棱长×12,可计算出框架的总长,即长方体的棱长总和;再根据长方体的棱长总和=4×(长+宽+高),那么高=棱长总和÷4﹣长﹣宽。据此解答即可。
【解答】解:6×12÷4﹣9﹣5
=72÷4﹣9﹣5
=18﹣9﹣5
=4(cm)
答:这个长方体框架的高是4cm。
【点评】此题主要考查正方体、长方体棱长总和公式的灵活运用,关键是熟记公式。
14.16米。
【分析】根据长方体的棱长总和=(长+宽+高)×4,把数据代入公式解答即可。
【解答】解:(2.3+0.5+1.2)×4
=4×4
=16(米)
答:这个柜台需要16米角铁。
【点评】此题主要考查长方体的棱长总和公式的灵活运用,关键是熟记公式。
15.384平方厘米。
【分析】先求出长方体的棱长和,除以12得出正方体的棱长,再利用S=6a2求出正方体的表面积。
【解答】解:(6+8+10)×4
=24×4
=96(厘米)
96÷12=8(厘米)
8×8×6
=64×6
=384(平方厘米)
答:这个正方体的表面积是384平方厘米。
【点评】本题考查了正方体表面积的计算,需熟记公式准确计算。
16.96平方分米。
【分析】正方体的棱长是4dm,根据正方体的表面积公式:S=a2×6,代入数据解答即可。
【解答】解:4×4×6
=16×6
=96(平方分米)
答:至少需要96平方分米红纸。
【点评】此题主要考查了学生对正方体表面积公式的掌握应用情况。
17.7厘米。
【分析】用6×12=72(厘米),求出正方体的棱长和,因为正方体的棱长总和等于长方体的棱长总和,再根据长方体的棱长总和=(长+宽+高)×4,用棱长总和除以4减去长和宽即可求出高。
【解答】解:6×12÷4﹣8﹣3
=72÷4﹣8﹣3
=18﹣11
=7(厘米)
答:它的高是7厘米。
【点评】此题主要考查正方体,长方体的棱长总和公式的灵活运用。
18.2000块。
【分析】根据长方形的面积公式S=ab,先求出学校会议室地面的面积,再求出每块木地板的面积,最后用学校会议室地面的面积除以每块木地板的面积就是至少需要木地板的块数。
【解答】解:20×15÷(1×0.15)
=300÷0.15
=2000(块)
答:至少需要买2000块木地板。
【点评】此题主要考查了长方形的面积公式S=ab的灵活运用。
19.29.5分米。
【分析】绳子的总长包括2条长,4条宽,6条高及打结处的总长度,据此把长度相加即可。
【解答】解:40厘米=4分米
15厘米=1.5分米
4×2+2×6+2×4+1.5
=8+12+8+1.5
=29.5(分米)
答:一共要用绳子29.5分米。
【点评】此题主要考查长方体的特征及棱长总和的计算方法。
20.206。
【分析】根据长方体的表面积公式:S=(ab+ah+bh)×2,由于这个盒子无盖,所以只求它的5个面的总面积即可。
【解答】解:16×5+16×3×2+5×3×2
=80+96+30
=176+30
=206(平方分米)
答:做这个盒子至少需要铁皮206平方分米。
【点评】此题主要考查长方体表面积公式的灵活运用,关键是熟记公式。
21.8分米。
【分析】根据长方体的特征,12条棱分为互相平行的(相对的)3组,每组4条棱的长度相等,长方体的棱长总和=(长+宽+高)×4求出棱长总和,也就是正方体的棱长总和,正方体12条棱全部相等,利用棱长总和除以12即可。
【解答】解:(10+8+6)×4
=24×4
=96(分米)
96÷12=8(分米)
答:正方体的棱长是8分米。
【点评】本题考查了长方体和正方体的棱长总和的计算方法。
22.4厘米。
【分析】根据长方体的棱长总和=(长+宽+高)×4,用棱长总和除以4再减去长和宽的和即可。
【解答】解:60÷4﹣(6+5)
=15﹣11
=4(厘米)
答:高是4厘米。
【点评】本题主要考查长方体的棱长总和公式的灵活运用。
23.150平方厘米。
【分析】根据正方体的棱长总和=棱长×12,那么棱长=棱长总和÷12,据此求出棱长,再根据正方体的表面积公式:S=6a2,把数据代入公式解答。
【解答】解:60÷12=5(厘米)
5×5×6
=25×6
=150(平方厘米)
答:至少需要150平方厘米彩纸。
【点评】此题主要考查正方体的棱长总和公式、表面积公式的灵活运用,关键是熟记公式。
24.见试题解答内容
【分析】我们把这3个长方体的表面积分别计算再加在一起,两边的长方体有4个面,中间的5个面,这3个立体图形的前后是一样的.在计算的时候,左右的长方体计算:前、后、上,中间的长方体计算5个面即可.
【解答】解:(1)40×100×2+40×50+100×50×3+(40+30)×100×2+40×50+(40+30﹣40)×50+100×30×2+50×30
=8000+2000+15000+14000+2000+1500+6000+1500
=50000(平方厘米)
答:需要涂漆的面积是50000平方厘米.
【点评】本题借助实物考查了长方体的表面积公式及长方体的体积公式的运用,这里需要学生认真思考,发挥空间想象能力,认真解答.
25.245平方分米。
【分析】求需要用多少平方分米的玻璃,实际上是求这个正方体的5个面的面积和,根据求正方体表面积公式解答。
【解答】解:7×7×5
=49×5
=245(平方分米)
答:至少要用245平方分米的玻璃。
【点评】此题主要考查正方体表面积公式的灵活运用,关键是熟记公式。
26.13.6米。
【分析】根据长方体的棱长总和=(长+宽+高)×4,把数据代入公式解答即可。
【解答】解:40cm=0.4m
80cm=0.8m
(2.2+0.4+0.8)×4
=3.4×4
=13.6(m)
答:至少需要13.6米的角铁。
【点评】此题主要考查长方体的棱长总和公式的灵活运用,关键是熟记公式。
27.4.56平方米。
【分析】因简易鞋柜布罩(没有底面),求需要多少布,就是求这个长方体5个面的面积,根据长方体表面积的计算方法,解答即可。
【解答】解:0.8×0.5+0.8×1.6×2+0.5×1.6×2
=0.4+2.56+1.6
=4.56(平方米)
答:至少需要用布4.56平方米。
【点评】本题主要考查了学生对长方体表面积计算方法的掌握,注意本题求的是5个面的面积。
28.16分米。
【分析】由图可知,这样捆扎,长应该有4条,宽4条,高4条,再加手提环部分,计算完以后还要转换单位为分米。
【解答】解:20×4+10×4+5×4+20
=80+40+20+20
=160(厘米)
160厘米=16分米
答:这样一共需要16分米长的彩带。
【点评】此题属于长方体的棱长总和的实际应用,首先分清是如何捆扎的,然后根据棱长总和的计算方法解答。
29.160。
【分析】把这两个长方体盒子的10×5面相粘合,得到的大长方体的表面积最小,比原来两个盒子的表面积减少了2个最大的面,最节约包装纸。
【解答】解:(10×5+10×1+5×1)×2×2﹣10×5×2
=(50+10+5)×4﹣100
=65×4﹣100
=260﹣100
=160(平方厘米)
答:至少需要160平方厘米的包装纸。
【点评】抓住两个长方体拼组一个大长方体的方法:最大面相粘合,得到的大长方体的表面积最小;最小面相粘合,得到的大长方体的表面积最大。
30.3厘米。
【分析】正方体有12条棱,每条棱长度相等,棱长总和为12条棱的长度和,利用棱长总和除以12即可。
【解答】解:(38﹣2)÷12
=36÷12
=3(厘米)
答:这个正方体框架的棱长是3厘米。
【点评】此题考查计算正方体的棱长总和的方法,已知棱长总和求棱长除以12即可。
31.300厘米。
【分析】先利用正方体的体积V=a3,求出这块铁块的体积,因为这块铁块的体积是不变的,于是可以利用长方体的体积V=Sh求出溶铸成的长方体铁块的长度。
【解答】解:30×30×30÷90
=27000÷90
=300(厘米)
答:这个长方体的长是300厘米。
【点评】此题主要考查正方体和长方体的体积的计算方法在实际中的应用,关键是明白:这块铁块的体积是不变的。
32.144平方分米。
【分析】根据题意,高截去3分米,表面积减少了48平方分米,表面积减少的只是4个侧面的面积,又知剩下部分成为一个正方体,说明原来长方体的长和宽相等,由此可知,减少的4个侧面是完全相同的长方形,用减少的面积除以4求出一个面的面积,再用一个面的面积除以3分米,即可求出原来长方体的长和宽,用正方体的表面积加上减少的48平方分米就是原长方体的表面积。
【解答】解:原来长方体的长和宽是:
48÷4÷3
=12÷3
=4(分米)
4×4×6+48
=96+48
=144(平方分米)
答:原来长方体的表面积是144平方分米。
【点评】解答此题的关键是首先分析出表面积减少的只是4个侧面的面积,进而求出长方体的长、宽是多少。
33.16厘米。
【分析】根据长方体的特征,12条棱分为互相平行的(相对的)3组,每组4条棱的长度相等.长方体的棱长总和=(长+宽+高)×4,据此求出长方体的棱长总和,正方体的12条棱全部相等,再除以12即可求出正方体的棱长。
【解答】解:(17+12+19)×4÷12
=48×4÷12
=16(厘米)
答:这个正方体框架的棱长是16厘米。
【点评】此题主要考查长方体和正方体的特征及棱长总和的计算方法。
34.6分米。
【分析】根据长方体的特征,12条棱分为互相平行的(相对的)3组,每组4条棱的长度相等.长方体的棱长总和=(长+宽+高)×4,已知棱长总和是116分米,用棱长总和÷4求得长、宽、高的和,用长、宽、高的和减去长和宽就是它的高,由此列式解答。
【解答】解:116÷4﹣15﹣8
=29﹣15﹣8
=6(分米)
答:它的高是6分米。
【点评】此题主要考查长方体的特征及棱长总和的计算方法.根据棱长总和的计算方法解决问题。
35.336平方米。
【分析】求需要贴瓷砖的面积,就是求这个游泳池5个面积的面积和,即求这个游泳池的底面、前后面、左右面的面积之和;根据长×宽+(长×高+宽×高)×2,代入数据,即可解答。
【解答】解:20×12+(20×1.5+12×1.5)×2
=240+(30+18)×2
=240+48×2
=240+96
=336(平方米)
答:需要贴瓷砖的面积是336平方米。
【点评】熟练掌握长方体表面积公式是解答本题的关键。
36.148。
【分析】根据长方体的表面积公式:S=(ab+ah+bh)×2,把数据代入公式解答。
【解答】解:(60×50+60×40+50×40)×2
=(3000+2400+2000)×2
=7400×2
=14800(平方厘米)
14800平方厘米=148平方分米
答:做这个油箱至少要用148平方分米的铁皮。
【点评】此题主要考查长方体表面积公式的灵活运用,关键是熟记公式。
37.见试题解答内容
【分析】根据正方体的棱长总和=棱长×12,求出这根铁丝的长度,再根据长方体的棱长总和=(长+宽+高)×4,用棱长总和除以4再减去长和宽就是高.据此列式解答.
【解答】解;10×12=120(厘米)
120÷4﹣12﹣7
=30﹣12﹣7
=11(厘米)
答:长方体的高是11厘米.
【点评】此题考查的目的是理解掌握长方体、正方体棱长总和公式的灵活运用,关键是熟记公式.
38.见试题解答内容
【分析】首先搞清这道题是求长方体的表面积,其次这个长方体的表面由五个面组成,缺少上面,计算这五个面的面积和即可.
【解答】解:5×4+4×6×2+5×6×2
=20+48+60
=128(平方分米);
答:做一个这样的水箱至少要铁皮128平方分米.
【点评】这是一道长方体表面积的实际应用,在计算时要分清需要计算几个长方形面的面积,缺少的是哪一个面的面积,从而列式解答即可.
39.1040平方米。
【分析】首先搞清这道题是求长方体的表面积,其次这个房间(长方体)的表面由五个长方形组成,缺少下面,最后计算这五个面的面积和即可解决问题。
【解答】解:40×15+40×4×2+15×4×2
=600+320+120
=1040(平方米)
答:粉刷的面积有1040平方米。
【点评】这是一道长方体表面积的实际应用,在计算时要分清需要计算几个长方形面的面积,缺少的是哪一个面的面积,从而列式解答即可。
40.864元。
【分析】根据“正方体表面积=棱长×棱长×6”,把数据代入公式计算出这个正方体木箱的表面积,再乘木板的单价,据此解答即可。
【解答】解:6×6×6×4
=36×6×4
=216×4
=864(元)
答:做这个木箱共需要864元钱。
【点评】熟记正方体表面积计算公式,是解答此题的关键。
41.。
【分析】已知长方体棱长和是64分米,棱包括4组长宽高,那么一组长+宽+高的和是(64÷4)分米,再减去长和高即可求出宽,然后用宽除以长即可。
【解答】解:64÷4=16(分米)
16﹣7﹣3=6(分米)
6÷7
答:宽是长的。
【点评】此题考查了长方体棱长和的求法,要熟练掌握。结合题意分析解答即可。
42.38.9平方分米。
【分析】因是无盖的长方体铁水桶,所以一个水桶需要的木材的面积是5个面的面积,根据长方体表面积=长×宽×2+长×高×2+宽×高×2解答。
【解答】解:25×18+25×40×2+18×40×2
=450+2000+1440
=3890(平方厘米)
3890平方厘米=38.9平方分米
答:做这个水桶至少用铁皮38.9平方分米。
【点评】本题主要考查了学生对长方体表面积计算方法的题目。要注意单位的换算。
43.325厘米。
【分析】彩带的总长包括2条长、2条宽、4条高及蝴蝶结的长度,据此解答。
【解答】解:50×2+40×2+30×4+25
=100+80+120+25
=325(厘米)
答:包装这个礼盒需要325厘米的彩带。
【点评】此题主要考查长方体的特征及棱长总和的计算方法。
44.135厘米。
【分析】根据长方体的特征:12条棱分为互相平行的3组,每组4条棱的长度相等,由图形可知:需要彩带的长度等于2条长+4条高+2条宽+打结用的25厘米即可。
【解答】解:20×2+15×2+10×4+25
=40+30+40+25
=135(厘米)
答:至少需要135厘米的彩带。
【点评】此题考查的目的是理解掌握长方体的特征,以及长方体棱长总和的计算方法,结合题意分析解答即可。
45.700。
【分析】根据题意,铁皮的面积=长方形面积﹣四个小正方形面积,据此解答。
【解答】解:40×20﹣5×5×4
=800﹣100
=700(平方厘米)
答:做这个铁盒需要700平方厘米铁皮。
【点评】本题考查了长方体的展开图问题,解决本题的关键是将铁皮的面积转化成长方形和正方形的面积。
46.见试题解答内容
【分析】做这个水箱至少需要多少平方分米铁皮,首先明确它无盖,是求它的5个面的总面积,根据长方体的表面积的计算方法解答.
【解答】解:45×30+(30×24+24×45)×2
=1350+(720+1080)×2
=1350+1800×2
=1350+3600
=4950(平方厘米)
答:制作这个水箱至少需要4950平方厘米铁皮.
【点评】这是一道长方体表面积的实际应用,在计算表面积时要分清需要计算几个面的面积,缺少的是哪一个面的面积,从而列式解答即可.
47.12.96平方分米。
【分析】根据正方体的表面积公式:S=6a2,把数据代入公式求出这个礼品盒表面积,再乘上1.5即可解答。
【解答】解:1.2×1.2×6×1.5
=1.44×6×1.5
=8.64×1.5
=12.96(平方分米)
答:至少要用12.96平方分米的包装纸。
【点评】此题主要考查正方体表面积公式的灵活运用,关键是熟记公式。
48.1920平方分米。
【分析】做4节这样的通风管需要铁皮的面积=平均每节铁皮的面积×节数;其中,平均每节铁皮的面积=横截面的周长×长;横截面的周长=横截面的边长×4。
【解答】解:3米=30分米
4×4×30×4
=16×30×4
=480×4
=1920(平方分米)
答:做4节这样的通风管需要1920平方分米铁皮。
【点评】本题考查了长方体的表面积公式的应用。
49.112cm2。
【分析】上下面不贴,就是在左右面和前后面四个面贴上商标纸,求出这四个面的面积和即可。
【解答】解:(9×4+5×4)×2
=(36+20)×2
=56×2
=112(cm2)
答:这张商标纸的面积至少需要112cm2。
【点评】此题考查长方体表面积的实际应用,在计算时要分清需要计算几个长方形面的面积,缺少的是哪些面的面积,从而列式解答即可。
考点1:长方体的特征
1.长方体有6个面.有三组相对的面完全相同.一般情况下六个面都是长方形,特殊情况时有两个面是正方形,其他四个面都是长方形,并且这四个面完全相同.
2.长方体有12条棱,相对的四条棱长度相等.按长度可分为三组,每一组有4条棱.
3.长方体有8个顶点.每个顶点连接三条棱.三条棱分别叫做长方体的长,宽,高.
4.长方体相邻的两条棱互相垂直.
考点2:正方体的特征
①8个顶点.
②12条棱,每条棱长度相等.
③相邻的两条棱互相垂直.
考点3:长方体的展开图
长方体展开图形如下情况:
考点4:长方体和正方体的表面积
长方体表面积:六个面积之和.
公式:S=2ab+2ah+2bh.(a表示底面的长,b表示底面的宽,h表示高)
正方体表面积:六个正方形面积之和.
公式:S=6a2.(a表示棱长)
1.张叔叔在厨房的灶台上安装了一个长方体形状的防油烟玻璃罩,这个玻璃罩只有左面、右面和后面,示意图如下,做这个玻璃罩一共要用多少平方米的玻璃?
2.把四个大小、形状相同的盒子包装在一起,如果每个盒子的长、宽、高分别是8cm、6cm、5cm,那么最少需要多大的包装纸?
3.一个正方体墨水盒,棱长为6厘米。制作这个墨水盒至少需要多少平方厘米的硬纸板?
4.在如图所示长方体盒子的四周贴上彩纸(如图,上、下两个面不贴,接头忽略不计),至少需要多少平方厘米的彩纸?
5.一个长方体,长是35厘米、宽是30厘米、高是20厘米。这个长方体的表面积是多少平方厘米?
6.妈妈要给客厅的立式空调缝一个布罩(四周和顶部都要罩住),空调的样式如图所示。做这个布罩至少需要多少平方米布?
7.商店做了一个长为2m,宽为40cm,高为80cm的玻璃柜台。要在柜台各边都镶上铁皮,需要铁皮多少米?
8.梦歌同学想制作一个长方体的小盒子,方便大家存放闲置的小物品,他把小盒子裁开发现这个长方体的侧面(包括前、后、左、右面)展开和底面都是正方形,已知这个长方体的底面积是3平方分米。请大家帮忙算一算这个长方体的表面积?
9.挖一个长60m、宽30m、深2m的长方体水池,如果在水池的底面和侧面抹一层水泥,抹水泥的面积是多少平方米?
10.要将这个饼干盒的每个面都贴上商标纸,至少要多少平方分米的商标纸?
11.做一个铁皮通风管,长4米,通风口是周长0.8米的正方形,制作这样一个通风管至少需要多少平方分米铁皮?
12.一根底面是正方形的长方体木料,表面积为114cm2,锯去一个最大的正方体之后,余下的长方体的表面积为54cm2。那么锯下的正方体的表面积为多少平方厘米?
13.把一个棱长为6cm的正方体框架改做成一个长9cm、宽5cm的长方体框架,这个长方体框架的高是多少?
14.某超市,要做一个长2.3m,宽0.5m,高1.2m的玻璃柜台,现要在柜台各边都安上角铁,这个柜台需要多少米角铁?
15.已知一个长方体和一个正方体的棱长总和相等,且长方体的长是8厘米,宽是6厘米,高是10厘米,这个正方体的表面积是多少平方厘米?
16.学校要进行爱心捐赠活动,五(1)班准备做一个棱长4dm的正方体募捐箱,如果箱子的每个面都贴上红纸(开口处忽略不计),至少需要多少平方分米的红纸?
17.用一根铁丝正好可以做成一个棱长为6厘米的正方体框架,如果用这根铁丝做成一个长为8厘米、宽为3厘米的长方体框架,它的高是多少厘米?
18.学校会议室长20米,宽15米,高3米,如果给会议室地面铺上长1米,宽0.15米,厚0.03米的木地板,至少需要买多少块木地板?
19.如图,有一个长40厘米,宽和高都是2分米的长方体硬纸箱。用绳子将纸箱捆扎起来,打结处共用15厘米,一共要用绳子多少分米?
20.如图是一个无盖的长方体铁皮盒子,做这个盒子至少需要铁皮多少平方分米?
21.一根铁丝恰好焊接成一个长10dm,宽8dm,高6dm的长方体框架。若用这根铁丝焊接成一个最大的正方体框架,这个正方体框架的棱长是多少分米?
22.学校科技小组用一根60厘米长的铁丝做个长方体模型,这个长方体模型的长是6厘米,宽是5厘米,高是多少厘米?
23.赵叔叔用60cm长的铁丝正好做成了一个正方体框架,在这个正方体框架的表面糊上一层彩纸,至少需要多少平方厘米的彩纸?
24.学校运动会的领奖台除了底面不涂漆外,其它各面都涂漆,需要涂漆的面积是多少平方厘米?(单位:cm)(解答题,请写出主要解答过程)
25.小华的爸爸打算订做一个无盖的正方体鱼缸,棱长7分米,请你帮忙算一算,至少要用多少平方分米的玻璃呢?
26.超市要做一个长2.2m、宽40cm、高80cm的玻璃柜台。现在要在柜台各边都安上角铁,至少需要多少米的角铁?
27.张丽家要给一个长0.8米、宽0.5米、高1.6米的简易鞋柜换布罩(如图,没有底面)。至少需要用布多少平方米?
28.李阿姨用一根彩带为顾客捆扎一个食品盒,这个食品盒的长、宽、高分别为20厘米、10厘米、5厘米,如图那样捆扎并留下20厘米长作为手提环。这样一共需要多少分米长的彩带?
29.一种礼物的盒长10厘米,宽5厘米,高1厘米,小明要把这样的两盒礼物包装在一起,至少需要多少平方厘米的包装纸?(重叠部分忽略不计。)
30.王师傅用一根长38cm的铁丝焊接成一个正方体框架,还剩余了2cm。这个正方体框架的棱长是多少厘米?
31.有一个棱长是30厘米的正方体铁块,现在要把它熔铸成一个横截面积是90平方厘米的长方体,这个长方体的长是多少厘米?
32.一个长方体木块,沿着它的高截去3分米后变为一个正方体(如图),表面积减少了48平方分米,原来长方体的表面积是多少平方分米?
33.奇思用一根铁丝刚好围成一个长17cm,宽12cm,高19cm的长方体框架,若将这根铁丝改围成一个最大的正方体框架,这个正方体框架的棱长是多少厘米?
34.王大伯用钢筋焊接了一个长方体螃蟹养殖箱,一共用了116分米长的钢筋。已知养殖箱的长是15分米,宽是8分米,那么它的高是多少分米?
35.某健身馆计划新建一个游泳池,该游泳池长20米,宽12米,深1.5米。现在要在游泳池的四周和底面都贴上白瓷砖,需要贴白瓷砖的面积是多少平方米?
36.一个油箱的长是60cm,宽是50cm,高是40cm,做这个油箱至少要用多少平方分米的铁皮?
37.一根铁丝刚好围成一个棱长10cm的正方体框架,如果把它改围成一个长12cm,宽7cm的长方体框架,长方体框架的高是多少厘米?
38.一个无盖的长方体铁皮水箱,长5分米,宽4分米,高6分米.做一个这样的水箱至少要铁皮多少平方分米?(接口处不计)
39.胜利小学有一个长40米,宽15米,高4米的阶梯教室,给这个阶梯教室的四面墙壁和天花板粉刷油漆,粉刷的面积有多大?
40.王叔叔买木板做一个棱长是6分米的正方体木箱,每平方分米木板4元,做这个木箱共需要多少钱?
41.一个长方体的棱长总和是64分米,长是7分米,高是3分米,宽是长的几分之几?
42.一个无盖的长方体水桶,长25厘米,宽18厘米,高40厘米,做这个水桶至少用铁皮多少平方分米?(衔接处忽略不计)
43.乐乐为乡下的爷爷奶奶准备了中秋礼物,为了美观和神秘做了包装。如图包装这个礼盒需要多长的彩带?
44.一个长20厘米、宽15厘米、高10厘米的长方体礼盒,用如图的方式给它扎上彩带,接头处需要25厘米的彩带用于打结,包装这个礼盒需要用多少厘米的彩带?
45.如图是一个长方体铁盒的展开图,做这个铁盒需要多少平方厘米铁皮?
46.一只无盖的长方体水箱长45厘米,宽30厘米,高24厘米.制作这个水箱至少需要多少平方厘米铁皮?
47.一个正方体礼品盒,棱长1.2分米,如果包装这个礼品盒用的纸是其表面积的1.5倍,至少要用多少平方分米的包装纸?
48.一个通风管的横截面为正方形,边长为4分米,通风管长3米,做4节这样的通风管需要多少铁皮?
49.一个长方体的食品盒,长9cm,宽5cm,高4cm,如果围它贴一圈商标纸(上、下面不贴),这张商标纸的面积至少需要多少cm2?
参考答案
1.1.33平方米。
【分析】观察这个长方体玻璃罩,只有左面、右面和后面三个面的面积,左面和右面的面积利用(0.7×0.5)可求出,后面的面积可利用(0.9×0.7)求出,再把三个面的面积加起来,即可求出做这个玻璃罩一共要用多少平方米的玻璃。
【解答】解:0.7×0.5×2+0.9×0.7
=0.7+0.63
=1.33(平方米)
答:做这个玻璃罩一共要用1.33平方米的玻璃。
【点评】此题的解题关键是灵活运用长方体的表面积公式解决实际的问题。
2.592平方厘米。
【分析】根据题意,要使需要的包装纸最少,也就是把四个盒子的最大面重合起来,即四个盒子拼成一个长(6×2)厘米,宽(5×2)厘米,高8厘米的长方体。根据长方体的表面积公式:S=(ab+ah+bh)×2,把数据代入公式解答。
【解答】解:6×2=12(厘米)
5×2=10(厘米)
(12×10+12×8+10×8)×2
=(120+96+80)×2
=296×2
=592(平方厘米)
答:最少需要592平方厘米的包装纸。
【点评】此题主要考查长方体表面积公式的灵活运用,关键是熟记公式。
3.216平方厘米。
【分析】求制作这个正方体墨水盒至少需要硬纸板的面积,就是求正方体的表面积;根据正方体的表面积=棱长×棱长×6,代入数据计算即可。
【解答】解:6×6×6
=36×6
=216(平方厘米)
答:制作这个墨水盒至少需要216平方厘米的硬纸板。
【点评】本题考查的是正方体和长方体的面积计算公式,掌握正方体表面积的计算方法是解题的关键。
4.1036平方厘米。
【分析】在长方体盒子的四周贴上彩纸,求所用彩纸的面积就是求长方体盒子4个侧面积的和。
【解答】解:10×4×25.9
=40×25.9
=1036(平方厘米)
答:至少需要1036平方厘米的彩纸。
【点评】本题考查了长方体表面积的计算,解答本题的关键是确定求的是哪几个面的面积和。
5.4700平方厘米。
【分析】根据长方体的表面积公式:S=(ab+ah+bh)×2,把数据代入公式解答。
【解答】解:(35×30+35×20+30×20)×2
=(1050+700+600)×2
=2350×2
=4700(平方厘米)
答:这个长方体的表面积是4700平方厘米。
【点评】此题主要考查长方体表面积公式的灵活运用,关键是熟记公式。
6.2.12平方米。
【分析】根据生活经验可知,这个空调的布罩只有5个面,缺少下面,根据无底长方体的表面积公式:S=ab+2ah+2bh,把数据代入公式解答。
【解答】解:40厘米=0.4米
20厘米=0.2米
0.4×0.2+0.4×1.7×2+0.2×1.7×2
=0.08+1.36+0.68
=2.12(平方米)
答:做这个布罩至少需要2.12平方米布。
【点评】此题主要考查无底长方体表面积公式的灵活运用,关键是熟记公式。
7.12.8米。
【分析】根据长方体的特征,12条棱分为互相平行的3组,每组4条棱的长度相等,由题意可知,求这个柜台需要多少米角铁,也就是求这个长方体的棱长总和,根据长方体的棱长总和=(长+宽+高)×4,由此列式解答。
【解答】解:40厘米=0.4米
80厘米=0.8米
(2+0.4+0.8)×4
=3.2×4
=12.8(米)
答:需要12.8米。
【点评】此题属于长方体的棱长总和的实际应用,根据长方体的棱长总和的计算方法解决问题,注意单位的统一。
8.54平方分米。
【分析】由题意可知:这个长方体的侧面展开是一个正方形,说明底面周长和高相等,设底面边长为a分米,则高是(4a)分米,因为正方形的面积=边长×边长据此可以求出侧面积,再加上两个底面的面积即可解答问题。
【解答】解:设底面边长为a分米,则高是(4a)分米。
4a×4a+3×2
=16a2+6
=16×3+6
=48+6
=54(平方分米)
答:这个长方体的表面积是54平方分米。
【点评】此题主要考查正方形的周长公式、正方形的面积公式、长方体的表面积公式的灵活运用,关键是熟记公式。
9.2160平方米。
【分析】根据无盖长方体的表面积公式:S=ab+2ah+2bh,把数据代入公式解答。
【解答】解:60×30+60×2×2+30×2×2
=1800+240+120
=2160(平方米)
答:抹水泥的面积是2160平方米。
【点评】此题主要考查无盖长方体的表面积公式的灵活运用,关键是熟记公式。
10.78平方分米。
【分析】根据长方体的表面积公式:S=(ab+ah+bh)×2,把数据代入公式解答。
【解答】解(3×3+3×5+3×5)×2
=(9+15+15)×2
=39×2
=78(平方分米)
答:至少需要78平方分米的商标纸。
【点评】此题主要考查长方体表面积公式的灵活运用,关键是熟记公式。
11.320平方分米。
【分析】根据题干分析可得,此题就是利用底面周长乘通风管的长度,即求出通风管的侧面积。再换算单位即可,得数即为制作这样一个通风管至少需要多少平方分米铁皮。
【解答】解:4×0.8=3.2(平方米)
3.2平方米=320平方分米
答:制作这样一个通风管至少需要320平方分米铁皮。
【点评】本题考查长方体表面积的计算及应用。理解题意,找出数量关系,列式计算即可。
12.90平方厘米。
【分析】根据题意可知:锯下一个最大的正方体,这个正方体的棱长等于原来长方体的底面边长。表面积减少的是锯下的正方体的4个面的面积,由此可以求出锯下的正方体的一个面的面积,再乘6即可求出锯下的正方体的表面积。
【解答】解:原来长方体的底面积:
(114﹣54)÷4
=60÷4
=15(平方厘米)
15×6=90(平方厘米)
答:锯下的正方体的表面积是90平方厘米。
【点评】此题解答关键是求出原来长方体木料的底面的面积,即锯下的正方体的一个面的面积,再乘6即可解答。
13.4cm。
【分析】根据题意可知做成的正方体框架和长方体框架的棱长总和相等;据正方体的棱长总和=棱长×12,可计算出框架的总长,即长方体的棱长总和;再根据长方体的棱长总和=4×(长+宽+高),那么高=棱长总和÷4﹣长﹣宽。据此解答即可。
【解答】解:6×12÷4﹣9﹣5
=72÷4﹣9﹣5
=18﹣9﹣5
=4(cm)
答:这个长方体框架的高是4cm。
【点评】此题主要考查正方体、长方体棱长总和公式的灵活运用,关键是熟记公式。
14.16米。
【分析】根据长方体的棱长总和=(长+宽+高)×4,把数据代入公式解答即可。
【解答】解:(2.3+0.5+1.2)×4
=4×4
=16(米)
答:这个柜台需要16米角铁。
【点评】此题主要考查长方体的棱长总和公式的灵活运用,关键是熟记公式。
15.384平方厘米。
【分析】先求出长方体的棱长和,除以12得出正方体的棱长,再利用S=6a2求出正方体的表面积。
【解答】解:(6+8+10)×4
=24×4
=96(厘米)
96÷12=8(厘米)
8×8×6
=64×6
=384(平方厘米)
答:这个正方体的表面积是384平方厘米。
【点评】本题考查了正方体表面积的计算,需熟记公式准确计算。
16.96平方分米。
【分析】正方体的棱长是4dm,根据正方体的表面积公式:S=a2×6,代入数据解答即可。
【解答】解:4×4×6
=16×6
=96(平方分米)
答:至少需要96平方分米红纸。
【点评】此题主要考查了学生对正方体表面积公式的掌握应用情况。
17.7厘米。
【分析】用6×12=72(厘米),求出正方体的棱长和,因为正方体的棱长总和等于长方体的棱长总和,再根据长方体的棱长总和=(长+宽+高)×4,用棱长总和除以4减去长和宽即可求出高。
【解答】解:6×12÷4﹣8﹣3
=72÷4﹣8﹣3
=18﹣11
=7(厘米)
答:它的高是7厘米。
【点评】此题主要考查正方体,长方体的棱长总和公式的灵活运用。
18.2000块。
【分析】根据长方形的面积公式S=ab,先求出学校会议室地面的面积,再求出每块木地板的面积,最后用学校会议室地面的面积除以每块木地板的面积就是至少需要木地板的块数。
【解答】解:20×15÷(1×0.15)
=300÷0.15
=2000(块)
答:至少需要买2000块木地板。
【点评】此题主要考查了长方形的面积公式S=ab的灵活运用。
19.29.5分米。
【分析】绳子的总长包括2条长,4条宽,6条高及打结处的总长度,据此把长度相加即可。
【解答】解:40厘米=4分米
15厘米=1.5分米
4×2+2×6+2×4+1.5
=8+12+8+1.5
=29.5(分米)
答:一共要用绳子29.5分米。
【点评】此题主要考查长方体的特征及棱长总和的计算方法。
20.206。
【分析】根据长方体的表面积公式:S=(ab+ah+bh)×2,由于这个盒子无盖,所以只求它的5个面的总面积即可。
【解答】解:16×5+16×3×2+5×3×2
=80+96+30
=176+30
=206(平方分米)
答:做这个盒子至少需要铁皮206平方分米。
【点评】此题主要考查长方体表面积公式的灵活运用,关键是熟记公式。
21.8分米。
【分析】根据长方体的特征,12条棱分为互相平行的(相对的)3组,每组4条棱的长度相等,长方体的棱长总和=(长+宽+高)×4求出棱长总和,也就是正方体的棱长总和,正方体12条棱全部相等,利用棱长总和除以12即可。
【解答】解:(10+8+6)×4
=24×4
=96(分米)
96÷12=8(分米)
答:正方体的棱长是8分米。
【点评】本题考查了长方体和正方体的棱长总和的计算方法。
22.4厘米。
【分析】根据长方体的棱长总和=(长+宽+高)×4,用棱长总和除以4再减去长和宽的和即可。
【解答】解:60÷4﹣(6+5)
=15﹣11
=4(厘米)
答:高是4厘米。
【点评】本题主要考查长方体的棱长总和公式的灵活运用。
23.150平方厘米。
【分析】根据正方体的棱长总和=棱长×12,那么棱长=棱长总和÷12,据此求出棱长,再根据正方体的表面积公式:S=6a2,把数据代入公式解答。
【解答】解:60÷12=5(厘米)
5×5×6
=25×6
=150(平方厘米)
答:至少需要150平方厘米彩纸。
【点评】此题主要考查正方体的棱长总和公式、表面积公式的灵活运用,关键是熟记公式。
24.见试题解答内容
【分析】我们把这3个长方体的表面积分别计算再加在一起,两边的长方体有4个面,中间的5个面,这3个立体图形的前后是一样的.在计算的时候,左右的长方体计算:前、后、上,中间的长方体计算5个面即可.
【解答】解:(1)40×100×2+40×50+100×50×3+(40+30)×100×2+40×50+(40+30﹣40)×50+100×30×2+50×30
=8000+2000+15000+14000+2000+1500+6000+1500
=50000(平方厘米)
答:需要涂漆的面积是50000平方厘米.
【点评】本题借助实物考查了长方体的表面积公式及长方体的体积公式的运用,这里需要学生认真思考,发挥空间想象能力,认真解答.
25.245平方分米。
【分析】求需要用多少平方分米的玻璃,实际上是求这个正方体的5个面的面积和,根据求正方体表面积公式解答。
【解答】解:7×7×5
=49×5
=245(平方分米)
答:至少要用245平方分米的玻璃。
【点评】此题主要考查正方体表面积公式的灵活运用,关键是熟记公式。
26.13.6米。
【分析】根据长方体的棱长总和=(长+宽+高)×4,把数据代入公式解答即可。
【解答】解:40cm=0.4m
80cm=0.8m
(2.2+0.4+0.8)×4
=3.4×4
=13.6(m)
答:至少需要13.6米的角铁。
【点评】此题主要考查长方体的棱长总和公式的灵活运用,关键是熟记公式。
27.4.56平方米。
【分析】因简易鞋柜布罩(没有底面),求需要多少布,就是求这个长方体5个面的面积,根据长方体表面积的计算方法,解答即可。
【解答】解:0.8×0.5+0.8×1.6×2+0.5×1.6×2
=0.4+2.56+1.6
=4.56(平方米)
答:至少需要用布4.56平方米。
【点评】本题主要考查了学生对长方体表面积计算方法的掌握,注意本题求的是5个面的面积。
28.16分米。
【分析】由图可知,这样捆扎,长应该有4条,宽4条,高4条,再加手提环部分,计算完以后还要转换单位为分米。
【解答】解:20×4+10×4+5×4+20
=80+40+20+20
=160(厘米)
160厘米=16分米
答:这样一共需要16分米长的彩带。
【点评】此题属于长方体的棱长总和的实际应用,首先分清是如何捆扎的,然后根据棱长总和的计算方法解答。
29.160。
【分析】把这两个长方体盒子的10×5面相粘合,得到的大长方体的表面积最小,比原来两个盒子的表面积减少了2个最大的面,最节约包装纸。
【解答】解:(10×5+10×1+5×1)×2×2﹣10×5×2
=(50+10+5)×4﹣100
=65×4﹣100
=260﹣100
=160(平方厘米)
答:至少需要160平方厘米的包装纸。
【点评】抓住两个长方体拼组一个大长方体的方法:最大面相粘合,得到的大长方体的表面积最小;最小面相粘合,得到的大长方体的表面积最大。
30.3厘米。
【分析】正方体有12条棱,每条棱长度相等,棱长总和为12条棱的长度和,利用棱长总和除以12即可。
【解答】解:(38﹣2)÷12
=36÷12
=3(厘米)
答:这个正方体框架的棱长是3厘米。
【点评】此题考查计算正方体的棱长总和的方法,已知棱长总和求棱长除以12即可。
31.300厘米。
【分析】先利用正方体的体积V=a3,求出这块铁块的体积,因为这块铁块的体积是不变的,于是可以利用长方体的体积V=Sh求出溶铸成的长方体铁块的长度。
【解答】解:30×30×30÷90
=27000÷90
=300(厘米)
答:这个长方体的长是300厘米。
【点评】此题主要考查正方体和长方体的体积的计算方法在实际中的应用,关键是明白:这块铁块的体积是不变的。
32.144平方分米。
【分析】根据题意,高截去3分米,表面积减少了48平方分米,表面积减少的只是4个侧面的面积,又知剩下部分成为一个正方体,说明原来长方体的长和宽相等,由此可知,减少的4个侧面是完全相同的长方形,用减少的面积除以4求出一个面的面积,再用一个面的面积除以3分米,即可求出原来长方体的长和宽,用正方体的表面积加上减少的48平方分米就是原长方体的表面积。
【解答】解:原来长方体的长和宽是:
48÷4÷3
=12÷3
=4(分米)
4×4×6+48
=96+48
=144(平方分米)
答:原来长方体的表面积是144平方分米。
【点评】解答此题的关键是首先分析出表面积减少的只是4个侧面的面积,进而求出长方体的长、宽是多少。
33.16厘米。
【分析】根据长方体的特征,12条棱分为互相平行的(相对的)3组,每组4条棱的长度相等.长方体的棱长总和=(长+宽+高)×4,据此求出长方体的棱长总和,正方体的12条棱全部相等,再除以12即可求出正方体的棱长。
【解答】解:(17+12+19)×4÷12
=48×4÷12
=16(厘米)
答:这个正方体框架的棱长是16厘米。
【点评】此题主要考查长方体和正方体的特征及棱长总和的计算方法。
34.6分米。
【分析】根据长方体的特征,12条棱分为互相平行的(相对的)3组,每组4条棱的长度相等.长方体的棱长总和=(长+宽+高)×4,已知棱长总和是116分米,用棱长总和÷4求得长、宽、高的和,用长、宽、高的和减去长和宽就是它的高,由此列式解答。
【解答】解:116÷4﹣15﹣8
=29﹣15﹣8
=6(分米)
答:它的高是6分米。
【点评】此题主要考查长方体的特征及棱长总和的计算方法.根据棱长总和的计算方法解决问题。
35.336平方米。
【分析】求需要贴瓷砖的面积,就是求这个游泳池5个面积的面积和,即求这个游泳池的底面、前后面、左右面的面积之和;根据长×宽+(长×高+宽×高)×2,代入数据,即可解答。
【解答】解:20×12+(20×1.5+12×1.5)×2
=240+(30+18)×2
=240+48×2
=240+96
=336(平方米)
答:需要贴瓷砖的面积是336平方米。
【点评】熟练掌握长方体表面积公式是解答本题的关键。
36.148。
【分析】根据长方体的表面积公式:S=(ab+ah+bh)×2,把数据代入公式解答。
【解答】解:(60×50+60×40+50×40)×2
=(3000+2400+2000)×2
=7400×2
=14800(平方厘米)
14800平方厘米=148平方分米
答:做这个油箱至少要用148平方分米的铁皮。
【点评】此题主要考查长方体表面积公式的灵活运用,关键是熟记公式。
37.见试题解答内容
【分析】根据正方体的棱长总和=棱长×12,求出这根铁丝的长度,再根据长方体的棱长总和=(长+宽+高)×4,用棱长总和除以4再减去长和宽就是高.据此列式解答.
【解答】解;10×12=120(厘米)
120÷4﹣12﹣7
=30﹣12﹣7
=11(厘米)
答:长方体的高是11厘米.
【点评】此题考查的目的是理解掌握长方体、正方体棱长总和公式的灵活运用,关键是熟记公式.
38.见试题解答内容
【分析】首先搞清这道题是求长方体的表面积,其次这个长方体的表面由五个面组成,缺少上面,计算这五个面的面积和即可.
【解答】解:5×4+4×6×2+5×6×2
=20+48+60
=128(平方分米);
答:做一个这样的水箱至少要铁皮128平方分米.
【点评】这是一道长方体表面积的实际应用,在计算时要分清需要计算几个长方形面的面积,缺少的是哪一个面的面积,从而列式解答即可.
39.1040平方米。
【分析】首先搞清这道题是求长方体的表面积,其次这个房间(长方体)的表面由五个长方形组成,缺少下面,最后计算这五个面的面积和即可解决问题。
【解答】解:40×15+40×4×2+15×4×2
=600+320+120
=1040(平方米)
答:粉刷的面积有1040平方米。
【点评】这是一道长方体表面积的实际应用,在计算时要分清需要计算几个长方形面的面积,缺少的是哪一个面的面积,从而列式解答即可。
40.864元。
【分析】根据“正方体表面积=棱长×棱长×6”,把数据代入公式计算出这个正方体木箱的表面积,再乘木板的单价,据此解答即可。
【解答】解:6×6×6×4
=36×6×4
=216×4
=864(元)
答:做这个木箱共需要864元钱。
【点评】熟记正方体表面积计算公式,是解答此题的关键。
41.。
【分析】已知长方体棱长和是64分米,棱包括4组长宽高,那么一组长+宽+高的和是(64÷4)分米,再减去长和高即可求出宽,然后用宽除以长即可。
【解答】解:64÷4=16(分米)
16﹣7﹣3=6(分米)
6÷7
答:宽是长的。
【点评】此题考查了长方体棱长和的求法,要熟练掌握。结合题意分析解答即可。
42.38.9平方分米。
【分析】因是无盖的长方体铁水桶,所以一个水桶需要的木材的面积是5个面的面积,根据长方体表面积=长×宽×2+长×高×2+宽×高×2解答。
【解答】解:25×18+25×40×2+18×40×2
=450+2000+1440
=3890(平方厘米)
3890平方厘米=38.9平方分米
答:做这个水桶至少用铁皮38.9平方分米。
【点评】本题主要考查了学生对长方体表面积计算方法的题目。要注意单位的换算。
43.325厘米。
【分析】彩带的总长包括2条长、2条宽、4条高及蝴蝶结的长度,据此解答。
【解答】解:50×2+40×2+30×4+25
=100+80+120+25
=325(厘米)
答:包装这个礼盒需要325厘米的彩带。
【点评】此题主要考查长方体的特征及棱长总和的计算方法。
44.135厘米。
【分析】根据长方体的特征:12条棱分为互相平行的3组,每组4条棱的长度相等,由图形可知:需要彩带的长度等于2条长+4条高+2条宽+打结用的25厘米即可。
【解答】解:20×2+15×2+10×4+25
=40+30+40+25
=135(厘米)
答:至少需要135厘米的彩带。
【点评】此题考查的目的是理解掌握长方体的特征,以及长方体棱长总和的计算方法,结合题意分析解答即可。
45.700。
【分析】根据题意,铁皮的面积=长方形面积﹣四个小正方形面积,据此解答。
【解答】解:40×20﹣5×5×4
=800﹣100
=700(平方厘米)
答:做这个铁盒需要700平方厘米铁皮。
【点评】本题考查了长方体的展开图问题,解决本题的关键是将铁皮的面积转化成长方形和正方形的面积。
46.见试题解答内容
【分析】做这个水箱至少需要多少平方分米铁皮,首先明确它无盖,是求它的5个面的总面积,根据长方体的表面积的计算方法解答.
【解答】解:45×30+(30×24+24×45)×2
=1350+(720+1080)×2
=1350+1800×2
=1350+3600
=4950(平方厘米)
答:制作这个水箱至少需要4950平方厘米铁皮.
【点评】这是一道长方体表面积的实际应用,在计算表面积时要分清需要计算几个面的面积,缺少的是哪一个面的面积,从而列式解答即可.
47.12.96平方分米。
【分析】根据正方体的表面积公式:S=6a2,把数据代入公式求出这个礼品盒表面积,再乘上1.5即可解答。
【解答】解:1.2×1.2×6×1.5
=1.44×6×1.5
=8.64×1.5
=12.96(平方分米)
答:至少要用12.96平方分米的包装纸。
【点评】此题主要考查正方体表面积公式的灵活运用,关键是熟记公式。
48.1920平方分米。
【分析】做4节这样的通风管需要铁皮的面积=平均每节铁皮的面积×节数;其中,平均每节铁皮的面积=横截面的周长×长;横截面的周长=横截面的边长×4。
【解答】解:3米=30分米
4×4×30×4
=16×30×4
=480×4
=1920(平方分米)
答:做4节这样的通风管需要1920平方分米铁皮。
【点评】本题考查了长方体的表面积公式的应用。
49.112cm2。
【分析】上下面不贴,就是在左右面和前后面四个面贴上商标纸,求出这四个面的面积和即可。
【解答】解:(9×4+5×4)×2
=(36+20)×2
=56×2
=112(cm2)
答:这张商标纸的面积至少需要112cm2。
【点评】此题考查长方体表面积的实际应用,在计算时要分清需要计算几个长方形面的面积,缺少的是哪些面的面积,从而列式解答即可。
同课章节目录
