人教版五年级数学下册 总复习(长方体和正方体 ) 课件(共20张PPT)
文档属性
| 名称 | 人教版五年级数学下册 总复习(长方体和正方体 ) 课件(共20张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-04-16 00:00:00 | ||
图片预览







文档简介
(共20张PPT)
长方体和正方体
复 习
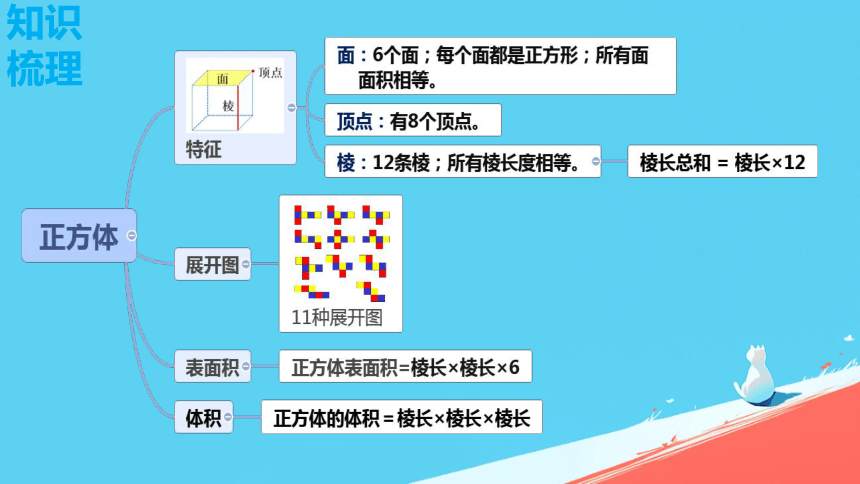
知识梳理
知识梳理
知识梳理
一、认识长方体和正方体的特征及它们的展开图。
二、掌握长方体和正方体表面积的计算方法,并能运用所学知识解决一些简单的实际问题。
三、了解体积的意义及计量单位,会进行单位之间的换算。
四、掌握长方体和正方体体积的计算,并会运用公式解决实际问题。
五、认识容积的意义及计量单位,会进行容积单位和体积单位的互化。
六、测量不规则物体的体积。
目录
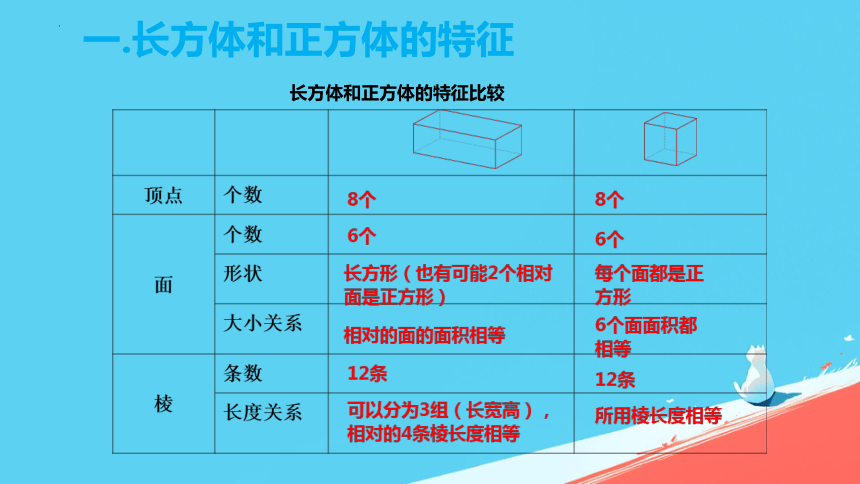
一.长方体和正方体的特征
长方体和正方体的特征比较
下图中哪些是正方体的展开图?
1.节日到了,商店现要用彩带打包一种礼盒(如左图)出售。如果结头处要用掉彩带25cm,打包一个盒子的彩带长多少厘米?
一个盒子的彩带:结头处的彩带长+ 每个面的彩带长度
前后面: 左右面: 上下面:
相当于计算(2)个长、(2)个宽、(4)个高
一个礼盒:2×10+2×15+4×8=82(厘米)
25+82=107(厘米)
(单位:厘米)
2.用下面这些小棒(有多余)和橡皮泥做一个长方体框架。长宽高分别长多少厘米?
答:相交于一个顶点的三条棱分别长6cm、6cm、5cm.
长方体有 条相等的长, 条相等的宽, 条相等的高。
3.有一根长为96厘米的铁丝,如果焊成一个正方体框架,那么这个正方形的棱长是
多少厘米?
96 12=8(cm)
二.长方体、正方体的表面积
4.把一个如下图所示木箱的各面都贴上彩纸,至少需要多少平方厘米的彩纸。
40×25×4+40×40×2=7200(平方分米)
5.做一个如下图的无盖纸盒,至少需要多少平方厘米的纸板?
无盖的正方体的表面积=
棱长×棱长×5
(单位:分米)
(40×25+40×40+40×25)×2=7200(平方分米)
计算公式 (长×宽+长×高+高×宽)×2
6.长8.5米,宽6米,高4.2米的五年级教室要进行重新粉刷。教室门窗和黑板的面积一共有35.8平方米。那么,需要粉刷的面积是多少平方米?
7.将一个由5个棱长是10cm的正方体拼成的长方体拆开,表面积增加了多少?5个正方体的表面积之和是多少?
表面积有什么变化?增加几个面
增加的面积 10×10×8=800(平方厘米)
方法一
方法二
求出一个小正方体的表面积×5
10×10×6×5=3000(平方厘米)
求出长方体的表面积+增加的面积
50×10×4+10×10×2+10×10×8=3000(平方厘米)
三.体积意义、单位
常用的体积单位有立方厘米、立方分米和立方米,可以分别写成cm3、dm3、m3。
1立方分米=1000立方厘米
1立方米=1000立方分米
相邻的两个体积单位间的进率是1000
在同类的计量单位中,较大的单位叫高级单位,较小的单位叫低级单位,高级单位和低级单位是
相对而言的。由高级单位换算成低级单位,要乘进率;由低级单位换算成高级单位,要除以进率。
4.09立方米=( )立方分米 560立方厘米=( )立方分米
340平方分米=( )平方米 5.6平方分米=( )平方厘米
四、体积
8.将一个棱长6cm正方体重新铸成长一个宽8cm、高3cm的长方体铁块,这个正方体的体积是多少?长方体的长是多少厘米?
什么没有变?
五、容积
容积单位的换算:1升=1000毫升
容积单位和体积单位的关系:1升=1立方分米 1毫升=1立方厘米
长方体或正方体容器容积的计算方法跟体积的计算方法相同。
9.一个长方体水池,底面长12dm,宽6dm。如果要向这个池子里注入2dm高的水,需要多少升水?后面丢一个石头进去,水面高度变为2.2dm,石头的体积是多少?
12×6×2=144(dm3)
144(dm3)=144(升)
2.2-2=0.2(dm)
12×6×0.2=14.4(dm3)
水面上升的那部分水的体积就是石头的体积。
六、不规则物体体积
用排水法测量不规则物体的体积时,不规则物体必须完全浸入水中,才能测量。
1.用一根铁丝可以制成一个棱长是6cm正方体框架,如果改制成一个宽为6厘米,高为3厘米长方体框架,这个长方体框架的棱长是多少厘米?
长方体的高=棱长总和 4-长-宽
铁丝长度 正方体棱长和 12 6=72(cm)
6 4=24(cm)
3 4=12(cm)
(72-24-12) 4
=36 4
=9(cm)
4条长方体的长=棱长总和-4条高-4条宽
2.小丽想给买的长方体专辑缝个外罩,长31厘米,宽27厘米,高2.5厘米,封套的左面不封口做这个外罩至少需要多少平方厘米布?
=1886.5cm2
一、(1)用铁丝焊一个棱长总和是36cm的正方体框架,那么它棱长都是6cm。( )
(2)如果两个物体的体积相等,那么它们的形状也相同( )
(3)用四个大小相同的小正方体可以拼成一个大正方体( )
(4)正方体的棱长扩大到原来的3倍,体积扩大27倍。( )
(5)把一块正方体的橡皮泥捏成长方体,体积不变。( )
二、
七、作业
三、汽车油箱的容积大约是72( )。数学书的体积大约是320( )。
小结
通过整理、复习,我们再次熟悉了......收获了......
我再次复习了长方体和正方体的特征,表面积......
长方体和正方体
复 习
知识梳理
知识梳理
知识梳理
一、认识长方体和正方体的特征及它们的展开图。
二、掌握长方体和正方体表面积的计算方法,并能运用所学知识解决一些简单的实际问题。
三、了解体积的意义及计量单位,会进行单位之间的换算。
四、掌握长方体和正方体体积的计算,并会运用公式解决实际问题。
五、认识容积的意义及计量单位,会进行容积单位和体积单位的互化。
六、测量不规则物体的体积。
目录
一.长方体和正方体的特征
长方体和正方体的特征比较
下图中哪些是正方体的展开图?
1.节日到了,商店现要用彩带打包一种礼盒(如左图)出售。如果结头处要用掉彩带25cm,打包一个盒子的彩带长多少厘米?
一个盒子的彩带:结头处的彩带长+ 每个面的彩带长度
前后面: 左右面: 上下面:
相当于计算(2)个长、(2)个宽、(4)个高
一个礼盒:2×10+2×15+4×8=82(厘米)
25+82=107(厘米)
(单位:厘米)
2.用下面这些小棒(有多余)和橡皮泥做一个长方体框架。长宽高分别长多少厘米?
答:相交于一个顶点的三条棱分别长6cm、6cm、5cm.
长方体有 条相等的长, 条相等的宽, 条相等的高。
3.有一根长为96厘米的铁丝,如果焊成一个正方体框架,那么这个正方形的棱长是
多少厘米?
96 12=8(cm)
二.长方体、正方体的表面积
4.把一个如下图所示木箱的各面都贴上彩纸,至少需要多少平方厘米的彩纸。
40×25×4+40×40×2=7200(平方分米)
5.做一个如下图的无盖纸盒,至少需要多少平方厘米的纸板?
无盖的正方体的表面积=
棱长×棱长×5
(单位:分米)
(40×25+40×40+40×25)×2=7200(平方分米)
计算公式 (长×宽+长×高+高×宽)×2
6.长8.5米,宽6米,高4.2米的五年级教室要进行重新粉刷。教室门窗和黑板的面积一共有35.8平方米。那么,需要粉刷的面积是多少平方米?
7.将一个由5个棱长是10cm的正方体拼成的长方体拆开,表面积增加了多少?5个正方体的表面积之和是多少?
表面积有什么变化?增加几个面
增加的面积 10×10×8=800(平方厘米)
方法一
方法二
求出一个小正方体的表面积×5
10×10×6×5=3000(平方厘米)
求出长方体的表面积+增加的面积
50×10×4+10×10×2+10×10×8=3000(平方厘米)
三.体积意义、单位
常用的体积单位有立方厘米、立方分米和立方米,可以分别写成cm3、dm3、m3。
1立方分米=1000立方厘米
1立方米=1000立方分米
相邻的两个体积单位间的进率是1000
在同类的计量单位中,较大的单位叫高级单位,较小的单位叫低级单位,高级单位和低级单位是
相对而言的。由高级单位换算成低级单位,要乘进率;由低级单位换算成高级单位,要除以进率。
4.09立方米=( )立方分米 560立方厘米=( )立方分米
340平方分米=( )平方米 5.6平方分米=( )平方厘米
四、体积
8.将一个棱长6cm正方体重新铸成长一个宽8cm、高3cm的长方体铁块,这个正方体的体积是多少?长方体的长是多少厘米?
什么没有变?
五、容积
容积单位的换算:1升=1000毫升
容积单位和体积单位的关系:1升=1立方分米 1毫升=1立方厘米
长方体或正方体容器容积的计算方法跟体积的计算方法相同。
9.一个长方体水池,底面长12dm,宽6dm。如果要向这个池子里注入2dm高的水,需要多少升水?后面丢一个石头进去,水面高度变为2.2dm,石头的体积是多少?
12×6×2=144(dm3)
144(dm3)=144(升)
2.2-2=0.2(dm)
12×6×0.2=14.4(dm3)
水面上升的那部分水的体积就是石头的体积。
六、不规则物体体积
用排水法测量不规则物体的体积时,不规则物体必须完全浸入水中,才能测量。
1.用一根铁丝可以制成一个棱长是6cm正方体框架,如果改制成一个宽为6厘米,高为3厘米长方体框架,这个长方体框架的棱长是多少厘米?
长方体的高=棱长总和 4-长-宽
铁丝长度 正方体棱长和 12 6=72(cm)
6 4=24(cm)
3 4=12(cm)
(72-24-12) 4
=36 4
=9(cm)
4条长方体的长=棱长总和-4条高-4条宽
2.小丽想给买的长方体专辑缝个外罩,长31厘米,宽27厘米,高2.5厘米,封套的左面不封口做这个外罩至少需要多少平方厘米布?
=1886.5cm2
一、(1)用铁丝焊一个棱长总和是36cm的正方体框架,那么它棱长都是6cm。( )
(2)如果两个物体的体积相等,那么它们的形状也相同( )
(3)用四个大小相同的小正方体可以拼成一个大正方体( )
(4)正方体的棱长扩大到原来的3倍,体积扩大27倍。( )
(5)把一块正方体的橡皮泥捏成长方体,体积不变。( )
二、
七、作业
三、汽车油箱的容积大约是72( )。数学书的体积大约是320( )。
小结
通过整理、复习,我们再次熟悉了......收获了......
我再次复习了长方体和正方体的特征,表面积......
