2024年辽宁中考数学二轮中考考点研究 2.1 一次方程(组)及其应用 课件(共38张PPT)
文档属性
| 名称 | 2024年辽宁中考数学二轮中考考点研究 2.1 一次方程(组)及其应用 课件(共38张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 235.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-04-16 17:17:11 | ||
图片预览





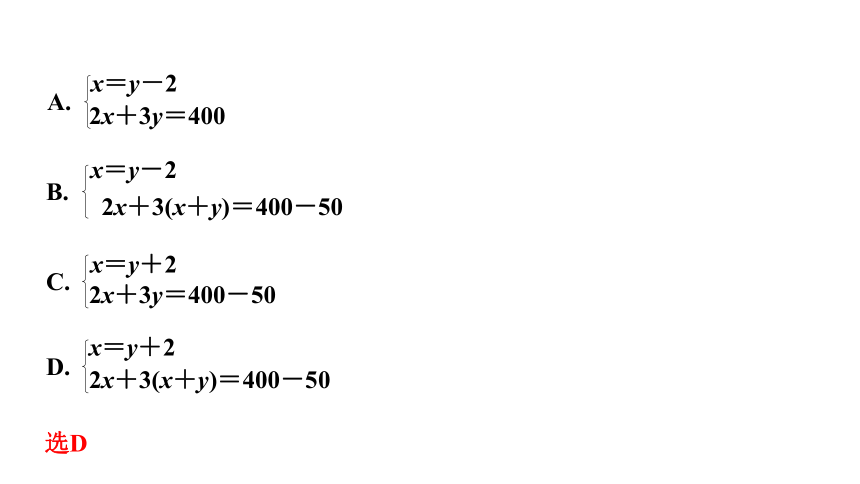






文档简介
(共38张PPT)
第一节 一次方程(组)及其应用
辽宁近年中考真题精选
1
考点精讲
2
重难点分层练
3
辽宁近年中考真题精选
1
命题点
方程组的解法及解的应用(沈阳2考;铁岭2023.14)
1. (2020沈阳12题3分)二元一次方程组 的解是________.
x+y=5
2x-y=1
x=2
y=3
2. (2023铁岭14题3分)若x,y满足方程组 ,则x+y=________.
3x+y=17
x-y=3
7
辽宁其他地市真题
3. (2020朝阳13题3分)已知关于x、y的方程组 的解满足x+y=-3,则a的值为________.
2x+y=2a+1
x+2y=5-5a
5
2
命题点
一次方程(组)的实际应用
4. (2020铁岭葫芦岛7题3分)我市在落实国家“精准扶贫”政策的过程中,为某村修建一条长为400米的公路,由甲、乙两个工程队负责施工.甲工程队独立施工2天后,乙工程队加入,两工程队联合施工3天后,还剩下50米的工程.已知甲工程队每天比乙工程队多施工2米,求甲、乙工程队每天各施工多少米?设甲工程队每天施工x米,乙工程队每天施工y米,根据题意,所列方程组正确的是( )
A.
x=y-2
2x+3y=400
B.
D.
C.
x=y-2
2x+3(x+y)=400-50
x=y+2
2x+3y=400-50
x=y+2
2x+3(x+y)=400-50
选D
5. (2022本溪8题3分)为了美化校园,学校计划购买甲、乙两种花木共200棵进行绿化,其中甲种花木每棵80元,乙种花木每棵100元,若购买甲、乙两种花木共花费17600元,求学校购买甲、乙两种花木各多少棵?设购买甲种花木x棵,乙种花木y棵,根据题意列出的方程组正确的是( )
x+y=200
A.
80x+100y=17600
B.
x+y=200
100x+80y=17600
C.
x+y=17600
+ =200
D.
x+y=17600
+ =200
A
辽宁其他地市真题
6. (2023鞍山6题3分)某班有若干个活动小组,其中书法小组人数的3倍比绘画小组的人数多15人,绘画小组人数的2倍比书法小组的人数多5人,问:书法小组和绘画小组各有多少人?若设书法小组有x人,绘画小组有y人,那么可列方程组为( )
A.
y-3x=15
x-2y=5
B.
y-3x=15
2y-x=5
C.
3x-y=15
x-2y=5
D.
3x-y=15
2y-x=5
D
7. (2022大连14题3分)《孙子算经》中记载了一道题,大意是:100匹马恰好拉了100片瓦,已知1匹大马能拉3片瓦,3匹小马能拉1片瓦,问有多少匹大马、多少匹小马?设有x匹大马,y匹小马,根据题意可
列方程组为______________.
8.有一个运输队承包了一家公司运送货物的业务,第一次运送18 t,派了一辆大卡车和5辆小卡车;第二次运送38 t,派了两辆大卡车和11辆小卡车,并且两次派的车都刚好装满.
(1)两种车型的载重量各是多少?
解:(1)设大卡车的载重量为x吨,小卡车的载重量为y吨,
根据题意得:
解得:
答:大卡车的载重量为8吨,小卡车的载重量为2吨.
(2)若大卡车运送一次的费用为200元,小卡车运送一次的费用为60元,在第一次运送过程中怎样安排大小车辆,才能使费用最少?(直接写出派车方案)
(2)设安排m辆大卡车,运费为w元,则应安排 =(9﹣4m)辆小卡车,
依题意得:w=200m+60(9﹣4m)=﹣40m+540,
∵k=﹣40<0,
∴w随m值的增大而减小.
∵9﹣4m,m均为非负整数,
∴m可以取0,1,2,
∴当m=2时,w取得最小值,此时9﹣4m=1,
∴安排2辆大卡车1辆小卡车,才能使费用最少.
等式的
基本性质
解一元一次
方程的步骤
二元一次
方程组及
其解法
代入消元法
加减消元法
一次方程(组)
的实际应用
列方程(组)解应用
题的一般步骤
常见类型及关系式
一次方程
(组)及其应用
考点精讲
【对接教材】北师:七上第五章P129~P153,
八上第五章P102~P134;
人教:七上第三章P77~P112,
七下第八章P87~P112.
等式的基本性质
如果a=b,那么a±c= ________ 移项
如果a=b,那么ac=___________ 去分母
如果a=b(c≠0),那么________= 系数化为1
解一元一次 方程的步骤
1.去分母:结合方程两边都乘以各分母的__________,注意不要漏乘不含分母的项
2.去括号:注意括号前是负号时,去括号后括号内各项均要变号
3.移项:注意移项要变号
4.合并同类项:把方程化成ax=-b(a,b为常数,a≠0)的形式
5.系数化为1:在方程两边都除以未知数的________ ,得到方程的解为x=
b±c
bc
最小公倍数
系数
二元一次方程组及其解法
解法 适用情况 举例
代入消元法 方程组中某一个未知数的系数是1或-1
一个方程的常数项为0
加减消元法 方程组中相同未知数的系数的绝对值相等或成整数倍
相同未知数的系数不同也不互为相反数时,找最 小公倍数
x+3y=7
3x-2y=-1
或
4x-3y=1
3x+2y=8
2x-4y=0
4x-3y=6
9x+2y=15
或
7x-3y=5
3x+2y=5
4x+4y=8
2x+3y=7
3x-2y=4
一次方程(组) 的实际应用
列方程(组) 解应用题的 一般步骤
常见类型及关系式
审:审清题意,明确已知量、未知量,找出两者之间的等量关系
设:选择一个适当的未知数用字母表示,注意带单位
列:根据等量关系,列出方程(组)
解:解所列方程(组),求出未知数的值
验:是否符合实际情况
答:规范作答,注意单位名称
1.利润问题:售价=标价×折扣;销售额=售价×销量;
利润=售价-进价
2.工程问题:工作总量=工作效率×工作时间
3.行程问题:路程=速度×时间
重难点分层练
回顾必备知识
例1 解方程组
x+2y=8①
2x-y=1②
解法一:用代入消元法解方程组(消去y);
解:由②得:________③,
一、解二元一次方程组
y=2x-1
把③代入①得:__________=8,
解得x=________,
把x=2代入③得:y=________,
则方程组的解为________.
解法二:用代入消元法解方程组(消去x),请学生自己完成.
x+2(2x-1)
2
3
解:由①得:x=8-2y③,
把③代入②得:2(8-2y)-y=1,
解得y=3,
把y=3代入③得:x=2,
则方程组的解为
●
易错警示
代入消元法解二元一次方程组,代入后的式子较为复杂,运算过程易出现错误.
解法三:用加减消元法解方程组(消去y);
解:②×2得:__________③,
①+③得:________,
解得x=________,
把x=2代入②得:y=________,
则方程组的解为________.
解法四:用加减消元法解方程组(消去x),请学生自己完成.
4x-2y=2
5x=10
2
3
解:①×2得:2x+4y=16③,
③-②得:5y=15,
解得y=3,
把y=3代入①得:x=2,
则方程组的解为
●
易错警示
加减消元法解二元一次方程组,用减法消元时,产生负号问题,运算过程易出现错误;用加法消元法时,运算简单,不易出错.
满分技法
在解二元一次方程组时,优先选择加法消元法,其次选择减法消元法最后选择代入消元法
体验辽宁考法
1. 已知方程组 ,则x-y的值是( )
A. 1 B. 2 C. 4 D. 5
2x+3y=14
x+4y=12
B
例2 填空:
(1)①一本笔记本是x元,一支圆珠笔是y元,则买4本笔记本和2支圆珠笔共需________元.
基本关系式:总价=单价×数量;
转换关系式:总价=笔记本单价×数量+圆珠笔单价×数量.
(4x+2y)
回顾必备知识
二、一次方程(组)的实际应用
③某款服装一件的进价为200元,标价为x元,若按标价的八折销售,则售价为________元,仍可获利20%,则可列方程______________
___________.
0.8x-200=
0.8x
200×20%
基本关系式:售价=标价×折扣;
转换关系式:___________________________________________.
售价=牛奶标价×八折
②已知商店里牛奶每箱标价a元.第一次降价打“八折”,则第一次打折后的售价是______元,第二次降价每件又减5元,则第二次降价后的售价是________元.
0.8a
(0.8a-5)
基本关系式:_______________________________________________;
转换关系式:_________________________.
利润=售价-进价
利润=标价×折扣-进价
(2)小明沿一条直路走了3千米后,再以4千米/小时的速度继续往前走了t小时,那么小明共走了________千米.
基本关系式:________________________________________________;
转换关系式:________________________________________________.
(3+4t)
路程=速度×时间
路程=先走路程+后走路程=先走路程+速度×时间
(3)一条地下管线由甲工程队单独铺设需要12天,则甲工程队每天完成总工程量的________,要由乙工程队单独铺设需要24天,则乙工程队每天完成总工程量的________,如果由甲、乙两个工程队从两端同时施工,设要用x天可以铺好这条管线,则可列方程____________.
基本关系式:_______________________________________________;
转换关系式:________________________________________________
_________________.
工作总量=工作效率×工作时间
工作总量=甲工作效率×甲的工作时间+乙工作效率×
乙的工作时间
例3 为提高居民满意度,某小区物业对①面积为3600平方米的区域进行了绿化,整项工程甲先施工,后因有其他任务,由乙工程队接手完成,②甲队每天绿化200平方米,③乙队每天绿化160平方米,④两队共用21天.求⑤甲、乙两队在这项绿化工程中分别工作了多少天.
提升关键能力
【基本关系式】
本题属于工作总量问题基本关系式:
工作总量=工作效率×工作时间
【分层分析】
【解法一】第一步:读完题,先看设问;
怎么设?看设问⑤,设甲队工作了x天,乙队工作了y天.
第二步:转化题干信息:
a.根据信息④,利用“总工作时间=甲工作时间+乙工作时间”可得___________;
b.根据信息①,结合基本关系式,可得转换关系式为_____________
_________________________________;
c.从信息②和③可得甲、乙工作效率,再将其与甲、乙的工作时间代入转化后的关系式从题干信息④可列方程____________________.
第三步:解方程及作答
求得x及y的值作答即可.
x+y=21
工作总量=甲队工作量+乙队工作量
200x+160y=3600
【解法一】
解:设甲队工作了x天,乙队工作了y天,
依题意得 ,
解得 .
答:甲队工作了6天,乙队工作了15天.
【解法二】 第一步:读完题,先看设问;
(1)先设1个:设甲队工作了x天;
第二步:转化题干信息:
a.根据信息④及假设条件,可得乙队工作时间为_______天;
b.根据信息①,结合基本关系式,可得转换关系式为_____________________________________________________;
c.从信息②和③可得甲、乙工作效率,再将其与甲、乙的工作时间代入转化后的关系式从题干信息④可列方程______________________.
(21-x)
工作总量=甲队工作量+乙队工作量
200x+160(21-x)=3600
【解法二】
解:设甲队工作了x天,乙队工作了(21-x)天,依题意,得
200x+160(21-x)=3600,
解得x=6,
∴乙队工作了21-6=15天
答:甲队工作了6天,乙队工作了15天.
第三步:解方程及作答
求得x及y的值作答即可.
体验辽宁考法
2. 小明的妈妈在菜市场买回2斤萝卜、1斤排骨共花了39元,而两个月前买同重量的这两样菜要45元,与两个月前相比,这次萝卜的单价上涨了10%,但排骨的单价却下跌了20%,求:两个月前买的萝卜和排骨的单价分别为多少元?
解:设两个月前买的萝卜的单价为x元,排骨的单价为y元,
依题意得
解得 .
答:两个月前买的萝卜的单价为5元,排骨的单价为35元.
第一节 一次方程(组)及其应用
辽宁近年中考真题精选
1
考点精讲
2
重难点分层练
3
辽宁近年中考真题精选
1
命题点
方程组的解法及解的应用(沈阳2考;铁岭2023.14)
1. (2020沈阳12题3分)二元一次方程组 的解是________.
x+y=5
2x-y=1
x=2
y=3
2. (2023铁岭14题3分)若x,y满足方程组 ,则x+y=________.
3x+y=17
x-y=3
7
辽宁其他地市真题
3. (2020朝阳13题3分)已知关于x、y的方程组 的解满足x+y=-3,则a的值为________.
2x+y=2a+1
x+2y=5-5a
5
2
命题点
一次方程(组)的实际应用
4. (2020铁岭葫芦岛7题3分)我市在落实国家“精准扶贫”政策的过程中,为某村修建一条长为400米的公路,由甲、乙两个工程队负责施工.甲工程队独立施工2天后,乙工程队加入,两工程队联合施工3天后,还剩下50米的工程.已知甲工程队每天比乙工程队多施工2米,求甲、乙工程队每天各施工多少米?设甲工程队每天施工x米,乙工程队每天施工y米,根据题意,所列方程组正确的是( )
A.
x=y-2
2x+3y=400
B.
D.
C.
x=y-2
2x+3(x+y)=400-50
x=y+2
2x+3y=400-50
x=y+2
2x+3(x+y)=400-50
选D
5. (2022本溪8题3分)为了美化校园,学校计划购买甲、乙两种花木共200棵进行绿化,其中甲种花木每棵80元,乙种花木每棵100元,若购买甲、乙两种花木共花费17600元,求学校购买甲、乙两种花木各多少棵?设购买甲种花木x棵,乙种花木y棵,根据题意列出的方程组正确的是( )
x+y=200
A.
80x+100y=17600
B.
x+y=200
100x+80y=17600
C.
x+y=17600
+ =200
D.
x+y=17600
+ =200
A
辽宁其他地市真题
6. (2023鞍山6题3分)某班有若干个活动小组,其中书法小组人数的3倍比绘画小组的人数多15人,绘画小组人数的2倍比书法小组的人数多5人,问:书法小组和绘画小组各有多少人?若设书法小组有x人,绘画小组有y人,那么可列方程组为( )
A.
y-3x=15
x-2y=5
B.
y-3x=15
2y-x=5
C.
3x-y=15
x-2y=5
D.
3x-y=15
2y-x=5
D
7. (2022大连14题3分)《孙子算经》中记载了一道题,大意是:100匹马恰好拉了100片瓦,已知1匹大马能拉3片瓦,3匹小马能拉1片瓦,问有多少匹大马、多少匹小马?设有x匹大马,y匹小马,根据题意可
列方程组为______________.
8.有一个运输队承包了一家公司运送货物的业务,第一次运送18 t,派了一辆大卡车和5辆小卡车;第二次运送38 t,派了两辆大卡车和11辆小卡车,并且两次派的车都刚好装满.
(1)两种车型的载重量各是多少?
解:(1)设大卡车的载重量为x吨,小卡车的载重量为y吨,
根据题意得:
解得:
答:大卡车的载重量为8吨,小卡车的载重量为2吨.
(2)若大卡车运送一次的费用为200元,小卡车运送一次的费用为60元,在第一次运送过程中怎样安排大小车辆,才能使费用最少?(直接写出派车方案)
(2)设安排m辆大卡车,运费为w元,则应安排 =(9﹣4m)辆小卡车,
依题意得:w=200m+60(9﹣4m)=﹣40m+540,
∵k=﹣40<0,
∴w随m值的增大而减小.
∵9﹣4m,m均为非负整数,
∴m可以取0,1,2,
∴当m=2时,w取得最小值,此时9﹣4m=1,
∴安排2辆大卡车1辆小卡车,才能使费用最少.
等式的
基本性质
解一元一次
方程的步骤
二元一次
方程组及
其解法
代入消元法
加减消元法
一次方程(组)
的实际应用
列方程(组)解应用
题的一般步骤
常见类型及关系式
一次方程
(组)及其应用
考点精讲
【对接教材】北师:七上第五章P129~P153,
八上第五章P102~P134;
人教:七上第三章P77~P112,
七下第八章P87~P112.
等式的基本性质
如果a=b,那么a±c= ________ 移项
如果a=b,那么ac=___________ 去分母
如果a=b(c≠0),那么________= 系数化为1
解一元一次 方程的步骤
1.去分母:结合方程两边都乘以各分母的__________,注意不要漏乘不含分母的项
2.去括号:注意括号前是负号时,去括号后括号内各项均要变号
3.移项:注意移项要变号
4.合并同类项:把方程化成ax=-b(a,b为常数,a≠0)的形式
5.系数化为1:在方程两边都除以未知数的________ ,得到方程的解为x=
b±c
bc
最小公倍数
系数
二元一次方程组及其解法
解法 适用情况 举例
代入消元法 方程组中某一个未知数的系数是1或-1
一个方程的常数项为0
加减消元法 方程组中相同未知数的系数的绝对值相等或成整数倍
相同未知数的系数不同也不互为相反数时,找最 小公倍数
x+3y=7
3x-2y=-1
或
4x-3y=1
3x+2y=8
2x-4y=0
4x-3y=6
9x+2y=15
或
7x-3y=5
3x+2y=5
4x+4y=8
2x+3y=7
3x-2y=4
一次方程(组) 的实际应用
列方程(组) 解应用题的 一般步骤
常见类型及关系式
审:审清题意,明确已知量、未知量,找出两者之间的等量关系
设:选择一个适当的未知数用字母表示,注意带单位
列:根据等量关系,列出方程(组)
解:解所列方程(组),求出未知数的值
验:是否符合实际情况
答:规范作答,注意单位名称
1.利润问题:售价=标价×折扣;销售额=售价×销量;
利润=售价-进价
2.工程问题:工作总量=工作效率×工作时间
3.行程问题:路程=速度×时间
重难点分层练
回顾必备知识
例1 解方程组
x+2y=8①
2x-y=1②
解法一:用代入消元法解方程组(消去y);
解:由②得:________③,
一、解二元一次方程组
y=2x-1
把③代入①得:__________=8,
解得x=________,
把x=2代入③得:y=________,
则方程组的解为________.
解法二:用代入消元法解方程组(消去x),请学生自己完成.
x+2(2x-1)
2
3
解:由①得:x=8-2y③,
把③代入②得:2(8-2y)-y=1,
解得y=3,
把y=3代入③得:x=2,
则方程组的解为
●
易错警示
代入消元法解二元一次方程组,代入后的式子较为复杂,运算过程易出现错误.
解法三:用加减消元法解方程组(消去y);
解:②×2得:__________③,
①+③得:________,
解得x=________,
把x=2代入②得:y=________,
则方程组的解为________.
解法四:用加减消元法解方程组(消去x),请学生自己完成.
4x-2y=2
5x=10
2
3
解:①×2得:2x+4y=16③,
③-②得:5y=15,
解得y=3,
把y=3代入①得:x=2,
则方程组的解为
●
易错警示
加减消元法解二元一次方程组,用减法消元时,产生负号问题,运算过程易出现错误;用加法消元法时,运算简单,不易出错.
满分技法
在解二元一次方程组时,优先选择加法消元法,其次选择减法消元法最后选择代入消元法
体验辽宁考法
1. 已知方程组 ,则x-y的值是( )
A. 1 B. 2 C. 4 D. 5
2x+3y=14
x+4y=12
B
例2 填空:
(1)①一本笔记本是x元,一支圆珠笔是y元,则买4本笔记本和2支圆珠笔共需________元.
基本关系式:总价=单价×数量;
转换关系式:总价=笔记本单价×数量+圆珠笔单价×数量.
(4x+2y)
回顾必备知识
二、一次方程(组)的实际应用
③某款服装一件的进价为200元,标价为x元,若按标价的八折销售,则售价为________元,仍可获利20%,则可列方程______________
___________.
0.8x-200=
0.8x
200×20%
基本关系式:售价=标价×折扣;
转换关系式:___________________________________________.
售价=牛奶标价×八折
②已知商店里牛奶每箱标价a元.第一次降价打“八折”,则第一次打折后的售价是______元,第二次降价每件又减5元,则第二次降价后的售价是________元.
0.8a
(0.8a-5)
基本关系式:_______________________________________________;
转换关系式:_________________________.
利润=售价-进价
利润=标价×折扣-进价
(2)小明沿一条直路走了3千米后,再以4千米/小时的速度继续往前走了t小时,那么小明共走了________千米.
基本关系式:________________________________________________;
转换关系式:________________________________________________.
(3+4t)
路程=速度×时间
路程=先走路程+后走路程=先走路程+速度×时间
(3)一条地下管线由甲工程队单独铺设需要12天,则甲工程队每天完成总工程量的________,要由乙工程队单独铺设需要24天,则乙工程队每天完成总工程量的________,如果由甲、乙两个工程队从两端同时施工,设要用x天可以铺好这条管线,则可列方程____________.
基本关系式:_______________________________________________;
转换关系式:________________________________________________
_________________.
工作总量=工作效率×工作时间
工作总量=甲工作效率×甲的工作时间+乙工作效率×
乙的工作时间
例3 为提高居民满意度,某小区物业对①面积为3600平方米的区域进行了绿化,整项工程甲先施工,后因有其他任务,由乙工程队接手完成,②甲队每天绿化200平方米,③乙队每天绿化160平方米,④两队共用21天.求⑤甲、乙两队在这项绿化工程中分别工作了多少天.
提升关键能力
【基本关系式】
本题属于工作总量问题基本关系式:
工作总量=工作效率×工作时间
【分层分析】
【解法一】第一步:读完题,先看设问;
怎么设?看设问⑤,设甲队工作了x天,乙队工作了y天.
第二步:转化题干信息:
a.根据信息④,利用“总工作时间=甲工作时间+乙工作时间”可得___________;
b.根据信息①,结合基本关系式,可得转换关系式为_____________
_________________________________;
c.从信息②和③可得甲、乙工作效率,再将其与甲、乙的工作时间代入转化后的关系式从题干信息④可列方程____________________.
第三步:解方程及作答
求得x及y的值作答即可.
x+y=21
工作总量=甲队工作量+乙队工作量
200x+160y=3600
【解法一】
解:设甲队工作了x天,乙队工作了y天,
依题意得 ,
解得 .
答:甲队工作了6天,乙队工作了15天.
【解法二】 第一步:读完题,先看设问;
(1)先设1个:设甲队工作了x天;
第二步:转化题干信息:
a.根据信息④及假设条件,可得乙队工作时间为_______天;
b.根据信息①,结合基本关系式,可得转换关系式为_____________________________________________________;
c.从信息②和③可得甲、乙工作效率,再将其与甲、乙的工作时间代入转化后的关系式从题干信息④可列方程______________________.
(21-x)
工作总量=甲队工作量+乙队工作量
200x+160(21-x)=3600
【解法二】
解:设甲队工作了x天,乙队工作了(21-x)天,依题意,得
200x+160(21-x)=3600,
解得x=6,
∴乙队工作了21-6=15天
答:甲队工作了6天,乙队工作了15天.
第三步:解方程及作答
求得x及y的值作答即可.
体验辽宁考法
2. 小明的妈妈在菜市场买回2斤萝卜、1斤排骨共花了39元,而两个月前买同重量的这两样菜要45元,与两个月前相比,这次萝卜的单价上涨了10%,但排骨的单价却下跌了20%,求:两个月前买的萝卜和排骨的单价分别为多少元?
解:设两个月前买的萝卜的单价为x元,排骨的单价为y元,
依题意得
解得 .
答:两个月前买的萝卜的单价为5元,排骨的单价为35元.
同课章节目录
