直线与圆方程的应用
图片预览





文档简介
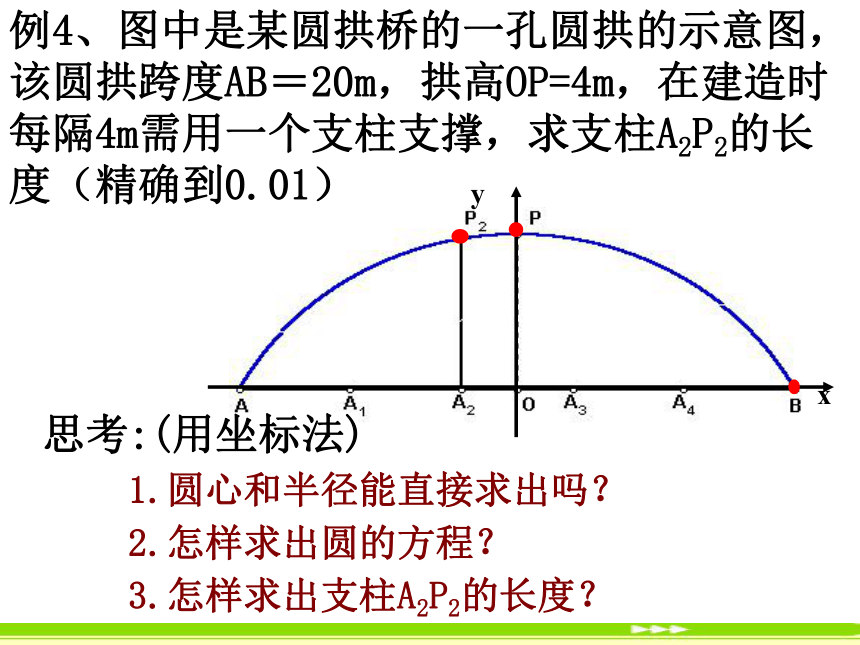
课件24张PPT。§4.2.3直线与圆的方程的应用 例4、图中是某圆拱桥的一孔圆拱的示意图,该圆拱跨度AB=20m,拱高OP=4m,在建造时每隔4m需用一个支柱支撑,求支柱A2P2的长度(精确到0.01)思考:(用坐标法)
1.圆心和半径能直接求出吗?
2.怎样求出圆的方程?
3.怎样求出支柱A2P2的长度?解:建立如图所示的坐标系,设圆心坐标是(0,b),
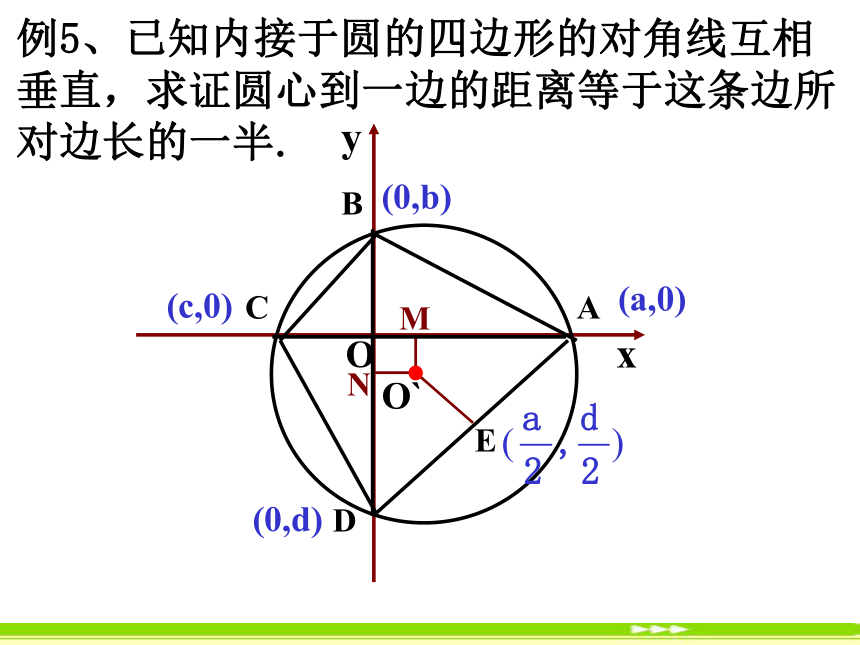
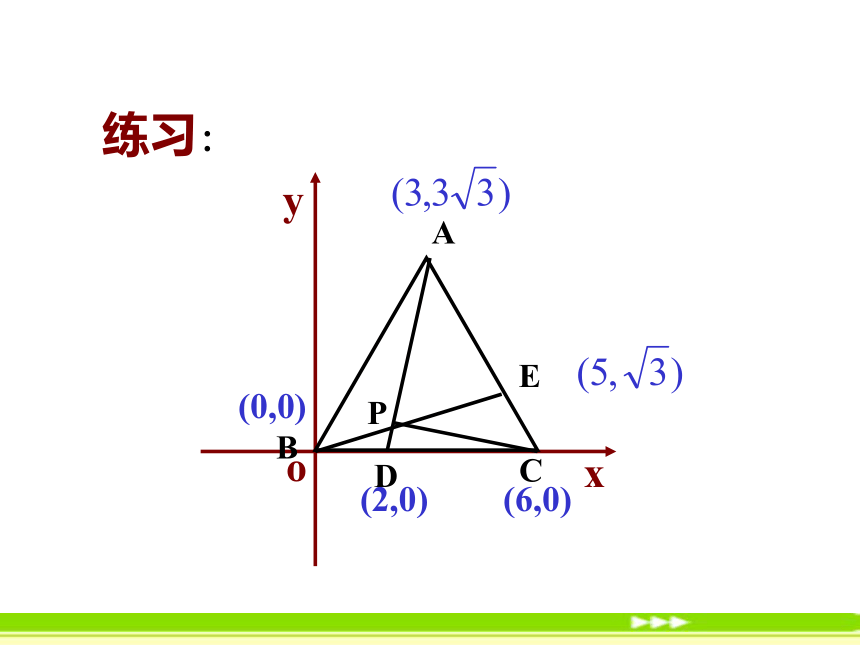
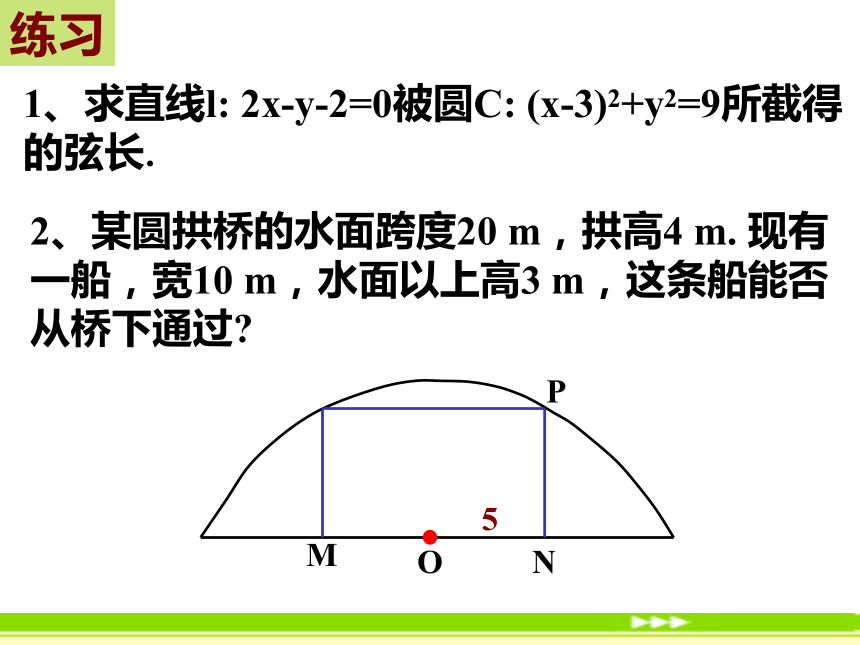
圆的半径是r ,则圆的方程是x2+(y-b)2=r2 .答:支柱A2P2的长度约为3.86m.E例5、已知内接于圆的四边形的对角线互相垂直,求证圆心到一边的距离等于这条边所对边长的一半.(a,0)(0,b)(c,0)(0,d)练习:(6,0)(2,0)(0,0)用坐标法解决平面几何问题的步骤:第一步:建立适当的坐标系,用坐标和方程表示问题中的几何元素,将平面几何问题转化为代数问题;第二步:通过代数运算,解决代数问题;第三步:把代数运算结果“翻译”成几何结论.练习1、求直线l: 2x-y-2=0被圆C: (x-3)2+y2=9所截得的弦长.2、某圆拱桥的水面跨度20 m,拱高4 m. 现有一船,宽10 m,水面以上高3 m,这条船能否从桥下通过?CC练习已知点P(5,0)和⊙O:x2+y2=16
(1)自P作⊙O的切线,求切线的长及切线的方程;
(2)过P任意作直线l与⊙O交于A、B两相异点,求弦AB中点M的轨迹.例题2Q解:(1)设过P的圆O的切线切圆于点Q,∵△PQO是Rt△ ,∴切线长PQ= 连OQ,由题意:消去k得:当y=0时,k=0 此时x=0 而又由 所求轨迹方程为练习(4)若方程 有解,求b的取值范围。 (1)已知圆C:x2+y2-4x-6y+12=0,则过A(3,5)的圆的切线方程为 。(2)圆x2+y2?2x?4y+1=0上到直线x+y?1=0的距离为 的点共有 个。 (3)已知圆C:x2+y2?2x?4y+1=0,直线l:x+y+2=0,在圆上求一点P,使P到直线x+y+2=0的距离最短。设切点为Q(x0,y0),则切线方程为xox+y0y=16由题意得:
所求切线方程为:设所求切线方程为即:设所求切线 方程为:直线l与圆O相切, O到直线l的距离等于半径即:解得:所求切线方程为:例3:试求同时与定直线m和定圆C都相切的动圆圆心的轨迹方程 直线m:x=0,圆C:(x-2)2+y2=4,
动圆圆心轨迹方程为______
y2=8x(x≠0)或y=0(x≠0,x≠2)例5.求过两圆
的交点,且圆心在直线2x-y-4=0上的圆方程。
例3 求过原点及点A(1,1),且在x轴上截得的线段长为3的圆的方程. 分析:设出一般方程,用待定系数法.注意数形结合,由弦长为3可得圆心横坐标为? ,即D = ? 3,可使列方程和解方程组都简便.x2 + y2 +3x ?5y = 0或x2 + y2 ?3x + y = 0也可设标准方程 . 例4 已知圆过点P(2,? 1),与直线x ? y = 1相切,且它的圆心在直线 y = ? 2x上,求这个圆的方程. 分析:本题的条件都与圆心、半径有关,宜选用圆的标准方程,再用待定系数法求出圆心坐标和半径,即得所求圆方程.(x ? 1)2 + ( y + 2)2 = 2,
或(x ? 9)2 + ( y + 18)2 = 338. θ 如图,设⊙O的圆心在原点,半径是r,与x轴正
半轴的交点为P0,圆上任取一点P,若OP0按逆时
针方向旋转到OP位置所形成的角∠P0OP=θ,
求P点的坐标。圆心为(a,b)、半径为r的圆的参数方程为1.圆的参数方程有什么特点?∴ 当sin(θ )=1时,∵ sin(θ ) [-1,1](2)例2. 已知点P(x,y)是圆x2+y2+2x-2 y=0上的一个动点求:(1)x+y的最小值; (2) x2+y2的最大值。 1. 如果直线 l 将圆x2 + y2 ? 2x ? 4y = 0平分,且不通过第四象限,那么l 的斜率的取值范围是( )
A. [0,2] B. [0,1]
C. [0, ] D. ?0, ?思考题A小结 2. 若实数x、y满足等式(x ? 2)2 + y2 = 3,那么 的最大值为( )
A.? B. C. ?D.思考题D小结思考题:3、已知方程
x2 +y2 ?2(t +3)x +2(4t +1)y +18t2 +7= 0.
(1) 当t为何值时,方程表示圆?
(2) 当方程表示圆时,t为何值时, 圆的面积最大? 并求此时的圆的方程. ?1 < t < 3 t = 1, 方程为x2 + y2 ? 8x + 10y + 25 = 0
1.圆心和半径能直接求出吗?
2.怎样求出圆的方程?
3.怎样求出支柱A2P2的长度?解:建立如图所示的坐标系,设圆心坐标是(0,b),
圆的半径是r ,则圆的方程是x2+(y-b)2=r2 .答:支柱A2P2的长度约为3.86m.E例5、已知内接于圆的四边形的对角线互相垂直,求证圆心到一边的距离等于这条边所对边长的一半.(a,0)(0,b)(c,0)(0,d)练习:(6,0)(2,0)(0,0)用坐标法解决平面几何问题的步骤:第一步:建立适当的坐标系,用坐标和方程表示问题中的几何元素,将平面几何问题转化为代数问题;第二步:通过代数运算,解决代数问题;第三步:把代数运算结果“翻译”成几何结论.练习1、求直线l: 2x-y-2=0被圆C: (x-3)2+y2=9所截得的弦长.2、某圆拱桥的水面跨度20 m,拱高4 m. 现有一船,宽10 m,水面以上高3 m,这条船能否从桥下通过?CC练习已知点P(5,0)和⊙O:x2+y2=16
(1)自P作⊙O的切线,求切线的长及切线的方程;
(2)过P任意作直线l与⊙O交于A、B两相异点,求弦AB中点M的轨迹.例题2Q解:(1)设过P的圆O的切线切圆于点Q,∵△PQO是Rt△ ,∴切线长PQ= 连OQ,由题意:消去k得:当y=0时,k=0 此时x=0 而又由 所求轨迹方程为练习(4)若方程 有解,求b的取值范围。 (1)已知圆C:x2+y2-4x-6y+12=0,则过A(3,5)的圆的切线方程为 。(2)圆x2+y2?2x?4y+1=0上到直线x+y?1=0的距离为 的点共有 个。 (3)已知圆C:x2+y2?2x?4y+1=0,直线l:x+y+2=0,在圆上求一点P,使P到直线x+y+2=0的距离最短。设切点为Q(x0,y0),则切线方程为xox+y0y=16由题意得:
所求切线方程为:设所求切线方程为即:设所求切线 方程为:直线l与圆O相切, O到直线l的距离等于半径即:解得:所求切线方程为:例3:试求同时与定直线m和定圆C都相切的动圆圆心的轨迹方程 直线m:x=0,圆C:(x-2)2+y2=4,
动圆圆心轨迹方程为______
y2=8x(x≠0)或y=0(x≠0,x≠2)例5.求过两圆
的交点,且圆心在直线2x-y-4=0上的圆方程。
例3 求过原点及点A(1,1),且在x轴上截得的线段长为3的圆的方程. 分析:设出一般方程,用待定系数法.注意数形结合,由弦长为3可得圆心横坐标为? ,即D = ? 3,可使列方程和解方程组都简便.x2 + y2 +3x ?5y = 0或x2 + y2 ?3x + y = 0也可设标准方程 . 例4 已知圆过点P(2,? 1),与直线x ? y = 1相切,且它的圆心在直线 y = ? 2x上,求这个圆的方程. 分析:本题的条件都与圆心、半径有关,宜选用圆的标准方程,再用待定系数法求出圆心坐标和半径,即得所求圆方程.(x ? 1)2 + ( y + 2)2 = 2,
或(x ? 9)2 + ( y + 18)2 = 338. θ 如图,设⊙O的圆心在原点,半径是r,与x轴正
半轴的交点为P0,圆上任取一点P,若OP0按逆时
针方向旋转到OP位置所形成的角∠P0OP=θ,
求P点的坐标。圆心为(a,b)、半径为r的圆的参数方程为1.圆的参数方程有什么特点?∴ 当sin(θ )=1时,∵ sin(θ ) [-1,1](2)例2. 已知点P(x,y)是圆x2+y2+2x-2 y=0上的一个动点求:(1)x+y的最小值; (2) x2+y2的最大值。 1. 如果直线 l 将圆x2 + y2 ? 2x ? 4y = 0平分,且不通过第四象限,那么l 的斜率的取值范围是( )
A. [0,2] B. [0,1]
C. [0, ] D. ?0, ?思考题A小结 2. 若实数x、y满足等式(x ? 2)2 + y2 = 3,那么 的最大值为( )
A.? B. C. ?D.思考题D小结思考题:3、已知方程
x2 +y2 ?2(t +3)x +2(4t +1)y +18t2 +7= 0.
(1) 当t为何值时,方程表示圆?
(2) 当方程表示圆时,t为何值时, 圆的面积最大? 并求此时的圆的方程. ?1 < t < 3 t = 1, 方程为x2 + y2 ? 8x + 10y + 25 = 0
