江苏省妙桥中学2014-2015学年八年级上数学第五章平面直角坐标系单元测试题及参考答案
文档属性
| 名称 | 江苏省妙桥中学2014-2015学年八年级上数学第五章平面直角坐标系单元测试题及参考答案 |  | |
| 格式 | zip | ||
| 文件大小 | 298.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2015-10-23 17:07:02 | ||
图片预览

文档简介
2014-2015学年第一学期初二数学第五单元测试题
命题:汤志良;审核:杨志刚;分值:130分;知识涵盖:平面直角坐标系.
卷首语:亲爱的同学:在最近这段时间,我们曾付出了辛勤的汗水,今天就让我们尽情采摘成功的果实吧!
一、选择题:(本题共11小题,每小题3分,共33分)
1.(2013.湛江)在平面直角坐标系中,点A(2,-3)在第……………………………( )象限.
A.一; B.二; C.三; D.四;
2.(2013 台湾)坐标平面上有一点A,且A点到轴的距离为3,A点到轴的距离恰为到轴距离的3倍.若A点在第二象限,则A点坐标为何?…………………………( )
A.(-9,3); B.(-3,1); C.(-3,9); D.(-1,3);
3.(2012 深圳)已知点P关于轴的对称点在第一象限,则的取值范围是……………………………………………………………………………………………( )
A.; B.;C.; D.;
4.(2013.遂宁)将点A(3,2)沿轴向左平移4个单位长度得到点A′,点A′关于轴对称的点的坐标是…………………………………………………………………………( )
A.(-3,2); B.(-1,2); C.(1,2); D.(1,-2);
5.(2013 曲靖)在平面直角坐标系中 ( http: / / www.21cnjy.com ),将点P(-2,1)向右平移3个单位长度,再向上平移4个单位长度得到点P′的坐标是………………………………………………………( )
A.(2,4); B.(1,5); C.(1,-3); D.(-5,5);
6.(2014 南安市二模)若点A在轴上,则点B在…………………( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
7.(2014 连云港)在平面直角坐标系内,点P(-2,3)关于原点的对称点Q的坐标为………………( )
A.(2,-3); B.(2,3); C.(3,-2); D.(-2,-3);
8.(2012.荆门)已知点M关于x轴的对称点在第一象限,则的取值范围在数轴上表示正确的是……………………………………………………………( )
9.点N在轴下方、轴左侧,且,,则点N的坐标为…( )
A.(-3,-2);B. (-3,2);C.(3,-2);D.(3,2);
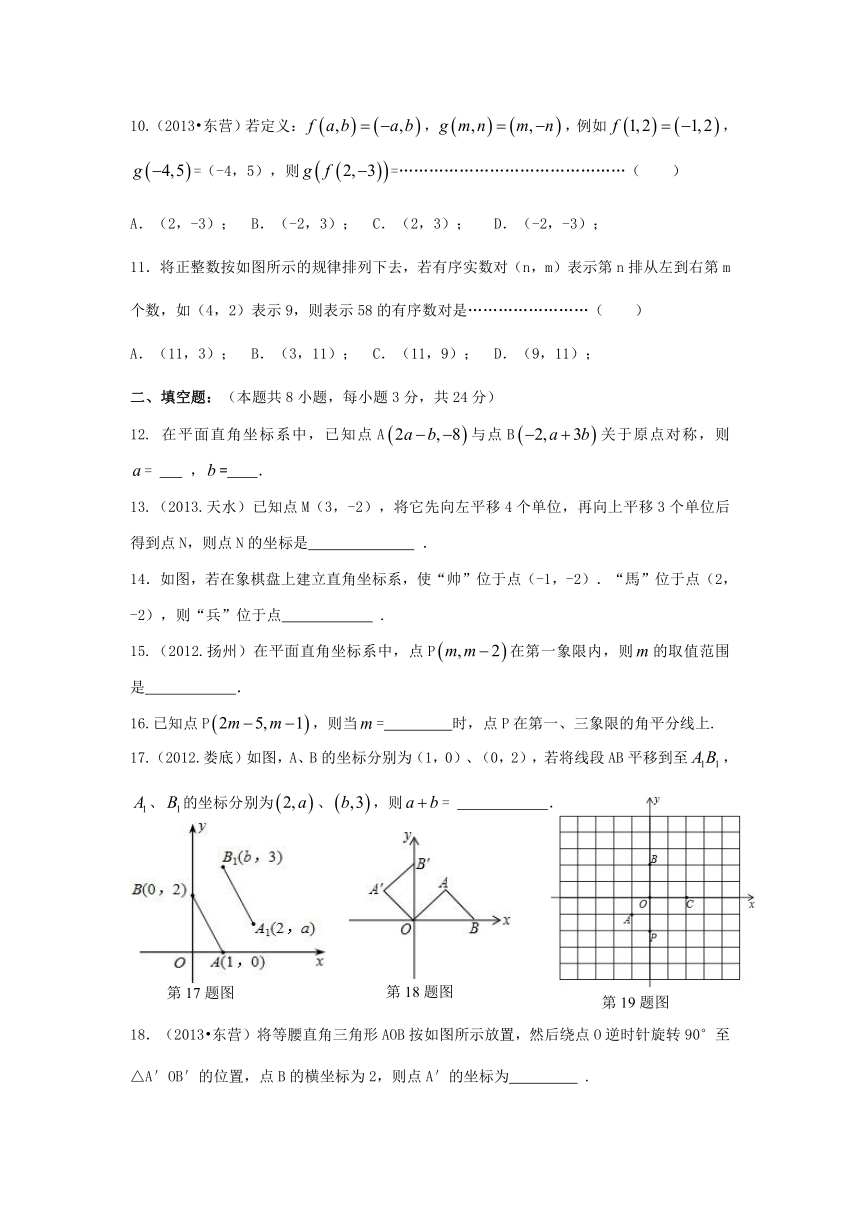
10.(2013 东营)若定义:,,例如,=(-4,5),则=………………………………………( )
A.(2,-3); B.(-2,3); C.(2,3); D.(-2,-3);
11.将正整数按如图所示的规律排列下去,若 ( http: / / www.21cnjy.com )有序实数对(n,m)表示第n排从左到右第m个数,如(4,2)表示9,则表示58的有序数对是……………………( )
A.(11,3); B.(3,11); C.(11,9); D.(9,11);
二、填空题:(本题共8小题,每小题3分,共24分)
12. 在平面直角坐标系中,已知点A与点B关于原点对称,则= ,= .
13.(2013.天水)已知点M(3,-2 ( http: / / www.21cnjy.com )),将它先向左平移4个单位,再向上平移3个单位后得到点N,则点N的坐标是 .
14.如图,若在象棋盘上建立直角坐标系,使“帅”位于点(-1,-2).“馬”位于点(2,-2),则“兵”位于点 .
15.(2012.扬州)在平面直角坐标系中,点P在第一象限内,则的取值范围是 .
16.已知点P,则当= 时,点P在第一、三象限的角平分线上.
17.(2012.娄底)如图,A、B的坐标分别为(1,0)、(0,2),若将线段AB平移到至,、的坐标分别为、,则= .
18.(2013 东营)将 ( http: / / www.21cnjy.com )等腰直角三角形AOB按如图所示放置,然后绕点O逆时针旋转90°至△A′OB′的位置,点B的横坐标为2,则点A′的坐标为 .
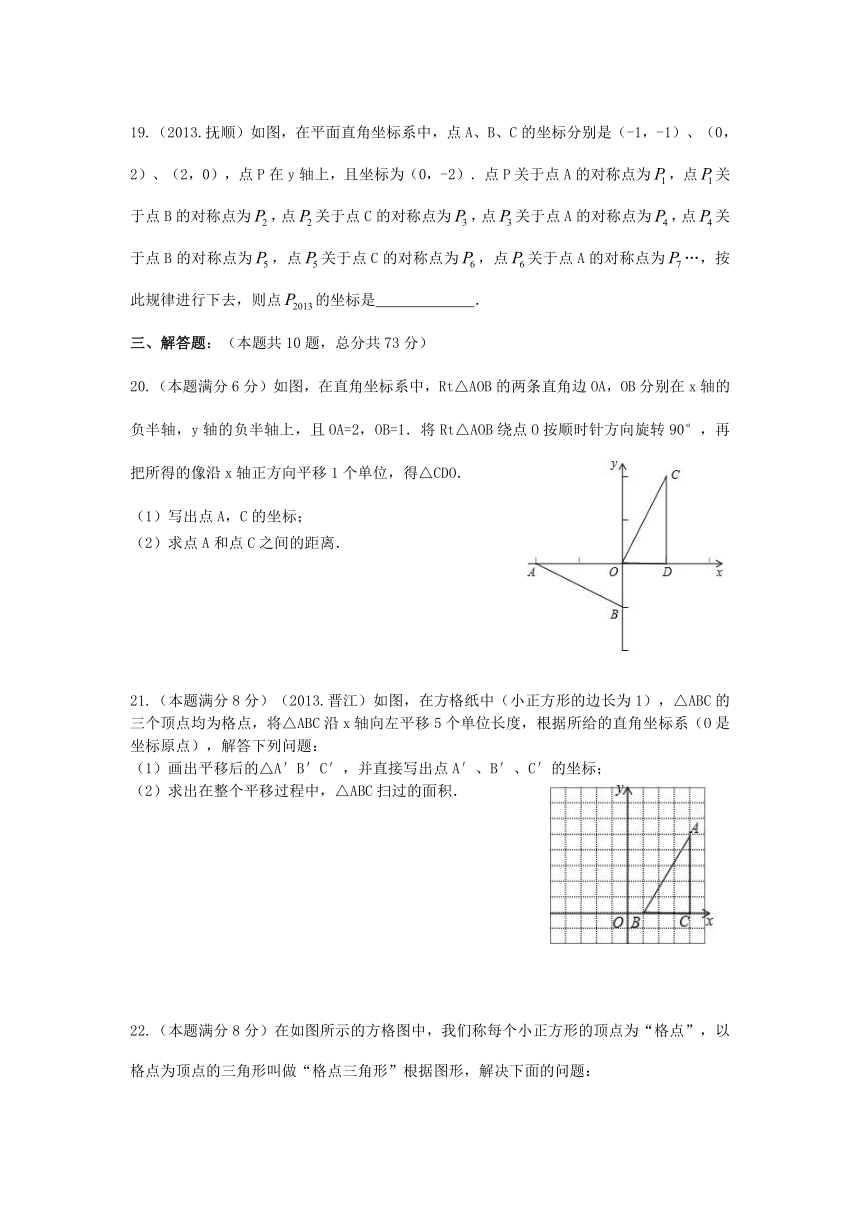
19.(2013.抚顺)如图,在平面直角坐标系中,点A、B、C的坐标分别是(-1,-1)、(0,2)、(2,0),点P在y轴上,且坐标为(0,-2).点P关于点A的对称点为,点关于点B的对称点为,点关于点C的对称点为,点关于点A的对称点为,点关于点B的对称点为,点关于点C的对称点为,点关于点A的对称点为…,按此规律进行下去,则点的坐标是 .
三、解答题:(本题共10题,总分共73分)
20.(本题满分6分)如图,在直角坐标 ( http: / / www.21cnjy.com )系中,Rt△AOB的两条直角边OA,OB分别在x轴的负半轴,y轴的负半轴上,且OA=2,OB=1.将Rt△AOB绕点O按顺时针方向旋转90°,再把所得的像沿x轴正方向平移1个单位,得△CDO.
(1)写出点A,C的坐标;
(2)求点A和点C之间的距离.
21.(本题满分8分)(2013. ( http: / / www.21cnjy.com )晋江)如图,在方格纸中(小正方形的边长为1),△ABC的三个顶点均为格点,将△ABC沿x轴向左平移5个单位长度,根据所给的直角坐标系(O是坐标原点),解答下列问题:
(1)画出平移后的△A′B′C′,并直接写出点A′、B′、C′的坐标;
(2)求出在整个平移过程中,△ABC扫过的面积.
22.(本题满分8分)在如图所示的 ( http: / / www.21cnjy.com )方格图中,我们称每个小正方形的顶点为“格点”,以格点为顶点的三角形叫做“格点三角形”根据图形,解决下面的问题:
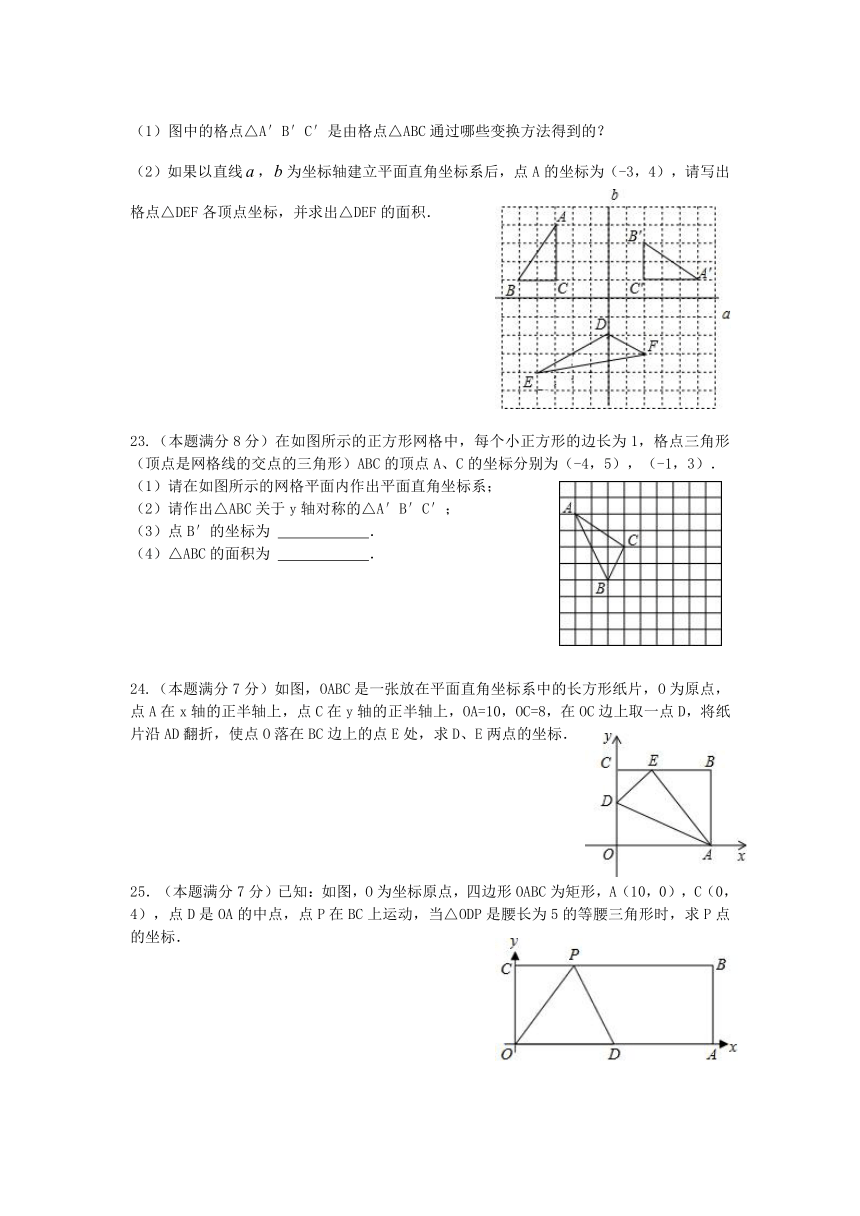
(1)图中的格点△A′B′C′是由格点△ABC通过哪些变换方法得到的?
(2)如果以直线,为坐标轴建立平面直角坐标系后,点A的坐标为(-3,4),请写出格点△DEF各顶点坐标,并求出△DEF的面积.
23.(本题满分8分)在如图所示的正方形网格 ( http: / / www.21cnjy.com )中,每个小正方形的边长为1,格点三角形(顶点是网格线的交点的三角形)ABC的顶点A、C的坐标分别为(-4,5),(-1,3).
(1)请在如图所示的网格平面内作出平面直角坐标系;
(2)请作出△ABC关于y轴对称的△A′B′C′;
(3)点B′的坐标为 .
(4)△ABC的面积为 .
24.(本题满分7分)如图 ( http: / / www.21cnjy.com ),OABC是一张放在平面直角坐标系中的长方形纸片,O为原点,点A在x轴的正半轴上,点C在y轴的正半轴上,OA=10,OC=8,在OC边上取一点D,将纸片沿AD翻折,使点O落在BC边上的点E处,求D、E两点的坐标.
25.(本题满分7分)已 ( http: / / www.21cnjy.com )知:如图,O为坐标原点,四边形OABC为矩形,A(10,0),C(0,4),点D是OA的中点,点P在BC上运动,当△ODP是腰长为5的等腰三角形时,求P点的坐标.
26.(2013.钦州)(本题满分6分)如图,在平面直角坐标系中,△ABC的三个顶点都在格点上,点A的坐标为(2,4),请解答下列问题:
(1)画出△ABC关于x轴对称的,并写出点的坐标.
(2)画出先向左平移3个单位长度,再向上平移4个单位长度得到的,并写出点的坐标.
27.(本题满分7分)在平面直角坐标系中,直线过点M(3,0),且平行于y轴.
(1)如果△ABC三个顶点的坐标分别是A(-2,0),B(-1,0),C(-1,2),△ABC关于y轴的对称图形是,关于直线l的对称图形是,写出的三个顶点的坐标;
(2)如果点P的坐标是,其中,点P关于y轴的对称点是,点关于直线的对称点是,求的长.
28.(本题满分8分)如图,长方形OA ( http: / / www.21cnjy.com )BC中,O为平面直角坐标系的原点,A点的坐标为(4,0),C点的坐标为(0,6),点B在第一象限内,点P从原点出发,以每秒2个单位长度的速度沿着O-A-B-C-O的路线移动(即:沿着长方形移动一周).
(1)写出点B的坐标( ).
(2)当点P移动了4秒时,描出此时P点的位置,并求出点P的坐标.
(3)在移动过程中,当点P到x轴距离为5个单位长度时,求点P移动的时间.
29.(本题满分8分)
(1)在平面直角坐标系中,将点A(-3,4)向右平移5个单位到点,再将点绕坐标原点顺时针旋转90°到点.直接写出点,的坐标;
(2)在平面直角坐标系中,将第二象限内的点B向右平移个单位到第一象限点,再将点绕坐标原点顺时针旋转90°到点,直接写出点,的坐标;
(3)在平面直角坐标系中.将点P(c,d)沿水平方向平移n个单位到点,再将点绕坐标原点顺时针旋转90°到点,直接写出点的坐标.
2014-2015学年第一学期初二数学第五单元测试题参考答案
一、选择题:
1.D;2.A;3.A;4.C;5.B;6.B;7.A;8.A;9.A;10.D;11.A;
二、填空题:
12.2,2;13.(-1,1);14.(-3,1);15.;16.4;17.2;18.;19.(2,-4);
三、解答题:
20. 解:(1)点A的坐标是(-2,0),点C的坐标是(1,2).
(2)连接AC,在Rt△ACD中,AD=OA+OD=3,CD=2,
∴=13,∴AC=.
21. 解:(1)平移后的△A′B′C′如图所示;
点A′、B′、C′的坐标分别为(-1,5)、(-4,0)、
(-1,0);
(2)由平移的性质可知,四边形AA′B′B是平行四边形,
∴△ABC扫过的面积=S四边形AA'B'B+ =B′B AC+BC AC=5×5+×3×5=25+=.
22. 解:(1)方法较多,如:先向右平移5小格,使点C移到点C′,再以C′为中心,顺时针方向旋转90°得到△A′B′C′;
(2)D(0,-2),E(-4,-4),F(2,-3).
作FG⊥b于M,交ED于G(如下图),则
=FG×DM+FG×1=4.
23. 解:(1)如图所示:
(2)如图所示:
(3)结合图形可得:B′(2,1);
(4)=3×4-×2×3-×1×2-×2×4=12-3-1-4=4.
24. 解:依题意可知,折痕AD是四边形OAED的对称轴,
∴在Rt△ABE中,AE=AO=10,AB=8,BE=6,
∴CE=4,∴E(4,8).在Rt△DCE中,,
又∵DE=OD,∴,∴OD=5,∴D(0,5),
综上D点坐标为(0,5)、E点坐标为(4,8).
25. 解:(1)OD是等腰三角形的底边时,P就是OD的垂直平分线与CB的交点,此时OP=PD≠5;
(2)OD是等腰三角形的一条腰时:
①若点O是顶角顶点时,P点就是以点O为圆心,以5为半径的弧与CB的交点,
在直角△OPC中,CP=3,则P的坐标是(3,4).
②若D是顶角顶点时,P点就是以点D为圆心,以5为半径的弧与CB的交点,
过D作DM⊥BC于点M,
在直角△PDM中,PM=,
当P在M的左边时,CP=5-3=2,则P的坐标是(2,4);
当P在M的右侧时,CP=5+3=8,则P的坐标是(8,4).
故P的坐标为:(3,4)或(2,4)或(8,4).
故答案为:(3,4)或(2,4)或(8,4).
26. 图略,点的坐标(2,-4);图略;点的坐标(-1,0);
27. 解:(1)的三个顶点的坐标分别是(4,0),(5,0),(5,2);
(2)如图1,当0<a≤3时,∵P与关于y轴对称,P(-a,0),
∴(a,0),又∵与关于l:直线x=3对称,
设(x,0),可得:,即,
∴(6-a,0),则PP2=6-a-(-a)=6-a+a=6.
如图2,当a>3时,
∵P与关于y轴对称,P(-a,0),
∴(a,0),
又∵与关于l:直线x=3对称,
设(x,0),可得:,即,
∴(6-a,0),
则=6-a-(-a)=6-a+a=6.
28. 解:(1)根据长方形的性质,可得AB与y轴平行,BC与x轴平行;故B的坐标为(4,6);
(2)根据题意,P的运动速度为每秒2个单位长度,当点P移动了4秒时,则其运动了8个长度单位,此时P的坐标为(4,4),位于AB上;
(3)根据题意,点P到x轴距离为5个单位长度时,有两种情况:
P在AB上时,P运动了4+5=9个长度单位,此时P运动了4.5秒;
P在OC上时,P运动了4+6+4+1=15个长度单位,此时P运动了=7.5秒.
29. 解:(1)如图,∵将点A(-3,4)向右平移5个单位到点,
∴的坐标为(2,4),
∵又将点绕坐标原点顺时针旋转90°到点,
∴,
∴的坐标(4,-2).
(2)根据(1)中的规律得:
的坐标为(a+m,b),的坐标为(b,-a-m).
(3)分两种情况:
①当把点P(c,d)沿水平方向右平移n个单位到点,
∴的坐标为(c+n,d),则的坐标为(d,-c-n);
②当把点P(c,d)沿水平方向左平移n个单位到点,
∴的坐标为(c-n,d),然后将点绕坐标原点顺时针旋转90°到点,
∴的坐标(d,-c+n).
A. B. C. D.
第14题图
第11题图
第19题图
第17题图
第18题图
命题:汤志良;审核:杨志刚;分值:130分;知识涵盖:平面直角坐标系.
卷首语:亲爱的同学:在最近这段时间,我们曾付出了辛勤的汗水,今天就让我们尽情采摘成功的果实吧!
一、选择题:(本题共11小题,每小题3分,共33分)
1.(2013.湛江)在平面直角坐标系中,点A(2,-3)在第……………………………( )象限.
A.一; B.二; C.三; D.四;
2.(2013 台湾)坐标平面上有一点A,且A点到轴的距离为3,A点到轴的距离恰为到轴距离的3倍.若A点在第二象限,则A点坐标为何?…………………………( )
A.(-9,3); B.(-3,1); C.(-3,9); D.(-1,3);
3.(2012 深圳)已知点P关于轴的对称点在第一象限,则的取值范围是……………………………………………………………………………………………( )
A.; B.;C.; D.;
4.(2013.遂宁)将点A(3,2)沿轴向左平移4个单位长度得到点A′,点A′关于轴对称的点的坐标是…………………………………………………………………………( )
A.(-3,2); B.(-1,2); C.(1,2); D.(1,-2);
5.(2013 曲靖)在平面直角坐标系中 ( http: / / www.21cnjy.com ),将点P(-2,1)向右平移3个单位长度,再向上平移4个单位长度得到点P′的坐标是………………………………………………………( )
A.(2,4); B.(1,5); C.(1,-3); D.(-5,5);
6.(2014 南安市二模)若点A在轴上,则点B在…………………( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
7.(2014 连云港)在平面直角坐标系内,点P(-2,3)关于原点的对称点Q的坐标为………………( )
A.(2,-3); B.(2,3); C.(3,-2); D.(-2,-3);
8.(2012.荆门)已知点M关于x轴的对称点在第一象限,则的取值范围在数轴上表示正确的是……………………………………………………………( )
9.点N在轴下方、轴左侧,且,,则点N的坐标为…( )
A.(-3,-2);B. (-3,2);C.(3,-2);D.(3,2);
10.(2013 东营)若定义:,,例如,=(-4,5),则=………………………………………( )
A.(2,-3); B.(-2,3); C.(2,3); D.(-2,-3);
11.将正整数按如图所示的规律排列下去,若 ( http: / / www.21cnjy.com )有序实数对(n,m)表示第n排从左到右第m个数,如(4,2)表示9,则表示58的有序数对是……………………( )
A.(11,3); B.(3,11); C.(11,9); D.(9,11);
二、填空题:(本题共8小题,每小题3分,共24分)
12. 在平面直角坐标系中,已知点A与点B关于原点对称,则= ,= .
13.(2013.天水)已知点M(3,-2 ( http: / / www.21cnjy.com )),将它先向左平移4个单位,再向上平移3个单位后得到点N,则点N的坐标是 .
14.如图,若在象棋盘上建立直角坐标系,使“帅”位于点(-1,-2).“馬”位于点(2,-2),则“兵”位于点 .
15.(2012.扬州)在平面直角坐标系中,点P在第一象限内,则的取值范围是 .
16.已知点P,则当= 时,点P在第一、三象限的角平分线上.
17.(2012.娄底)如图,A、B的坐标分别为(1,0)、(0,2),若将线段AB平移到至,、的坐标分别为、,则= .
18.(2013 东营)将 ( http: / / www.21cnjy.com )等腰直角三角形AOB按如图所示放置,然后绕点O逆时针旋转90°至△A′OB′的位置,点B的横坐标为2,则点A′的坐标为 .
19.(2013.抚顺)如图,在平面直角坐标系中,点A、B、C的坐标分别是(-1,-1)、(0,2)、(2,0),点P在y轴上,且坐标为(0,-2).点P关于点A的对称点为,点关于点B的对称点为,点关于点C的对称点为,点关于点A的对称点为,点关于点B的对称点为,点关于点C的对称点为,点关于点A的对称点为…,按此规律进行下去,则点的坐标是 .
三、解答题:(本题共10题,总分共73分)
20.(本题满分6分)如图,在直角坐标 ( http: / / www.21cnjy.com )系中,Rt△AOB的两条直角边OA,OB分别在x轴的负半轴,y轴的负半轴上,且OA=2,OB=1.将Rt△AOB绕点O按顺时针方向旋转90°,再把所得的像沿x轴正方向平移1个单位,得△CDO.
(1)写出点A,C的坐标;
(2)求点A和点C之间的距离.
21.(本题满分8分)(2013. ( http: / / www.21cnjy.com )晋江)如图,在方格纸中(小正方形的边长为1),△ABC的三个顶点均为格点,将△ABC沿x轴向左平移5个单位长度,根据所给的直角坐标系(O是坐标原点),解答下列问题:
(1)画出平移后的△A′B′C′,并直接写出点A′、B′、C′的坐标;
(2)求出在整个平移过程中,△ABC扫过的面积.
22.(本题满分8分)在如图所示的 ( http: / / www.21cnjy.com )方格图中,我们称每个小正方形的顶点为“格点”,以格点为顶点的三角形叫做“格点三角形”根据图形,解决下面的问题:
(1)图中的格点△A′B′C′是由格点△ABC通过哪些变换方法得到的?
(2)如果以直线,为坐标轴建立平面直角坐标系后,点A的坐标为(-3,4),请写出格点△DEF各顶点坐标,并求出△DEF的面积.
23.(本题满分8分)在如图所示的正方形网格 ( http: / / www.21cnjy.com )中,每个小正方形的边长为1,格点三角形(顶点是网格线的交点的三角形)ABC的顶点A、C的坐标分别为(-4,5),(-1,3).
(1)请在如图所示的网格平面内作出平面直角坐标系;
(2)请作出△ABC关于y轴对称的△A′B′C′;
(3)点B′的坐标为 .
(4)△ABC的面积为 .
24.(本题满分7分)如图 ( http: / / www.21cnjy.com ),OABC是一张放在平面直角坐标系中的长方形纸片,O为原点,点A在x轴的正半轴上,点C在y轴的正半轴上,OA=10,OC=8,在OC边上取一点D,将纸片沿AD翻折,使点O落在BC边上的点E处,求D、E两点的坐标.
25.(本题满分7分)已 ( http: / / www.21cnjy.com )知:如图,O为坐标原点,四边形OABC为矩形,A(10,0),C(0,4),点D是OA的中点,点P在BC上运动,当△ODP是腰长为5的等腰三角形时,求P点的坐标.
26.(2013.钦州)(本题满分6分)如图,在平面直角坐标系中,△ABC的三个顶点都在格点上,点A的坐标为(2,4),请解答下列问题:
(1)画出△ABC关于x轴对称的,并写出点的坐标.
(2)画出先向左平移3个单位长度,再向上平移4个单位长度得到的,并写出点的坐标.
27.(本题满分7分)在平面直角坐标系中,直线过点M(3,0),且平行于y轴.
(1)如果△ABC三个顶点的坐标分别是A(-2,0),B(-1,0),C(-1,2),△ABC关于y轴的对称图形是,关于直线l的对称图形是,写出的三个顶点的坐标;
(2)如果点P的坐标是,其中,点P关于y轴的对称点是,点关于直线的对称点是,求的长.
28.(本题满分8分)如图,长方形OA ( http: / / www.21cnjy.com )BC中,O为平面直角坐标系的原点,A点的坐标为(4,0),C点的坐标为(0,6),点B在第一象限内,点P从原点出发,以每秒2个单位长度的速度沿着O-A-B-C-O的路线移动(即:沿着长方形移动一周).
(1)写出点B的坐标( ).
(2)当点P移动了4秒时,描出此时P点的位置,并求出点P的坐标.
(3)在移动过程中,当点P到x轴距离为5个单位长度时,求点P移动的时间.
29.(本题满分8分)
(1)在平面直角坐标系中,将点A(-3,4)向右平移5个单位到点,再将点绕坐标原点顺时针旋转90°到点.直接写出点,的坐标;
(2)在平面直角坐标系中,将第二象限内的点B向右平移个单位到第一象限点,再将点绕坐标原点顺时针旋转90°到点,直接写出点,的坐标;
(3)在平面直角坐标系中.将点P(c,d)沿水平方向平移n个单位到点,再将点绕坐标原点顺时针旋转90°到点,直接写出点的坐标.
2014-2015学年第一学期初二数学第五单元测试题参考答案
一、选择题:
1.D;2.A;3.A;4.C;5.B;6.B;7.A;8.A;9.A;10.D;11.A;
二、填空题:
12.2,2;13.(-1,1);14.(-3,1);15.;16.4;17.2;18.;19.(2,-4);
三、解答题:
20. 解:(1)点A的坐标是(-2,0),点C的坐标是(1,2).
(2)连接AC,在Rt△ACD中,AD=OA+OD=3,CD=2,
∴=13,∴AC=.
21. 解:(1)平移后的△A′B′C′如图所示;
点A′、B′、C′的坐标分别为(-1,5)、(-4,0)、
(-1,0);
(2)由平移的性质可知,四边形AA′B′B是平行四边形,
∴△ABC扫过的面积=S四边形AA'B'B+ =B′B AC+BC AC=5×5+×3×5=25+=.
22. 解:(1)方法较多,如:先向右平移5小格,使点C移到点C′,再以C′为中心,顺时针方向旋转90°得到△A′B′C′;
(2)D(0,-2),E(-4,-4),F(2,-3).
作FG⊥b于M,交ED于G(如下图),则
=FG×DM+FG×1=4.
23. 解:(1)如图所示:
(2)如图所示:
(3)结合图形可得:B′(2,1);
(4)=3×4-×2×3-×1×2-×2×4=12-3-1-4=4.
24. 解:依题意可知,折痕AD是四边形OAED的对称轴,
∴在Rt△ABE中,AE=AO=10,AB=8,BE=6,
∴CE=4,∴E(4,8).在Rt△DCE中,,
又∵DE=OD,∴,∴OD=5,∴D(0,5),
综上D点坐标为(0,5)、E点坐标为(4,8).
25. 解:(1)OD是等腰三角形的底边时,P就是OD的垂直平分线与CB的交点,此时OP=PD≠5;
(2)OD是等腰三角形的一条腰时:
①若点O是顶角顶点时,P点就是以点O为圆心,以5为半径的弧与CB的交点,
在直角△OPC中,CP=3,则P的坐标是(3,4).
②若D是顶角顶点时,P点就是以点D为圆心,以5为半径的弧与CB的交点,
过D作DM⊥BC于点M,
在直角△PDM中,PM=,
当P在M的左边时,CP=5-3=2,则P的坐标是(2,4);
当P在M的右侧时,CP=5+3=8,则P的坐标是(8,4).
故P的坐标为:(3,4)或(2,4)或(8,4).
故答案为:(3,4)或(2,4)或(8,4).
26. 图略,点的坐标(2,-4);图略;点的坐标(-1,0);
27. 解:(1)的三个顶点的坐标分别是(4,0),(5,0),(5,2);
(2)如图1,当0<a≤3时,∵P与关于y轴对称,P(-a,0),
∴(a,0),又∵与关于l:直线x=3对称,
设(x,0),可得:,即,
∴(6-a,0),则PP2=6-a-(-a)=6-a+a=6.
如图2,当a>3时,
∵P与关于y轴对称,P(-a,0),
∴(a,0),
又∵与关于l:直线x=3对称,
设(x,0),可得:,即,
∴(6-a,0),
则=6-a-(-a)=6-a+a=6.
28. 解:(1)根据长方形的性质,可得AB与y轴平行,BC与x轴平行;故B的坐标为(4,6);
(2)根据题意,P的运动速度为每秒2个单位长度,当点P移动了4秒时,则其运动了8个长度单位,此时P的坐标为(4,4),位于AB上;
(3)根据题意,点P到x轴距离为5个单位长度时,有两种情况:
P在AB上时,P运动了4+5=9个长度单位,此时P运动了4.5秒;
P在OC上时,P运动了4+6+4+1=15个长度单位,此时P运动了=7.5秒.
29. 解:(1)如图,∵将点A(-3,4)向右平移5个单位到点,
∴的坐标为(2,4),
∵又将点绕坐标原点顺时针旋转90°到点,
∴,
∴的坐标(4,-2).
(2)根据(1)中的规律得:
的坐标为(a+m,b),的坐标为(b,-a-m).
(3)分两种情况:
①当把点P(c,d)沿水平方向右平移n个单位到点,
∴的坐标为(c+n,d),则的坐标为(d,-c-n);
②当把点P(c,d)沿水平方向左平移n个单位到点,
∴的坐标为(c-n,d),然后将点绕坐标原点顺时针旋转90°到点,
∴的坐标(d,-c+n).
A. B. C. D.
第14题图
第11题图
第19题图
第17题图
第18题图
同课章节目录
- 第一章 全等三角形
- 1.1 全等图形
- 1.2 全等三角形
- 1.3 探索三角形全等的条件
- 数学活动 关于三角形全等的条件
- 第二章 轴对称图形
- 2.1 轴对称与轴对称图形
- 2.2 轴对称的性质
- 2.3 设计轴对称图案
- 2.4 线段、角的轴对称性
- 2.5 等腰三角形的轴对称性
- 数学活动 折纸与证明
- 第三章 勾股定理
- 3.1 勾股定理
- 3.2 勾股定理的逆定理
- 3.3 勾股定理的简单应用
- 数学活动 探寻“勾股数”
- 第四章 实数
- 4.1 平方根
- 4.2 立方根
- 4.3 实数
- 4.4 近似数
- 数学活动 有关“实数”的课题探究
- 第五章 平面直角坐标系
- 5.1 物体位置的确定
- 5.2 平面直角坐标系
- 数学活动 确定藏宝地
- 第六章 一次函数
- 6.1 函数
- 6.2 一次函数
- 6.3 一次函数的图像
- 6.4 用一次函数解决问题
- 6.5 一次函数与二元一次方程
- 6.6 一次函数、一元一次方程和一元一次不等式
- 数学活动 温度计上的一次函数
