期中备考精选好题应用题专项(含答案)数学五年级下册苏教版
文档属性
| 名称 | 期中备考精选好题应用题专项(含答案)数学五年级下册苏教版 |  | |
| 格式 | docx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-04-18 14:57:35 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
期中备考精选好题(应用题专项)-数学五年级下册苏教版
1.A、B两个港口间的航程是210千米,甲、乙两船同时从A、B两个港口出发,相向而行,3小时后相遇。甲船每小时航行38千米,乙船每小时航行多少千米?
等量关系:( )行驶的路程+( )行驶的路程=总路程
速度和×( )=总路程
选择一个等量关系列方程解答:
2.有甲、乙两袋球,甲袋里有100个,乙袋里有72个。小刚每次从甲袋中取出3个球,同时往乙袋中放入4个球,像这样取放多少次后,甲、乙两袋球的数量相等?(先在表中填一填,再列式解答)
原来 取放1次后 取放2次后
甲袋/个
乙袋/个
相差/个
3.甲、乙两个工程队合挖一条长3200米的水渠,两队同一天开始。甲队每天挖45米,要保证在40天内完工,乙队每天至少挖多少米?
4.刘丽有32只千纸鹤,给妹妹3只后,她俩的千纸鹤就同样多了。妹妹原来有多少只千纸鹤?
5.办公室有一包白色打印纸,计划每天用30张,可以用28天。这包白色打印纸一共有多少张?由于注意了节约用纸,实际每天只用了20张,实际可以用多少天?
6.世界上最大的蜂鸟是巨蜂鸟,体长是230毫米,比世界上体型最小的鸟类古巴的吸蜜蜂鸟体长的4倍还多30毫米。古巴的吸蜜蜂鸟的体长约是多少毫米?
7.下面是两户人家的水费情况:
户主名 上次读数/吨 本次读数/吨 水费/元
李玉芳 3823 3848 70
陈云 4102 ? 126
陈云家本次的水表读数是多少?(水价:2.8元/吨)
水表上的读数表示水表安装以后的用水总量,两次读数的差就是这段时间里的用水吨数。
8.在一次跳绳比赛中,欣欣、丽丽和明明的1分钟跳绳数正好是三个连续的自然数。他们一共跳了351下,其中欣欣的成绩最差,明明的成绩最好。他们分别跳了多少下?
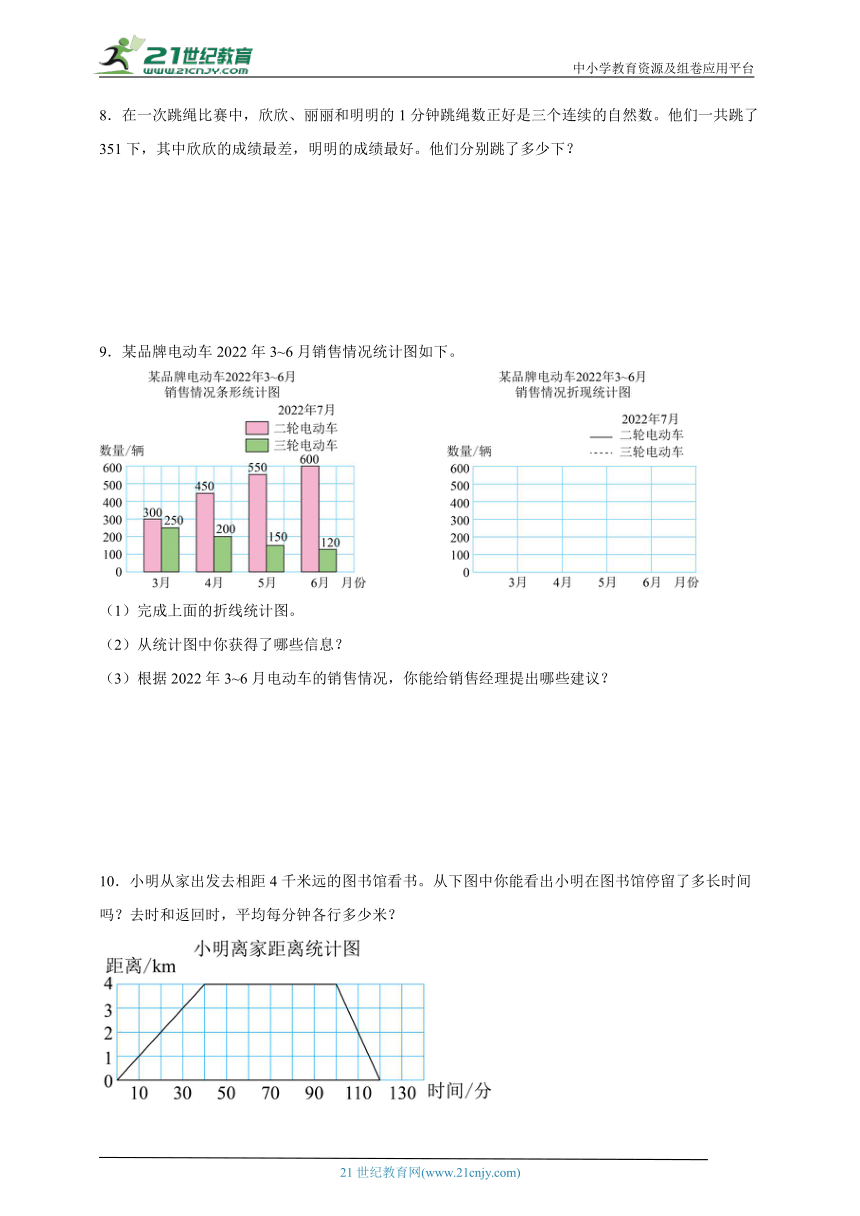
9.某品牌电动车2022年3~6月销售情况统计图如下。
(1)完成上面的折线统计图。
(2)从统计图中你获得了哪些信息?
(3)根据2022年3~6月电动车的销售情况,你能给销售经理提出哪些建议?
10.小明从家出发去相距4千米远的图书馆看书。从下图中你能看出小明在图书馆停留了多长时间吗?去时和返回时,平均每分钟各行多少米?
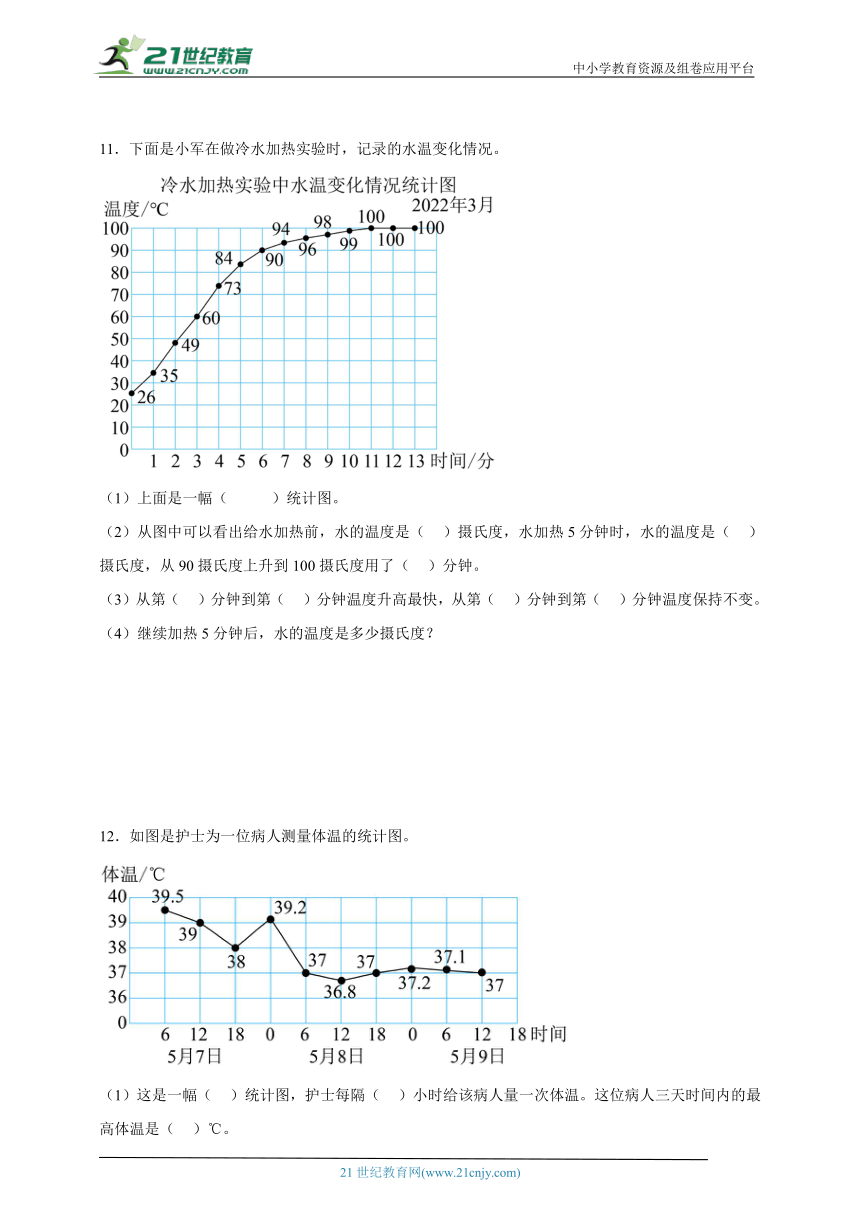
11.下面是小军在做冷水加热实验时,记录的水温变化情况。
(1)上面是一幅( )统计图。
(2)从图中可以看出给水加热前,水的温度是( )摄氏度,水加热5分钟时,水的温度是( )摄氏度,从90摄氏度上升到100摄氏度用了( )分钟。
(3)从第( )分钟到第( )分钟温度升高最快,从第( )分钟到第( )分钟温度保持不变。
(4)继续加热5分钟后,水的温度是多少摄氏度?
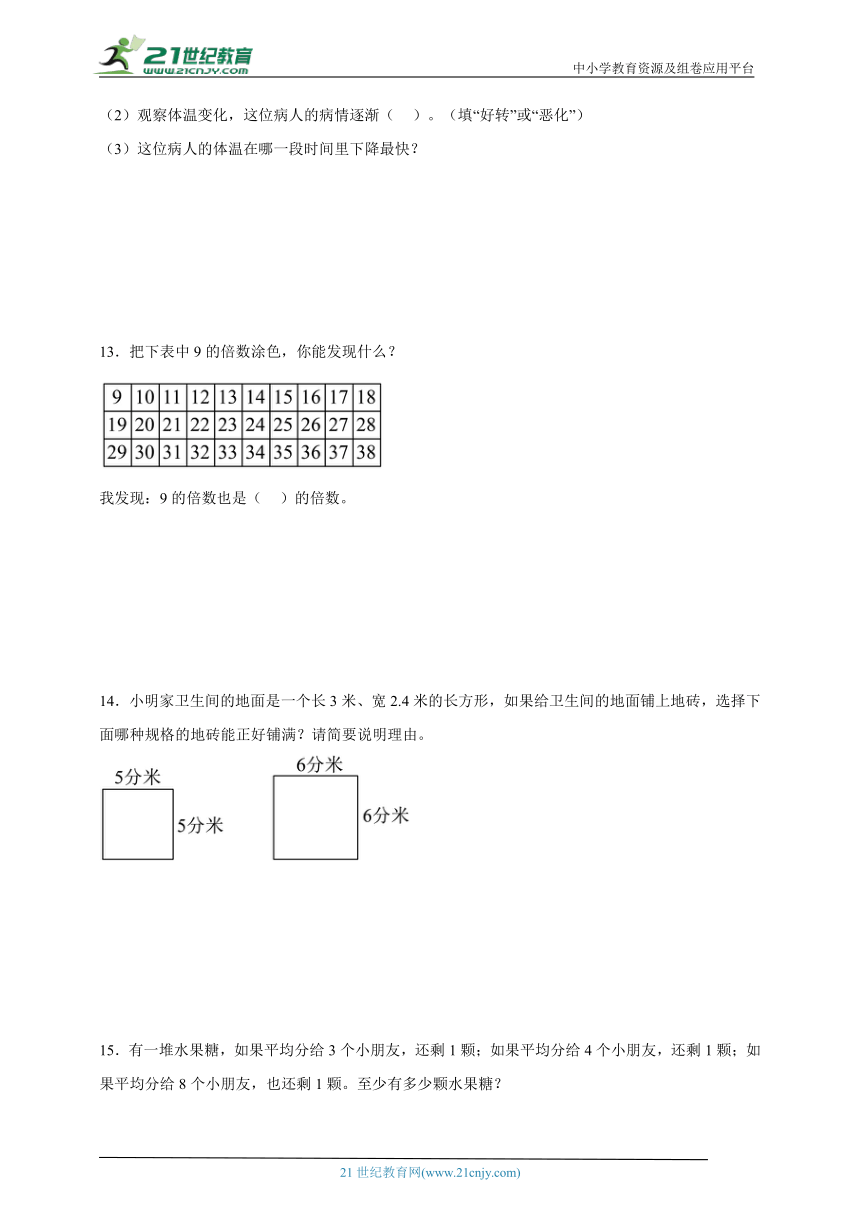
12.如图是护士为一位病人测量体温的统计图。
(1)这是一幅( )统计图,护士每隔( )小时给该病人量一次体温。这位病人三天时间内的最高体温是( )℃。
(2)观察体温变化,这位病人的病情逐渐( )。(填“好转”或“恶化”)
(3)这位病人的体温在哪一段时间里下降最快?
13.把下表中9的倍数涂色,你能发现什么?
我发现:9的倍数也是( )的倍数。
14.小明家卫生间的地面是一个长3米、宽2.4米的长方形,如果给卫生间的地面铺上地砖,选择下面哪种规格的地砖能正好铺满?请简要说明理由。
15.有一堆水果糖,如果平均分给3个小朋友,还剩1颗;如果平均分给4个小朋友,还剩1颗;如果平均分给8个小朋友,也还剩1颗。至少有多少颗水果糖?
16.妈妈买来一箱鸡蛋,有90多个,如果把它们装进8个一盒的蛋托中,正好装完;如果装进12个一盒的蛋托中,也正好装完。你能求出妈妈一共买了多少个鸡蛋吗?
17.三个小朋友,他们的年龄正好是三个连续的自然数,且他们年龄的积是60,这三个小朋友年龄最大的是多少岁?
18.如果四位数3A7B是3的倍数,那么A+B的和可以是多少?
19.乐乐观察2022年10月的月历,他想知道十一假期和周六周日共占这个月天数的几分之几,请你帮他算一算。
20.魔术师从魔盒里第一次拉出了1个正方体、2个球、3个圆柱;又拉了一次还是1个正方体、2个球、3个圆柱;第三次还是如此……就这样魔术师第8次拉出1个正方体、1个球时停止了,拉出的正方体的数量是球的几分之几?是圆柱的几分之几?
21.在下面三个框里涂色表示。
每个框中涂色的的数量一样多吗?为什么?
我的解答:_________________________________________________。
22.王叔叔准备去文具用品店采购一批铅笔,跑了三家店发现:甲店5元买8支;乙店3元买5支;丙店7元买8支送2支。请你帮王叔叔算一算,去哪家店购买最便宜?
23.从学校到科技馆,王强用了0.75小时,李峰用了40分钟,王洁用了小时,三人谁的速度最快?先把分数化成小数后再比较大小。
24.用3、5、7三个数字和分数线“—”,按要求组数。(每个分数中三个数字都用上且不重复)
(1)你能组成哪些真分数?
(2)你能组成哪些假分数?
参考答案:
1.见详解
【分析】根据相遇问题中,速度和×时间=路程和,设乙船每小时航行x千米,列方程为(38+x)×3=210,然后解出方程即可。
【详解】
如图:
等量关系:甲船行驶的路程+乙船行驶的路程=总路程
速度和×时间=总路程
解:设乙船每小时航行x千米。
(38+x)×3=210
(38+x)×3÷3=210÷3
38+x=70
38+x-38=70-38
x=32
答:乙船每小时航行32千米。
2.4次
【分析】
设像这样取放x次后,甲袋和乙袋数量正好相等,根据等量关系:甲袋原来的个数-取的次数×3=乙袋原来的个数+放的次数×4,列方程解答即可。
【详解】
原来 取放1次后 取放2次后 取放3次后 取放4次后
甲袋/个 100 97 94 91 88
乙袋/个 72 76 80 84 88
相差/个 28 21 14 7 0
解:像这样取放x次后,甲、乙两袋球的数量相等,
100-3x=72+4x
100-3x+3x=72+4x+3x
100=72+7x
72+7x-72=100-72
7x=28
7x÷7=28÷7
x=4
答:像这样取放4次后,甲、乙两袋球的数量相等。
3.35米
【分析】
根据题意可得出等量关系:甲队每天挖的长度×天数+乙队每天挖的长度×天数=水渠的全长,据此列出方程,并求解。
【详解】
解:设乙队每天至少挖米。
45×40+40=3200
1800+40=3200
1800+40-1800=3200-1800
40=1400
40÷40=1400÷40
=35
答:乙队每天至少挖35米。
4.26只
【分析】
根据题意,刘丽给妹妹3只后,她俩的千纸鹤就同样多了,可得出等量关系:妹妹原有千纸鹤的只数+3=刘丽原有千纸鹤的只数-3,据此列出方程,并求解。
【详解】
解:设妹妹原来有只千纸鹤。
+3=32-3
+3=29
+3-3=29-3
=26
答:妹妹原来有26只千纸鹤。
5.840张,42天
【分析】
根据题意,计划每天用30张,可以用28天,则白色打印纸的总张数为(30×28)页,设实际用了x天,实际每天用的张数×实际的天数=总张数,据此解答。
【详解】30×28=840(张)
解:设实际可以用x天,则:
20x=840
20x÷20=840÷20
x=42
答:实际可以用42天。
6.
50毫米
【分析】先找到巨蜂鸟与古巴的吸蜜蜂鸟的体长之间的关系,即巨蜂鸟体长=古巴的吸蜜蜂鸟体长的4倍+30毫米,则可设古巴的吸蜜蜂鸟体长为x毫米,根据找到的等量关系列方程,解方程即可。
【详解】解:设古巴的吸蜜蜂鸟的体长约是x毫米。
4x+30=230
4x+30-30=230-30
4x=200
x=50(毫米)
答:古巴的吸蜜蜂鸟的体长约是50毫米。
7.4147吨
【分析】
单价×数量=总价,设陈云家本次的水表读数是x吨,本次读数-上次读数=用水量,根据用水量×每吨价格=水费,列出方程解答即可。
【详解】
解:设陈云家本次的水表读数是x吨。
(x-4102)×2.8=126
(x-4102)×2.8÷2.8=126÷2.8
x-4102=45
x-4102+4102=45+4102
x=4147
答:陈云家本次的水表读数是4147吨。
8.欣欣116下;丽丽117下;明明118下
【分析】根据欣欣的成绩最差,明明的成绩最好,且三人的成绩是三个连续的自然数,可知丽丽比欣欣多跳1下,明明比丽丽多跳1下,则比欣欣多跳了2下;由此可以设欣欣跳了下,则丽丽跳了(+1)下,明明跳了(+2)下。
根据“他们一共跳了351下”可得出等量关系:欣欣跳的数量+丽丽跳的数量+明明跳的数量=三人跳的总数量,据此列出方程,并求解。
【详解】解:设欣欣跳了下,则丽丽跳了(+1)下,明明跳了(+2)下。
+(+1)+(+2)=351
3+3=351
3+3-3=351-3
3=348
3÷3=348÷3
=116
丽丽:116+1=117(下)
明明:116+2=118(下)
答:欣欣跳了116下,丽丽跳了117下,明明跳了118下。
9.(1)图见详解
(2)见详解
(3)见详解
【分析】
(1)本图为复式折线统计图,首先明确图例表示的意义,实线段表示的是二轮电动车数量,虚线段表示的是三轮电动车数量;根据各月销售量,在对应处描点,然后连接各点完成统计图;
(2)根据描出的复式折线统计图可知,二轮电动车销量逐月增加,三轮电动车销量逐月减少;
(3)根据市场需求,为销售经理提出合理建议即可,如应多进二轮电动车,少进三轮电动车。
【详解】
(1)如图:
(2)从统计图可知:二轮电动车的销售量逐渐增加,三轮电动车的销售量逐渐减少。
(3)根据2022年3~6月电动车的销售情况,我给销售经理提出的建议是:增加二轮电动车的进货量,减少三轮电动车的进货量。
10.60分钟;100米;200米
【分析】
从折线统计图中看出,小明从家出发走了40分钟到达了离家4千米的图书馆,在图书馆停留的时间是直线,没有发生距离的变化,这个直线的线段开始的点是第40分钟,结束的时间是第100分钟,再图书馆停留了60分钟。去时每分钟的路程=总路程÷去时的时间。返回每分钟的路程=总路程÷返回的时间。
【详解】在图书馆停留的时间:100-40=60(分钟)
4千米=4000米
去时:4000÷40=100(米)
返回时:4000÷(120-100)
=4000÷20
=200(米)
答:小明在图书馆停留了60分钟,去时平均每分钟行100米,返回时平均每分钟行200米。
11.(1)折线
(2)26;84;5
(3)1;2;11;13
(4)100摄氏度
【分析】
(1)用一个单位长度表示一定的数据,根据数量的多少描出各点,然后用线段顺次把各点连接起来,这样的统计图叫做折线统计图。
(2)从折线统计图中找到水加热前的温度,水加热5分钟时的温度;
从图中可知,6分钟时水温达到90摄氏度,11分钟时水温达到100摄氏度,用减法求出时间差即可。
(3)用减法求出相邻两个时间的温度差,再比较,找出温度上升最快的时间段。
观察折线统计图,折线水平时,表示此时水的温度保持不变。
(4)结合生活常识以及折线的变化趋势可知,水的最高温度是100摄氏度,达到这个温度后无论再加热多少分钟,都是100摄氏度。
【详解】(1)上面是一幅折线统计图。
(2)11-6=5(分钟)
从图中可以看出给水加热前,水的温度是26摄氏度,水加热5分钟时,水的温度是84摄氏度,从90摄氏度上升到100摄氏度用了5分钟。
(3)35-26=9(摄氏度)
49-35=14(摄氏度)
60-49=11(摄氏度)
73-60=13(摄氏度)
84-73=11(摄氏度)
90-84=6(摄氏度)
94-90=4(摄氏度)
96-94=2(摄氏度)
98-96=2(摄氏度)
99-98=1(摄氏度)
100-99=1(摄氏度)
100-100=0(摄氏度)
14>13>11>9>6>4>2>1>0
从第1分钟到第2分钟温度升高最快,从第11分钟到第13分钟温度保持不变。
(4)继续加热5分钟后,水的温度是100摄氏度。
12.(1)单式折线;6;39.5
(2)好转
(3)5月8日0时到6时
【分析】
(1)折线统计图用不同位置的点表示数量的多少,根据数量的多少描出各点,然后把各点用线段顺次连接起来。观察统计图,横轴表示测量体温的时间,求出相邻两个时间的差是间隔时间。数据点位置越高表示体温越高,据此填空。
(2)人体的正常体温一般在37℃左右,观察统计图,如果体温在正常体温左右表示病情好转,据此分析。
(3)折线往下表示下降趋势,折线往下坡度越陡表示体温下降越快,据此分析。
【详解】
(1)12-6=6(小时)
这是一幅单式折线统计图,护士每隔6小时给该病人量一次体温。这位病人三天时间内的最高体温是39.5℃。
(2)观察体温变化,这位病人的病情逐渐好转。
(3)这位病人的体温在5月8日0时到6时下降最快。
13.见详解;3
【分析】
先找出38以内9的倍数,并在表格中涂色;再判断9的倍数也是其它数的倍数,写出发现。
列乘法算式找倍数,按照从小到大的顺序,一组一组地写出这个数与非0自然数的乘法算式,乘法算式中的积就是这个数的倍数。
3的倍数特征:一个数各位上的数的和是3的倍数,这个数就是3的倍数。
【详解】38以内9的倍数有:9、18、27、36。
9、18、27、36都是3的倍数。
如下表:
我发现:9的倍数也是3的倍数。
14.6分米;理由见详解
【分析】根据题意,要将正方形地砖铺满长方形的区域,找到长和宽的公因数作为正方形的边长,则可正好铺满,据此解答。注意地砖的边长以分米为单位,可先将所有单位换算为分米,1米=10分米。
【详解】3米=30分米
2.4米=24分米
30的因数有:1、2、3、5、6、10、15、30;
24的因数有:1、2、3、4、6、8、12、24;
30和24的公因数有:1、2、3、6;
5不是30和24的公因数,6是30和24的公因数,所以选边长是6分米的正方形地砖能正好铺满;
答:选边长是6分米的正方形地砖能正好铺满,因为6是30和24的公因数。
15.25颗
【分析】根据题意,水果糖平均分给3个、4个、8个小朋友都还剩1颗,则水果糖的颗数比3、4、8的公倍数多1;问至少有多少颗水果糖,则水果糖的颗数为3、4、8的最小公倍数加1,据此解答。
【详解】
3、4、8的最小公倍数是:
(颗)
答:至少有25颗水果糖。
16.96个
【分析】根据题意,鸡蛋有90多个,且鸡蛋的个数既是8的倍数,也是12的倍数。求出8和12的最小公倍数,再用最小公倍数依次乘2、3、4、5……,直到得数为90多,据此解答。
【详解】
8和12的最小公倍数是:;
(个)
(个)
(个)
答:妈妈一共买了96个鸡蛋。
17.5岁
【分析】本题考查利用分解质因数解决问题,可先把60分解质因数,然后把结果写成三个连续自然数的积的形式,即可求得这三个小朋友中最大的年龄。
【详解】60=2×2×3×5
=3×4×5
因为3<4<5
因此年龄最大的是5岁。
答:这三个小朋友年龄最大的是5岁。
【点睛】
18.2、5、8、11、14、17
【分析】3的倍数特征:一个数各位上的数的和是3的倍数,这个数就是3的倍数。
根据题意,四位数3A7B是3的倍数,那么3+A+7+B=10+A+B是3的倍数,且最大的一位数是9,9+9=18,所以A+B的和不能大于18,据此得出A+B的和。
【详解】3+A+7+B=10+A+B
10+A+B是3的倍数,且A+B的和不能大于18,那么10+A+B<28;
10+A+B=12,则A+B=12-10=2;
10+A+B=15,则A+B=15-10=5;
10+A+B=18,则A+B=18-10=8;
10+A+B=21,则A+B=21-10=11;
10+A+B=24,则A+B=24-10=14;
10+A+B=27,则A+B=27-10=17。
答:A与B的和可以是2、5、8、11、14、17。
19.
【分析】
将这个月天数看作单位“1”,数出十一假期和周六周日的总天数,十一假期和周六周日的总天数÷这个月天数=十一假期和周六周日共占这个月天数的几分之几。
【详解】
答:十一假期和周六周日共占这个月天数的。
20.;
【分析】根据题意得:从魔盒中拉出了8次1个正方体、7次2个球加1个球、7次3个圆柱,可计算出拉出的正方体、球、圆柱的数量;用正方体数量÷球的数量,结果化为分数;用正方体数量÷圆柱数量,化为分数得出答案。
【详解】
正方体:8×1=8(个)
球:7×2+1=15(个)
圆柱:7×3=21(个)
正方体是球数量的:
正方体是圆柱数量的:
答:拉出的正方体的数量是球的,是圆柱的。
21.
见详解
【分析】由分数的意义知,表示把总量平均分成4份,取其中的3份,据此解答。
【详解】左框中涂色的数量 :
中框中涂色的数量:
右框中涂色的数量:
涂色如下:
我的解答:不一样多,因为不同的框中的总个数不一样多,所以它们的也不一样多。
22.乙店
【分析】
分数的分子相当于被除数,分母相当于除数,总价÷数量=单价,据此分别求出三个摊位铅笔的单价,比较即可。
【详解】甲店:(元)
乙店:(元)
丙店:7÷(8+2)
=7÷10
=0.7(元)
0.6<0.625<0.7
答:去乙店购买最便宜。
23.王洁
【分析】
先统一单位,根据1小时=60分钟,可知40分钟≈0.667小时,分数化成小数:用分子除以分母,按照除数是整数的小数除法进行计算;小数的大小比较必须先比较整数部分,若整数部分不同,整数部分按照整数比较大小的方法来比较,若整数部分相同,先比较小数部分的十分位,若十分位上的数字相同,再比较百分位,依此类推。
【详解】40分钟≈0.667小时
小时≈0.583小时
0.75小时>0.667小时>0.583小时
王洁花的时间最少。
答:王洁的速度最快。
24.(1)、、、、、
(2)、、、、、
【分析】
(1)真分数是分子比分母小的分数,所以组分数时,可以先确定分子。当分子是3时,真分数有、;当分子是5时,真分数有、;当分子是7时,真分数有、。
(2)假分数是分子比分母大或者分子和分母相等的分数,所以组分数时,可以先确定分母。当分母是3时,假分数有、;当分母是5时,假分数有、;当分母是7时,假分数有、。
【详解】
(1)真分数有:、、、、、
(2)假分数有:、、、、、
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
期中备考精选好题(应用题专项)-数学五年级下册苏教版
1.A、B两个港口间的航程是210千米,甲、乙两船同时从A、B两个港口出发,相向而行,3小时后相遇。甲船每小时航行38千米,乙船每小时航行多少千米?
等量关系:( )行驶的路程+( )行驶的路程=总路程
速度和×( )=总路程
选择一个等量关系列方程解答:
2.有甲、乙两袋球,甲袋里有100个,乙袋里有72个。小刚每次从甲袋中取出3个球,同时往乙袋中放入4个球,像这样取放多少次后,甲、乙两袋球的数量相等?(先在表中填一填,再列式解答)
原来 取放1次后 取放2次后
甲袋/个
乙袋/个
相差/个
3.甲、乙两个工程队合挖一条长3200米的水渠,两队同一天开始。甲队每天挖45米,要保证在40天内完工,乙队每天至少挖多少米?
4.刘丽有32只千纸鹤,给妹妹3只后,她俩的千纸鹤就同样多了。妹妹原来有多少只千纸鹤?
5.办公室有一包白色打印纸,计划每天用30张,可以用28天。这包白色打印纸一共有多少张?由于注意了节约用纸,实际每天只用了20张,实际可以用多少天?
6.世界上最大的蜂鸟是巨蜂鸟,体长是230毫米,比世界上体型最小的鸟类古巴的吸蜜蜂鸟体长的4倍还多30毫米。古巴的吸蜜蜂鸟的体长约是多少毫米?
7.下面是两户人家的水费情况:
户主名 上次读数/吨 本次读数/吨 水费/元
李玉芳 3823 3848 70
陈云 4102 ? 126
陈云家本次的水表读数是多少?(水价:2.8元/吨)
水表上的读数表示水表安装以后的用水总量,两次读数的差就是这段时间里的用水吨数。
8.在一次跳绳比赛中,欣欣、丽丽和明明的1分钟跳绳数正好是三个连续的自然数。他们一共跳了351下,其中欣欣的成绩最差,明明的成绩最好。他们分别跳了多少下?
9.某品牌电动车2022年3~6月销售情况统计图如下。
(1)完成上面的折线统计图。
(2)从统计图中你获得了哪些信息?
(3)根据2022年3~6月电动车的销售情况,你能给销售经理提出哪些建议?
10.小明从家出发去相距4千米远的图书馆看书。从下图中你能看出小明在图书馆停留了多长时间吗?去时和返回时,平均每分钟各行多少米?
11.下面是小军在做冷水加热实验时,记录的水温变化情况。
(1)上面是一幅( )统计图。
(2)从图中可以看出给水加热前,水的温度是( )摄氏度,水加热5分钟时,水的温度是( )摄氏度,从90摄氏度上升到100摄氏度用了( )分钟。
(3)从第( )分钟到第( )分钟温度升高最快,从第( )分钟到第( )分钟温度保持不变。
(4)继续加热5分钟后,水的温度是多少摄氏度?
12.如图是护士为一位病人测量体温的统计图。
(1)这是一幅( )统计图,护士每隔( )小时给该病人量一次体温。这位病人三天时间内的最高体温是( )℃。
(2)观察体温变化,这位病人的病情逐渐( )。(填“好转”或“恶化”)
(3)这位病人的体温在哪一段时间里下降最快?
13.把下表中9的倍数涂色,你能发现什么?
我发现:9的倍数也是( )的倍数。
14.小明家卫生间的地面是一个长3米、宽2.4米的长方形,如果给卫生间的地面铺上地砖,选择下面哪种规格的地砖能正好铺满?请简要说明理由。
15.有一堆水果糖,如果平均分给3个小朋友,还剩1颗;如果平均分给4个小朋友,还剩1颗;如果平均分给8个小朋友,也还剩1颗。至少有多少颗水果糖?
16.妈妈买来一箱鸡蛋,有90多个,如果把它们装进8个一盒的蛋托中,正好装完;如果装进12个一盒的蛋托中,也正好装完。你能求出妈妈一共买了多少个鸡蛋吗?
17.三个小朋友,他们的年龄正好是三个连续的自然数,且他们年龄的积是60,这三个小朋友年龄最大的是多少岁?
18.如果四位数3A7B是3的倍数,那么A+B的和可以是多少?
19.乐乐观察2022年10月的月历,他想知道十一假期和周六周日共占这个月天数的几分之几,请你帮他算一算。
20.魔术师从魔盒里第一次拉出了1个正方体、2个球、3个圆柱;又拉了一次还是1个正方体、2个球、3个圆柱;第三次还是如此……就这样魔术师第8次拉出1个正方体、1个球时停止了,拉出的正方体的数量是球的几分之几?是圆柱的几分之几?
21.在下面三个框里涂色表示。
每个框中涂色的的数量一样多吗?为什么?
我的解答:_________________________________________________。
22.王叔叔准备去文具用品店采购一批铅笔,跑了三家店发现:甲店5元买8支;乙店3元买5支;丙店7元买8支送2支。请你帮王叔叔算一算,去哪家店购买最便宜?
23.从学校到科技馆,王强用了0.75小时,李峰用了40分钟,王洁用了小时,三人谁的速度最快?先把分数化成小数后再比较大小。
24.用3、5、7三个数字和分数线“—”,按要求组数。(每个分数中三个数字都用上且不重复)
(1)你能组成哪些真分数?
(2)你能组成哪些假分数?
参考答案:
1.见详解
【分析】根据相遇问题中,速度和×时间=路程和,设乙船每小时航行x千米,列方程为(38+x)×3=210,然后解出方程即可。
【详解】
如图:
等量关系:甲船行驶的路程+乙船行驶的路程=总路程
速度和×时间=总路程
解:设乙船每小时航行x千米。
(38+x)×3=210
(38+x)×3÷3=210÷3
38+x=70
38+x-38=70-38
x=32
答:乙船每小时航行32千米。
2.4次
【分析】
设像这样取放x次后,甲袋和乙袋数量正好相等,根据等量关系:甲袋原来的个数-取的次数×3=乙袋原来的个数+放的次数×4,列方程解答即可。
【详解】
原来 取放1次后 取放2次后 取放3次后 取放4次后
甲袋/个 100 97 94 91 88
乙袋/个 72 76 80 84 88
相差/个 28 21 14 7 0
解:像这样取放x次后,甲、乙两袋球的数量相等,
100-3x=72+4x
100-3x+3x=72+4x+3x
100=72+7x
72+7x-72=100-72
7x=28
7x÷7=28÷7
x=4
答:像这样取放4次后,甲、乙两袋球的数量相等。
3.35米
【分析】
根据题意可得出等量关系:甲队每天挖的长度×天数+乙队每天挖的长度×天数=水渠的全长,据此列出方程,并求解。
【详解】
解:设乙队每天至少挖米。
45×40+40=3200
1800+40=3200
1800+40-1800=3200-1800
40=1400
40÷40=1400÷40
=35
答:乙队每天至少挖35米。
4.26只
【分析】
根据题意,刘丽给妹妹3只后,她俩的千纸鹤就同样多了,可得出等量关系:妹妹原有千纸鹤的只数+3=刘丽原有千纸鹤的只数-3,据此列出方程,并求解。
【详解】
解:设妹妹原来有只千纸鹤。
+3=32-3
+3=29
+3-3=29-3
=26
答:妹妹原来有26只千纸鹤。
5.840张,42天
【分析】
根据题意,计划每天用30张,可以用28天,则白色打印纸的总张数为(30×28)页,设实际用了x天,实际每天用的张数×实际的天数=总张数,据此解答。
【详解】30×28=840(张)
解:设实际可以用x天,则:
20x=840
20x÷20=840÷20
x=42
答:实际可以用42天。
6.
50毫米
【分析】先找到巨蜂鸟与古巴的吸蜜蜂鸟的体长之间的关系,即巨蜂鸟体长=古巴的吸蜜蜂鸟体长的4倍+30毫米,则可设古巴的吸蜜蜂鸟体长为x毫米,根据找到的等量关系列方程,解方程即可。
【详解】解:设古巴的吸蜜蜂鸟的体长约是x毫米。
4x+30=230
4x+30-30=230-30
4x=200
x=50(毫米)
答:古巴的吸蜜蜂鸟的体长约是50毫米。
7.4147吨
【分析】
单价×数量=总价,设陈云家本次的水表读数是x吨,本次读数-上次读数=用水量,根据用水量×每吨价格=水费,列出方程解答即可。
【详解】
解:设陈云家本次的水表读数是x吨。
(x-4102)×2.8=126
(x-4102)×2.8÷2.8=126÷2.8
x-4102=45
x-4102+4102=45+4102
x=4147
答:陈云家本次的水表读数是4147吨。
8.欣欣116下;丽丽117下;明明118下
【分析】根据欣欣的成绩最差,明明的成绩最好,且三人的成绩是三个连续的自然数,可知丽丽比欣欣多跳1下,明明比丽丽多跳1下,则比欣欣多跳了2下;由此可以设欣欣跳了下,则丽丽跳了(+1)下,明明跳了(+2)下。
根据“他们一共跳了351下”可得出等量关系:欣欣跳的数量+丽丽跳的数量+明明跳的数量=三人跳的总数量,据此列出方程,并求解。
【详解】解:设欣欣跳了下,则丽丽跳了(+1)下,明明跳了(+2)下。
+(+1)+(+2)=351
3+3=351
3+3-3=351-3
3=348
3÷3=348÷3
=116
丽丽:116+1=117(下)
明明:116+2=118(下)
答:欣欣跳了116下,丽丽跳了117下,明明跳了118下。
9.(1)图见详解
(2)见详解
(3)见详解
【分析】
(1)本图为复式折线统计图,首先明确图例表示的意义,实线段表示的是二轮电动车数量,虚线段表示的是三轮电动车数量;根据各月销售量,在对应处描点,然后连接各点完成统计图;
(2)根据描出的复式折线统计图可知,二轮电动车销量逐月增加,三轮电动车销量逐月减少;
(3)根据市场需求,为销售经理提出合理建议即可,如应多进二轮电动车,少进三轮电动车。
【详解】
(1)如图:
(2)从统计图可知:二轮电动车的销售量逐渐增加,三轮电动车的销售量逐渐减少。
(3)根据2022年3~6月电动车的销售情况,我给销售经理提出的建议是:增加二轮电动车的进货量,减少三轮电动车的进货量。
10.60分钟;100米;200米
【分析】
从折线统计图中看出,小明从家出发走了40分钟到达了离家4千米的图书馆,在图书馆停留的时间是直线,没有发生距离的变化,这个直线的线段开始的点是第40分钟,结束的时间是第100分钟,再图书馆停留了60分钟。去时每分钟的路程=总路程÷去时的时间。返回每分钟的路程=总路程÷返回的时间。
【详解】在图书馆停留的时间:100-40=60(分钟)
4千米=4000米
去时:4000÷40=100(米)
返回时:4000÷(120-100)
=4000÷20
=200(米)
答:小明在图书馆停留了60分钟,去时平均每分钟行100米,返回时平均每分钟行200米。
11.(1)折线
(2)26;84;5
(3)1;2;11;13
(4)100摄氏度
【分析】
(1)用一个单位长度表示一定的数据,根据数量的多少描出各点,然后用线段顺次把各点连接起来,这样的统计图叫做折线统计图。
(2)从折线统计图中找到水加热前的温度,水加热5分钟时的温度;
从图中可知,6分钟时水温达到90摄氏度,11分钟时水温达到100摄氏度,用减法求出时间差即可。
(3)用减法求出相邻两个时间的温度差,再比较,找出温度上升最快的时间段。
观察折线统计图,折线水平时,表示此时水的温度保持不变。
(4)结合生活常识以及折线的变化趋势可知,水的最高温度是100摄氏度,达到这个温度后无论再加热多少分钟,都是100摄氏度。
【详解】(1)上面是一幅折线统计图。
(2)11-6=5(分钟)
从图中可以看出给水加热前,水的温度是26摄氏度,水加热5分钟时,水的温度是84摄氏度,从90摄氏度上升到100摄氏度用了5分钟。
(3)35-26=9(摄氏度)
49-35=14(摄氏度)
60-49=11(摄氏度)
73-60=13(摄氏度)
84-73=11(摄氏度)
90-84=6(摄氏度)
94-90=4(摄氏度)
96-94=2(摄氏度)
98-96=2(摄氏度)
99-98=1(摄氏度)
100-99=1(摄氏度)
100-100=0(摄氏度)
14>13>11>9>6>4>2>1>0
从第1分钟到第2分钟温度升高最快,从第11分钟到第13分钟温度保持不变。
(4)继续加热5分钟后,水的温度是100摄氏度。
12.(1)单式折线;6;39.5
(2)好转
(3)5月8日0时到6时
【分析】
(1)折线统计图用不同位置的点表示数量的多少,根据数量的多少描出各点,然后把各点用线段顺次连接起来。观察统计图,横轴表示测量体温的时间,求出相邻两个时间的差是间隔时间。数据点位置越高表示体温越高,据此填空。
(2)人体的正常体温一般在37℃左右,观察统计图,如果体温在正常体温左右表示病情好转,据此分析。
(3)折线往下表示下降趋势,折线往下坡度越陡表示体温下降越快,据此分析。
【详解】
(1)12-6=6(小时)
这是一幅单式折线统计图,护士每隔6小时给该病人量一次体温。这位病人三天时间内的最高体温是39.5℃。
(2)观察体温变化,这位病人的病情逐渐好转。
(3)这位病人的体温在5月8日0时到6时下降最快。
13.见详解;3
【分析】
先找出38以内9的倍数,并在表格中涂色;再判断9的倍数也是其它数的倍数,写出发现。
列乘法算式找倍数,按照从小到大的顺序,一组一组地写出这个数与非0自然数的乘法算式,乘法算式中的积就是这个数的倍数。
3的倍数特征:一个数各位上的数的和是3的倍数,这个数就是3的倍数。
【详解】38以内9的倍数有:9、18、27、36。
9、18、27、36都是3的倍数。
如下表:
我发现:9的倍数也是3的倍数。
14.6分米;理由见详解
【分析】根据题意,要将正方形地砖铺满长方形的区域,找到长和宽的公因数作为正方形的边长,则可正好铺满,据此解答。注意地砖的边长以分米为单位,可先将所有单位换算为分米,1米=10分米。
【详解】3米=30分米
2.4米=24分米
30的因数有:1、2、3、5、6、10、15、30;
24的因数有:1、2、3、4、6、8、12、24;
30和24的公因数有:1、2、3、6;
5不是30和24的公因数,6是30和24的公因数,所以选边长是6分米的正方形地砖能正好铺满;
答:选边长是6分米的正方形地砖能正好铺满,因为6是30和24的公因数。
15.25颗
【分析】根据题意,水果糖平均分给3个、4个、8个小朋友都还剩1颗,则水果糖的颗数比3、4、8的公倍数多1;问至少有多少颗水果糖,则水果糖的颗数为3、4、8的最小公倍数加1,据此解答。
【详解】
3、4、8的最小公倍数是:
(颗)
答:至少有25颗水果糖。
16.96个
【分析】根据题意,鸡蛋有90多个,且鸡蛋的个数既是8的倍数,也是12的倍数。求出8和12的最小公倍数,再用最小公倍数依次乘2、3、4、5……,直到得数为90多,据此解答。
【详解】
8和12的最小公倍数是:;
(个)
(个)
(个)
答:妈妈一共买了96个鸡蛋。
17.5岁
【分析】本题考查利用分解质因数解决问题,可先把60分解质因数,然后把结果写成三个连续自然数的积的形式,即可求得这三个小朋友中最大的年龄。
【详解】60=2×2×3×5
=3×4×5
因为3<4<5
因此年龄最大的是5岁。
答:这三个小朋友年龄最大的是5岁。
【点睛】
18.2、5、8、11、14、17
【分析】3的倍数特征:一个数各位上的数的和是3的倍数,这个数就是3的倍数。
根据题意,四位数3A7B是3的倍数,那么3+A+7+B=10+A+B是3的倍数,且最大的一位数是9,9+9=18,所以A+B的和不能大于18,据此得出A+B的和。
【详解】3+A+7+B=10+A+B
10+A+B是3的倍数,且A+B的和不能大于18,那么10+A+B<28;
10+A+B=12,则A+B=12-10=2;
10+A+B=15,则A+B=15-10=5;
10+A+B=18,则A+B=18-10=8;
10+A+B=21,则A+B=21-10=11;
10+A+B=24,则A+B=24-10=14;
10+A+B=27,则A+B=27-10=17。
答:A与B的和可以是2、5、8、11、14、17。
19.
【分析】
将这个月天数看作单位“1”,数出十一假期和周六周日的总天数,十一假期和周六周日的总天数÷这个月天数=十一假期和周六周日共占这个月天数的几分之几。
【详解】
答:十一假期和周六周日共占这个月天数的。
20.;
【分析】根据题意得:从魔盒中拉出了8次1个正方体、7次2个球加1个球、7次3个圆柱,可计算出拉出的正方体、球、圆柱的数量;用正方体数量÷球的数量,结果化为分数;用正方体数量÷圆柱数量,化为分数得出答案。
【详解】
正方体:8×1=8(个)
球:7×2+1=15(个)
圆柱:7×3=21(个)
正方体是球数量的:
正方体是圆柱数量的:
答:拉出的正方体的数量是球的,是圆柱的。
21.
见详解
【分析】由分数的意义知,表示把总量平均分成4份,取其中的3份,据此解答。
【详解】左框中涂色的数量 :
中框中涂色的数量:
右框中涂色的数量:
涂色如下:
我的解答:不一样多,因为不同的框中的总个数不一样多,所以它们的也不一样多。
22.乙店
【分析】
分数的分子相当于被除数,分母相当于除数,总价÷数量=单价,据此分别求出三个摊位铅笔的单价,比较即可。
【详解】甲店:(元)
乙店:(元)
丙店:7÷(8+2)
=7÷10
=0.7(元)
0.6<0.625<0.7
答:去乙店购买最便宜。
23.王洁
【分析】
先统一单位,根据1小时=60分钟,可知40分钟≈0.667小时,分数化成小数:用分子除以分母,按照除数是整数的小数除法进行计算;小数的大小比较必须先比较整数部分,若整数部分不同,整数部分按照整数比较大小的方法来比较,若整数部分相同,先比较小数部分的十分位,若十分位上的数字相同,再比较百分位,依此类推。
【详解】40分钟≈0.667小时
小时≈0.583小时
0.75小时>0.667小时>0.583小时
王洁花的时间最少。
答:王洁的速度最快。
24.(1)、、、、、
(2)、、、、、
【分析】
(1)真分数是分子比分母小的分数,所以组分数时,可以先确定分子。当分子是3时,真分数有、;当分子是5时,真分数有、;当分子是7时,真分数有、。
(2)假分数是分子比分母大或者分子和分母相等的分数,所以组分数时,可以先确定分母。当分母是3时,假分数有、;当分母是5时,假分数有、;当分母是7时,假分数有、。
【详解】
(1)真分数有:、、、、、
(2)假分数有:、、、、、
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
