8.5.3 平面与平面平行 课件(共26张PPT)
文档属性
| 名称 | 8.5.3 平面与平面平行 课件(共26张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-04-17 10:37:09 | ||
图片预览






文档简介
(共26张PPT)
单/击/此/处/添/加/副/标/题/内/容
8.5.3 平面与平面平行
创设情境 引入新课
问题1 请同学们观察图片中房屋的屋顶的两个斜面之间、双层床的上下铺的床板面之间有怎样的位置关系?
创设情境 引入新课
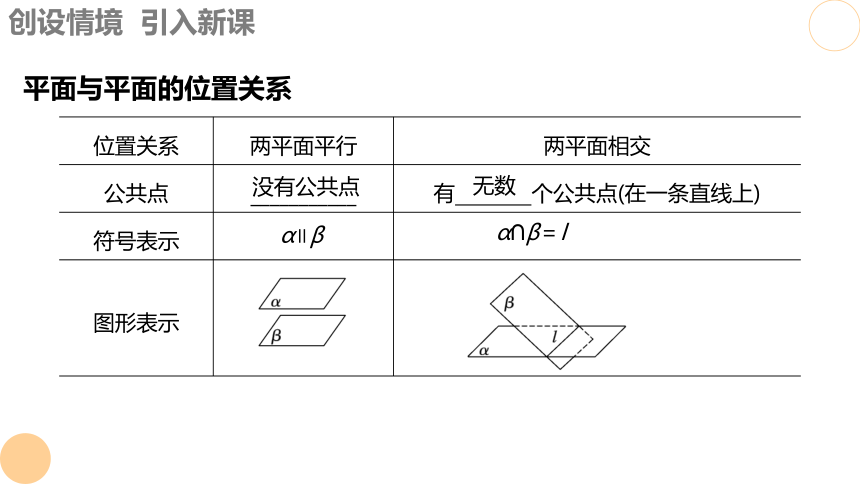
平面与平面的位置关系
位置关系 两平面平行 两平面相交
公共点 ___________ 有 个公共点(在一条直线上)
符号表示
图形表示
没有公共点
无数
α∥β
α∩β=l
问题2 除定义外,有没有更为简便的判定两个平面平行的方法呢?
启发引导 探求新知
合作探究 生成新知
学生动手做实验:用水平仪检验桌面是否水平?
根据实验结果请思考下面的问题并口答:
若平面β内一条直线与平面α平行,能否判断α∥β?
两条呢?无数条呢?
合作探究 生成新知
在实际生活中,工人师傅将水平仪在桌面上交叉放置两次,如果水平仪的气泡两次都在中央,就能判断桌面是水平的
合作探究 生成新知
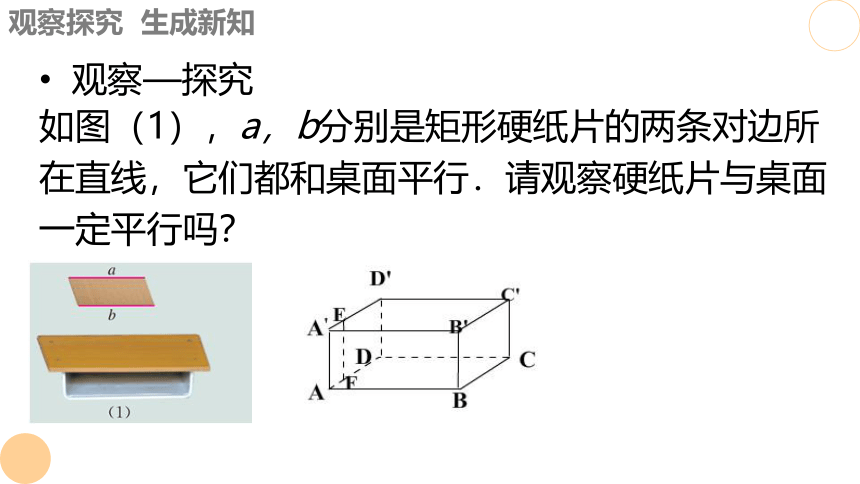
观察—探究
如图(1),a,b分别是矩形硬纸片的两条对边所在直线,它们都和桌面平行.请观察硬纸片与桌面一定平行吗?
观察探究 生成新知
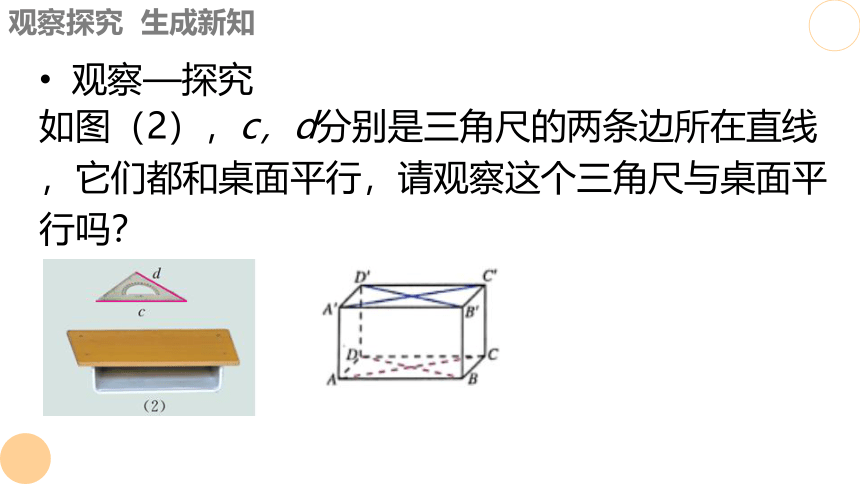
观察—探究
如图(2),c,d分别是三角尺的两条边所在直线,它们都和桌面平行,请观察这个三角尺与桌面平行吗?
观察探究 生成新知
你能从中总结出判定平面与平面平行的方法吗?
问题3
请分别用文字语言、图形语言、符号语言来表述.
启发引导 生成新知
总结提炼 生成新知
平面与平面平行的判定定理:
图形表示:
一个平面内的两条相交直线与另一个平面平行,则这两个
平面平行.
α
a
b
P
β
符号表示:
线面平行
面面平行
,a∥α,b∥α
β∥α.
为什么不能用“一个平面内的两条平行直线平行于另一个平面”判断两个平面平行,而可以用“一个平面内的两条相交直线平行于另一个平面”判断两个平面平行?联想平面向量基本定理,你能对面面平行判定定理做出进一步解释吗?
平面与平面平行的判定定理的深入理解:
概念辨析 领悟升华
平面内的两条相交直线代表两个不共线向量,而平面内的任意向量可以表示为它们的线性组合,从而平面内的两条相交直线可以“代表”这个平面上的任意一条直线;而两条平行直线所表示的向量是共线的,用它们不能“表示”这个平面上的任意一条直线.
概念辨析 领悟升华
典例示范 升华提高
例1 如图,已知正方体ABCD-A1B1C1D1.
求证:平面AB1D1//平面BC1D.
看到要证明的结论,你能想到用什么方法?
平面AB1D1和平面BC1D哪个平面中的两条相交直线平行另一个平面?又怎样证明一条直线平行于一个平面呢?
例1 如图,已知正方体ABCD-A1B1C1D1.
求证:平面AB1D1//平面BC1D.
证明:因为ABCD-A1B1C1D1为正方体,
∴ .
∴ .
∴ 四边形D1C1BA为平行四边形.∴D1A∥C1B.
又 D1A 平面BC1D,C1B 平面BC1D,∴D1A∥平面BC1D.
同理 D1B1∥平面BC1D.
又 D1A∩D1B1=D1,∴平面AB1D1//平面BC1D.
典例示范 升华提高
你能从中总结出证明平面与平面平行的一般步骤吗?
问题4
归纳小结 深化认知
面面平行
线面平行
线线平行
(1)如果两个平面平行,那么一个平面内的直线与另一个平面有什么位置关系?
合作探究 生成新知
问题5 如果两个平面平行,会有哪些结论呢?进行以下的三个探究活动:
(2)如果两个平面平行,两个平面内的直线有什么位置关系?
合作探究 生成新知
问题5 如果两个平面平行,会有哪些结论呢?进行以下的三个探究活动:
在如图所示的长方体中,请在平面AC内过点D作出平行于直线B′D′的直线.说明作法.
由直线B′D′和点D可以确定一个平面,这个平面也是平行直线DD′和BB′确定的平面,它与平面AC有唯一过点D的公共直线BD,直线BD与直线B′D′都在直线B′D′和点D确定平面内,且没有公共点,所以BD∥B′D′.
合作探究 生成新知
(3)在分别位于两个平行平面内的直线中,平行是一种特殊情况,什么时候这两条直线平行呢?
图形表示:
两个平面平行,如果一个平面与这两个平面相交,那么两条交线平行.
符号表示:
面面平行
线线平行
你能证明该性质定理吗?
平面与平面平行的性质定理
α∥β,α∩γ=a,β∩γ=b
a∥b.
总结提炼 生成新知
如图,α∥β,AB∥CD,且A∈α,C∈α,B∈β,D∈β.
求证:AB=CD.
在本题条件下,要证明AB=CD,你想到了什么?
构造平行四边形.
AB与CD是一个平行四边形的一组对边,那么另一组对边怎么
构造呢?题目的条件如何使用?
过平行线AB,CD作平面γ,与平面α和β分别相交于AC和BD.
典例示范 升华提高
β
A
C
B
D
例2 求证:夹在两个平行平面间的平行线段相等.
如图,α∥β,AB∥CD,且A∈α,C∈α,B∈β,D∈β.
求证:AB=CD.
证明:过平行线AB,CD作平面γ,与平面α和β分别相交于AC和BD.
∵α∥β, ∴BD∥AC.
又 AB∥CD, ∴四边形ABCD是平行四边形.
∴ AB=CD.
典例示范 升华提高
例2 求证:夹在两个平行平面间的平行线段相等.
归纳小结 深化认知
问题6 你能从中总结出证明直线与直线平行的一般步骤吗?
回顾反思 领悟提升
课堂小结
直观感知
操作确认
思辨论证
回顾反思 领悟提升
直线与直线平行
直线与平面平行
平面与平面平行
(判定)
(性质 )
(定义 )
( 性质 )
( 判定 )
课堂小结
a
b
α
a
b
α
β
α
a
b
P
β
空间平行关系如何相互转化:
课后训练 巩固拓展
作业练习+教科书习题8.5第8题
单/击/此/处/添/加/副/标/题/内/容
8.5.3 平面与平面平行
创设情境 引入新课
问题1 请同学们观察图片中房屋的屋顶的两个斜面之间、双层床的上下铺的床板面之间有怎样的位置关系?
创设情境 引入新课
平面与平面的位置关系
位置关系 两平面平行 两平面相交
公共点 ___________ 有 个公共点(在一条直线上)
符号表示
图形表示
没有公共点
无数
α∥β
α∩β=l
问题2 除定义外,有没有更为简便的判定两个平面平行的方法呢?
启发引导 探求新知
合作探究 生成新知
学生动手做实验:用水平仪检验桌面是否水平?
根据实验结果请思考下面的问题并口答:
若平面β内一条直线与平面α平行,能否判断α∥β?
两条呢?无数条呢?
合作探究 生成新知
在实际生活中,工人师傅将水平仪在桌面上交叉放置两次,如果水平仪的气泡两次都在中央,就能判断桌面是水平的
合作探究 生成新知
观察—探究
如图(1),a,b分别是矩形硬纸片的两条对边所在直线,它们都和桌面平行.请观察硬纸片与桌面一定平行吗?
观察探究 生成新知
观察—探究
如图(2),c,d分别是三角尺的两条边所在直线,它们都和桌面平行,请观察这个三角尺与桌面平行吗?
观察探究 生成新知
你能从中总结出判定平面与平面平行的方法吗?
问题3
请分别用文字语言、图形语言、符号语言来表述.
启发引导 生成新知
总结提炼 生成新知
平面与平面平行的判定定理:
图形表示:
一个平面内的两条相交直线与另一个平面平行,则这两个
平面平行.
α
a
b
P
β
符号表示:
线面平行
面面平行
,a∥α,b∥α
β∥α.
为什么不能用“一个平面内的两条平行直线平行于另一个平面”判断两个平面平行,而可以用“一个平面内的两条相交直线平行于另一个平面”判断两个平面平行?联想平面向量基本定理,你能对面面平行判定定理做出进一步解释吗?
平面与平面平行的判定定理的深入理解:
概念辨析 领悟升华
平面内的两条相交直线代表两个不共线向量,而平面内的任意向量可以表示为它们的线性组合,从而平面内的两条相交直线可以“代表”这个平面上的任意一条直线;而两条平行直线所表示的向量是共线的,用它们不能“表示”这个平面上的任意一条直线.
概念辨析 领悟升华
典例示范 升华提高
例1 如图,已知正方体ABCD-A1B1C1D1.
求证:平面AB1D1//平面BC1D.
看到要证明的结论,你能想到用什么方法?
平面AB1D1和平面BC1D哪个平面中的两条相交直线平行另一个平面?又怎样证明一条直线平行于一个平面呢?
例1 如图,已知正方体ABCD-A1B1C1D1.
求证:平面AB1D1//平面BC1D.
证明:因为ABCD-A1B1C1D1为正方体,
∴ .
∴ .
∴ 四边形D1C1BA为平行四边形.∴D1A∥C1B.
又 D1A 平面BC1D,C1B 平面BC1D,∴D1A∥平面BC1D.
同理 D1B1∥平面BC1D.
又 D1A∩D1B1=D1,∴平面AB1D1//平面BC1D.
典例示范 升华提高
你能从中总结出证明平面与平面平行的一般步骤吗?
问题4
归纳小结 深化认知
面面平行
线面平行
线线平行
(1)如果两个平面平行,那么一个平面内的直线与另一个平面有什么位置关系?
合作探究 生成新知
问题5 如果两个平面平行,会有哪些结论呢?进行以下的三个探究活动:
(2)如果两个平面平行,两个平面内的直线有什么位置关系?
合作探究 生成新知
问题5 如果两个平面平行,会有哪些结论呢?进行以下的三个探究活动:
在如图所示的长方体中,请在平面AC内过点D作出平行于直线B′D′的直线.说明作法.
由直线B′D′和点D可以确定一个平面,这个平面也是平行直线DD′和BB′确定的平面,它与平面AC有唯一过点D的公共直线BD,直线BD与直线B′D′都在直线B′D′和点D确定平面内,且没有公共点,所以BD∥B′D′.
合作探究 生成新知
(3)在分别位于两个平行平面内的直线中,平行是一种特殊情况,什么时候这两条直线平行呢?
图形表示:
两个平面平行,如果一个平面与这两个平面相交,那么两条交线平行.
符号表示:
面面平行
线线平行
你能证明该性质定理吗?
平面与平面平行的性质定理
α∥β,α∩γ=a,β∩γ=b
a∥b.
总结提炼 生成新知
如图,α∥β,AB∥CD,且A∈α,C∈α,B∈β,D∈β.
求证:AB=CD.
在本题条件下,要证明AB=CD,你想到了什么?
构造平行四边形.
AB与CD是一个平行四边形的一组对边,那么另一组对边怎么
构造呢?题目的条件如何使用?
过平行线AB,CD作平面γ,与平面α和β分别相交于AC和BD.
典例示范 升华提高
β
A
C
B
D
例2 求证:夹在两个平行平面间的平行线段相等.
如图,α∥β,AB∥CD,且A∈α,C∈α,B∈β,D∈β.
求证:AB=CD.
证明:过平行线AB,CD作平面γ,与平面α和β分别相交于AC和BD.
∵α∥β, ∴BD∥AC.
又 AB∥CD, ∴四边形ABCD是平行四边形.
∴ AB=CD.
典例示范 升华提高
例2 求证:夹在两个平行平面间的平行线段相等.
归纳小结 深化认知
问题6 你能从中总结出证明直线与直线平行的一般步骤吗?
回顾反思 领悟提升
课堂小结
直观感知
操作确认
思辨论证
回顾反思 领悟提升
直线与直线平行
直线与平面平行
平面与平面平行
(判定)
(性质 )
(定义 )
( 性质 )
( 判定 )
课堂小结
a
b
α
a
b
α
β
α
a
b
P
β
空间平行关系如何相互转化:
课后训练 巩固拓展
作业练习+教科书习题8.5第8题
同课章节目录
- 第六章 平面向量及其应用
- 6.1 平面向量的概念
- 6.2 平面向量的运算
- 6.3 平面向量基本定理及坐标表示
- 6.4 平面向量的应用
- 第七章 复数
- 7.1 复数的概念
- 7.2 复数的四则运算
- 7.3 * 复数的三角表示
- 第八章 立体几何初步
- 8.1 基本立体图形
- 8.2 立体图形的直观图
- 8.3 简单几何体的表面积与体积
- 8.4 空间点、直线、平面之间的位置关系
- 8.5 空间直线、平面的平行
- 8.6 空间直线、平面的垂直
- 第九章 统计
- 9.1 随机抽样
- 9.2 用样本估计总体
- 9.3 统计分析案例 公司员工
- 第十章 概率
- 10.1 随机事件与概率
- 10.2 事件的相互独立性
- 10.3 频率与概率
