8.3 简单几何体的表面积与体积 课件(共23张PPT)
文档属性
| 名称 | 8.3 简单几何体的表面积与体积 课件(共23张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 9.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-04-17 00:00:00 | ||
图片预览





文档简介
(共23张PPT)
单/击/此/处/添/加/副/标/题/内/容
简单几何体的表面积与体积
要想获得真理和知识,惟有两件武器,那就是清晰的直觉和严格的演绎.
-笛卡尔(法国,1596-1650)
目录/CONTENTS
01
02
03
04
具体实物
基本立体图形
认识结构
图形的度量
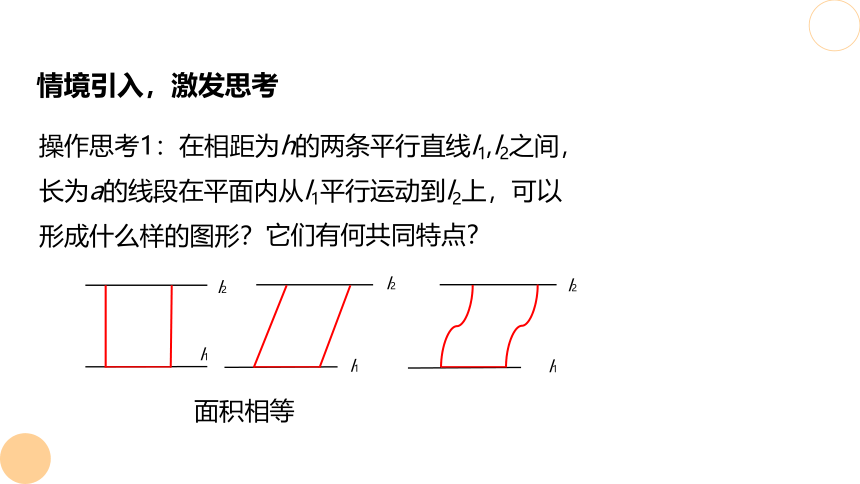
情境引入,激发思考
操作思考1:在相距为h的两条平行直线l1,l2之间,长为a的线段在平面内从l1平行运动到l2上,可以形成什么样的图形?
l2
l1
l2
l1
l2
l1
面积相等
它们有何共同特点?
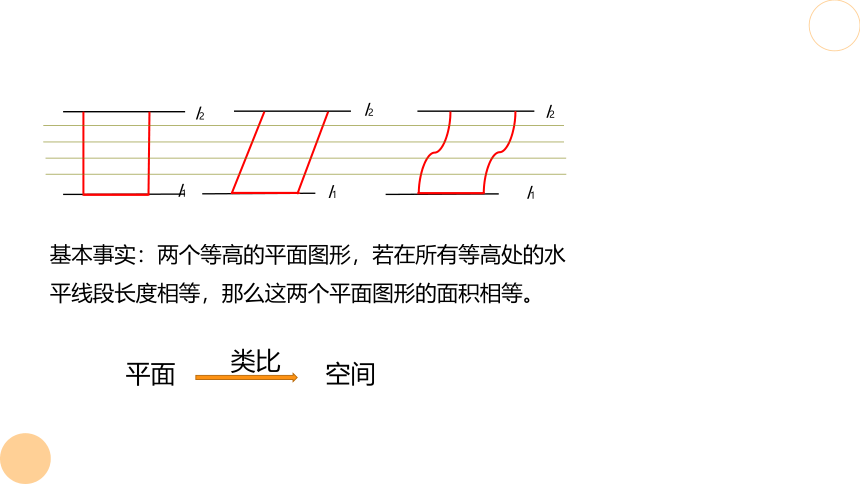
基本事实:两个等高的平面图形,若在所有等高处的水
平线段长度相等,那么这两个平面图形的面积相等。
l2
l1
l2
l1
l2
l1
空间
平面
类比
操作与思考2:同一摞纸,当改变摆放纸的形状时,
它们的体积是否发生变化?
体积:一个几何体所占空间的大小.
体积不变
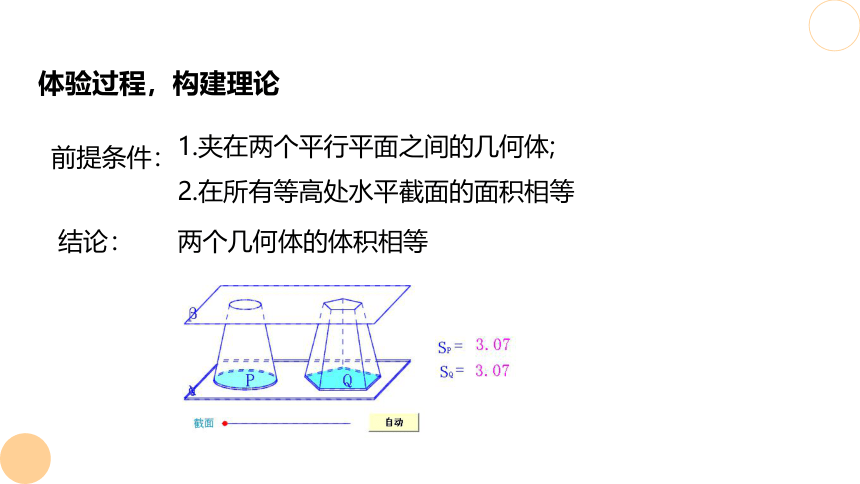
体验过程,构建理论
1.夹在两个平行平面之间的几何体;
2.在所有等高处水平截面的面积相等
两个几何体的体积相等
前提条件:
结论:
祖暅(gèng)原理
幂势既同,则积不容异.
祖暅(456年-536年)
幂:横截面积
势:高
夹在两个平行平面之间的两个几何体,被平行于这两个平面的任意平面所截,如果截得的两个截面的面积总相等,那么这两个几何体的体积相等。
祖冲之(429年-500年)
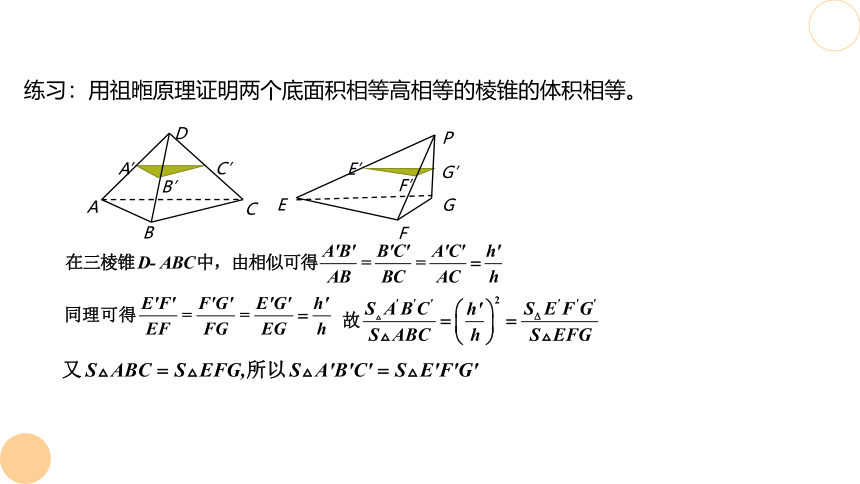
练习:用祖暅原理证明两个底面积相等高相等的棱锥的体积相等。
A
B
C
D
A’
C’
B’
E
F
G
P
E’
F’
G’
思考3:若一个棱柱的底面积为S ,高为h,该棱柱的体积如何表示 ?
h
s
体验过程,构建理论
长方体的体积公式
V=S底h
s
h
s
h
棱柱的体积公式 V=S底h
由祖暅原理得出
h
s
长方体
转化
学生活动1:请小组进行活动探究,三棱锥的体积与它等底等高的三棱柱体的体积之比是多少?为什么?
A
B
A’
C
A’
C’
A
B
C
B’
A
B
C
A’
B’
C’
A
B
C
A’
B’
C’
C
A’
B’
C’
A
B
A’
C
三棱锥的体积公式:
分
割
分
割
对于一般的棱锥
高h
P
A
B
C
D
E
底面面积S
分割
P
A
B
C
D
E
棱锥的体积公式:
学生活动2:类比刚才的学习经验,请同学们自行设计方案推导棱台的体积。其中棱台的上底面积为S’,下底面积为S,高为h,用这三个量表示棱台的体积。
棱台的高是指两底面之间的距离,即从上底面上任意一点向下底面作垂线,这点与垂足之间的距离.
P
方案一:将四棱台补成四棱锥
补形
方案二:将四棱台分割成棱柱与棱锥
分割
尝试推导棱台体积公式
棱台得体积公式
思考4:棱柱、棱锥、棱台的体积公式之间有什么关系?你能用棱柱、棱锥、棱台的结构特征来解释这种关系吗?
P
上底扩大
上底缩小
祖暅原理
补形
分割
S’=S
S’=0
分割
例1:如右图,一个漏斗的上面部分是一个长方体,下面部分是一个四棱锥,两部分的高都是0.5m,公共面ABCD是边长为1m的正方形,那么这个漏斗的容积是多少立方米
A'
B'
C'
D'
A
B
C
D
P
应用公式,巩固新知
解:由题意知
所以这个漏斗的容积
解:依题意可知棱台的高为 (m),所以增加的水量即为棱台的体积
故选C
课堂小结,内化新知
一、知识结构:
二、学习过程:
三、思想方法:
祖暅原理
类比
归纳
操作
证明
猜想
从具体到抽象,从感性到理性
转化与化归 特殊到一般
单/击/此/处/添/加/副/标/题/内/容
简单几何体的表面积与体积
要想获得真理和知识,惟有两件武器,那就是清晰的直觉和严格的演绎.
-笛卡尔(法国,1596-1650)
目录/CONTENTS
01
02
03
04
具体实物
基本立体图形
认识结构
图形的度量
情境引入,激发思考
操作思考1:在相距为h的两条平行直线l1,l2之间,长为a的线段在平面内从l1平行运动到l2上,可以形成什么样的图形?
l2
l1
l2
l1
l2
l1
面积相等
它们有何共同特点?
基本事实:两个等高的平面图形,若在所有等高处的水
平线段长度相等,那么这两个平面图形的面积相等。
l2
l1
l2
l1
l2
l1
空间
平面
类比
操作与思考2:同一摞纸,当改变摆放纸的形状时,
它们的体积是否发生变化?
体积:一个几何体所占空间的大小.
体积不变
体验过程,构建理论
1.夹在两个平行平面之间的几何体;
2.在所有等高处水平截面的面积相等
两个几何体的体积相等
前提条件:
结论:
祖暅(gèng)原理
幂势既同,则积不容异.
祖暅(456年-536年)
幂:横截面积
势:高
夹在两个平行平面之间的两个几何体,被平行于这两个平面的任意平面所截,如果截得的两个截面的面积总相等,那么这两个几何体的体积相等。
祖冲之(429年-500年)
练习:用祖暅原理证明两个底面积相等高相等的棱锥的体积相等。
A
B
C
D
A’
C’
B’
E
F
G
P
E’
F’
G’
思考3:若一个棱柱的底面积为S ,高为h,该棱柱的体积如何表示 ?
h
s
体验过程,构建理论
长方体的体积公式
V=S底h
s
h
s
h
棱柱的体积公式 V=S底h
由祖暅原理得出
h
s
长方体
转化
学生活动1:请小组进行活动探究,三棱锥的体积与它等底等高的三棱柱体的体积之比是多少?为什么?
A
B
A’
C
A’
C’
A
B
C
B’
A
B
C
A’
B’
C’
A
B
C
A’
B’
C’
C
A’
B’
C’
A
B
A’
C
三棱锥的体积公式:
分
割
分
割
对于一般的棱锥
高h
P
A
B
C
D
E
底面面积S
分割
P
A
B
C
D
E
棱锥的体积公式:
学生活动2:类比刚才的学习经验,请同学们自行设计方案推导棱台的体积。其中棱台的上底面积为S’,下底面积为S,高为h,用这三个量表示棱台的体积。
棱台的高是指两底面之间的距离,即从上底面上任意一点向下底面作垂线,这点与垂足之间的距离.
P
方案一:将四棱台补成四棱锥
补形
方案二:将四棱台分割成棱柱与棱锥
分割
尝试推导棱台体积公式
棱台得体积公式
思考4:棱柱、棱锥、棱台的体积公式之间有什么关系?你能用棱柱、棱锥、棱台的结构特征来解释这种关系吗?
P
上底扩大
上底缩小
祖暅原理
补形
分割
S’=S
S’=0
分割
例1:如右图,一个漏斗的上面部分是一个长方体,下面部分是一个四棱锥,两部分的高都是0.5m,公共面ABCD是边长为1m的正方形,那么这个漏斗的容积是多少立方米
A'
B'
C'
D'
A
B
C
D
P
应用公式,巩固新知
解:由题意知
所以这个漏斗的容积
解:依题意可知棱台的高为 (m),所以增加的水量即为棱台的体积
故选C
课堂小结,内化新知
一、知识结构:
二、学习过程:
三、思想方法:
祖暅原理
类比
归纳
操作
证明
猜想
从具体到抽象,从感性到理性
转化与化归 特殊到一般
同课章节目录
- 第六章 平面向量及其应用
- 6.1 平面向量的概念
- 6.2 平面向量的运算
- 6.3 平面向量基本定理及坐标表示
- 6.4 平面向量的应用
- 第七章 复数
- 7.1 复数的概念
- 7.2 复数的四则运算
- 7.3 * 复数的三角表示
- 第八章 立体几何初步
- 8.1 基本立体图形
- 8.2 立体图形的直观图
- 8.3 简单几何体的表面积与体积
- 8.4 空间点、直线、平面之间的位置关系
- 8.5 空间直线、平面的平行
- 8.6 空间直线、平面的垂直
- 第九章 统计
- 9.1 随机抽样
- 9.2 用样本估计总体
- 9.3 统计分析案例 公司员工
- 第十章 概率
- 10.1 随机事件与概率
- 10.2 事件的相互独立性
- 10.3 频率与概率
