人教版六年级下册数学成反比例的量》课件(29张PPT)
文档属性
| 名称 | 人教版六年级下册数学成反比例的量》课件(29张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-04-16 00:00:00 | ||
图片预览








文档简介
(共29张PPT)
成反比例的量
复习
什么是成正比例的量和正比例关系?
两种相关联的量,一种量变化,另一种量也随着变化,如果这两种量中相对应的两个数的比值一定,这两种量就叫做成反比例的量,他们的关系叫做反比例关系。
复习导入
1.什么是成正比例的量
2. 怎样判定两个量是否成正比例?
判断方法:
判断两个量是不是成正比例关系,首先要看这两个量是不是相关联的量,其次看这两个量的比值(商)是不是一定的。
复习导入
3. 判断下面各题中的两种量是否成正比例
⑴长方形的长一定,它的宽和面积
⑵全班人数一定,男生人数和女生人数。
⑶圆的周长和直径。
⑷一个人的年龄和他的身高。
√
√
X
X
判断方法:
判断两个量是不是成正比例关系,首先要看这两个量是不是相关联的量,其次看这两个量的商是不是一定的。
杯子的底面积与水的高度的变化情况如下表。
杯子的底面积/cm
水的高度/cm
10
30
15
20
20
15
30
10
60
5
…
…
把相同体积的水倒入底面积不同的杯子。
(1)表中有哪两种量?
(2)水的高度是怎样随着杯子底面积的大小变化而变化的?
(3)相对应的杯子的底面积与水的高度的乘积分别是多少?
底面积和高度的积(体积)总是一定的,都是300。
10×30=300
15×20=300
20×15=300
30×10=300
60× 5=300
从上往下看,底面积增加,水的高度反而减少。
从下往上看,底面积减少,水的高度反而增加。
(一定)
底面积×高度=水的体积
高度和底面积的变化有什么规律?
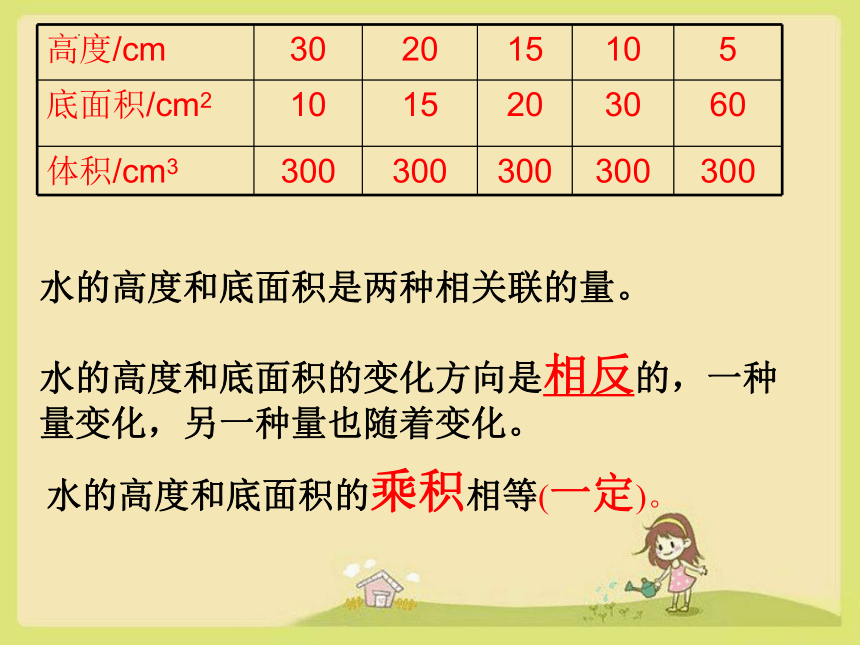
高度/cm 30 20 15 10 5
底面积/cm2 10 15 20 30 60
体积/cm3 300 300 300 300 300
水的高度和底面积是两种相关联的量。
水的高度和底面积的变化方向是相反的,一种量变化,另一种量也随着变化。
水的高度和底面积的乘积相等(一定)。
两种相关联的量,一种量变化,另一种量也随着变化,如果这两种量中相对应的两个数的乘积一定,这两种量就叫做成反比例的量,它们的关系叫做反比例关系。
如果用字母x和y表示两种相关联的量,用k表示它们的积(一定),反比例关系可以用下面的式子表示:
y
x
=k
(一定)
×
想一想,生活中还有哪些成反比例的量?
判断两个量是不是成 反比例关系,首先要看这两个量是不是相关联的量,其次看这两个量的积是不是一定的。
判断方法
做一做
(1)表中有哪两种量?它们是不是相关联的量?
表中有每天运的吨数和需要的天数两种量。
(2)写出几组这两种量中相对应的两个数的积,并比
较积的大小。
300 ×1 =300
150 × 2=300
100 × 3=300
每天运的吨数
需 要 的 天 数
300
6
1
150
2
150
100
75
60
50
3
4
5
它们是相关联的量。
75 ×4 =300
60 × 5=300
50 × 6=300
(积相等)
做一做
运一批货物,每天运的吨数和需要的天数如下表。
根据表回答下面的问题。
(3)说明这个积所表示的意义。
这个积表示这批货物的总吨数。
(4)表中相关联的两种量成反比例吗?为什么?
每天运的吨数
需 要 的 天 数
300
6
1
150
2
150
100
75
60
50
3
4
5
每天运的吨数和需要的天数成反比例。
每天运的吨数×需要的天数=货物总吨数(一定)
每天运的吨数和需要的天数成反比例。
因为:每天运的吨数和需要的天数是相关联的量
所以:
我学会了!
1、判定两个量是否成反比例,
主要看它们的( )
是否一定。
所以( )和( )是成反比例的量。
2、全班人数一定,每组的人数和组数。
( )和( )是相关联的量。
每组的人数
组数
每组的人数×组数=全班人数(一定)
每组的人数
组数
乘积
巩固练习
判断下面每题中的两种量是不是成反比例,并说明理由。
(1)工作总量一定,工作效率和工作时间。
(2)总人数一定,每行人数和行数。
(3)用一根绳子围成长方形,长和宽。
(4)一本故事书,每天读的页数和天数。
(5)圆锥的体积一定,底面积和高。
正比例 反比例
相同点
不同点
都是两种相关联的量,
一种量随着另一种量变化。
1.变化的方向相同,一种量扩大或缩小,另一种量也扩大或缩小。
1.变化的方向相反,一种量扩大或缩小,另一种量反而缩小或扩大。
2.相对应的每两个数的比值是一定的。
2.相对应的每两个数的乘积是一定的。
3.关系式:
y/x=k(一定)
3.关系式:
x × y = k(一定)
两种量
不相关联
相关联
加的关系
减的关系
乘的关系
除的关系
→不成比例
→不成比例
→不成比例
积一定
商一定
→成反比例
→成正比例
每块地砖的面积和数量是两种相关联的量,因为每块地砖的面积×数量=教室面积(一定),所以每块地砖的面积和数量成反比例。
9×6=54(m2)=540000(cm2)
900×600=540000
1800×300=540000
3600×150=540000
9×6=54(m2)=540000(cm2)
每块地砖的面积和数量是两种相关联的量,因为每块地砖的面积×数量=教室面积(一定),所以每块地砖的面积和数量成反比例。
9×6=54(m2)=540000(cm2)
900×600=540000
1800×300=540000
3600×150=540000
9×6=54(m2)=540000(cm2)
每块地砖的面积和数量是两种相关联的量,因为每块地砖的面积×数量=教室面积(一定),所以每块地砖的面积和数量成反比例。
9×6=54(m2)=540000(cm2)
900×600=540000
1800×300=540000
3600×150=540000
9×6=54(m2)=540000(cm2)
每块地砖的面积和数量是两种相关联的量,因为每块地砖的面积×数量=教室面积(一定),所以每块地砖的面积和数量成反比例。
9×6=54(m2)=540000(cm2)
900×600=540000
1800×300=540000
3600×150=540000
9×6=54(m2)=540000(cm2)
每瓶容量和数量是两种相关联的量,因为每瓶容量×数量=醋的总量(一定),所以每瓶容量和数量成反比例。
50
100
0.25
12
(1)学校食堂新进一批煤,每天的用煤量与使用天数。
9.判断下面每题中的两个量是否成反比例,并说明理由。
每天的用煤量与使用天数是两种相关联的量,因为每天用煤量×使用天数=煤的总量(一定),所以每天的用煤量与使用天数成反比例。
(2)全班的人数一定,每组的人数和组数。
每组的人数和组数是两种相关联的量,因为每组的人数×组数=全班的人数(一定),所以每组的人数和组数成反比例。
(3)圆柱体积一定,圆柱的底面积和高。
圆柱的底面积和高是两种相关联的量,因为圆柱的底面积×高=圆柱体积(一定),所以圆柱的底面积和高成反比例。
(4)书的总册数一定,每包的册数和包数。
每包的册数和包数是两种相关联的量,因为每包的册数×包数=书的总册数(一定),所以每包的册数和包数成反比例。
(5)在一块菜地上种的黄瓜和西红柿的面积。
黄瓜的种植面积和西红柿的种植面积是两种相关联的量,因为黄瓜的种植面积+西红柿的种植面积=这块地的总面积(一定),也就是和一定,所以黄瓜的种植面积和西红柿的种植面积不成比例。
1, 7﹕ x = y﹕15,x 和 y成什么比例关系?
2,小明从家到学校行走的路程和剩下的路程是成反 比例吗?为什么?
3, 甲数和乙数互为倒数,甲数和乙数成什么比例关系?
课外思考
4、已知A×B=C。(A、B、C均不为0)
当A一定时,B和C成什么比例?
当B一定时,A和C成什么比例?
当C一定时,A和B成什么比例?
课外思考
生活中还有哪些
成反比例的量?
成反比例的量
复习
什么是成正比例的量和正比例关系?
两种相关联的量,一种量变化,另一种量也随着变化,如果这两种量中相对应的两个数的比值一定,这两种量就叫做成反比例的量,他们的关系叫做反比例关系。
复习导入
1.什么是成正比例的量
2. 怎样判定两个量是否成正比例?
判断方法:
判断两个量是不是成正比例关系,首先要看这两个量是不是相关联的量,其次看这两个量的比值(商)是不是一定的。
复习导入
3. 判断下面各题中的两种量是否成正比例
⑴长方形的长一定,它的宽和面积
⑵全班人数一定,男生人数和女生人数。
⑶圆的周长和直径。
⑷一个人的年龄和他的身高。
√
√
X
X
判断方法:
判断两个量是不是成正比例关系,首先要看这两个量是不是相关联的量,其次看这两个量的商是不是一定的。
杯子的底面积与水的高度的变化情况如下表。
杯子的底面积/cm
水的高度/cm
10
30
15
20
20
15
30
10
60
5
…
…
把相同体积的水倒入底面积不同的杯子。
(1)表中有哪两种量?
(2)水的高度是怎样随着杯子底面积的大小变化而变化的?
(3)相对应的杯子的底面积与水的高度的乘积分别是多少?
底面积和高度的积(体积)总是一定的,都是300。
10×30=300
15×20=300
20×15=300
30×10=300
60× 5=300
从上往下看,底面积增加,水的高度反而减少。
从下往上看,底面积减少,水的高度反而增加。
(一定)
底面积×高度=水的体积
高度和底面积的变化有什么规律?
高度/cm 30 20 15 10 5
底面积/cm2 10 15 20 30 60
体积/cm3 300 300 300 300 300
水的高度和底面积是两种相关联的量。
水的高度和底面积的变化方向是相反的,一种量变化,另一种量也随着变化。
水的高度和底面积的乘积相等(一定)。
两种相关联的量,一种量变化,另一种量也随着变化,如果这两种量中相对应的两个数的乘积一定,这两种量就叫做成反比例的量,它们的关系叫做反比例关系。
如果用字母x和y表示两种相关联的量,用k表示它们的积(一定),反比例关系可以用下面的式子表示:
y
x
=k
(一定)
×
想一想,生活中还有哪些成反比例的量?
判断两个量是不是成 反比例关系,首先要看这两个量是不是相关联的量,其次看这两个量的积是不是一定的。
判断方法
做一做
(1)表中有哪两种量?它们是不是相关联的量?
表中有每天运的吨数和需要的天数两种量。
(2)写出几组这两种量中相对应的两个数的积,并比
较积的大小。
300 ×1 =300
150 × 2=300
100 × 3=300
每天运的吨数
需 要 的 天 数
300
6
1
150
2
150
100
75
60
50
3
4
5
它们是相关联的量。
75 ×4 =300
60 × 5=300
50 × 6=300
(积相等)
做一做
运一批货物,每天运的吨数和需要的天数如下表。
根据表回答下面的问题。
(3)说明这个积所表示的意义。
这个积表示这批货物的总吨数。
(4)表中相关联的两种量成反比例吗?为什么?
每天运的吨数
需 要 的 天 数
300
6
1
150
2
150
100
75
60
50
3
4
5
每天运的吨数和需要的天数成反比例。
每天运的吨数×需要的天数=货物总吨数(一定)
每天运的吨数和需要的天数成反比例。
因为:每天运的吨数和需要的天数是相关联的量
所以:
我学会了!
1、判定两个量是否成反比例,
主要看它们的( )
是否一定。
所以( )和( )是成反比例的量。
2、全班人数一定,每组的人数和组数。
( )和( )是相关联的量。
每组的人数
组数
每组的人数×组数=全班人数(一定)
每组的人数
组数
乘积
巩固练习
判断下面每题中的两种量是不是成反比例,并说明理由。
(1)工作总量一定,工作效率和工作时间。
(2)总人数一定,每行人数和行数。
(3)用一根绳子围成长方形,长和宽。
(4)一本故事书,每天读的页数和天数。
(5)圆锥的体积一定,底面积和高。
正比例 反比例
相同点
不同点
都是两种相关联的量,
一种量随着另一种量变化。
1.变化的方向相同,一种量扩大或缩小,另一种量也扩大或缩小。
1.变化的方向相反,一种量扩大或缩小,另一种量反而缩小或扩大。
2.相对应的每两个数的比值是一定的。
2.相对应的每两个数的乘积是一定的。
3.关系式:
y/x=k(一定)
3.关系式:
x × y = k(一定)
两种量
不相关联
相关联
加的关系
减的关系
乘的关系
除的关系
→不成比例
→不成比例
→不成比例
积一定
商一定
→成反比例
→成正比例
每块地砖的面积和数量是两种相关联的量,因为每块地砖的面积×数量=教室面积(一定),所以每块地砖的面积和数量成反比例。
9×6=54(m2)=540000(cm2)
900×600=540000
1800×300=540000
3600×150=540000
9×6=54(m2)=540000(cm2)
每块地砖的面积和数量是两种相关联的量,因为每块地砖的面积×数量=教室面积(一定),所以每块地砖的面积和数量成反比例。
9×6=54(m2)=540000(cm2)
900×600=540000
1800×300=540000
3600×150=540000
9×6=54(m2)=540000(cm2)
每块地砖的面积和数量是两种相关联的量,因为每块地砖的面积×数量=教室面积(一定),所以每块地砖的面积和数量成反比例。
9×6=54(m2)=540000(cm2)
900×600=540000
1800×300=540000
3600×150=540000
9×6=54(m2)=540000(cm2)
每块地砖的面积和数量是两种相关联的量,因为每块地砖的面积×数量=教室面积(一定),所以每块地砖的面积和数量成反比例。
9×6=54(m2)=540000(cm2)
900×600=540000
1800×300=540000
3600×150=540000
9×6=54(m2)=540000(cm2)
每瓶容量和数量是两种相关联的量,因为每瓶容量×数量=醋的总量(一定),所以每瓶容量和数量成反比例。
50
100
0.25
12
(1)学校食堂新进一批煤,每天的用煤量与使用天数。
9.判断下面每题中的两个量是否成反比例,并说明理由。
每天的用煤量与使用天数是两种相关联的量,因为每天用煤量×使用天数=煤的总量(一定),所以每天的用煤量与使用天数成反比例。
(2)全班的人数一定,每组的人数和组数。
每组的人数和组数是两种相关联的量,因为每组的人数×组数=全班的人数(一定),所以每组的人数和组数成反比例。
(3)圆柱体积一定,圆柱的底面积和高。
圆柱的底面积和高是两种相关联的量,因为圆柱的底面积×高=圆柱体积(一定),所以圆柱的底面积和高成反比例。
(4)书的总册数一定,每包的册数和包数。
每包的册数和包数是两种相关联的量,因为每包的册数×包数=书的总册数(一定),所以每包的册数和包数成反比例。
(5)在一块菜地上种的黄瓜和西红柿的面积。
黄瓜的种植面积和西红柿的种植面积是两种相关联的量,因为黄瓜的种植面积+西红柿的种植面积=这块地的总面积(一定),也就是和一定,所以黄瓜的种植面积和西红柿的种植面积不成比例。
1, 7﹕ x = y﹕15,x 和 y成什么比例关系?
2,小明从家到学校行走的路程和剩下的路程是成反 比例吗?为什么?
3, 甲数和乙数互为倒数,甲数和乙数成什么比例关系?
课外思考
4、已知A×B=C。(A、B、C均不为0)
当A一定时,B和C成什么比例?
当B一定时,A和C成什么比例?
当C一定时,A和B成什么比例?
课外思考
生活中还有哪些
成反比例的量?
