沪教版八年级数学下册试题 一次函数(提高练习)(含解析)
文档属性
| 名称 | 沪教版八年级数学下册试题 一次函数(提高练习)(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 128.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-04-17 09:43:11 | ||
图片预览



文档简介
一次函数(提高练习)
一、单选题
1.下列关系式中,y是x的一次函数的有( )
①y=2x﹣3 ②y=﹣③y=+x④y=10﹣1﹣25x⑤y=+1.
A.1个 B.2个 C.3个 D.4个
2.已知函数y=(k﹣1)x|k|+3是一次函数,则k=( )
A.1 B.﹣1 C.0 D.±1
3.已知正比例函数y=kx(k≠0)的函数值y随x的增大而减小,则一次函数y=﹣kx+k的图象大致是( )
A. B.
C. D.
4.已知A(x1,y1)B(x2,y2)在正比例函数上y=﹣x的图象上,若y1<y2,则x1与x2的关系为( )
A.x1>x2 B.x1=x2 C.x1<x2 D.无法确定
5.y关于x的函数y=(2m﹣1)x﹣3m+2的图象经过一个定点,这个点的坐标是( )
A.(3,1) B.(0,2) C.() D.()
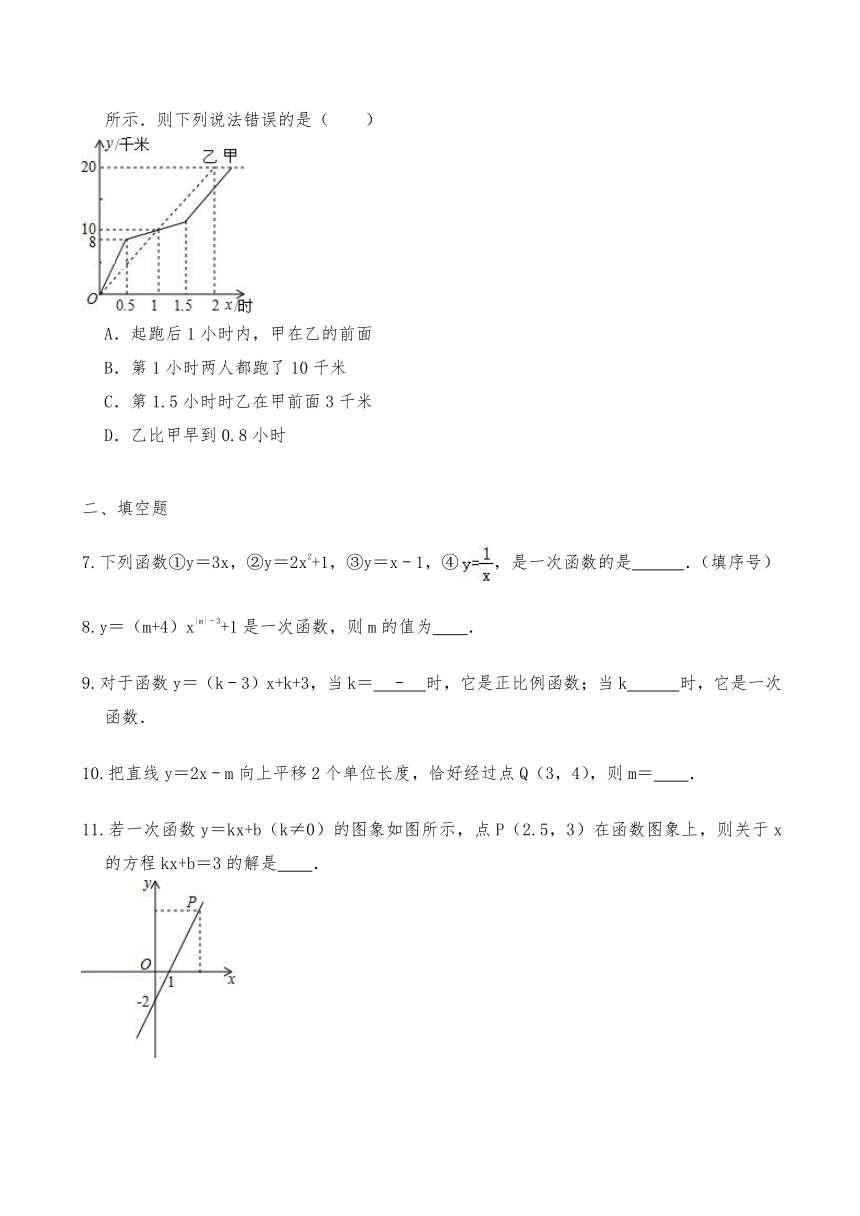
6.在全民健身越野赛中,甲、乙两位选手的行程y(千米)随时间x(小时)变化的图象如图所示.则下列说法错误的是( )
A.起跑后1小时内,甲在乙的前面
B.第1小时两人都跑了10千米
C.第1.5小时时乙在甲前面3千米
D.乙比甲早到0.8小时
二、填空题
7.下列函数①y=3x,②y=2x2+1,③y=x﹣1,④,是一次函数的是 .(填序号)
8.y=(m+4)x|m|﹣3+1是一次函数,则m的值为 .
9.对于函数y=(k﹣3)x+k+3,当k= ﹣ 时,它是正比例函数;当k 时,它是一次函数.
10.把直线y=2x﹣m向上平移2个单位长度,恰好经过点Q(3,4),则m= .
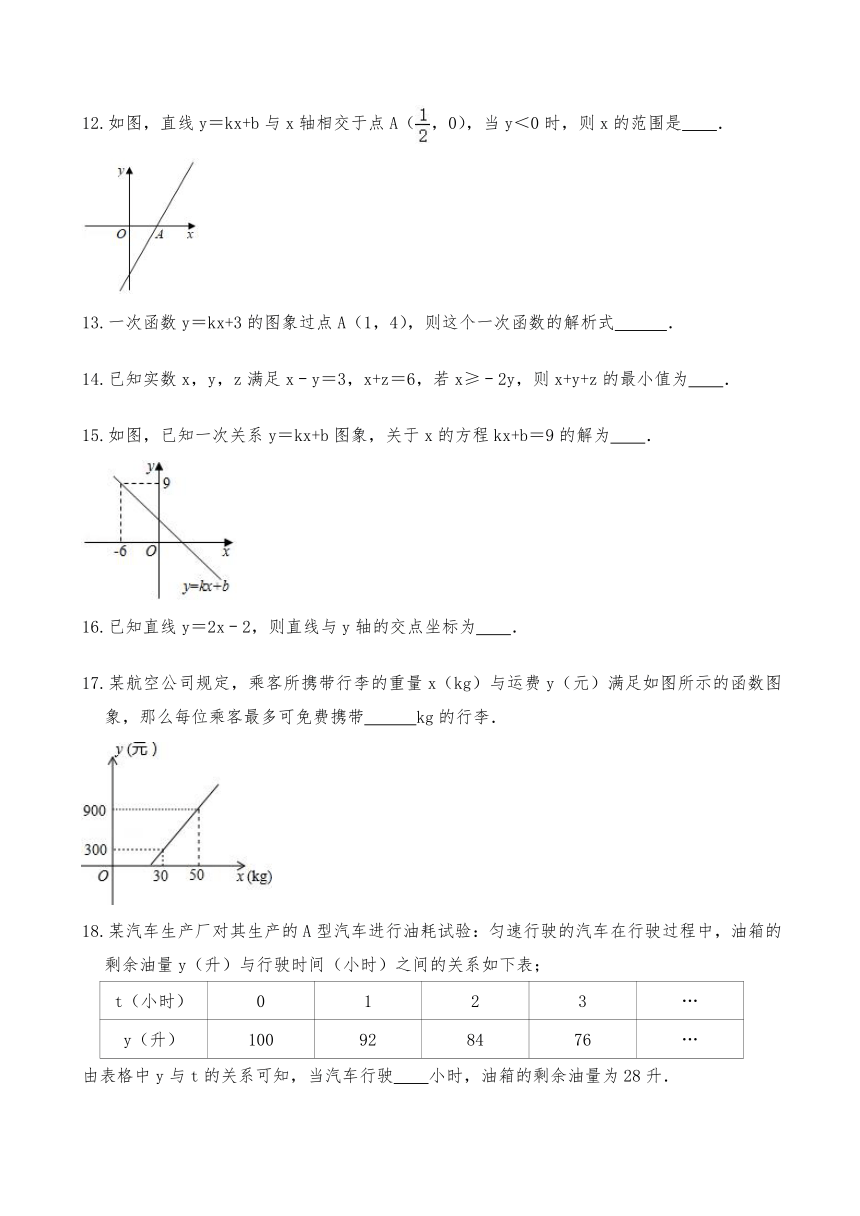
11.若一次函数y=kx+b(k≠0)的图象如图所示,点P(2.5,3)在函数图象上,则关于x的方程kx+b=3的解是 .
12.如图,直线y=kx+b与x轴相交于点A(,0),当y<0时,则x的范围是 .
13.一次函数y=kx+3的图象过点A(1,4),则这个一次函数的解析式 .
14.已知实数x,y,z满足x﹣y=3,x+z=6,若x≥﹣2y,则x+y+z的最小值为 .
15.如图,已知一次关系y=kx+b图象,关于x的方程kx+b=9的解为 .
16.已知直线y=2x﹣2,则直线与y轴的交点坐标为 .
17.某航空公司规定,乘客所携带行李的重量x(kg)与运费y(元)满足如图所示的函数图象,那么每位乘客最多可免费携带 kg的行李.
18.某汽车生产厂对其生产的A型汽车进行油耗试验:匀速行驶的汽车在行驶过程中,油箱的剩余油量y(升)与行驶时间(小时)之间的关系如下表;
t(小时) 0 1 2 3 …
y(升) 100 92 84 76 …
由表格中y与t的关系可知,当汽车行驶 小时,油箱的剩余油量为28升.
三、解答题
19.已知,若函数y=(m﹣1)+3是关于x的一次函数
(1)求m的值,并写出解析式.
(2)判断点(1,2)是否在此函数图象上,说明理由.
20.已知y﹣1与2x+3成正比例.
(1)y是关于x的一次函数吗?请说明理由;
(2)如果当x=时,y=0,求y关于x的函数表达式.
21.已知直线y=kx+2与y轴交于点A.将点A向右平移2个单位,再向上平移1个单位,得到点B.
(1)求点A,B坐标;
(2)点B关于x轴的对称点为点C,若直线y=kx+2与线段BC有公共点,求k的取值范围.
22.已知直线y=kx+b的图象经过点(2,4)和点(﹣2,﹣2).
(1)求b的值;
(2)求关于x的方程kx+b=0的解;
(3)若(x1,y1)、(x2,y2)为直线上两点,且x1<x2,试比较y1、y2的大小.
23.如图,点A的坐标为(﹣,0),点B的坐标为(0,3).
(1)求过A,B两点直线的函数表达式;
(2)过B点作直线BP与x轴交于点P,且使OP=2OA,求△ABP的面积.
24.甲、乙两车从A城出发匀速行驶至B城,在整个行驶过程中,甲、乙两车离开A城的距离y(千米)与行驶时间x(小时)之间的函数关系如图所示,已知甲对应的函数关系式为y=60x,根据图象提供的信息,解决下列问题:
(1)求乙离开A城的距离y与x的关系式;
(2)求乙出发后几小时追上甲车?
25.某商场新上市一款毛衣,进价是40元,当售价为80元,一天可以销售20件.若售价每降价1元,则每天可以多卖2件.设售价为x元,当天的销售量为y件.
(1)销售量y与售价x之间的函数表达式为 ﹣ ;
(2)在尽可能增大销售量的前提下,问这款毛衣降价后的售价为多少元时,商场当天可获利1200元?
答案
一、单选题
1.D
【分析】根据一次函数的定义条件进行逐一判断即可.
【解答】解:y是x的一次函数的有①y=2x﹣3、②y=﹣、③y=+x、④y=10﹣1﹣25x,
故选:D.
2.B
【分析】一次函数y=kx+b的定义条件是:k、b为常数,k≠0,自变量次数为1.则x的次数是1,且系数不等于0,据此即可求解.
【解答】解:根据题意得:,
解得:k=﹣1.
故选:B.
3.B
【分析】由于正比例函数y=kx(k≠0)函数值随x的增大而增大,可得k<0,﹣k>0,然后,判断一次函数y=﹣kx+k的图象经过象限即可;
【解答】解:∵正比例函数y=kx(k≠0)函数值随x的增大而增大,
∴k<0,
∴﹣k>0,
∴一次函数y=﹣kx+k的图象经过一、三、四象限;
故选:B.
4.A
【分析】先根据一次函数的性质得出y随x的增大而减小,再得出答案即可.
【解答】解:∵正比例函数上y=﹣x中﹣<0,y随x的增大而减小,
又∵A(x1,y1)B(x2,y2)在正比例函数上y=﹣x的图象上,
∴若y1<y2,则x1与x2的关系为x1>x2,
故选:A.
5.C
【分析】y=(2m﹣1)x﹣3m+2=m(2x﹣3)﹣x+2,当2x﹣3=0时,即:x=时,图象过定点,即可求解.
【解答】解:y=(2m﹣1)x﹣3m+2=m(2x﹣3)﹣x+2,
当2x﹣3=0时,即:x=时,图象过定点,
则定点坐标为(,),
故选:C.
6.D
【分析】根据函数图象和图象中的数据可以判断各个选项中的说法是否正确,从而可以解答本题.
【解答】解:由图象可得,
起跑后1小时内,甲在乙的前面,故选项A正确;
第1小时两人相遇,都跑了10千米,故选项B正确;
乙的速度为:20÷2=10(千米/时),
∴第1.5小时,乙跑了15千米;
∵甲在0.5h~1h的速度为=4(千米),
∴甲在第1.5小时,其行程为8+4×(1.5﹣0.5)=12千米,
∴第1.5小时时乙在甲前面3千米,
故选项C正确;
甲到终点的时间不能确定,故选项D说法错误.
故选:D.
二、填空题
7.①③
【分析】利用一般地,形如y=kx+b(k≠0,k、b是常数)的函数,叫做一次函数,进而判断得出答案.
【解答】解:函数①y=3x,②y=2x2+1,③y=x﹣1,④中,是一次函数的是:①③.
故答案为:①③.
8.4
【分析】直接利用一次函数的定义分析得出答案.
【解答】解:∵y=(m+4)x|m|﹣3+1是一次函数,
∴|m|﹣3=1,m+4≠0,
解得:m=4.
故答案为:4.
9.-3 ≠3
【分析】根据形如y=kx(k是常数,k≠0)的函数叫做正比例函数,形如y=kx+b(k≠0,k、b是常数)的函数,叫做一次函数进行分析即可.
【解答】解:由题意得:k+3=0,
解得:k=﹣3;
k﹣3≠0,
解得:k≠3,
故答案为:k=﹣3,k≠3.
10.4
【分析】向上平移2个单位长度后直线的解析式为y=2x﹣m+2,又该直线经过点Q(3,4),将点代入直线即可求出答案.
【解答】解:直线y=2x﹣m的图象向上平移2个单位长度后的解析式为:y=2x﹣m+2,
将点(3,4)代入y=2x﹣m+2,得4=6﹣m+2,
解得:m=4,
故答案为:4.
11.x=2.5
【分析】观察图象找到当y=3时x的值即为本题的答案.
【解答】解:观察函数的图象知:y=kx+b的图象经过点P(2.5,3),
即当x=2.5时y=kx+b=3,
所以关于x的方程kx+b=3的解为x=2.5,
故答案为:x=2.5.
12.
【分析】当y<0时,图象在x轴下方,然后再结合图象可得答案.
【解答】解:∵直线y=kx+b与x轴相交于点A(,0),
∴当y<0时,x<,
故答案为:x.
13.y=x+3
【分析】把点A的坐标代入一次函数解析式,列出关于系数k的方程k+3=4,通过解该方程可以求得k的值.
【解答】解:由题意,得
k+3=4,
解得,k=1,
所以,该一次函数的解析式是:y=x+3,
故答案为y=x+3
14.5
【分析】根据x﹣y=3,x+z=6,可以用含x的代数式表示出y和z,然后根据x≥﹣2y,可以得到x的取值范围,从而可以求得所求式子的最小值.
【解答】解:∵x﹣y=3,x+z=6,
∴y=x﹣3,z=6﹣x,
∴x+y+z=x+x﹣3+6﹣x=x+3,
∵x≥﹣2y,
∴x≥﹣2(x﹣3),
解得,x≥2,
∴当x=2时,x+y+z取得最小值,此时x+y+z=2+3=5,
故答案为:5.
15.x=-6
【分析】根据图象:得到当y=9时,x=﹣6,由此可以求得方程kx+b=9的解.
【解答】解:∵如图,一次关系y=kx+b图象经过点(﹣6,9)
∴当y=9时,x=﹣6,
即方程kx+b=9的解是x=﹣6.
故答案是:x=﹣6.
16.(0,-2)
【分析】利用一次函数图象上点的坐标特征,可求出该直线与y轴的交点坐标.
【解答】解:∵一次函数的解析式为y=2x﹣2.
当x=0时,y=2x﹣2=﹣2,
∴直线与y轴的交点坐标为(0,﹣2),
故答案为(0,﹣2).
17.20
【分析】设乘客所携带行李的重量x(kg)与运费y(元)之间的函数关系式为y=kx+b,由待定系数法求出其解即可.
【解答】解:设乘客所携带行李的重量x(kg)与运费y(元)之间的函数关系式为y=kx+b,由题意,得
,
解得:,
则y=30x﹣600.
当y=0时,
30x﹣600=0,
解得:x=20.
故答案为:20.
18.9
【分析】由表格可知,开始油箱中的油为100L,每行驶1小时,油量减少8L,据此可得y与t的关系式.
【解答】解:由题意可得:y=100﹣8t,
当y=28时,28=100﹣8t
解得:t=9.
故答案为:9.
三、解答题
19.解:(1)由y=(m﹣1)+3是关于x的一次函数,得
,解得m=﹣1,
函数解析式为y=﹣2x+3
(2)将x=1代入解析式得y=1≠2,
故不在函数图象上.
20.解:(1)设y﹣1=k(2x+3),
∴y=2kx+3k+1,
∴y是关于x的一次函数;
(2)把x=,y=0代入得﹣k+3k+1=0,解得k=3,
∴y关于x的函数表达式为y=6x+10.
21.解:(1)∵直线y=kx+2与y轴交于点A,
∴A(0,2),
∵将点A向右平移2个单位,再向上平移1个单位,得到点B.
∴B(2,3);
(2)∵点B关于x轴的对称点为点C,B(2,3),
∴C(2,﹣3),
把B(2,3)代入y=kx+2得,3=2k+2,解得k=,
把C(2,﹣3)代入y=kx+2得,﹣3=2k+2,解得k=﹣,
∴若直线y=kx+2与线段BC有公共点,k的取值范围是﹣≤k≤.
22.解:(1)根据题意得,解得,
即b的值为1;
(2)一次函数解析式为y=x+1,
当y=0时,x+1=0,解得x=﹣;
(3)∵k=>0,
∴y随x的增大而增大,
∵x1<x2,
∴y1<y2.
23.解:(1)设过A,B两点的直线解析式为y=ax+b(a≠0),则根据题意,得,
解得,,
则过A,B两点的直线解析式为y=2x+3;
(2)设P点坐标为(x,0),依题意得x=±3,所以P点坐标分别为P1(3,0),P2(﹣3,0).
==,
=×(3﹣)×3=,
所以,△ABP的面积为或.
24.解:(1)设乙对应的函数关系式为y=kx+b
将点(4,300),(1,0)代入y=kx+b得:
解得:,
∴乙对应的函数关系式y=100x﹣100;
(2)易得甲车对应的函数解析式为y=60x,
联立,
解得:,2.5﹣1=1.5(小时),
∴乙车出发后1.5小时追上甲车.
25.解:(1)设售价为x元,
则平均每月的销售量y(件)与x满足的函数关系式为:y=20+2(80﹣x),
化简整理,得y=﹣2x+180;
故答案是:y=﹣2x+180;
(2)根据题意,得
(x﹣40)(﹣2x+180)=1200,
解得x1=70,x2=60.
因为是尽可能增大销售量,所以x=60符合题意.
答:这款毛衣降价后的售价为60元时,商场当天可获利1200元.
一、单选题
1.下列关系式中,y是x的一次函数的有( )
①y=2x﹣3 ②y=﹣③y=+x④y=10﹣1﹣25x⑤y=+1.
A.1个 B.2个 C.3个 D.4个
2.已知函数y=(k﹣1)x|k|+3是一次函数,则k=( )
A.1 B.﹣1 C.0 D.±1
3.已知正比例函数y=kx(k≠0)的函数值y随x的增大而减小,则一次函数y=﹣kx+k的图象大致是( )
A. B.
C. D.
4.已知A(x1,y1)B(x2,y2)在正比例函数上y=﹣x的图象上,若y1<y2,则x1与x2的关系为( )
A.x1>x2 B.x1=x2 C.x1<x2 D.无法确定
5.y关于x的函数y=(2m﹣1)x﹣3m+2的图象经过一个定点,这个点的坐标是( )
A.(3,1) B.(0,2) C.() D.()
6.在全民健身越野赛中,甲、乙两位选手的行程y(千米)随时间x(小时)变化的图象如图所示.则下列说法错误的是( )
A.起跑后1小时内,甲在乙的前面
B.第1小时两人都跑了10千米
C.第1.5小时时乙在甲前面3千米
D.乙比甲早到0.8小时
二、填空题
7.下列函数①y=3x,②y=2x2+1,③y=x﹣1,④,是一次函数的是 .(填序号)
8.y=(m+4)x|m|﹣3+1是一次函数,则m的值为 .
9.对于函数y=(k﹣3)x+k+3,当k= ﹣ 时,它是正比例函数;当k 时,它是一次函数.
10.把直线y=2x﹣m向上平移2个单位长度,恰好经过点Q(3,4),则m= .
11.若一次函数y=kx+b(k≠0)的图象如图所示,点P(2.5,3)在函数图象上,则关于x的方程kx+b=3的解是 .
12.如图,直线y=kx+b与x轴相交于点A(,0),当y<0时,则x的范围是 .
13.一次函数y=kx+3的图象过点A(1,4),则这个一次函数的解析式 .
14.已知实数x,y,z满足x﹣y=3,x+z=6,若x≥﹣2y,则x+y+z的最小值为 .
15.如图,已知一次关系y=kx+b图象,关于x的方程kx+b=9的解为 .
16.已知直线y=2x﹣2,则直线与y轴的交点坐标为 .
17.某航空公司规定,乘客所携带行李的重量x(kg)与运费y(元)满足如图所示的函数图象,那么每位乘客最多可免费携带 kg的行李.
18.某汽车生产厂对其生产的A型汽车进行油耗试验:匀速行驶的汽车在行驶过程中,油箱的剩余油量y(升)与行驶时间(小时)之间的关系如下表;
t(小时) 0 1 2 3 …
y(升) 100 92 84 76 …
由表格中y与t的关系可知,当汽车行驶 小时,油箱的剩余油量为28升.
三、解答题
19.已知,若函数y=(m﹣1)+3是关于x的一次函数
(1)求m的值,并写出解析式.
(2)判断点(1,2)是否在此函数图象上,说明理由.
20.已知y﹣1与2x+3成正比例.
(1)y是关于x的一次函数吗?请说明理由;
(2)如果当x=时,y=0,求y关于x的函数表达式.
21.已知直线y=kx+2与y轴交于点A.将点A向右平移2个单位,再向上平移1个单位,得到点B.
(1)求点A,B坐标;
(2)点B关于x轴的对称点为点C,若直线y=kx+2与线段BC有公共点,求k的取值范围.
22.已知直线y=kx+b的图象经过点(2,4)和点(﹣2,﹣2).
(1)求b的值;
(2)求关于x的方程kx+b=0的解;
(3)若(x1,y1)、(x2,y2)为直线上两点,且x1<x2,试比较y1、y2的大小.
23.如图,点A的坐标为(﹣,0),点B的坐标为(0,3).
(1)求过A,B两点直线的函数表达式;
(2)过B点作直线BP与x轴交于点P,且使OP=2OA,求△ABP的面积.
24.甲、乙两车从A城出发匀速行驶至B城,在整个行驶过程中,甲、乙两车离开A城的距离y(千米)与行驶时间x(小时)之间的函数关系如图所示,已知甲对应的函数关系式为y=60x,根据图象提供的信息,解决下列问题:
(1)求乙离开A城的距离y与x的关系式;
(2)求乙出发后几小时追上甲车?
25.某商场新上市一款毛衣,进价是40元,当售价为80元,一天可以销售20件.若售价每降价1元,则每天可以多卖2件.设售价为x元,当天的销售量为y件.
(1)销售量y与售价x之间的函数表达式为 ﹣ ;
(2)在尽可能增大销售量的前提下,问这款毛衣降价后的售价为多少元时,商场当天可获利1200元?
答案
一、单选题
1.D
【分析】根据一次函数的定义条件进行逐一判断即可.
【解答】解:y是x的一次函数的有①y=2x﹣3、②y=﹣、③y=+x、④y=10﹣1﹣25x,
故选:D.
2.B
【分析】一次函数y=kx+b的定义条件是:k、b为常数,k≠0,自变量次数为1.则x的次数是1,且系数不等于0,据此即可求解.
【解答】解:根据题意得:,
解得:k=﹣1.
故选:B.
3.B
【分析】由于正比例函数y=kx(k≠0)函数值随x的增大而增大,可得k<0,﹣k>0,然后,判断一次函数y=﹣kx+k的图象经过象限即可;
【解答】解:∵正比例函数y=kx(k≠0)函数值随x的增大而增大,
∴k<0,
∴﹣k>0,
∴一次函数y=﹣kx+k的图象经过一、三、四象限;
故选:B.
4.A
【分析】先根据一次函数的性质得出y随x的增大而减小,再得出答案即可.
【解答】解:∵正比例函数上y=﹣x中﹣<0,y随x的增大而减小,
又∵A(x1,y1)B(x2,y2)在正比例函数上y=﹣x的图象上,
∴若y1<y2,则x1与x2的关系为x1>x2,
故选:A.
5.C
【分析】y=(2m﹣1)x﹣3m+2=m(2x﹣3)﹣x+2,当2x﹣3=0时,即:x=时,图象过定点,即可求解.
【解答】解:y=(2m﹣1)x﹣3m+2=m(2x﹣3)﹣x+2,
当2x﹣3=0时,即:x=时,图象过定点,
则定点坐标为(,),
故选:C.
6.D
【分析】根据函数图象和图象中的数据可以判断各个选项中的说法是否正确,从而可以解答本题.
【解答】解:由图象可得,
起跑后1小时内,甲在乙的前面,故选项A正确;
第1小时两人相遇,都跑了10千米,故选项B正确;
乙的速度为:20÷2=10(千米/时),
∴第1.5小时,乙跑了15千米;
∵甲在0.5h~1h的速度为=4(千米),
∴甲在第1.5小时,其行程为8+4×(1.5﹣0.5)=12千米,
∴第1.5小时时乙在甲前面3千米,
故选项C正确;
甲到终点的时间不能确定,故选项D说法错误.
故选:D.
二、填空题
7.①③
【分析】利用一般地,形如y=kx+b(k≠0,k、b是常数)的函数,叫做一次函数,进而判断得出答案.
【解答】解:函数①y=3x,②y=2x2+1,③y=x﹣1,④中,是一次函数的是:①③.
故答案为:①③.
8.4
【分析】直接利用一次函数的定义分析得出答案.
【解答】解:∵y=(m+4)x|m|﹣3+1是一次函数,
∴|m|﹣3=1,m+4≠0,
解得:m=4.
故答案为:4.
9.-3 ≠3
【分析】根据形如y=kx(k是常数,k≠0)的函数叫做正比例函数,形如y=kx+b(k≠0,k、b是常数)的函数,叫做一次函数进行分析即可.
【解答】解:由题意得:k+3=0,
解得:k=﹣3;
k﹣3≠0,
解得:k≠3,
故答案为:k=﹣3,k≠3.
10.4
【分析】向上平移2个单位长度后直线的解析式为y=2x﹣m+2,又该直线经过点Q(3,4),将点代入直线即可求出答案.
【解答】解:直线y=2x﹣m的图象向上平移2个单位长度后的解析式为:y=2x﹣m+2,
将点(3,4)代入y=2x﹣m+2,得4=6﹣m+2,
解得:m=4,
故答案为:4.
11.x=2.5
【分析】观察图象找到当y=3时x的值即为本题的答案.
【解答】解:观察函数的图象知:y=kx+b的图象经过点P(2.5,3),
即当x=2.5时y=kx+b=3,
所以关于x的方程kx+b=3的解为x=2.5,
故答案为:x=2.5.
12.
【分析】当y<0时,图象在x轴下方,然后再结合图象可得答案.
【解答】解:∵直线y=kx+b与x轴相交于点A(,0),
∴当y<0时,x<,
故答案为:x.
13.y=x+3
【分析】把点A的坐标代入一次函数解析式,列出关于系数k的方程k+3=4,通过解该方程可以求得k的值.
【解答】解:由题意,得
k+3=4,
解得,k=1,
所以,该一次函数的解析式是:y=x+3,
故答案为y=x+3
14.5
【分析】根据x﹣y=3,x+z=6,可以用含x的代数式表示出y和z,然后根据x≥﹣2y,可以得到x的取值范围,从而可以求得所求式子的最小值.
【解答】解:∵x﹣y=3,x+z=6,
∴y=x﹣3,z=6﹣x,
∴x+y+z=x+x﹣3+6﹣x=x+3,
∵x≥﹣2y,
∴x≥﹣2(x﹣3),
解得,x≥2,
∴当x=2时,x+y+z取得最小值,此时x+y+z=2+3=5,
故答案为:5.
15.x=-6
【分析】根据图象:得到当y=9时,x=﹣6,由此可以求得方程kx+b=9的解.
【解答】解:∵如图,一次关系y=kx+b图象经过点(﹣6,9)
∴当y=9时,x=﹣6,
即方程kx+b=9的解是x=﹣6.
故答案是:x=﹣6.
16.(0,-2)
【分析】利用一次函数图象上点的坐标特征,可求出该直线与y轴的交点坐标.
【解答】解:∵一次函数的解析式为y=2x﹣2.
当x=0时,y=2x﹣2=﹣2,
∴直线与y轴的交点坐标为(0,﹣2),
故答案为(0,﹣2).
17.20
【分析】设乘客所携带行李的重量x(kg)与运费y(元)之间的函数关系式为y=kx+b,由待定系数法求出其解即可.
【解答】解:设乘客所携带行李的重量x(kg)与运费y(元)之间的函数关系式为y=kx+b,由题意,得
,
解得:,
则y=30x﹣600.
当y=0时,
30x﹣600=0,
解得:x=20.
故答案为:20.
18.9
【分析】由表格可知,开始油箱中的油为100L,每行驶1小时,油量减少8L,据此可得y与t的关系式.
【解答】解:由题意可得:y=100﹣8t,
当y=28时,28=100﹣8t
解得:t=9.
故答案为:9.
三、解答题
19.解:(1)由y=(m﹣1)+3是关于x的一次函数,得
,解得m=﹣1,
函数解析式为y=﹣2x+3
(2)将x=1代入解析式得y=1≠2,
故不在函数图象上.
20.解:(1)设y﹣1=k(2x+3),
∴y=2kx+3k+1,
∴y是关于x的一次函数;
(2)把x=,y=0代入得﹣k+3k+1=0,解得k=3,
∴y关于x的函数表达式为y=6x+10.
21.解:(1)∵直线y=kx+2与y轴交于点A,
∴A(0,2),
∵将点A向右平移2个单位,再向上平移1个单位,得到点B.
∴B(2,3);
(2)∵点B关于x轴的对称点为点C,B(2,3),
∴C(2,﹣3),
把B(2,3)代入y=kx+2得,3=2k+2,解得k=,
把C(2,﹣3)代入y=kx+2得,﹣3=2k+2,解得k=﹣,
∴若直线y=kx+2与线段BC有公共点,k的取值范围是﹣≤k≤.
22.解:(1)根据题意得,解得,
即b的值为1;
(2)一次函数解析式为y=x+1,
当y=0时,x+1=0,解得x=﹣;
(3)∵k=>0,
∴y随x的增大而增大,
∵x1<x2,
∴y1<y2.
23.解:(1)设过A,B两点的直线解析式为y=ax+b(a≠0),则根据题意,得,
解得,,
则过A,B两点的直线解析式为y=2x+3;
(2)设P点坐标为(x,0),依题意得x=±3,所以P点坐标分别为P1(3,0),P2(﹣3,0).
==,
=×(3﹣)×3=,
所以,△ABP的面积为或.
24.解:(1)设乙对应的函数关系式为y=kx+b
将点(4,300),(1,0)代入y=kx+b得:
解得:,
∴乙对应的函数关系式y=100x﹣100;
(2)易得甲车对应的函数解析式为y=60x,
联立,
解得:,2.5﹣1=1.5(小时),
∴乙车出发后1.5小时追上甲车.
25.解:(1)设售价为x元,
则平均每月的销售量y(件)与x满足的函数关系式为:y=20+2(80﹣x),
化简整理,得y=﹣2x+180;
故答案是:y=﹣2x+180;
(2)根据题意,得
(x﹣40)(﹣2x+180)=1200,
解得x1=70,x2=60.
因为是尽可能增大销售量,所以x=60符合题意.
答:这款毛衣降价后的售价为60元时,商场当天可获利1200元.
