沪教版八年级数学下册试题 第二十章 一次函数与二元一次方程组(含解析)
文档属性
| 名称 | 沪教版八年级数学下册试题 第二十章 一次函数与二元一次方程组(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-04-17 00:00:00 | ||
图片预览


文档简介
一次函数与二元一次方程组
一、单选题
1.如图所示,一次函数(是常数,)与一次函数(是常数)的图象相交于点,下列判断错误的是( )
A.关于的方程的解是
B.关于的不等式的解集是
C.当时,函数的值比函数的值小
D.关于,的方程组的解是
2.对于实数a,b,我们定义符号max{a,b}的意义为:当a≥b时,max{a,b}=a;当a<b时,max{a,b}=b;如:max{4,﹣2}=4,max{3,3}=3,若关于x的函数为y=max(2x﹣1,﹣x+2},则该函数的最小值是( )
A.2 B.1 C.0 D.﹣1
3.如图,在平面直角坐标系中,点A,B分别在x轴和y轴上,,的角平分线与的垂直平分线交于点C,与交于点D,反比例函数的图象过点C,当面积为1时,k的值为( )
A.1 B.2 C.3 D.4
4.若直线与直线的交点在第一象限,则的取值范围是( ).
A. B. C. D.
5.已知两直线与相交于第四象限,则的取值范围是( )
A. B. C. D.
6.如图,在平面直角坐标系中,点,当四边形 ABCD 的周长最小时,则 m 的值为( ).
A. B. C.2 D.3
7.如图,等腰Rt△ABC中,BC=,以边AC为斜边向右做等腰Rt△ACD,点E是线段CD的中点,连接 AE.作线段CE关于直线AC的对称线段CF,连接BF,并延长BF交线段AE于点G,则线段BG长为( )
A. B. C. D.
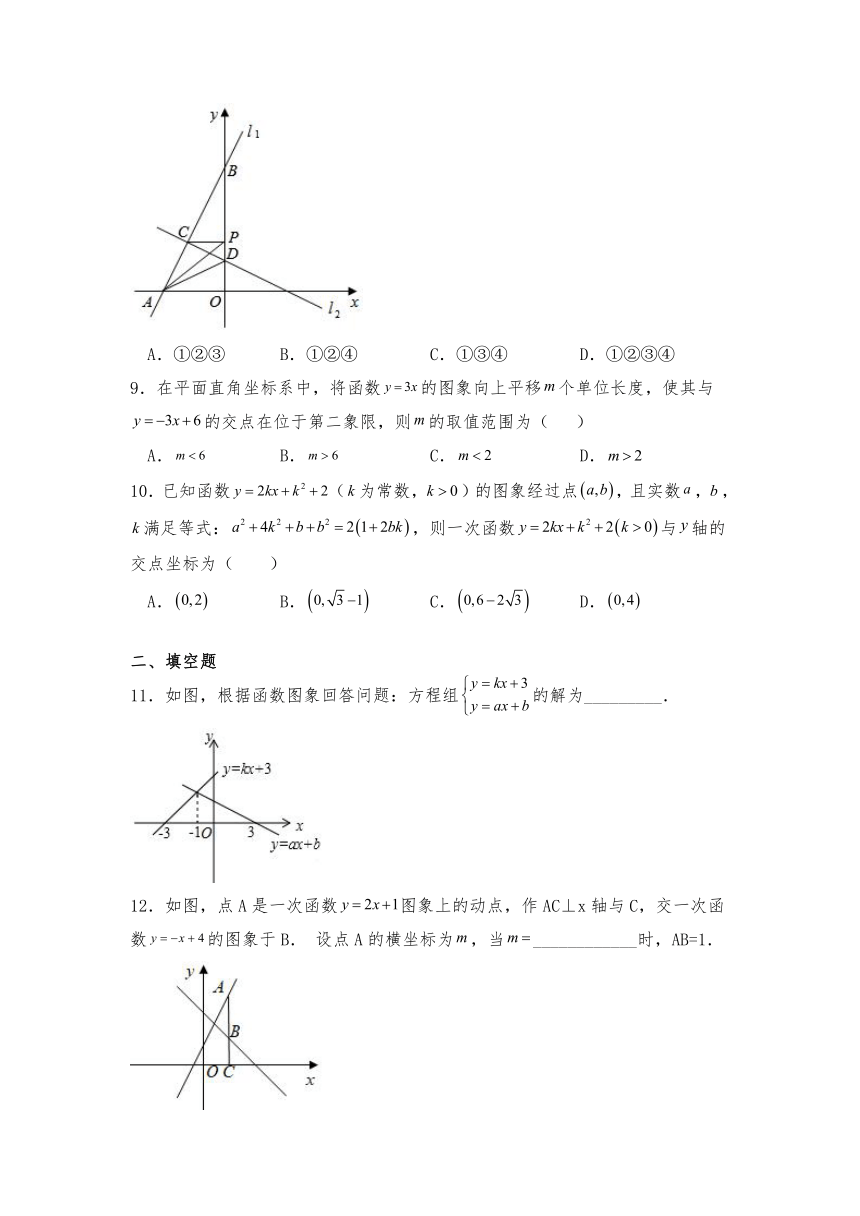
8.已知直线l1:y=kx+b与直线l2:y=﹣x+m都经过C(﹣,),直线l1交y轴于点B(0,4),交x轴于点A,直线l2交y轴于点D,P为y轴上任意一点,连接PA、PC,有以下说法:①方程组的解为;②△BCD为直角三角形;③S△ABD=6;④当PA+PC的值最小时,点P的坐标为(0,1).其中正确的说法是( )
A.①②③ B.①②④ C.①③④ D.①②③④
9.在平面直角坐标系中,将函数的图象向上平移个单位长度,使其与的交点在位于第二象限,则的取值范围为( )
A. B. C. D.
10.已知函数(为常数,)的图象经过点,且实数,,满足等式:,则一次函数与轴的交点坐标为( )
A. B. C. D.
二、填空题
11.如图,根据函数图象回答问题:方程组的解为_________.
12.如图,点A是一次函数图象上的动点,作AC⊥x轴与C,交一次函数的图象于B. 设点A的横坐标为,当____________时,AB=1.
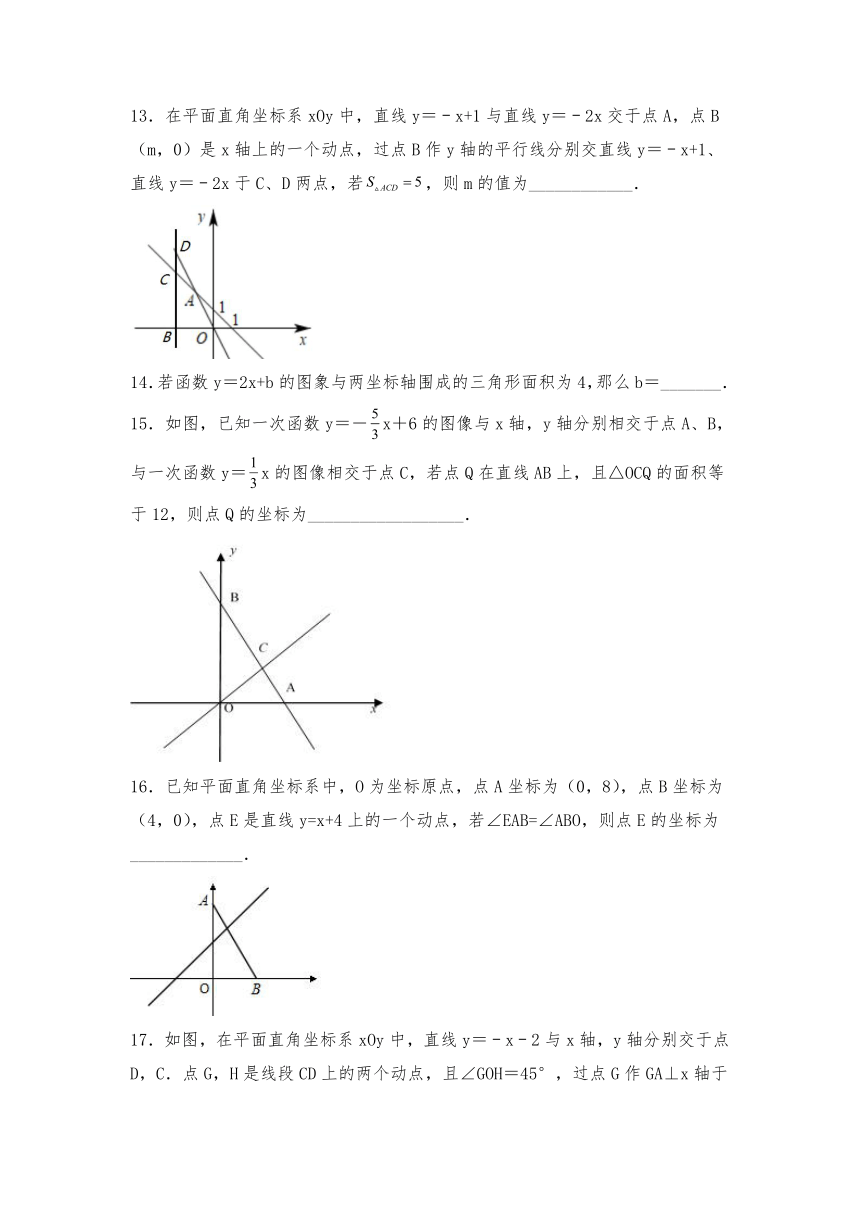
13.在平面直角坐标系xOy中,直线y=﹣x+1与直线y=﹣2x交于点A,点B(m,0)是x轴上的一个动点,过点B作y轴的平行线分别交直线y=﹣x+1、直线y=﹣2x于C、D两点,若,则m的值为____________.
14.若函数y=2x+b的图象与两坐标轴围成的三角形面积为4,那么b=_______.
15.如图,已知一次函数y=-x+6的图像与x轴,y轴分别相交于点A、B,与一次函数y=x的图像相交于点C,若点Q在直线AB上,且△OCQ的面积等于12,则点Q的坐标为__________________.
16.已知平面直角坐标系中,O为坐标原点,点A坐标为(0,8),点B坐标为(4,0),点E是直线y=x+4上的一个动点,若∠EAB=∠ABO,则点E的坐标为_____________.
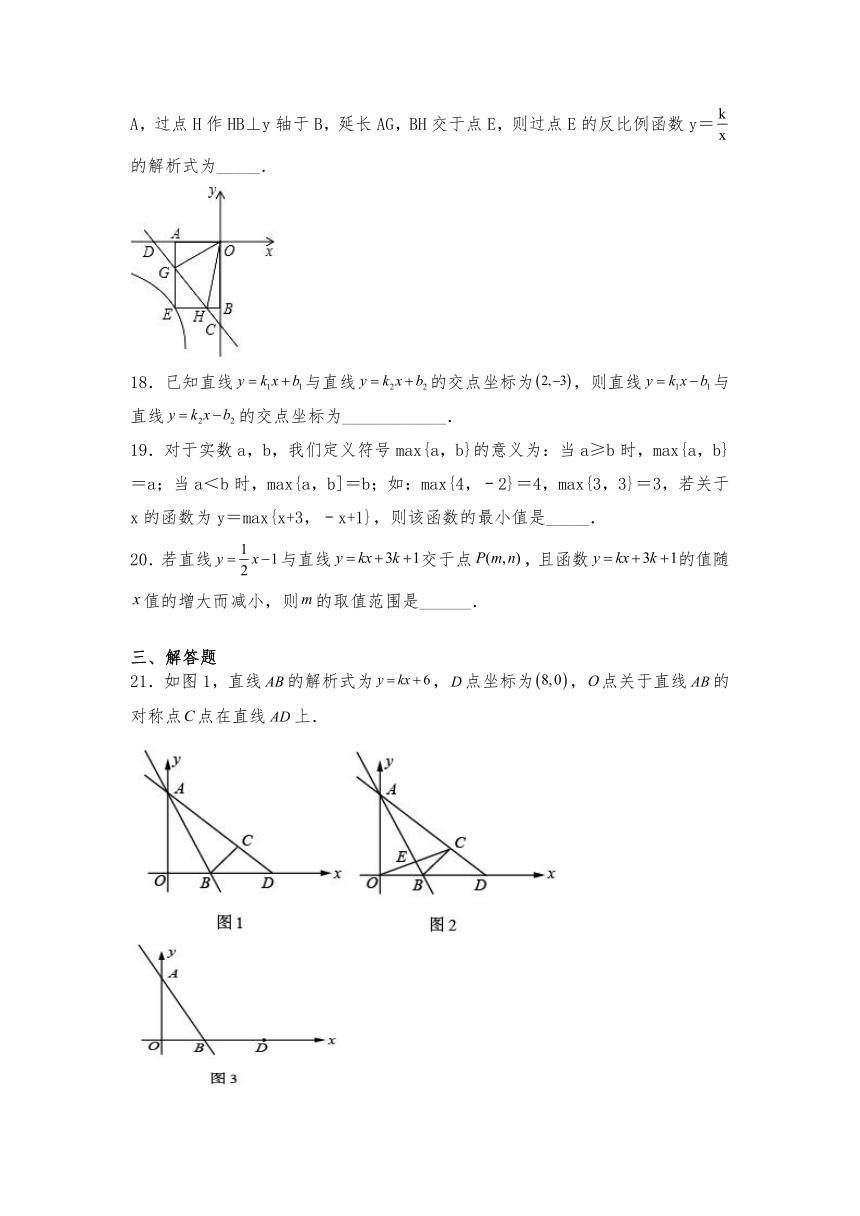
17.如图,在平面直角坐标系xOy中,直线y=﹣x﹣2与x轴,y轴分别交于点D,C.点G,H是线段CD上的两个动点,且∠GOH=45°,过点G作GA⊥x轴于A,过点H作HB⊥y轴于B,延长AG,BH交于点E,则过点E的反比例函数y=的解析式为_____.
18.已知直线与直线的交点坐标为,则直线与直线的交点坐标为____________.
19.对于实数a,b,我们定义符号max{a,b}的意义为:当a≥b时,max{a,b}=a;当a<b时,max{a,b]=b;如:max{4,﹣2}=4,max{3,3}=3,若关于x的函数为y=max{x+3,﹣x+1},则该函数的最小值是_____.
20.若直线与直线交于点,且函数的值随值的增大而减小,则的取值范围是______.
三、解答题
21.如图1,直线的解析式为,点坐标为,点关于直线的对称点点在直线上.
(1)求直线、的解析式;
(2)如图2,若交于点,在线段上是否存在一点,使与的面积相等,若存在求出点坐标,若不存在,请说明理由;
(3)如图3,过点的直线.当它与直线夹角等于时,求出相应的值.
22.定义:图象与x轴有两个交点的函数y=叫做关于m的对称函数,它与x轴负半轴交点记为A,与x轴正半轴交点记为B,
(1)关于l的对称函数y=与直线x=1交于点C,如图.
①直接写出点的坐标:A( ,0);B( ,0);C(1, );
②P为关于l的对称函数图象上一点(点P不与点C重合),当时,求点P的坐标;
(2)当直线y=x与关于m的对称函数有两个交点时,求m的取值范围.
23.如图1,直线与坐标轴分别交于点A、B,与直线交于点C.
(1)求A、C两点的坐标;
(2)如图2,若有一条垂直于x轴的直线l以每秒1个单位的速度从点A出发沿射线方向作匀速滑动,分别交直线、及x轴于点M、N和Q.设运动时间为,连接.
①当时,求t的值.
②若四边形为平行四边形,试求出E点的坐标;
(3)试探究在坐标平面内是否存在点P,使得以O、Q、C、P为顶点的四边形构成菱形?若存在,请直接写出t的值;若不存在,请说明理由.
24.如图,在平面直角坐标系中,点O为坐标原点.△ABO的顶点A在y轴的正半轴上,且OA=16,顶点B在x轴正半轴上,且B(12,0),BE是△ABO的角平分线,且AB=20.
(1)直接写出E点坐标;
(2)点D是射线BO上的一个动点(点D不与点B、点O重合),连接DE,设D点的横坐标为t,△BDE的面积为S,求S与t的关系式,并直接写出t的取值范围;
(3)在(2)的条件下,如图3,当点D在线段OB上,连接AD,AD、BE相交于点F,过点F作FM⊥AD交AB于点M,FN⊥BE交AB于点N,当S=20时,求线段MN的长度.
25.定义:如果一条直线把一个平面图形的面积分成相等的两部分,我们把这条直线称为平面图形的一条面积等分线.
(1)如图1,已知,请用尺规作出的一条面积等分线.
(2)已知:如图2,在平面直角坐标系中,矩形的边在x轴的正半轴上、在y轴的正半轴上,.
①请判断直线是否为矩形的面积等分线,并说明理由;
②若矩形的面积等分线与坐标轴所围成的三角形面积为4,请直接写出此面积等分线的函数表达式.
(3)如图3,在中,点A的坐标为,点B的坐标为,点C的坐标为,点D的坐标,求过点D的一条的面积等分线的解析式.
(4)在中点A的坐标为,点B的坐标为,点C的坐标为,直线是的一条面积等分线,请直接写出b的取值范围.
26.平面直角坐标系中,直线与轴交于点,与轴交于点,直线与轴交于点,与直线交于点.
(1)当时,求点的坐标;
(2)如图1,点为的中点,过点作轴于,交直线于点,若,求的值;
(3)如图2,点在第二象限内,轴于,以为边向左作正方形,的延长线交直线于点,若,求点的坐标.
27.已知:在平面直角坐标系中,直线与直线交于点A.
(1)请证明:无论m为何值,直线,总经过点.
(2)当时,求点A的坐标.
(3)函数的图像与直线、直线围成的封闭区域(不含边界)为W,横纵坐标都为整数的点叫做整点.
①当时,画出函数图像,并直接写出区域W内整点的个数.
②当区域W内恰好有三个整点时,直接写出m的取值范围.
28.如图,在平面直角坐标系中,直线y=﹣0.5x+2与x轴,y轴分别交于点A和点B,与直线y=x交于点C、P(m,0)为x轴上一动点(P不与原点重合),过P作x轴垂线与直线y=x和y=﹣0.5x+2分别交于点M和点N,过N作x轴的平行线交直线y=x于D.
(1)求C点坐标;
(2)求当MN=OB时,m的值;并直接写出此时四边形COPN的面积= ;
(3)直接写出当DN=2NP时,m的值= ;
(4)过D作y轴平行线交直线AB于点E,P点在运动过程中,的值= .
29.如图,在平面直角坐标系中,直线l1的解析式为y=x,直线l2的解析式为y=﹣x+3,与x轴、y轴分别交于点A、点B,直线l1与l2交于点C.
(1)求出点A、点B的坐标;
(2)求△COB的面积;
(3)在y轴上是否存在一点P,使得△PBC为等腰三角形?若存在,请直接写出点P坐标,若不存在,请说明理由.
答案
一、单选题
1.B
【思路指引】
根据条件结合图象对各选项进行判断即可.
【详解详析】
解:∵一次函数(是常数,)与一次函数(是常数)的图象相交于点,
∴关于的方程的解是,选项A判断正确,不符合题意;
∵由图可知,直线在直线上方时,都在点的左侧,
∴关于的不等式的解集是,选项B判断错误,符合题意;
∵当x<0时,直线在直线上方,
∴当x<0时,函数的值比函数的值小,选项C判断正确,不符合题意;
∵一次函数(是常数,)与一次函数(是常数)的图象相交于点,
∴关于,的方程组的解是,选项D判断正确,不符合题意;
故选:B.
2.B
【思路指引】
联立两函数解析式成方程组,通过解方程组找出交点坐标,再根据max{a,b}的意义即可得出函数的最小值.
【详解详析】
解:联立两函数解析式成方程组,得: ,
解得: .
∴当x<1时,y=max(2x﹣1,﹣x+2}=-x+2>1;当x≥1时,y=max(2x﹣1,﹣x+2}=2x-1≥1.
∴函数y=max(2x﹣1,﹣x+2}最小值为1.
故选B.
3.C
【思路指引】
根据 ,得到OB=2OA,设OA=a,则OB=2a,设直线AB的解析式是y=kx+b,利用待定系数法求出直线AB的解析式是y=﹣2x+2a,根据题意可得OD的解析式是y=x,由此求出D的坐标,再根据求解即可.
【详解详析】
解:∵ ,
∴OB=2OA,
设OA=a,则OB=2a,
设直线AB的解析式是y=kx+b,
根据题意得: ,
解得: ,
则直线AB的解析式是y=﹣2x+2a,
∵∠AOB=90°,OC平分∠AOB,
∴∠BOC=∠AOC=45°,
CE=OE=,
∴OD的解析式是y=x,
根据题意得: ,
解得: ,
则D的坐标是(,),
∴CE=OE=,
∴C的坐标是(,),
∴,
∴,
∴,
∴,
故选C.
4.C
【思路指引】
联立两直线解析式求出交点坐标,再根据交点在第一象限列出不等式组求解即可.
【详解详析】
解:根据题意,联立方程组,
解得:,
则两直线交点坐标为,,
两直线交点在第一象限,
,
解得:,
故选:C.
5.A
【思路指引】
先求出交点坐标,然后列不等式组即可求解.
【详解详析】
解:由题意得,
,
解得
,
∵两直线与相交于第四象限,
∴,
∴-6<k<0;
故选:A.
6.B
【思路指引】
首先证明四边形ABCD是平行四边形,再根据垂线段最短解决问题即可.
【详解详析】
解:∵A(1,5),B(4,1),C(m,-m),D(m-3,-m+4),
∴,,
∴AB=CD,
∵点B向左平移3个单位,再向上平移4个单位得到A,点C向左平移3个单位,再向上平移4个单位得到D,
∴AB∥CD,AB=CD,
∴四边形ABCD是平行四边形,
∴BC=CD,
故四边形ABCD的周长为2(AB+BC),而AB=5,故只要BC最短,则周长最短,
∵C点的横坐标与纵坐标互为相反数,
∴点C在直线y=-x上运动,
∴由点到直线的距离垂线段最短可知, BC⊥直线y=-x 时,BC的值最小,如下图所示:
易求得直线BC的解析式为:y=x-3
C点所在的直线为:y=-x,联立两个一次函数解析式:
,解得,故,
故选:B.
7.B
【思路指引】
建立如下图所示坐标系,使BC与x轴重合,AC与y轴重合,可将各点坐标求出,并通过两点式分别求出直线BF、直线AE的解析式,直线BF与AE相交于点G,即可求出BG的长度.
【详解详析】
解:建立如图所示坐标系,使BC与x轴重合,AC与y轴重合,
∵ABC和ACD都是等腰直角三角形,且BC=,
∴AC=BC=,AB=,AD=CD=,
可将各点坐标表示出来,A(0,),B(,0),C(0,0),D(,),
∴点E为CD中点,故E的坐标为(,),
又∵CF为CE关于AC的对称线段,故F的坐标为(,),
设直线BF的解析式为:y=kx+b,将B点、F点坐标代入,
,解得:,
∴直线BF的解析式为:,
设直线AE的解析式为:y=mx+n,将A点、E点坐标代入,
,解得:,
∴直线BF的解析式为:,
直线BF与AE相交于点G,
,解得:,即G(,),
线段BG的长度为:,
故选:B.
8.B
【思路指引】
根据一次函数图象与二元一次方程的关系,利用交点坐标可得方程组的解;根据两直线的系数的积为-1,可知两直线互相垂直;求得BD和AO的长,根据三角形面积计算公式,即可得到△ABD的面积;根据轴对称的性质以及两点之间,线段最短,即可得到当PA+PC的值最小时,点P的坐标为(0,1).
【详解详析】
解:①∵直线l1:y=kx+b与直线l2:y=﹣x+m都经过C(﹣,),
∴方程组的解为,
故①正确,符合题意;
②把B(0,4),C(﹣,)代入直线l1:y=kx+b,可得,解得,
∴直线l1:y=2x+4,
又∵直线l2:y=﹣x+m,
∴直线l1与直线l2互相垂直,即∠BCD=90°,
∴△BCD为直角三角形,
故②正确,符合题意;
③把C(﹣,)代入直线l2:y=﹣x+m,可得m=1,
y=﹣x+1中,令x=0,则y=1,
∴D(0,1),
∴BD=4﹣1=3,
在直线l1:y=2x+4中,令y=0,则x=﹣2,
∴A(﹣2,0),
∴AO=2,
∴S△ABD=×3×2=3,
故③错误,不符合题意
④点A关于y轴对称的点为A'(2,0),
由点C、A′的坐标得,直线CA′的表达式为:y=﹣x+1,
令x=0,则y=1,
∴当PA+PC的值最小时,点P的坐标为(0,1),
故④正确,符合题意;
故选:B.
9.B
【思路指引】
先求出平移后的函数解析式,再联立它与另一个函数解析式求出它们的交点坐标,根据第二象限的坐标特点为,得到关于m的不等式组,解这个不等式组即可得出m的取值范围.
【详解详析】
解:将函数的图像向上平移m个单位长度后的图像的解析式为,
联立后可以得到:,
解得,
因为它们的交点在第二象限,
即,
解得,
,
故选:B.
10.C
【思路指引】
将点代入函数中,得到关于,,的关系式,将看作常数,再联立满足的等式组成二元一次方程组,将,用含的式子表示出来,此时再回代入函数中,求解出的值,最后在一次函数中令,求解出y的值,最终表示出交点坐标即可.
【详解详析】
解:将点代入函数中,
得:,
又∵,
化简可得:
此时联立方程组可得: ,
解得:,
∴点的坐标可表示为(-k,2k),
将(-k,2k)代入得:
,
解得,
∵为常数且,
∴,
此时一次函数,
令,
解得:,
∴交点坐标为.
故选:C.
二、填空题
11.
【思路指引】
首先观察函数的图象y=kx+3经过点(-3,0),然后求得k值确定函数的解析式,最后求得两图象的交点求方程组的解即可;
【详解详析】
解:根据图象知:y=kx+3经过点(-3,0),
所以-3k+3=0, 解得:k=1,
所以解析式为y=x+3,
当x=-1时,y=2,
所以两个函数图象均经过(-1,2),
所以方程组 的解为,
故答案为:.
12.或
【思路指引】
分别用m表示出点A和点B的纵坐标,用点A的纵坐标减去点B的纵坐标或用点B的纵坐标减去点A的纵坐标得到以m为未知数的方程,求解即可.
【详解详析】
解:∵点A是一次函数图象上的动点,且点A的横坐标为,
∴
∵AC⊥x轴与C,
∴
∴
∵
∴
解得,或
故答案为或
13.或
【思路指引】
分别求出A、C、D三点坐标,根据,利用坐标列式计算即可.
【详解详析】
∵由直线y=﹣x+1与直线y=﹣2x交于点A,
∴点A坐标(-1,2),
∵过点B(m,0)作y轴的平行线分别交直线y=﹣x+1、直线y=﹣2x于C、D两点,
∴点C坐标(m,1-m),点D坐标(m,-2m).
∴,
解得
故答案为或.
14.±4
【思路指引】
利用一次函数y=2x+b的图象与x轴交点和与y轴交点的特点求出坐标,以及图象与坐标轴所围成的三角形是直角三角形求解.
【详解详析】
解:∵当y=0时,0=2x+b,
∴;
当x=0时,y=b,
∴一次函数y=2x+b的图象与坐标轴所围成的三角形面积:,
解得,
故答案为:.
15.(-1,)(7,-)
【思路指引】
根据题意联立两个一次函数可确定点C的坐标,然后确定点A、点B的坐标,分两种情况讨论:①当点Q位于线段BC上时,设,求得,由此可得点Q必在点B左侧,即,可得,代入求解即可得点Q的坐标;②当点Q位于C点右侧时,设,根据图形可得,代入求解即可得点Q的坐标.
【详解详析】
解:根据题意分两种情况进行讨论,
,
解得:,
∴,
令代入得:,
令代入得:,
①当点Q位于线段BC上时,如图即点Q的位置,设,
,
∴点Q必在点B左侧,即,
,
,
,
解得:,
∴,
则,
∴;
②当点Q位于C点右侧时,如图即点Q的位置,设,
,
,
,
解得:,
则,
∴;
综上可得:或,
故答案为:或.
16.(-12,-8);(4,8)
【思路指引】
分两种情况:当点E在y轴右侧时,由条件可判定AE∥BO,容易求得E点坐标;当点E在y轴左侧时,可设E点坐标为(a,a+4),过AE作直线交x轴于点C,可表示出直线AE的解析式,可表示出C点坐标,再根据勾股定理可表示出AC的长,由条件可得到AC=BC,可得到关于a的方程,可求得E点坐标.
【详解详析】
(1)当点E在y轴右侧时,如图1,连接AE,
∵∠EAB=∠ABO,
∴AE∥OB,
∵A(0,8),
∴E点纵坐标为8,
又E点在直线y=x+4上,把y=8代入可求得x=4,
∴E点坐标为(4,8);
(2)当点E在y轴左侧时,过A、E作直线交x轴于点C,如图2,
设C(m,0),
∵∠EAB=∠ABO,
∴AC=BC,
∴(4-m)2=m2+82,
解得m=-6,
∴C(6,0)
∴直线AC的解析式为,
∵E是直线AC与y=x+4的交点
∴联立,解得
∴E(-12,-8).
综上可知,E点坐标为(4,8)或(-12,-8).
故答案为:(4,8)或(-12,-8).
17.y=
【思路指引】
过点G作GP⊥GO,交OH的延长线于点P,过点P作PN⊥AE,交AE延长线于N,设点A(-,0)则AO=,DO=2,AD=2-,由“AAS”可证△GAO≌△PNG,可得NP=AG=2-,AO=GN=,可求点P坐标,求出一次函数解析式,可求点H的纵坐标,即可求解.
【详解详析】
解:如图,过点G作GP⊥GO,交OH的延长线于点P,过点P作PN⊥AE,交AE延长线于N,
设点A(-,0)
∴AO=,
∵直线y=﹣x﹣2与x轴,y轴分别交于点D,C,
∴点D(﹣2,0),∠ADC=45°,
∴DO=2,AD=2﹣,
∵AE⊥OD,
∴∠ADG=∠AGD=45°,
∴AD=AG=2﹣,
∵GP⊥GO,∠GOH=45°,
∴∠GPO=∠GOP=45°,
∴GP=GO,
∵∠AGO+∠AOG=90°,∠AGO+∠NGP=90°,
∴∠AOG=∠NGP,
又∵∠GNP=∠GAO=90°,GO=GP,
∴△GAO≌△PNG(AAS),
∴NP=AG=2﹣,AO=GN=,
∴AN=2,
∴点P(2﹣2,﹣2),
∴直线OP解析式为:y= x,
联立方程组
∴
∴点H的纵坐标为,
∴点E(,)
∵反比例函数y=的图象过点E,
∴k=×()=2,
∴反比例函数解析式为:y=,
故答案为:y= .
18.(-2,3).
【思路指引】
由,得到,根据直线与直线的交点坐标为,得到,进而得到,将代入中,即可求解.
【详解详析】
解:∵
∴
∵直线与直线的交点坐标为
∴
得
∴
∴
将代入中得
∴交点坐标为(-2,3)
故答案为:(-2,3).
19.2
【思路指引】
联立两函数解析式成方程组,通过解方程组找出交点坐标,再根据max{a,b}的意义即可得出函数的最小值.
【详解详析】
解:联立两函数解析式成方程组,得:,
解得:.
∴当x<﹣1时,y=max{x+3,﹣x+1}=﹣x+1>2;当x≥﹣1时,y=max{x+3,﹣x+1}=x+3≥2.
∴函数y=max{x+3,﹣x+1}最小值为2.
故答案为:2.
20.
【思路指引】
根据一次函数与二元一次方程组的关系可得,求得,再由一次函数的性质可得,则可得出关于m的一元一次不等式组,求解后即可得出结果.
【详解详析】
解:∵直线与直线交于点,
∴ ,
∴,
∴,
∵函数的值随值的增大而减小,
∴,
即,
∴或,
当时,,,此不等式组无解;
当时,,,不等式组的解集为.
∴的取值范围是.
故答案为:.
三、解答题
21.
解:(1),
,即,
又,
,
设直线的解析式为,将点代入得,
直线的解析式为.
在中,,
点、点关于直线对称,
设,,,
,
在中,,
(面积法亦可)
,
直线的解析式为.
(2)由(1)得,BC=OB=3,CD=4,BD=5,
则,
解得:,
将代入中,求得:
则,直线的解析式为:,
直线的解析式为:.
,
,
,
设直线的解析式为:,
在直线上,
,
,
直线的解析式为:,
联立得:,解得:.
故存在,.
(3)如图,设若直线、与直线夹角等于,
即为等腰直角三角形,作于,于,
则,
,,
直线过,
即,解得:,
直线的解析式为:,
设坐标为,则,,
点坐标为,
点在直线上,
,
解得:,
,.
当直线过点时,,解得:,
当直线过点时,,解得:.
所以或.
22.
解:(1)①当时,令,即,解得,此时满足题意,故.
当时,令,即,解得,此时满足题意,故.
当时,,故.
故答案为:,2,2.
②∵,,,
∴AB=4,.
∴.
∵,
∴.
∴.
∴或.
当,且时,令,即,解得,此时与点C重合,故舍去.
当,且时,令,即,解得,此时符合题意,故.
当,且时,令,即,解得,此时符合题意,故.
当,且时,令,即,解得,此时符合题意,故.
故点P坐标为或或.
(2)∵关于m的对称函数的解析式为
∴该函数图象为两个一次函数图象的一部分结合起来的图象.
∵一次函数图象与x轴最多只有一个交点,且关于m的对称函数与x轴有两个交点,
∴组成该对称函数的两个一次函数图象的部分图象都与x轴有交点.
∵对于,令y=0,即,解得x=2,
∴x=2必须在的范围之内.
∴.
∵对于,令y=0,即,解得,
∴必须在的范围之内.
∴.
∴.
∵直线y=x与关于m的对称函数有两个交点,
∴直线y=x分别与直线和各有一个交点.
对于直线y=x与直线,
联立可得解得
∴直线y=x与直线必有一交点.
对于直线y=x与直线,
联立可得解得
∵,
∴必须在的范围之内才能保证直线y=x与直线有交点.
∴.
∴.
∴m的取值范围是.
23.
解:(1)对于直线,令x=0得到y=3,令y=0,得到x=6,
∴A(6,0),B(0,3).
联立,
解得,
∴C(2,2),
(2)①设M(6-t,-(6-t)+3),N(6-t,6-t),
∴MN=|-(6-t)+3-(6-t)|=|t-6|,
∵OA=2MN,
∴6=2|t-6|,
解得t=2或6;
②∵四边形CMEN是平行四边形
∴CM∥EN,CN∥ME,
∴,,
设直线ME的解析式为,直线EN的解析式为
把M(6-t,-(6-t)+3)代入中,
∴,
把N(6-t,6-t)代入中,
∴
∴直线ME的解析式为,直线EN的解析式为
解得:
∴E的坐标为(,);
(3)∵C(2,2),
∴
当OC为菱形的边时,可得(,0),(,0),(,0),
当OC为菱形的对角线时,可得(2,0),
∴或或或时以O、Q、C、P为顶点的四边形构成菱形.
24.
(1)过点作于点,如图1,
BE是△ABO的角平分线,
设点
则,
解得
(2)如图2,
点D是射线BO上的一个动点,点D不与点B、点O重合,D点的横坐标为t,
且
,
当,,
,,
(且),
;
(3)如图3,当点D在线段OB上,
,
解得,
,
,
,
设的解析式为,
则,
解得,
,
设的解析式为,
,
,
解得,
,
交点为,
,
解得,
,
过点作于点,过点作于点,连接,
则,
BE是△ABO的角平分线,,
,
,
,
,
,
,
,
设,
,
,
,
,
,
,
即,
,
整理得:,
即,
解得,
.
25.解:(1)如图1所示,作出BC的垂直平分线交BC于点D,连接AD,
∴AD是三角形ABC的中线,
∴AC所在直线即要求的的一条面积等分线.
(2)①如图2所示,连接AC,OB交于点M.
∵OA=6,OC=4,
∴,,
∴,
∵四边形OABC是矩形,
∴矩形OABC的面积等分线必过点M,
将x=3代入中,得:
,
∴直线不过点M,
∴直线不是矩形OABC的面积等分线;
②如图所示,
由①知,矩形OABC的面积等分线必过点M(3,2),
设矩形OABC的面积等分线的解析式为y=kx+b与x轴相交于点E,与y轴相交于F,
∴3k+b=2,
∴b=2 3k,
∴矩形OABC的面积等分线的解析式为y=kx+2 3k,
令x=0,y=2 3k,
∴F(0,2 3k),
∴OF=|2 3k|,
令y=0,
∴x=,
∴E(,0),
∴OE=,
∵矩形OABC的面积等分线与坐标轴所围成的三角形面积为4,
∴,
∴OE OF=8,
∴|2 3k| ||=8,
∴k=2或k=,
∴矩形OABC的面积等分线函数表达式为y=2x 4或y=x+.
(3)如图所示,设三角形ABC面积的等分线的表达式为,交x轴于点F,交AB于点E.
∵三角形ABC面积的等分线过点D,
∴将D代入表达式得:b=-2,
∴表达式为.
将y=0代入得:x=,
∴F.
∴AF=.
∵点A的坐标为,点B的坐标为,
利用待定系数法可得AB的表达式为,
∵DE和AB交于点E,
∴联立表达式得:,
解得:.
∵,
∴,
∴,
代入得:,
整理得:,
解得:(舍去),
∴三角形ABC面积的等分线的表达式为.
(4)如图所示,
∵直线是的一条面积等分线,
由图像可知,
当或时,无论a取何值,直线都不能把的面积平分,
∴.
26.解:(1)当k=1时,直线l2为y=x+2.
解方程组,
解得,
∴P;
(2)当y=0时,kx+2k=0,
∵k≠0,
∴x=-2
∴C(-2,0),OC=2
当y=0时,,
∴x=6,
∴A(6,0),OA=6
过点P作PG⊥DF于点G,
∵,
∴PG∥x轴,
∴∠GPD=∠EAD,∠PGD=∠AED=90°,
∵点为的中点,
∴PD=AD,
在△PDG和△ADE中
,
∴△PDG≌△ADE(AAS),
∴DG = DE,
∵,
∴FG+GD=DF=2DE,
∴FG=GD,
∵PG⊥DF,
∴PD=PF,
∴∠PFD=∠PDF,
∵∠PFD+∠PCA=90°,∠PDF+∠PAC=90°,
∴∠PCA=∠PAC,
∴PC=PA,
过点P作PH⊥CA于点H,
∴CH=CA=4,
∴OH=CH-OC=4-2=2,
当x=2时,,
∴点P(2,2),
把点P代入y=kx+2k,得2k+2k=2,
∴;
(3)∵以为边向左作正方形,
∴PQ=PM,∠RQP=∠CMP=90°
在Rt△PMC和Rt△PQR中
∴Rt△PMC≌Rt△PQR(HL),
∴CM=RQ,
∴NR=NC,
设NR=NC=a,
则R(-a-2,a),
代入,得,
解得,a=8,
设P(m,n),
则,
∵ON=a+2=8+2=10,
∴NM=ON-OM=10+m,
∵PM=NM,
即10+m=,
解得m=,,
∴P.
27.(1)证明:当m=0时,直线为y=x,当x=2时y=2,此时直线经过点(2,2);
当m=1时,直线为y=2x-2,当x=2时y=2,此时直线经过点(2,2);
当m=2时,直线为y=3x-4,当x=2时y=2,此时直线经过点(2,2);
当x=2时,,
∴无论m为何值,直线,总经过点.
(2)解:当时,直线为,
∵直线与直线交于点A,
∴当时,y=3,
∴A(4,3);
(3)①如图,当x=1时,区域内函数值最小为1,最大为;
当x=2时,区域内函数值最小为,最大为2,存在整点(2,1);
当x=3时,区域内函数值最小为,最大为,存在整点(3,1)、(3,2);
故整点有(2,1)、(3,1)、(3,2)共3个;
②当区域W内恰好有三个整点时,即(2,1)、(3,1)、(3,2),且无论m为何值,直线总经过点,
∴当x=3时,,
∴.
28.解:(1)联立两直线解析式,可得
解得,即点坐标为
故答案为
(2)设,则,
线段
由题意可得:,,则
∴,解得或(舍去)
四边形COPN的面积
故答案为,
(3)设,则,
则的纵坐标为
又∵在直线上,
∴的横坐标为
即
,
由题意可得:
化简可得:或
解得或
故答案为或;
(4)由(3)得,则的横坐标为
则的纵坐标为,即
则
由(1)得
∴
故答案为
29.解:(1)∵A、B是直线与x轴,y轴的交点,
∴A点坐标为(6,0),B点坐标为(0,3);
(2)联立,
解得,
∴C点坐标为(2,2),
∵B点坐标为(0,3),
∴OB=3,
∴;
(3)假设存在点P使得△PBC是等腰三角形,
∵B(0,3),C(2,2),
∴,
设P点坐标为(0,m),则,
当PB=BC时,则,
∴,
解得,
∴此时P点坐标为或;
当PC=BC时,过点C作CD⊥BP于D,
∴D点坐标为(0,2),PD=BD,
∴PD=BD=1,
∴BP=2
∴OP=OB-BP=1,
∴P点坐标为(0,1)
当PB=PC时,
∴,
解得,
∴P点坐标为;
∴综上所述,当P点坐标为或或(0,1)或时,使得△PBC为等腰三角形.
一、单选题
1.如图所示,一次函数(是常数,)与一次函数(是常数)的图象相交于点,下列判断错误的是( )
A.关于的方程的解是
B.关于的不等式的解集是
C.当时,函数的值比函数的值小
D.关于,的方程组的解是
2.对于实数a,b,我们定义符号max{a,b}的意义为:当a≥b时,max{a,b}=a;当a<b时,max{a,b}=b;如:max{4,﹣2}=4,max{3,3}=3,若关于x的函数为y=max(2x﹣1,﹣x+2},则该函数的最小值是( )
A.2 B.1 C.0 D.﹣1
3.如图,在平面直角坐标系中,点A,B分别在x轴和y轴上,,的角平分线与的垂直平分线交于点C,与交于点D,反比例函数的图象过点C,当面积为1时,k的值为( )
A.1 B.2 C.3 D.4
4.若直线与直线的交点在第一象限,则的取值范围是( ).
A. B. C. D.
5.已知两直线与相交于第四象限,则的取值范围是( )
A. B. C. D.
6.如图,在平面直角坐标系中,点,当四边形 ABCD 的周长最小时,则 m 的值为( ).
A. B. C.2 D.3
7.如图,等腰Rt△ABC中,BC=,以边AC为斜边向右做等腰Rt△ACD,点E是线段CD的中点,连接 AE.作线段CE关于直线AC的对称线段CF,连接BF,并延长BF交线段AE于点G,则线段BG长为( )
A. B. C. D.
8.已知直线l1:y=kx+b与直线l2:y=﹣x+m都经过C(﹣,),直线l1交y轴于点B(0,4),交x轴于点A,直线l2交y轴于点D,P为y轴上任意一点,连接PA、PC,有以下说法:①方程组的解为;②△BCD为直角三角形;③S△ABD=6;④当PA+PC的值最小时,点P的坐标为(0,1).其中正确的说法是( )
A.①②③ B.①②④ C.①③④ D.①②③④
9.在平面直角坐标系中,将函数的图象向上平移个单位长度,使其与的交点在位于第二象限,则的取值范围为( )
A. B. C. D.
10.已知函数(为常数,)的图象经过点,且实数,,满足等式:,则一次函数与轴的交点坐标为( )
A. B. C. D.
二、填空题
11.如图,根据函数图象回答问题:方程组的解为_________.
12.如图,点A是一次函数图象上的动点,作AC⊥x轴与C,交一次函数的图象于B. 设点A的横坐标为,当____________时,AB=1.
13.在平面直角坐标系xOy中,直线y=﹣x+1与直线y=﹣2x交于点A,点B(m,0)是x轴上的一个动点,过点B作y轴的平行线分别交直线y=﹣x+1、直线y=﹣2x于C、D两点,若,则m的值为____________.
14.若函数y=2x+b的图象与两坐标轴围成的三角形面积为4,那么b=_______.
15.如图,已知一次函数y=-x+6的图像与x轴,y轴分别相交于点A、B,与一次函数y=x的图像相交于点C,若点Q在直线AB上,且△OCQ的面积等于12,则点Q的坐标为__________________.
16.已知平面直角坐标系中,O为坐标原点,点A坐标为(0,8),点B坐标为(4,0),点E是直线y=x+4上的一个动点,若∠EAB=∠ABO,则点E的坐标为_____________.
17.如图,在平面直角坐标系xOy中,直线y=﹣x﹣2与x轴,y轴分别交于点D,C.点G,H是线段CD上的两个动点,且∠GOH=45°,过点G作GA⊥x轴于A,过点H作HB⊥y轴于B,延长AG,BH交于点E,则过点E的反比例函数y=的解析式为_____.
18.已知直线与直线的交点坐标为,则直线与直线的交点坐标为____________.
19.对于实数a,b,我们定义符号max{a,b}的意义为:当a≥b时,max{a,b}=a;当a<b时,max{a,b]=b;如:max{4,﹣2}=4,max{3,3}=3,若关于x的函数为y=max{x+3,﹣x+1},则该函数的最小值是_____.
20.若直线与直线交于点,且函数的值随值的增大而减小,则的取值范围是______.
三、解答题
21.如图1,直线的解析式为,点坐标为,点关于直线的对称点点在直线上.
(1)求直线、的解析式;
(2)如图2,若交于点,在线段上是否存在一点,使与的面积相等,若存在求出点坐标,若不存在,请说明理由;
(3)如图3,过点的直线.当它与直线夹角等于时,求出相应的值.
22.定义:图象与x轴有两个交点的函数y=叫做关于m的对称函数,它与x轴负半轴交点记为A,与x轴正半轴交点记为B,
(1)关于l的对称函数y=与直线x=1交于点C,如图.
①直接写出点的坐标:A( ,0);B( ,0);C(1, );
②P为关于l的对称函数图象上一点(点P不与点C重合),当时,求点P的坐标;
(2)当直线y=x与关于m的对称函数有两个交点时,求m的取值范围.
23.如图1,直线与坐标轴分别交于点A、B,与直线交于点C.
(1)求A、C两点的坐标;
(2)如图2,若有一条垂直于x轴的直线l以每秒1个单位的速度从点A出发沿射线方向作匀速滑动,分别交直线、及x轴于点M、N和Q.设运动时间为,连接.
①当时,求t的值.
②若四边形为平行四边形,试求出E点的坐标;
(3)试探究在坐标平面内是否存在点P,使得以O、Q、C、P为顶点的四边形构成菱形?若存在,请直接写出t的值;若不存在,请说明理由.
24.如图,在平面直角坐标系中,点O为坐标原点.△ABO的顶点A在y轴的正半轴上,且OA=16,顶点B在x轴正半轴上,且B(12,0),BE是△ABO的角平分线,且AB=20.
(1)直接写出E点坐标;
(2)点D是射线BO上的一个动点(点D不与点B、点O重合),连接DE,设D点的横坐标为t,△BDE的面积为S,求S与t的关系式,并直接写出t的取值范围;
(3)在(2)的条件下,如图3,当点D在线段OB上,连接AD,AD、BE相交于点F,过点F作FM⊥AD交AB于点M,FN⊥BE交AB于点N,当S=20时,求线段MN的长度.
25.定义:如果一条直线把一个平面图形的面积分成相等的两部分,我们把这条直线称为平面图形的一条面积等分线.
(1)如图1,已知,请用尺规作出的一条面积等分线.
(2)已知:如图2,在平面直角坐标系中,矩形的边在x轴的正半轴上、在y轴的正半轴上,.
①请判断直线是否为矩形的面积等分线,并说明理由;
②若矩形的面积等分线与坐标轴所围成的三角形面积为4,请直接写出此面积等分线的函数表达式.
(3)如图3,在中,点A的坐标为,点B的坐标为,点C的坐标为,点D的坐标,求过点D的一条的面积等分线的解析式.
(4)在中点A的坐标为,点B的坐标为,点C的坐标为,直线是的一条面积等分线,请直接写出b的取值范围.
26.平面直角坐标系中,直线与轴交于点,与轴交于点,直线与轴交于点,与直线交于点.
(1)当时,求点的坐标;
(2)如图1,点为的中点,过点作轴于,交直线于点,若,求的值;
(3)如图2,点在第二象限内,轴于,以为边向左作正方形,的延长线交直线于点,若,求点的坐标.
27.已知:在平面直角坐标系中,直线与直线交于点A.
(1)请证明:无论m为何值,直线,总经过点.
(2)当时,求点A的坐标.
(3)函数的图像与直线、直线围成的封闭区域(不含边界)为W,横纵坐标都为整数的点叫做整点.
①当时,画出函数图像,并直接写出区域W内整点的个数.
②当区域W内恰好有三个整点时,直接写出m的取值范围.
28.如图,在平面直角坐标系中,直线y=﹣0.5x+2与x轴,y轴分别交于点A和点B,与直线y=x交于点C、P(m,0)为x轴上一动点(P不与原点重合),过P作x轴垂线与直线y=x和y=﹣0.5x+2分别交于点M和点N,过N作x轴的平行线交直线y=x于D.
(1)求C点坐标;
(2)求当MN=OB时,m的值;并直接写出此时四边形COPN的面积= ;
(3)直接写出当DN=2NP时,m的值= ;
(4)过D作y轴平行线交直线AB于点E,P点在运动过程中,的值= .
29.如图,在平面直角坐标系中,直线l1的解析式为y=x,直线l2的解析式为y=﹣x+3,与x轴、y轴分别交于点A、点B,直线l1与l2交于点C.
(1)求出点A、点B的坐标;
(2)求△COB的面积;
(3)在y轴上是否存在一点P,使得△PBC为等腰三角形?若存在,请直接写出点P坐标,若不存在,请说明理由.
答案
一、单选题
1.B
【思路指引】
根据条件结合图象对各选项进行判断即可.
【详解详析】
解:∵一次函数(是常数,)与一次函数(是常数)的图象相交于点,
∴关于的方程的解是,选项A判断正确,不符合题意;
∵由图可知,直线在直线上方时,都在点的左侧,
∴关于的不等式的解集是,选项B判断错误,符合题意;
∵当x<0时,直线在直线上方,
∴当x<0时,函数的值比函数的值小,选项C判断正确,不符合题意;
∵一次函数(是常数,)与一次函数(是常数)的图象相交于点,
∴关于,的方程组的解是,选项D判断正确,不符合题意;
故选:B.
2.B
【思路指引】
联立两函数解析式成方程组,通过解方程组找出交点坐标,再根据max{a,b}的意义即可得出函数的最小值.
【详解详析】
解:联立两函数解析式成方程组,得: ,
解得: .
∴当x<1时,y=max(2x﹣1,﹣x+2}=-x+2>1;当x≥1时,y=max(2x﹣1,﹣x+2}=2x-1≥1.
∴函数y=max(2x﹣1,﹣x+2}最小值为1.
故选B.
3.C
【思路指引】
根据 ,得到OB=2OA,设OA=a,则OB=2a,设直线AB的解析式是y=kx+b,利用待定系数法求出直线AB的解析式是y=﹣2x+2a,根据题意可得OD的解析式是y=x,由此求出D的坐标,再根据求解即可.
【详解详析】
解:∵ ,
∴OB=2OA,
设OA=a,则OB=2a,
设直线AB的解析式是y=kx+b,
根据题意得: ,
解得: ,
则直线AB的解析式是y=﹣2x+2a,
∵∠AOB=90°,OC平分∠AOB,
∴∠BOC=∠AOC=45°,
CE=OE=,
∴OD的解析式是y=x,
根据题意得: ,
解得: ,
则D的坐标是(,),
∴CE=OE=,
∴C的坐标是(,),
∴,
∴,
∴,
∴,
故选C.
4.C
【思路指引】
联立两直线解析式求出交点坐标,再根据交点在第一象限列出不等式组求解即可.
【详解详析】
解:根据题意,联立方程组,
解得:,
则两直线交点坐标为,,
两直线交点在第一象限,
,
解得:,
故选:C.
5.A
【思路指引】
先求出交点坐标,然后列不等式组即可求解.
【详解详析】
解:由题意得,
,
解得
,
∵两直线与相交于第四象限,
∴,
∴-6<k<0;
故选:A.
6.B
【思路指引】
首先证明四边形ABCD是平行四边形,再根据垂线段最短解决问题即可.
【详解详析】
解:∵A(1,5),B(4,1),C(m,-m),D(m-3,-m+4),
∴,,
∴AB=CD,
∵点B向左平移3个单位,再向上平移4个单位得到A,点C向左平移3个单位,再向上平移4个单位得到D,
∴AB∥CD,AB=CD,
∴四边形ABCD是平行四边形,
∴BC=CD,
故四边形ABCD的周长为2(AB+BC),而AB=5,故只要BC最短,则周长最短,
∵C点的横坐标与纵坐标互为相反数,
∴点C在直线y=-x上运动,
∴由点到直线的距离垂线段最短可知, BC⊥直线y=-x 时,BC的值最小,如下图所示:
易求得直线BC的解析式为:y=x-3
C点所在的直线为:y=-x,联立两个一次函数解析式:
,解得,故,
故选:B.
7.B
【思路指引】
建立如下图所示坐标系,使BC与x轴重合,AC与y轴重合,可将各点坐标求出,并通过两点式分别求出直线BF、直线AE的解析式,直线BF与AE相交于点G,即可求出BG的长度.
【详解详析】
解:建立如图所示坐标系,使BC与x轴重合,AC与y轴重合,
∵ABC和ACD都是等腰直角三角形,且BC=,
∴AC=BC=,AB=,AD=CD=,
可将各点坐标表示出来,A(0,),B(,0),C(0,0),D(,),
∴点E为CD中点,故E的坐标为(,),
又∵CF为CE关于AC的对称线段,故F的坐标为(,),
设直线BF的解析式为:y=kx+b,将B点、F点坐标代入,
,解得:,
∴直线BF的解析式为:,
设直线AE的解析式为:y=mx+n,将A点、E点坐标代入,
,解得:,
∴直线BF的解析式为:,
直线BF与AE相交于点G,
,解得:,即G(,),
线段BG的长度为:,
故选:B.
8.B
【思路指引】
根据一次函数图象与二元一次方程的关系,利用交点坐标可得方程组的解;根据两直线的系数的积为-1,可知两直线互相垂直;求得BD和AO的长,根据三角形面积计算公式,即可得到△ABD的面积;根据轴对称的性质以及两点之间,线段最短,即可得到当PA+PC的值最小时,点P的坐标为(0,1).
【详解详析】
解:①∵直线l1:y=kx+b与直线l2:y=﹣x+m都经过C(﹣,),
∴方程组的解为,
故①正确,符合题意;
②把B(0,4),C(﹣,)代入直线l1:y=kx+b,可得,解得,
∴直线l1:y=2x+4,
又∵直线l2:y=﹣x+m,
∴直线l1与直线l2互相垂直,即∠BCD=90°,
∴△BCD为直角三角形,
故②正确,符合题意;
③把C(﹣,)代入直线l2:y=﹣x+m,可得m=1,
y=﹣x+1中,令x=0,则y=1,
∴D(0,1),
∴BD=4﹣1=3,
在直线l1:y=2x+4中,令y=0,则x=﹣2,
∴A(﹣2,0),
∴AO=2,
∴S△ABD=×3×2=3,
故③错误,不符合题意
④点A关于y轴对称的点为A'(2,0),
由点C、A′的坐标得,直线CA′的表达式为:y=﹣x+1,
令x=0,则y=1,
∴当PA+PC的值最小时,点P的坐标为(0,1),
故④正确,符合题意;
故选:B.
9.B
【思路指引】
先求出平移后的函数解析式,再联立它与另一个函数解析式求出它们的交点坐标,根据第二象限的坐标特点为,得到关于m的不等式组,解这个不等式组即可得出m的取值范围.
【详解详析】
解:将函数的图像向上平移m个单位长度后的图像的解析式为,
联立后可以得到:,
解得,
因为它们的交点在第二象限,
即,
解得,
,
故选:B.
10.C
【思路指引】
将点代入函数中,得到关于,,的关系式,将看作常数,再联立满足的等式组成二元一次方程组,将,用含的式子表示出来,此时再回代入函数中,求解出的值,最后在一次函数中令,求解出y的值,最终表示出交点坐标即可.
【详解详析】
解:将点代入函数中,
得:,
又∵,
化简可得:
此时联立方程组可得: ,
解得:,
∴点的坐标可表示为(-k,2k),
将(-k,2k)代入得:
,
解得,
∵为常数且,
∴,
此时一次函数,
令,
解得:,
∴交点坐标为.
故选:C.
二、填空题
11.
【思路指引】
首先观察函数的图象y=kx+3经过点(-3,0),然后求得k值确定函数的解析式,最后求得两图象的交点求方程组的解即可;
【详解详析】
解:根据图象知:y=kx+3经过点(-3,0),
所以-3k+3=0, 解得:k=1,
所以解析式为y=x+3,
当x=-1时,y=2,
所以两个函数图象均经过(-1,2),
所以方程组 的解为,
故答案为:.
12.或
【思路指引】
分别用m表示出点A和点B的纵坐标,用点A的纵坐标减去点B的纵坐标或用点B的纵坐标减去点A的纵坐标得到以m为未知数的方程,求解即可.
【详解详析】
解:∵点A是一次函数图象上的动点,且点A的横坐标为,
∴
∵AC⊥x轴与C,
∴
∴
∵
∴
解得,或
故答案为或
13.或
【思路指引】
分别求出A、C、D三点坐标,根据,利用坐标列式计算即可.
【详解详析】
∵由直线y=﹣x+1与直线y=﹣2x交于点A,
∴点A坐标(-1,2),
∵过点B(m,0)作y轴的平行线分别交直线y=﹣x+1、直线y=﹣2x于C、D两点,
∴点C坐标(m,1-m),点D坐标(m,-2m).
∴,
解得
故答案为或.
14.±4
【思路指引】
利用一次函数y=2x+b的图象与x轴交点和与y轴交点的特点求出坐标,以及图象与坐标轴所围成的三角形是直角三角形求解.
【详解详析】
解:∵当y=0时,0=2x+b,
∴;
当x=0时,y=b,
∴一次函数y=2x+b的图象与坐标轴所围成的三角形面积:,
解得,
故答案为:.
15.(-1,)(7,-)
【思路指引】
根据题意联立两个一次函数可确定点C的坐标,然后确定点A、点B的坐标,分两种情况讨论:①当点Q位于线段BC上时,设,求得,由此可得点Q必在点B左侧,即,可得,代入求解即可得点Q的坐标;②当点Q位于C点右侧时,设,根据图形可得,代入求解即可得点Q的坐标.
【详解详析】
解:根据题意分两种情况进行讨论,
,
解得:,
∴,
令代入得:,
令代入得:,
①当点Q位于线段BC上时,如图即点Q的位置,设,
,
∴点Q必在点B左侧,即,
,
,
,
解得:,
∴,
则,
∴;
②当点Q位于C点右侧时,如图即点Q的位置,设,
,
,
,
解得:,
则,
∴;
综上可得:或,
故答案为:或.
16.(-12,-8);(4,8)
【思路指引】
分两种情况:当点E在y轴右侧时,由条件可判定AE∥BO,容易求得E点坐标;当点E在y轴左侧时,可设E点坐标为(a,a+4),过AE作直线交x轴于点C,可表示出直线AE的解析式,可表示出C点坐标,再根据勾股定理可表示出AC的长,由条件可得到AC=BC,可得到关于a的方程,可求得E点坐标.
【详解详析】
(1)当点E在y轴右侧时,如图1,连接AE,
∵∠EAB=∠ABO,
∴AE∥OB,
∵A(0,8),
∴E点纵坐标为8,
又E点在直线y=x+4上,把y=8代入可求得x=4,
∴E点坐标为(4,8);
(2)当点E在y轴左侧时,过A、E作直线交x轴于点C,如图2,
设C(m,0),
∵∠EAB=∠ABO,
∴AC=BC,
∴(4-m)2=m2+82,
解得m=-6,
∴C(6,0)
∴直线AC的解析式为,
∵E是直线AC与y=x+4的交点
∴联立,解得
∴E(-12,-8).
综上可知,E点坐标为(4,8)或(-12,-8).
故答案为:(4,8)或(-12,-8).
17.y=
【思路指引】
过点G作GP⊥GO,交OH的延长线于点P,过点P作PN⊥AE,交AE延长线于N,设点A(-,0)则AO=,DO=2,AD=2-,由“AAS”可证△GAO≌△PNG,可得NP=AG=2-,AO=GN=,可求点P坐标,求出一次函数解析式,可求点H的纵坐标,即可求解.
【详解详析】
解:如图,过点G作GP⊥GO,交OH的延长线于点P,过点P作PN⊥AE,交AE延长线于N,
设点A(-,0)
∴AO=,
∵直线y=﹣x﹣2与x轴,y轴分别交于点D,C,
∴点D(﹣2,0),∠ADC=45°,
∴DO=2,AD=2﹣,
∵AE⊥OD,
∴∠ADG=∠AGD=45°,
∴AD=AG=2﹣,
∵GP⊥GO,∠GOH=45°,
∴∠GPO=∠GOP=45°,
∴GP=GO,
∵∠AGO+∠AOG=90°,∠AGO+∠NGP=90°,
∴∠AOG=∠NGP,
又∵∠GNP=∠GAO=90°,GO=GP,
∴△GAO≌△PNG(AAS),
∴NP=AG=2﹣,AO=GN=,
∴AN=2,
∴点P(2﹣2,﹣2),
∴直线OP解析式为:y= x,
联立方程组
∴
∴点H的纵坐标为,
∴点E(,)
∵反比例函数y=的图象过点E,
∴k=×()=2,
∴反比例函数解析式为:y=,
故答案为:y= .
18.(-2,3).
【思路指引】
由,得到,根据直线与直线的交点坐标为,得到,进而得到,将代入中,即可求解.
【详解详析】
解:∵
∴
∵直线与直线的交点坐标为
∴
得
∴
∴
将代入中得
∴交点坐标为(-2,3)
故答案为:(-2,3).
19.2
【思路指引】
联立两函数解析式成方程组,通过解方程组找出交点坐标,再根据max{a,b}的意义即可得出函数的最小值.
【详解详析】
解:联立两函数解析式成方程组,得:,
解得:.
∴当x<﹣1时,y=max{x+3,﹣x+1}=﹣x+1>2;当x≥﹣1时,y=max{x+3,﹣x+1}=x+3≥2.
∴函数y=max{x+3,﹣x+1}最小值为2.
故答案为:2.
20.
【思路指引】
根据一次函数与二元一次方程组的关系可得,求得,再由一次函数的性质可得,则可得出关于m的一元一次不等式组,求解后即可得出结果.
【详解详析】
解:∵直线与直线交于点,
∴ ,
∴,
∴,
∵函数的值随值的增大而减小,
∴,
即,
∴或,
当时,,,此不等式组无解;
当时,,,不等式组的解集为.
∴的取值范围是.
故答案为:.
三、解答题
21.
解:(1),
,即,
又,
,
设直线的解析式为,将点代入得,
直线的解析式为.
在中,,
点、点关于直线对称,
设,,,
,
在中,,
(面积法亦可)
,
直线的解析式为.
(2)由(1)得,BC=OB=3,CD=4,BD=5,
则,
解得:,
将代入中,求得:
则,直线的解析式为:,
直线的解析式为:.
,
,
,
设直线的解析式为:,
在直线上,
,
,
直线的解析式为:,
联立得:,解得:.
故存在,.
(3)如图,设若直线、与直线夹角等于,
即为等腰直角三角形,作于,于,
则,
,,
直线过,
即,解得:,
直线的解析式为:,
设坐标为,则,,
点坐标为,
点在直线上,
,
解得:,
,.
当直线过点时,,解得:,
当直线过点时,,解得:.
所以或.
22.
解:(1)①当时,令,即,解得,此时满足题意,故.
当时,令,即,解得,此时满足题意,故.
当时,,故.
故答案为:,2,2.
②∵,,,
∴AB=4,.
∴.
∵,
∴.
∴.
∴或.
当,且时,令,即,解得,此时与点C重合,故舍去.
当,且时,令,即,解得,此时符合题意,故.
当,且时,令,即,解得,此时符合题意,故.
当,且时,令,即,解得,此时符合题意,故.
故点P坐标为或或.
(2)∵关于m的对称函数的解析式为
∴该函数图象为两个一次函数图象的一部分结合起来的图象.
∵一次函数图象与x轴最多只有一个交点,且关于m的对称函数与x轴有两个交点,
∴组成该对称函数的两个一次函数图象的部分图象都与x轴有交点.
∵对于,令y=0,即,解得x=2,
∴x=2必须在的范围之内.
∴.
∵对于,令y=0,即,解得,
∴必须在的范围之内.
∴.
∴.
∵直线y=x与关于m的对称函数有两个交点,
∴直线y=x分别与直线和各有一个交点.
对于直线y=x与直线,
联立可得解得
∴直线y=x与直线必有一交点.
对于直线y=x与直线,
联立可得解得
∵,
∴必须在的范围之内才能保证直线y=x与直线有交点.
∴.
∴.
∴m的取值范围是.
23.
解:(1)对于直线,令x=0得到y=3,令y=0,得到x=6,
∴A(6,0),B(0,3).
联立,
解得,
∴C(2,2),
(2)①设M(6-t,-(6-t)+3),N(6-t,6-t),
∴MN=|-(6-t)+3-(6-t)|=|t-6|,
∵OA=2MN,
∴6=2|t-6|,
解得t=2或6;
②∵四边形CMEN是平行四边形
∴CM∥EN,CN∥ME,
∴,,
设直线ME的解析式为,直线EN的解析式为
把M(6-t,-(6-t)+3)代入中,
∴,
把N(6-t,6-t)代入中,
∴
∴直线ME的解析式为,直线EN的解析式为
解得:
∴E的坐标为(,);
(3)∵C(2,2),
∴
当OC为菱形的边时,可得(,0),(,0),(,0),
当OC为菱形的对角线时,可得(2,0),
∴或或或时以O、Q、C、P为顶点的四边形构成菱形.
24.
(1)过点作于点,如图1,
BE是△ABO的角平分线,
设点
则,
解得
(2)如图2,
点D是射线BO上的一个动点,点D不与点B、点O重合,D点的横坐标为t,
且
,
当,,
,,
(且),
;
(3)如图3,当点D在线段OB上,
,
解得,
,
,
,
设的解析式为,
则,
解得,
,
设的解析式为,
,
,
解得,
,
交点为,
,
解得,
,
过点作于点,过点作于点,连接,
则,
BE是△ABO的角平分线,,
,
,
,
,
,
,
,
设,
,
,
,
,
,
,
即,
,
整理得:,
即,
解得,
.
25.解:(1)如图1所示,作出BC的垂直平分线交BC于点D,连接AD,
∴AD是三角形ABC的中线,
∴AC所在直线即要求的的一条面积等分线.
(2)①如图2所示,连接AC,OB交于点M.
∵OA=6,OC=4,
∴,,
∴,
∵四边形OABC是矩形,
∴矩形OABC的面积等分线必过点M,
将x=3代入中,得:
,
∴直线不过点M,
∴直线不是矩形OABC的面积等分线;
②如图所示,
由①知,矩形OABC的面积等分线必过点M(3,2),
设矩形OABC的面积等分线的解析式为y=kx+b与x轴相交于点E,与y轴相交于F,
∴3k+b=2,
∴b=2 3k,
∴矩形OABC的面积等分线的解析式为y=kx+2 3k,
令x=0,y=2 3k,
∴F(0,2 3k),
∴OF=|2 3k|,
令y=0,
∴x=,
∴E(,0),
∴OE=,
∵矩形OABC的面积等分线与坐标轴所围成的三角形面积为4,
∴,
∴OE OF=8,
∴|2 3k| ||=8,
∴k=2或k=,
∴矩形OABC的面积等分线函数表达式为y=2x 4或y=x+.
(3)如图所示,设三角形ABC面积的等分线的表达式为,交x轴于点F,交AB于点E.
∵三角形ABC面积的等分线过点D,
∴将D代入表达式得:b=-2,
∴表达式为.
将y=0代入得:x=,
∴F.
∴AF=.
∵点A的坐标为,点B的坐标为,
利用待定系数法可得AB的表达式为,
∵DE和AB交于点E,
∴联立表达式得:,
解得:.
∵,
∴,
∴,
代入得:,
整理得:,
解得:(舍去),
∴三角形ABC面积的等分线的表达式为.
(4)如图所示,
∵直线是的一条面积等分线,
由图像可知,
当或时,无论a取何值,直线都不能把的面积平分,
∴.
26.解:(1)当k=1时,直线l2为y=x+2.
解方程组,
解得,
∴P;
(2)当y=0时,kx+2k=0,
∵k≠0,
∴x=-2
∴C(-2,0),OC=2
当y=0时,,
∴x=6,
∴A(6,0),OA=6
过点P作PG⊥DF于点G,
∵,
∴PG∥x轴,
∴∠GPD=∠EAD,∠PGD=∠AED=90°,
∵点为的中点,
∴PD=AD,
在△PDG和△ADE中
,
∴△PDG≌△ADE(AAS),
∴DG = DE,
∵,
∴FG+GD=DF=2DE,
∴FG=GD,
∵PG⊥DF,
∴PD=PF,
∴∠PFD=∠PDF,
∵∠PFD+∠PCA=90°,∠PDF+∠PAC=90°,
∴∠PCA=∠PAC,
∴PC=PA,
过点P作PH⊥CA于点H,
∴CH=CA=4,
∴OH=CH-OC=4-2=2,
当x=2时,,
∴点P(2,2),
把点P代入y=kx+2k,得2k+2k=2,
∴;
(3)∵以为边向左作正方形,
∴PQ=PM,∠RQP=∠CMP=90°
在Rt△PMC和Rt△PQR中
∴Rt△PMC≌Rt△PQR(HL),
∴CM=RQ,
∴NR=NC,
设NR=NC=a,
则R(-a-2,a),
代入,得,
解得,a=8,
设P(m,n),
则,
∵ON=a+2=8+2=10,
∴NM=ON-OM=10+m,
∵PM=NM,
即10+m=,
解得m=,,
∴P.
27.(1)证明:当m=0时,直线为y=x,当x=2时y=2,此时直线经过点(2,2);
当m=1时,直线为y=2x-2,当x=2时y=2,此时直线经过点(2,2);
当m=2时,直线为y=3x-4,当x=2时y=2,此时直线经过点(2,2);
当x=2时,,
∴无论m为何值,直线,总经过点.
(2)解:当时,直线为,
∵直线与直线交于点A,
∴当时,y=3,
∴A(4,3);
(3)①如图,当x=1时,区域内函数值最小为1,最大为;
当x=2时,区域内函数值最小为,最大为2,存在整点(2,1);
当x=3时,区域内函数值最小为,最大为,存在整点(3,1)、(3,2);
故整点有(2,1)、(3,1)、(3,2)共3个;
②当区域W内恰好有三个整点时,即(2,1)、(3,1)、(3,2),且无论m为何值,直线总经过点,
∴当x=3时,,
∴.
28.解:(1)联立两直线解析式,可得
解得,即点坐标为
故答案为
(2)设,则,
线段
由题意可得:,,则
∴,解得或(舍去)
四边形COPN的面积
故答案为,
(3)设,则,
则的纵坐标为
又∵在直线上,
∴的横坐标为
即
,
由题意可得:
化简可得:或
解得或
故答案为或;
(4)由(3)得,则的横坐标为
则的纵坐标为,即
则
由(1)得
∴
故答案为
29.解:(1)∵A、B是直线与x轴,y轴的交点,
∴A点坐标为(6,0),B点坐标为(0,3);
(2)联立,
解得,
∴C点坐标为(2,2),
∵B点坐标为(0,3),
∴OB=3,
∴;
(3)假设存在点P使得△PBC是等腰三角形,
∵B(0,3),C(2,2),
∴,
设P点坐标为(0,m),则,
当PB=BC时,则,
∴,
解得,
∴此时P点坐标为或;
当PC=BC时,过点C作CD⊥BP于D,
∴D点坐标为(0,2),PD=BD,
∴PD=BD=1,
∴BP=2
∴OP=OB-BP=1,
∴P点坐标为(0,1)
当PB=PC时,
∴,
解得,
∴P点坐标为;
∴综上所述,当P点坐标为或或(0,1)或时,使得△PBC为等腰三角形.
