沪教版八年级数学下册试题 20.2一次函数图像与性质(含解析)
文档属性
| 名称 | 沪教版八年级数学下册试题 20.2一次函数图像与性质(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-04-17 00:00:00 | ||
图片预览




文档简介
20.2一次函数图像与性质
一、单选题
1.若关于的不等式组有解,则一次函数的图象一定不经过的象限是( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
2.在平面直角坐标系中,将直线沿坐标轴方向平移后,得到直线与关于坐标原点中心对称,则下列平移作法正确的是( )
A.将向右平移4个单位长度 B.将向左平移6个单位长度
C.将向上平移6个单位长度 D.将向上平移4个单位长度
3.已知点,,是直线上的三个点,则,,的大小关系是( ).
A. B. C. D.
4.已知一次函数(k,b是常数,)若,则它的图象可能是( )
A. B.
C. D.
5.在平面直角坐标系xOy中,直线y=2x+2和直线y=-2x+4分别交x轴于点A和点B,则下列直线中,与x轴的交点在线段AB上的是( )
A.y=x+2 B. C.y=4x-12 D.
6.如图,在平面直角坐标系中,△ABC的顶点A、B均在y轴上,点C在x轴上,将△ABC绕着顶点B旋转后,点C的对应点C′落在y轴上,点A的对应点A′落在反比例函数y=在第一象限的图象上.如果点B、C的坐标分别是(0,﹣4)、(﹣2,0),那么点A′的坐标是( )
A.(3,2) B.(,4) C.(2,3) D.(4,)
7.如果一次函数的图像经过第一、三、四象限,那么、应满足的条件是( )
A.,且; B.,且;
C.,且; D.,且.
8.一次函数y=(k+3)x+1中,y随x的增大而减小,则k的取值范围是( )
A.k>0 B.k<0 C.k<﹣3 D.k>﹣3
9.已知反比例函数y=,下列结论正确的是( )
A.y随x的增大而减小
B.图像的两支分别在第二、四象限
C.图像与y=3x的图像有两个交点
D.A(﹣1,3)在函数的图像上
10.如图,点A的坐标为(0,1),点B是x轴正半轴上的一动点,以AB为边作等腰Rt△ABC,使∠BAC=90°,设点B的横坐标为x,设点C的纵坐标为y,能表示y与x的函数关系的图象大致是( )
A. B. C. D.
二、填空题
11.如图,直角三角形的斜边在轴的正半轴上,点与原点重合,点的坐标是,且,若将绕着点旋转后30°,点和点分别落在点和点处,那么直线的解析式是__________.
12.一次函数的图像与轴交点的纵坐标为-3,且当时,-1,则该一次函数的解析式是__________.
13.如果一次函数的图像经过第一、二、四象限,那么常数的取值范围为____.
14.正比例函数的图象和反比例函数的图象相交于A,B两点,点A在第二象限,点A的横坐标为﹣1,作AD⊥x轴,垂足为D,O为坐标原点,S△AOD=1.若x轴上有点C,且S△ABC=4,则C点坐标为_____.
15.如图,点的坐标为,点从原点出发,以每秒个单位的速度沿轴向上移动,同时过点的直线关于直线也随之上下平移,且直线与直线平行,如果点关于直线的对称点落在坐标轴上,如果点的移动时间为秒,那么的值为_____.
16.一次函数的图像分别于x轴,y轴交于A、B,将线段AB绕点A顺时针旋转90度得到线段AC,则B、C两点的直线解析式为__________
17.一次函数图象与坐标轴围成的三角形称为该一次函数的坐标三角形.已知一次函数的坐标三角形的面积为3,则该一次函数的解析式为___________.
18.如图,正比例函数y=kx与反比例函数y=的图象交于A、C两点,AB⊥x轴于点B,CD⊥x轴于点D,若S四边形ABCD=6,则m的值是 ___.
19.在平面直角坐标系中,点A(﹣4,1)为直线y=kx(k≠0)和双曲线y=(m≠0)的一个交点,点B(﹣5,0),如果在直线y=kx上有一点P,使得S△ABP=2S△ABO,那么点P的坐标是 ___.
20.将正比例函数y=kx(k是常数,k≠0)的图象,沿着y轴的一个方向平移|k|个单位后与x轴、y轴围成一个三角形,我们称这个三角形为正比例函数y=kx的坐标轴三角形,如果一个正比例函数的图象经过第一、三象限,且它的坐标轴三角形的面积为5,那么这个正比例函数的解析式是__.
三、解答题
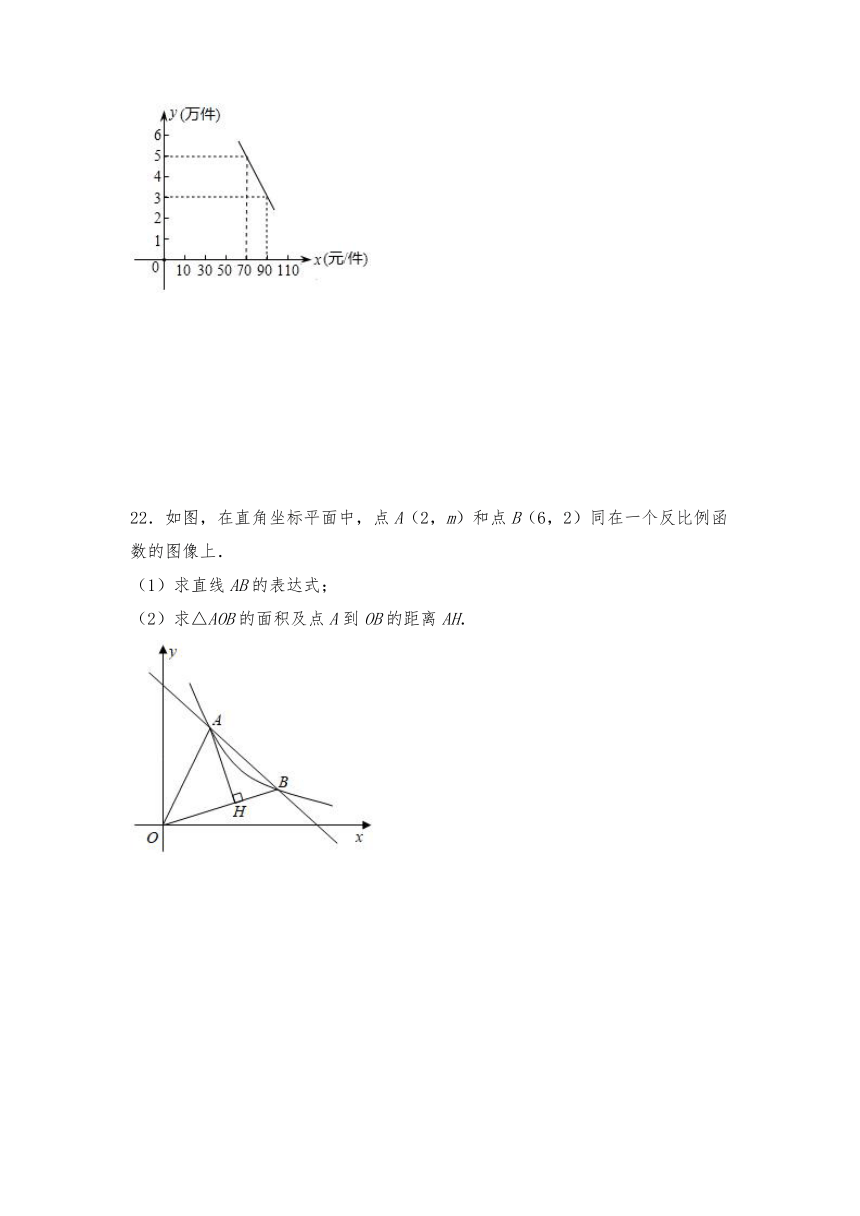
21.某商店销售一种商品.经过市场调查发现:该产品的销售单价需定在50元到110元之间较为合理,每月销售量y(万件)与销售单价x(元/件)存在如图所示的一次函数关系.根据图象提供的信息,解答下列问题:
(1)求这种商品的每月销售量y(万件)关于销售单价x(元/件)(50≤x≤110)的函数解析式;
(2)已知六月份、八月份这种商品的销售单价分别为95元/件和84元/件,且每月销售量的增长率是相同的,求这个增长率.
22.如图,在直角坐标平面中,点A(2,m)和点B(6,2)同在一个反比例函数的图像上.
(1)求直线AB的表达式;
(2)求△AOB的面积及点A到OB的距离AH.
23.已知:如图,平面直角坐标系中有一个等腰梯形,且,点在轴正半轴上,点在轴上(点在点的左侧),点在第一象限,,梯形的高为.双曲线经过点,直线经过两点.
(1)求双曲线和直线的解析式;
(2)点在双曲线上,点在轴上,如果四边形是平行四边形,请直接写出点的坐标.
24.如图,已知一次函数的图像与轴、轴分别相交于、两点,点、分别在线段、上,.
(1)求、两点的坐标;
(2)如果面积是面积的,求点的坐标.
25.已知正比例函数的图像上有一点,且点在第一象限.
(1)求点的坐标;
(2)过点作轴,点为此函数图像上异于点的点,若,求此时点的坐标.
26.已知如图,在平面直角坐标系中,点A(3,7)在正比例函数图像上.
(1)求正比例函数的解析式.
(2)点B(1,0)和点C都在x轴上,当△ABC的面积是17.5时,求点C的坐标.
(3)在(2)的条件下,将点A左右平移m个单位,得到点D,使得△AOC的面积是△ACD的面积的两倍,写出点D的坐标.(直接写出答案,不用解题过程)
27.如图,在平面直角坐标系xOy中,直线交y轴于点A,交x轴于点B,以线段AB为边作菱形ABCD(点C、D在第一象限),且点D的纵坐标为9.
(1)求点A、点B的坐标;
(2)求直线DC的解析式;
(3)除点C外,在平面直角坐标系xOy中是否还存在点P,使点A、B、D、P组成的四边形是平行四边形?若存在,请直接写出点P的坐标;若不存在,请说明理由.
28.如图,已知一次函数的图像与x轴、轴分别交于点A、B,且BC∥AO,梯形AOBC的面积为10.
(1)求点A、B、C的坐标;
(2)求直线AC的表达式.
29.已知:如图,在直角坐标平面中,点在轴的负半轴上,直线经过点,与轴相交于点,点是点关于原点的对称点,过点的直线轴,交直线于点,如果.
(1)求直线的表达式;
(2)如果点在直线上,且是等腰三角形,请求出点的坐标.
30.已知,如图,在平面直角坐标系中,一次函数与轴交于点C,与y轴交于点B,点A为y轴正半轴上的一点,将△ABC绕着顶点B旋转后,点C的对应点C’落在y轴上,点A的对应点A’恰好落在反比例函数 的图像上.
(1)求的面积;
(2)如果的值为6 (即反比例函数为),求点的坐标;
(3)如果四边形是梯形,求的值.
答案
一、单选题
1.D
【思路指引】
先解不等式组,根据不等式组有解,求得的取值范围,即可判断一次函数的图象一定不经过的象限.
【详解详析】
∵,
∴,
∵不等式组有解,
∴,
∴,
∴,
∴经过第一、二、三象限,不经过第四象限,
故选:D.
2.D
【思路指引】
先画出图象,求出直线与坐标轴交点A、B坐标,根据中心对称的性质得到对应点D、C坐标,利用待定系数法求出直线解析式,直线平移的规律即可求解.
【详解详析】
解:如图,把y=0代入得到,把x=0代入得到y=-2,
∴直线与x轴、y轴的交点分别为A、B(0,-2),
∵直线与关于坐标原点中心对称,
∴点A关于原点对称的点D的坐标为,点B关于原点对称的点C的坐标为(0,2)
设的解析式为,
则,
解得
∴的解析式为
∴直线可以看做直线向上平移4个单位得到.
故选:D
3.A
【思路指引】
结合题意,根据一次函数图像的性质分析,即可得到答案.
【详解详析】
∵直线上,随着的增加而减小,且
∴
故选:A.
4.D
【思路指引】
逐一分析各个选项的k、b的符号,结合已知条件即可做出判断
【详解详析】
解:A、由图可知k>0,b>0,且当x=-1时,-k+b<0, k>b,则|k|=k,|b|=b,可得|k|>|b|与题意不符;
B、由图可知k>0,b<0,且当x=1时,k+b>0, k>-b,则|k|=k,|b|=-b,可得|k|>|b|与题意不符;
C、由图可知当x=-1时,-k+b=0, k=b,则 |k|=|b|与题意不符;
D、由图可知k<0,b>0,且当x=1时,k+b>0, -k<b,则|k|=-k,|b|=b,可得|k|<|b|与题意相符;
故选:D
5.D
【思路指引】
先确定A,B的坐标,从而确定交点横坐标的取值范围,后逐一计算选项直线与x轴的交点,判断横坐标是否在求得的范围内,在范围内,满足条件,否则,不满足.
【详解详析】
∵直线y=2x+2和直线y=-2x+4分别交x轴于点A和点B,
∴A(-1,0),B(2,0),
∴-1≤x≤2,
∵y=x+2交x轴于点A(-2,0),且x= -2不是-1≤x≤2的解,
∴与x轴的交点不在线段AB上,
∵交x轴于点A(,0),且x= 不是-1≤x≤2的解,
∴与x轴的交点不在线段AB上,
∵y=4x-12交x轴于点A(3,0),且x= 3不是-1≤x≤2的解,
∴与x轴的交点不在线段AB上,
∵交x轴于点A(,0),且x=是-1≤x≤2的解,
∴与x轴的交点在线段AB上,
故选D.
6.A
【思路指引】
根据题意求得D的坐标,然后根据待定系数法即可求得直线A′B的解析式,与反比例函数解析式联立,解方程组即可求得A′的坐标.
【详解详析】
解:设A′B与x轴的交点为D,由题意可知D(2,0),
设直线A′B的解析式为y=kx﹣4,
把D(2,0)代入得0=2k﹣4,
解得k=2,
∴直线A′B的解析式为y=2x﹣4,
由解得或,
∴点A′的坐标是(3,2),
故选:A.
7.B
【思路指引】
根据一次函数图像的性质分析,即可得到答案.
【详解详析】
一次函数的图像经过第一、三、四象限
∴当时,;
∴当时,
∴
故选:B.
8.C
【思路指引】
根据一次函数y=(k+3)x+1中,y随x的增大而减小,推出k+3<0即可找到k的取值范围.
【详解详析】
解:∵一次函数y=(k+3)x+1中,y随x的增大而减小,
∴k+3<0,
解得:k<-3.
故A、B、D错误,
故选:C.
9.C
【思路指引】
根据反比例函数的图象性质判断即可;
【详解详析】
当和时,y随x的增大而减小,故A错误;
图像的两支分别在第一、三象限,故B错误;
图像与y=3x的图像有两个交点,故C正确;
当时,,故D错误;
故选C.
10.A
【思路指引】
根据题意作出合适的辅助线,可以先证明△ADC和△AOB的关系,即可建立y与x的函数关系,从而可以得到哪个选项是正确的.
【详解详析】
作AD∥x轴,作CD⊥AD于点D,如图所示,
由已知可得,OB=x,OA=1,∠AOB=90°,∠BAC=90°,AB=AC,点C的纵坐标是y, ∵AD∥x轴,
∴∠DAO+∠AOD=180°,
∴∠DAO=90°,
∴∠OAB+∠BAD=∠BAD+∠DAC=90°,
∴∠OAB=∠DAC,
在△OAB和△DAC中,,
∴△OAB≌△DAC(AAS),
∴OB=CD,
∴CD=x,
∵点C到x轴的距离为y,点D到x轴的距离等于点A到x的距离1,
∴y=x+1(x>0).
二、填空题
11.和
【思路指引】
先求出E、F点的坐标,再利用待定系数法即可求得.
【详解详析】
解:∵点B的坐标是(0,4),且∠A=30°.
∴AB=4,
∵在Rt△ABC中,∠BAC=30°,
∴BC=AB=2,
∴AC=,
当逆时针旋转30°后,如图所示,
∵旋转
∴EF=BC=2,AF=AC=
点E(-2,),F(0,),
∴直线EF的解析式是 y=;
当逆时针旋转30°后,如图所示,过点E、F分别作EG⊥x轴,FH⊥x轴,垂足为点G、H,
∵旋转
∴AE=AB=4,AF=AC=,∠EAF=∠BAC=30°,
∵EG∥y轴,
∴∠AEG=∠BAC=30°,
∵在Rt△EAG中,∠AEG=30°,
∴AG=AE=2,
∴EG=,
∴点E(2,),
∵∠EAF=∠BAC=30°,
∴∠FAH=90°-∠EAF-∠BAC=30°,
∵在Rt△FAH中,∠FAH=30°,
∴FH=AF=,
∴AH=,
∴点F(3,),
设直线EF的解析式为y=kx+b,
∴,解得,
∴直线EF的解析式为y=x+4,
故答案为:y=或y=x+4.
12..
【思路指引】
因为一次函数y=kx+b的图与y轴交点的纵坐标为-3,所以b=-3,根据当x=1时,y=-1,可求出解.
【详解详析】
解:根据题意设y=kx-3,且当x=1时,y=-1,
-1=k-3
∴k=2.
∴解析式为:y=2x-3.
故答案为:y=2x-3.
13.
【思路指引】
根据一次函数y=(m-2)x+m-3的图象经过第一、二、四象限,可得函数表达式中一次项系数小于0,常数项大于0,进而得到关于m的不等式组,解不等式组即可得答案取值范围.
【详解详析】
∵一次函数的图像经过第一、二、四象限,
∴,
解得:1<m<2,
故答案为:1<m<2
14.(2,0)或(﹣2,0)
【思路指引】
利用正比例函数与反比例函数图象关于原点对称求得A、B的坐标,然后根据S△ABC=4即可求得C的坐标.
【详解详析】
设反比例函数为(k≠0),正比例函数为(a≠0);
∵这两个函数的图象关于原点对称,A点的横坐标为-1,
∴A和B这两点应该是关于原点对称的,OD=1,
∵S△AOD=1,
∴,则.
∴A点坐标是(﹣1,2);B点的坐标是(1,﹣2),
设C(x,0),
∵S△ABC=4,
∴,即,
解得,
∴C(2,0)或(﹣2,0).
15.2或3
【思路指引】
找出点M关于直线l在坐标轴上的对称点E、F,如图所示.求出点E、F的坐标,然后分别求出ME、MF中点坐标,最后分别求出时间t的值.
【详解详析】
解:设直线l:y=-x+b.
如图,过点M作MF⊥直线l,交y轴于点F,交x轴于点E,则点E、F为点M在坐标轴上的对称点.
过点M作MD⊥x轴于点D,则OD=3,MD=2.
由直线l:y=-x+b可知∠PDO=∠OPD=45°,
∴∠MED=∠OEF=45°,则△MDE与△OEF均为等腰直角三角形,
∴DE=MD=2,OE=OF=1,
∴E(1,0),F(0,-1).
∵M(3,2),F(0,-1),
∴线段MF中点坐标为(,).
直线y=-x+b过点(,),则=-+b,解得:b=2,
∴t=2.
∵M(3,2),E(1,0),
∴线段ME中点坐标为(2,1).
直线y=-x+b过点(2,1),则1=-2+b,解得:b=3,
∴t=3.
故点M关于l的对称点,当t=2时,落在y轴上,当t=3时,落在x轴上.
故答案为:2或3.
16.
【思路指引】
先分别求出点的坐标,再根据旋转的性质、三角形全等的判定定理与性质求出点的坐标,然后利用待定系数法即可得.
【详解详析】
解:由题意,画图如下:
对于一次函数,
当时,,解得,即,
当时,,即,
过点作轴于点,
由旋转的性质得:,
,
轴轴,
,
,
在和中,,
,
,
,
,
设直线的解析式为,
将点代入得:,解得,
则直线的解析式为,
故答案为:.
17.或
【思路指引】
根据一次函数和坐标轴的交点坐标公式:与x轴交点,与y轴交点,求得一次函数与坐标轴的交点,然后得到底和高,利用三角形面积公式即可求解.
【详解详析】
由题意得:该函数与x轴交点,与y轴交点,
∴,
解得:,
故答案为:或.
18.3
【思路指引】
根据反比例函数k的几何意义计算即可;
【详解详析】
∵正比例函数y=kx与反比例函数y=的图象交于A、C两点,AB⊥x轴于点B,CD⊥x轴于点D,
∴,
∴,
∴,
∴,
∵反比例函数图像在一三象限,
∴;
故答案是3.
19.或
【思路指引】
根据题意作出图形,过点作轴,交直线于点,根据点的坐标求得直线和双曲线的解析式,设,进而求得的坐标,即可求得的长,当点位于点的左侧时,求得的面积,根据题意可得,当点位于点的右侧时,则,建立方程即可求得的值,从而求得的坐标
【详解详析】
如图,过点作轴,
点A(﹣4,1)为直线y=kx(k≠0)和双曲线y=(m≠0)的一个交点,
直线解析式为,双曲线为
,
,
,
,
,
,
设,
①当点在点的左侧时,根据题意可得,
,
解得,
的坐标为,
②当点在点的右侧时,
解得
综上所述,的坐标为或.
故答案为:或.
20.
【思路指引】
分别求出向上和向下平移时,与坐标轴的交点坐标,再根据它的坐标轴三角形的面积为5,求出k的值即可.
【详解详析】
解:正比例函数的图象经过第一、三象限,
,
当正比例函数是常数,的图象,沿着轴向上平移个单位时,所得函数的解析式为,
如图示:
与轴的交点坐标为,与轴的交点坐标为,
它的坐标轴三角形的面积为5,
,
,
这个正比例函数的解析式是,
当正比例函数是常数,的图象,沿着轴向下平移个单位时,所得函数的解析式为,
如图示:
与轴的交点坐标为,与轴的交点坐标为,
它的坐标轴三角形的面积为5,
,
,
这个正比例函数的解析式是,
故答案为:.
三、解答题
21.
解:(1)由题意,设y=kx+b,
图象过点(70,5)、(90,3),
∴ ,
解得: ,
∴函数解析式为:y=﹣x +12(50≤x≤110);
(2)由(1)中解析式知:
六月份的销售量为:y=﹣ ×95+12=2.5(万件),
九月份的销售量为:y=﹣×84+12=3.6(万件),
设每月销售量的增长率为x,则由题意得:
2.5(8+x)2=3.6,
解得:x=20%(负值舍去)
答:每个月的增长率为20%.
22.
解:(1)设反比例函数为,
点和点在的图象上
解得,,
点的坐标为,
设直线的表达式为,
把和代入得,
解得,
直线的表达式为;
(2)设直线与轴的交点为,
在直线为中,令,则,
,
,
,
,
,
.
23.
解:(1)如图1,过点作轴于点.
,,
四边形是等腰梯形,
轴,
四边形是矩形,
,,,
在和中,
,
.
,
梯形的高为2,
.
,,
,.
,,,,
双曲线经过点,
.
双曲线的解析式为:,
直线经过、两点,
得:,
解得:.
直线的解析式为:;
(2)如图2,四边形是平行四边形.
且.
点在轴上,
过点作轴的垂线与双曲线的交点即为点.
点的坐标为,
.
,
,
点的坐标为.
24.
解:(1)在中,
当x=0时y=,
当y=0时,,解得x=3,
根据函数关系式可得:A(3,0),B(0,);
(2)过D点作DE垂直x轴于E,
∵OA=3,OB=,AB=,
∴∠OAB=30°,
又∵CD=CA,
∴∠OCD=∠OAB+∠CDA=2∠OAB=60°,
设OC=m,
∵OA=3,
∴CD=AC=3-m,
∵∠OCD=60°,
∴∠CDE=30°,
∴CE=CD=(3-m),
DE=(3-m),
∵S△OCD=S△ABD,
∴OC DE=×OA OB,
代入数据整理得:2m2-6m+3=0,
解得m=,
∵C、D分别在OA、OB上,
∴DE<OB,AC<OA,即(3-m)<,
∴1<m<3,
∴C点的坐标为(,0).
25.
解:(1)∵点B在直线y=2x上,将B点坐标代入直线y=2x,
可得:2(m+2)=m2-4
m2-2m-8=0,
(m+2)(m-4)=0
解得:m=4或m=-2,
∵点B在第一象限内,
∴m=4,
∴点B(6,12).
(2)∵BC⊥x轴,
∴C(6,0),
设P点到直线BC的距离标为a,
∵S△BPC=S△OBC,
∴,
∴,
∴a=3,
当点P在B的右侧时,点P的横坐标为6+=9,
将x=9代入直线y=2x解析式,y=18,此时点P(9,18);
当点P在B的左侧时,点P的横坐标为6-3=3,
将x=3代入直线y=2x解析式,y=6,此时点P(3,6),
故点P坐标为(9,18)或(3,6).
26.
(1)设正比例函数的解析式为y=kx,其中k≠0
∵点A(3,7)在正比例函数图像上
∴3k=7
∴
∴正比例函数的解析式为
(2)设点,如图
∵B(1,0)
∴BC=|a-1|
∴
即
解得或
∴点C的坐标为或
(3)当时,OC=4
分别以OC和AD为底的△AOC和△ACD的高相等
∴
∴点A向左或向右平移2个单位
∴点D的坐标为(1,7)或(5,7)
当时,OC=6
分别以OC和AD为底的△AOC和△ACD的高相等
∵△AOC的面积是△ACD的面积的两倍
∴
∴点A向左或向右平移3个单位
∴点D的坐标为(0,7)或(6,7)
综上所述,点D的坐标为(0,7)或(1,7)或(5,7)或(6,7)
27.
解:(1)令中x=0,则y=4,
∴点A(0,4);
令中y=0,则﹣x+4=0,解得:x=2,
∴点B(2,0).
(2)过点D作DE⊥y轴,垂足为E,如图1所示.
∵点D的纵坐标为9,OA=4,
∴AE=5.
∵四边形是ABCD是菱形,
∴AD=AB=,
∴DE==,
∴D(,9).
∵四边形是ABCD是菱形,
∴DC∥AB,
∴设直线DC的解析式为,
∵直线DC过点D(,9),
∴b=11,
∴直线DC的解析式为.
(3)假设存在.
以点A、B、D、P组成的四边形是平行四边形还有两种情况(如图2):
①以AB为对角线时,
∵A(0,4),B(2,0),D(,9),
∴点P(0+2﹣,4+0﹣9),即(,﹣5);
②以AD为对角线时,
∵A(0,4),B(2,0),D(,9),
∴点P(0+﹣2,4+9﹣0),即(﹣,13).
故除点C外,在平面直角坐标系xOy中还存在点P,使点A、B、D、P组成的四边形是平行四边形,点P的坐标为(,﹣5)或(﹣,13).
28.
解:(1)当x=0时,y=4,
∴B(0,4),
当y=0时,即2x+4=0,
解得,x=-2,
∴A(-2,0),
∴OA=2,OB=4,
∵梯形AOBC的面积为10,
∴ .
解得,
∴点C(-3,4).
(2)设直线AC的表达式为(),
则,解得
∴直线AC的表达式为.
29.
(1)对于
当时,,则点的坐标为
设
∵
在中,,
则有
解得,即
∴点的坐标为
∵直线经过点
∴,解得
故直线的表达式为;
(2)点是点关于原点的对称点
点的坐标为
设直线上的点坐标为
则
由等腰三角形的定义,分以下三种情况:
①当时,是等腰三角形
则,解得或
或
此时,点D的坐标为或
②当时,是等腰三角形
则,解得或
或
此时,点D的坐标为或(与点重合,不能构成三角形,舍去)
③当时,是等腰三角形
则,解得
此时,点的坐标为
综上,点的坐标为点或.
30.
解:(1)因为直线,
令x=0,则y=-4,令y=0,则x=-2,
,,
,,
△的面积;
(2)设A′B与x轴的交点为D,由题意可知D(2,0),
设直线A′B的解析式为y=kx-4,
把D(2,0)代入得0=2k-4,
解得k=2,
∴直线A′B的解析式为y=2x-4,
由,解得:或,
∴点A′的坐标是(3,2);
(3)若四边形为梯形,由于点在轴的正半轴.
①证明与不平行;
∵,在中,
令,则,
又,
则,
(由于在中,,即,
所以与不平行;
②当时,可得,
即,,
又,,
所以,
过作垂线,垂足为,过作垂线,垂足为,
∵BC=,AB=8,OC=2,
∴AM==,
∴BM==,
∴,
由旋转易得△,
,,
又,
∴,
,,
又点在反比例函数图象上,
.
一、单选题
1.若关于的不等式组有解,则一次函数的图象一定不经过的象限是( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
2.在平面直角坐标系中,将直线沿坐标轴方向平移后,得到直线与关于坐标原点中心对称,则下列平移作法正确的是( )
A.将向右平移4个单位长度 B.将向左平移6个单位长度
C.将向上平移6个单位长度 D.将向上平移4个单位长度
3.已知点,,是直线上的三个点,则,,的大小关系是( ).
A. B. C. D.
4.已知一次函数(k,b是常数,)若,则它的图象可能是( )
A. B.
C. D.
5.在平面直角坐标系xOy中,直线y=2x+2和直线y=-2x+4分别交x轴于点A和点B,则下列直线中,与x轴的交点在线段AB上的是( )
A.y=x+2 B. C.y=4x-12 D.
6.如图,在平面直角坐标系中,△ABC的顶点A、B均在y轴上,点C在x轴上,将△ABC绕着顶点B旋转后,点C的对应点C′落在y轴上,点A的对应点A′落在反比例函数y=在第一象限的图象上.如果点B、C的坐标分别是(0,﹣4)、(﹣2,0),那么点A′的坐标是( )
A.(3,2) B.(,4) C.(2,3) D.(4,)
7.如果一次函数的图像经过第一、三、四象限,那么、应满足的条件是( )
A.,且; B.,且;
C.,且; D.,且.
8.一次函数y=(k+3)x+1中,y随x的增大而减小,则k的取值范围是( )
A.k>0 B.k<0 C.k<﹣3 D.k>﹣3
9.已知反比例函数y=,下列结论正确的是( )
A.y随x的增大而减小
B.图像的两支分别在第二、四象限
C.图像与y=3x的图像有两个交点
D.A(﹣1,3)在函数的图像上
10.如图,点A的坐标为(0,1),点B是x轴正半轴上的一动点,以AB为边作等腰Rt△ABC,使∠BAC=90°,设点B的横坐标为x,设点C的纵坐标为y,能表示y与x的函数关系的图象大致是( )
A. B. C. D.
二、填空题
11.如图,直角三角形的斜边在轴的正半轴上,点与原点重合,点的坐标是,且,若将绕着点旋转后30°,点和点分别落在点和点处,那么直线的解析式是__________.
12.一次函数的图像与轴交点的纵坐标为-3,且当时,-1,则该一次函数的解析式是__________.
13.如果一次函数的图像经过第一、二、四象限,那么常数的取值范围为____.
14.正比例函数的图象和反比例函数的图象相交于A,B两点,点A在第二象限,点A的横坐标为﹣1,作AD⊥x轴,垂足为D,O为坐标原点,S△AOD=1.若x轴上有点C,且S△ABC=4,则C点坐标为_____.
15.如图,点的坐标为,点从原点出发,以每秒个单位的速度沿轴向上移动,同时过点的直线关于直线也随之上下平移,且直线与直线平行,如果点关于直线的对称点落在坐标轴上,如果点的移动时间为秒,那么的值为_____.
16.一次函数的图像分别于x轴,y轴交于A、B,将线段AB绕点A顺时针旋转90度得到线段AC,则B、C两点的直线解析式为__________
17.一次函数图象与坐标轴围成的三角形称为该一次函数的坐标三角形.已知一次函数的坐标三角形的面积为3,则该一次函数的解析式为___________.
18.如图,正比例函数y=kx与反比例函数y=的图象交于A、C两点,AB⊥x轴于点B,CD⊥x轴于点D,若S四边形ABCD=6,则m的值是 ___.
19.在平面直角坐标系中,点A(﹣4,1)为直线y=kx(k≠0)和双曲线y=(m≠0)的一个交点,点B(﹣5,0),如果在直线y=kx上有一点P,使得S△ABP=2S△ABO,那么点P的坐标是 ___.
20.将正比例函数y=kx(k是常数,k≠0)的图象,沿着y轴的一个方向平移|k|个单位后与x轴、y轴围成一个三角形,我们称这个三角形为正比例函数y=kx的坐标轴三角形,如果一个正比例函数的图象经过第一、三象限,且它的坐标轴三角形的面积为5,那么这个正比例函数的解析式是__.
三、解答题
21.某商店销售一种商品.经过市场调查发现:该产品的销售单价需定在50元到110元之间较为合理,每月销售量y(万件)与销售单价x(元/件)存在如图所示的一次函数关系.根据图象提供的信息,解答下列问题:
(1)求这种商品的每月销售量y(万件)关于销售单价x(元/件)(50≤x≤110)的函数解析式;
(2)已知六月份、八月份这种商品的销售单价分别为95元/件和84元/件,且每月销售量的增长率是相同的,求这个增长率.
22.如图,在直角坐标平面中,点A(2,m)和点B(6,2)同在一个反比例函数的图像上.
(1)求直线AB的表达式;
(2)求△AOB的面积及点A到OB的距离AH.
23.已知:如图,平面直角坐标系中有一个等腰梯形,且,点在轴正半轴上,点在轴上(点在点的左侧),点在第一象限,,梯形的高为.双曲线经过点,直线经过两点.
(1)求双曲线和直线的解析式;
(2)点在双曲线上,点在轴上,如果四边形是平行四边形,请直接写出点的坐标.
24.如图,已知一次函数的图像与轴、轴分别相交于、两点,点、分别在线段、上,.
(1)求、两点的坐标;
(2)如果面积是面积的,求点的坐标.
25.已知正比例函数的图像上有一点,且点在第一象限.
(1)求点的坐标;
(2)过点作轴,点为此函数图像上异于点的点,若,求此时点的坐标.
26.已知如图,在平面直角坐标系中,点A(3,7)在正比例函数图像上.
(1)求正比例函数的解析式.
(2)点B(1,0)和点C都在x轴上,当△ABC的面积是17.5时,求点C的坐标.
(3)在(2)的条件下,将点A左右平移m个单位,得到点D,使得△AOC的面积是△ACD的面积的两倍,写出点D的坐标.(直接写出答案,不用解题过程)
27.如图,在平面直角坐标系xOy中,直线交y轴于点A,交x轴于点B,以线段AB为边作菱形ABCD(点C、D在第一象限),且点D的纵坐标为9.
(1)求点A、点B的坐标;
(2)求直线DC的解析式;
(3)除点C外,在平面直角坐标系xOy中是否还存在点P,使点A、B、D、P组成的四边形是平行四边形?若存在,请直接写出点P的坐标;若不存在,请说明理由.
28.如图,已知一次函数的图像与x轴、轴分别交于点A、B,且BC∥AO,梯形AOBC的面积为10.
(1)求点A、B、C的坐标;
(2)求直线AC的表达式.
29.已知:如图,在直角坐标平面中,点在轴的负半轴上,直线经过点,与轴相交于点,点是点关于原点的对称点,过点的直线轴,交直线于点,如果.
(1)求直线的表达式;
(2)如果点在直线上,且是等腰三角形,请求出点的坐标.
30.已知,如图,在平面直角坐标系中,一次函数与轴交于点C,与y轴交于点B,点A为y轴正半轴上的一点,将△ABC绕着顶点B旋转后,点C的对应点C’落在y轴上,点A的对应点A’恰好落在反比例函数 的图像上.
(1)求的面积;
(2)如果的值为6 (即反比例函数为),求点的坐标;
(3)如果四边形是梯形,求的值.
答案
一、单选题
1.D
【思路指引】
先解不等式组,根据不等式组有解,求得的取值范围,即可判断一次函数的图象一定不经过的象限.
【详解详析】
∵,
∴,
∵不等式组有解,
∴,
∴,
∴,
∴经过第一、二、三象限,不经过第四象限,
故选:D.
2.D
【思路指引】
先画出图象,求出直线与坐标轴交点A、B坐标,根据中心对称的性质得到对应点D、C坐标,利用待定系数法求出直线解析式,直线平移的规律即可求解.
【详解详析】
解:如图,把y=0代入得到,把x=0代入得到y=-2,
∴直线与x轴、y轴的交点分别为A、B(0,-2),
∵直线与关于坐标原点中心对称,
∴点A关于原点对称的点D的坐标为,点B关于原点对称的点C的坐标为(0,2)
设的解析式为,
则,
解得
∴的解析式为
∴直线可以看做直线向上平移4个单位得到.
故选:D
3.A
【思路指引】
结合题意,根据一次函数图像的性质分析,即可得到答案.
【详解详析】
∵直线上,随着的增加而减小,且
∴
故选:A.
4.D
【思路指引】
逐一分析各个选项的k、b的符号,结合已知条件即可做出判断
【详解详析】
解:A、由图可知k>0,b>0,且当x=-1时,-k+b<0, k>b,则|k|=k,|b|=b,可得|k|>|b|与题意不符;
B、由图可知k>0,b<0,且当x=1时,k+b>0, k>-b,则|k|=k,|b|=-b,可得|k|>|b|与题意不符;
C、由图可知当x=-1时,-k+b=0, k=b,则 |k|=|b|与题意不符;
D、由图可知k<0,b>0,且当x=1时,k+b>0, -k<b,则|k|=-k,|b|=b,可得|k|<|b|与题意相符;
故选:D
5.D
【思路指引】
先确定A,B的坐标,从而确定交点横坐标的取值范围,后逐一计算选项直线与x轴的交点,判断横坐标是否在求得的范围内,在范围内,满足条件,否则,不满足.
【详解详析】
∵直线y=2x+2和直线y=-2x+4分别交x轴于点A和点B,
∴A(-1,0),B(2,0),
∴-1≤x≤2,
∵y=x+2交x轴于点A(-2,0),且x= -2不是-1≤x≤2的解,
∴与x轴的交点不在线段AB上,
∵交x轴于点A(,0),且x= 不是-1≤x≤2的解,
∴与x轴的交点不在线段AB上,
∵y=4x-12交x轴于点A(3,0),且x= 3不是-1≤x≤2的解,
∴与x轴的交点不在线段AB上,
∵交x轴于点A(,0),且x=是-1≤x≤2的解,
∴与x轴的交点在线段AB上,
故选D.
6.A
【思路指引】
根据题意求得D的坐标,然后根据待定系数法即可求得直线A′B的解析式,与反比例函数解析式联立,解方程组即可求得A′的坐标.
【详解详析】
解:设A′B与x轴的交点为D,由题意可知D(2,0),
设直线A′B的解析式为y=kx﹣4,
把D(2,0)代入得0=2k﹣4,
解得k=2,
∴直线A′B的解析式为y=2x﹣4,
由解得或,
∴点A′的坐标是(3,2),
故选:A.
7.B
【思路指引】
根据一次函数图像的性质分析,即可得到答案.
【详解详析】
一次函数的图像经过第一、三、四象限
∴当时,;
∴当时,
∴
故选:B.
8.C
【思路指引】
根据一次函数y=(k+3)x+1中,y随x的增大而减小,推出k+3<0即可找到k的取值范围.
【详解详析】
解:∵一次函数y=(k+3)x+1中,y随x的增大而减小,
∴k+3<0,
解得:k<-3.
故A、B、D错误,
故选:C.
9.C
【思路指引】
根据反比例函数的图象性质判断即可;
【详解详析】
当和时,y随x的增大而减小,故A错误;
图像的两支分别在第一、三象限,故B错误;
图像与y=3x的图像有两个交点,故C正确;
当时,,故D错误;
故选C.
10.A
【思路指引】
根据题意作出合适的辅助线,可以先证明△ADC和△AOB的关系,即可建立y与x的函数关系,从而可以得到哪个选项是正确的.
【详解详析】
作AD∥x轴,作CD⊥AD于点D,如图所示,
由已知可得,OB=x,OA=1,∠AOB=90°,∠BAC=90°,AB=AC,点C的纵坐标是y, ∵AD∥x轴,
∴∠DAO+∠AOD=180°,
∴∠DAO=90°,
∴∠OAB+∠BAD=∠BAD+∠DAC=90°,
∴∠OAB=∠DAC,
在△OAB和△DAC中,,
∴△OAB≌△DAC(AAS),
∴OB=CD,
∴CD=x,
∵点C到x轴的距离为y,点D到x轴的距离等于点A到x的距离1,
∴y=x+1(x>0).
二、填空题
11.和
【思路指引】
先求出E、F点的坐标,再利用待定系数法即可求得.
【详解详析】
解:∵点B的坐标是(0,4),且∠A=30°.
∴AB=4,
∵在Rt△ABC中,∠BAC=30°,
∴BC=AB=2,
∴AC=,
当逆时针旋转30°后,如图所示,
∵旋转
∴EF=BC=2,AF=AC=
点E(-2,),F(0,),
∴直线EF的解析式是 y=;
当逆时针旋转30°后,如图所示,过点E、F分别作EG⊥x轴,FH⊥x轴,垂足为点G、H,
∵旋转
∴AE=AB=4,AF=AC=,∠EAF=∠BAC=30°,
∵EG∥y轴,
∴∠AEG=∠BAC=30°,
∵在Rt△EAG中,∠AEG=30°,
∴AG=AE=2,
∴EG=,
∴点E(2,),
∵∠EAF=∠BAC=30°,
∴∠FAH=90°-∠EAF-∠BAC=30°,
∵在Rt△FAH中,∠FAH=30°,
∴FH=AF=,
∴AH=,
∴点F(3,),
设直线EF的解析式为y=kx+b,
∴,解得,
∴直线EF的解析式为y=x+4,
故答案为:y=或y=x+4.
12..
【思路指引】
因为一次函数y=kx+b的图与y轴交点的纵坐标为-3,所以b=-3,根据当x=1时,y=-1,可求出解.
【详解详析】
解:根据题意设y=kx-3,且当x=1时,y=-1,
-1=k-3
∴k=2.
∴解析式为:y=2x-3.
故答案为:y=2x-3.
13.
【思路指引】
根据一次函数y=(m-2)x+m-3的图象经过第一、二、四象限,可得函数表达式中一次项系数小于0,常数项大于0,进而得到关于m的不等式组,解不等式组即可得答案取值范围.
【详解详析】
∵一次函数的图像经过第一、二、四象限,
∴,
解得:1<m<2,
故答案为:1<m<2
14.(2,0)或(﹣2,0)
【思路指引】
利用正比例函数与反比例函数图象关于原点对称求得A、B的坐标,然后根据S△ABC=4即可求得C的坐标.
【详解详析】
设反比例函数为(k≠0),正比例函数为(a≠0);
∵这两个函数的图象关于原点对称,A点的横坐标为-1,
∴A和B这两点应该是关于原点对称的,OD=1,
∵S△AOD=1,
∴,则.
∴A点坐标是(﹣1,2);B点的坐标是(1,﹣2),
设C(x,0),
∵S△ABC=4,
∴,即,
解得,
∴C(2,0)或(﹣2,0).
15.2或3
【思路指引】
找出点M关于直线l在坐标轴上的对称点E、F,如图所示.求出点E、F的坐标,然后分别求出ME、MF中点坐标,最后分别求出时间t的值.
【详解详析】
解:设直线l:y=-x+b.
如图,过点M作MF⊥直线l,交y轴于点F,交x轴于点E,则点E、F为点M在坐标轴上的对称点.
过点M作MD⊥x轴于点D,则OD=3,MD=2.
由直线l:y=-x+b可知∠PDO=∠OPD=45°,
∴∠MED=∠OEF=45°,则△MDE与△OEF均为等腰直角三角形,
∴DE=MD=2,OE=OF=1,
∴E(1,0),F(0,-1).
∵M(3,2),F(0,-1),
∴线段MF中点坐标为(,).
直线y=-x+b过点(,),则=-+b,解得:b=2,
∴t=2.
∵M(3,2),E(1,0),
∴线段ME中点坐标为(2,1).
直线y=-x+b过点(2,1),则1=-2+b,解得:b=3,
∴t=3.
故点M关于l的对称点,当t=2时,落在y轴上,当t=3时,落在x轴上.
故答案为:2或3.
16.
【思路指引】
先分别求出点的坐标,再根据旋转的性质、三角形全等的判定定理与性质求出点的坐标,然后利用待定系数法即可得.
【详解详析】
解:由题意,画图如下:
对于一次函数,
当时,,解得,即,
当时,,即,
过点作轴于点,
由旋转的性质得:,
,
轴轴,
,
,
在和中,,
,
,
,
,
设直线的解析式为,
将点代入得:,解得,
则直线的解析式为,
故答案为:.
17.或
【思路指引】
根据一次函数和坐标轴的交点坐标公式:与x轴交点,与y轴交点,求得一次函数与坐标轴的交点,然后得到底和高,利用三角形面积公式即可求解.
【详解详析】
由题意得:该函数与x轴交点,与y轴交点,
∴,
解得:,
故答案为:或.
18.3
【思路指引】
根据反比例函数k的几何意义计算即可;
【详解详析】
∵正比例函数y=kx与反比例函数y=的图象交于A、C两点,AB⊥x轴于点B,CD⊥x轴于点D,
∴,
∴,
∴,
∴,
∵反比例函数图像在一三象限,
∴;
故答案是3.
19.或
【思路指引】
根据题意作出图形,过点作轴,交直线于点,根据点的坐标求得直线和双曲线的解析式,设,进而求得的坐标,即可求得的长,当点位于点的左侧时,求得的面积,根据题意可得,当点位于点的右侧时,则,建立方程即可求得的值,从而求得的坐标
【详解详析】
如图,过点作轴,
点A(﹣4,1)为直线y=kx(k≠0)和双曲线y=(m≠0)的一个交点,
直线解析式为,双曲线为
,
,
,
,
,
,
设,
①当点在点的左侧时,根据题意可得,
,
解得,
的坐标为,
②当点在点的右侧时,
解得
综上所述,的坐标为或.
故答案为:或.
20.
【思路指引】
分别求出向上和向下平移时,与坐标轴的交点坐标,再根据它的坐标轴三角形的面积为5,求出k的值即可.
【详解详析】
解:正比例函数的图象经过第一、三象限,
,
当正比例函数是常数,的图象,沿着轴向上平移个单位时,所得函数的解析式为,
如图示:
与轴的交点坐标为,与轴的交点坐标为,
它的坐标轴三角形的面积为5,
,
,
这个正比例函数的解析式是,
当正比例函数是常数,的图象,沿着轴向下平移个单位时,所得函数的解析式为,
如图示:
与轴的交点坐标为,与轴的交点坐标为,
它的坐标轴三角形的面积为5,
,
,
这个正比例函数的解析式是,
故答案为:.
三、解答题
21.
解:(1)由题意,设y=kx+b,
图象过点(70,5)、(90,3),
∴ ,
解得: ,
∴函数解析式为:y=﹣x +12(50≤x≤110);
(2)由(1)中解析式知:
六月份的销售量为:y=﹣ ×95+12=2.5(万件),
九月份的销售量为:y=﹣×84+12=3.6(万件),
设每月销售量的增长率为x,则由题意得:
2.5(8+x)2=3.6,
解得:x=20%(负值舍去)
答:每个月的增长率为20%.
22.
解:(1)设反比例函数为,
点和点在的图象上
解得,,
点的坐标为,
设直线的表达式为,
把和代入得,
解得,
直线的表达式为;
(2)设直线与轴的交点为,
在直线为中,令,则,
,
,
,
,
,
.
23.
解:(1)如图1,过点作轴于点.
,,
四边形是等腰梯形,
轴,
四边形是矩形,
,,,
在和中,
,
.
,
梯形的高为2,
.
,,
,.
,,,,
双曲线经过点,
.
双曲线的解析式为:,
直线经过、两点,
得:,
解得:.
直线的解析式为:;
(2)如图2,四边形是平行四边形.
且.
点在轴上,
过点作轴的垂线与双曲线的交点即为点.
点的坐标为,
.
,
,
点的坐标为.
24.
解:(1)在中,
当x=0时y=,
当y=0时,,解得x=3,
根据函数关系式可得:A(3,0),B(0,);
(2)过D点作DE垂直x轴于E,
∵OA=3,OB=,AB=,
∴∠OAB=30°,
又∵CD=CA,
∴∠OCD=∠OAB+∠CDA=2∠OAB=60°,
设OC=m,
∵OA=3,
∴CD=AC=3-m,
∵∠OCD=60°,
∴∠CDE=30°,
∴CE=CD=(3-m),
DE=(3-m),
∵S△OCD=S△ABD,
∴OC DE=×OA OB,
代入数据整理得:2m2-6m+3=0,
解得m=,
∵C、D分别在OA、OB上,
∴DE<OB,AC<OA,即(3-m)<,
∴1<m<3,
∴C点的坐标为(,0).
25.
解:(1)∵点B在直线y=2x上,将B点坐标代入直线y=2x,
可得:2(m+2)=m2-4
m2-2m-8=0,
(m+2)(m-4)=0
解得:m=4或m=-2,
∵点B在第一象限内,
∴m=4,
∴点B(6,12).
(2)∵BC⊥x轴,
∴C(6,0),
设P点到直线BC的距离标为a,
∵S△BPC=S△OBC,
∴,
∴,
∴a=3,
当点P在B的右侧时,点P的横坐标为6+=9,
将x=9代入直线y=2x解析式,y=18,此时点P(9,18);
当点P在B的左侧时,点P的横坐标为6-3=3,
将x=3代入直线y=2x解析式,y=6,此时点P(3,6),
故点P坐标为(9,18)或(3,6).
26.
(1)设正比例函数的解析式为y=kx,其中k≠0
∵点A(3,7)在正比例函数图像上
∴3k=7
∴
∴正比例函数的解析式为
(2)设点,如图
∵B(1,0)
∴BC=|a-1|
∴
即
解得或
∴点C的坐标为或
(3)当时,OC=4
分别以OC和AD为底的△AOC和△ACD的高相等
∴
∴点A向左或向右平移2个单位
∴点D的坐标为(1,7)或(5,7)
当时,OC=6
分别以OC和AD为底的△AOC和△ACD的高相等
∵△AOC的面积是△ACD的面积的两倍
∴
∴点A向左或向右平移3个单位
∴点D的坐标为(0,7)或(6,7)
综上所述,点D的坐标为(0,7)或(1,7)或(5,7)或(6,7)
27.
解:(1)令中x=0,则y=4,
∴点A(0,4);
令中y=0,则﹣x+4=0,解得:x=2,
∴点B(2,0).
(2)过点D作DE⊥y轴,垂足为E,如图1所示.
∵点D的纵坐标为9,OA=4,
∴AE=5.
∵四边形是ABCD是菱形,
∴AD=AB=,
∴DE==,
∴D(,9).
∵四边形是ABCD是菱形,
∴DC∥AB,
∴设直线DC的解析式为,
∵直线DC过点D(,9),
∴b=11,
∴直线DC的解析式为.
(3)假设存在.
以点A、B、D、P组成的四边形是平行四边形还有两种情况(如图2):
①以AB为对角线时,
∵A(0,4),B(2,0),D(,9),
∴点P(0+2﹣,4+0﹣9),即(,﹣5);
②以AD为对角线时,
∵A(0,4),B(2,0),D(,9),
∴点P(0+﹣2,4+9﹣0),即(﹣,13).
故除点C外,在平面直角坐标系xOy中还存在点P,使点A、B、D、P组成的四边形是平行四边形,点P的坐标为(,﹣5)或(﹣,13).
28.
解:(1)当x=0时,y=4,
∴B(0,4),
当y=0时,即2x+4=0,
解得,x=-2,
∴A(-2,0),
∴OA=2,OB=4,
∵梯形AOBC的面积为10,
∴ .
解得,
∴点C(-3,4).
(2)设直线AC的表达式为(),
则,解得
∴直线AC的表达式为.
29.
(1)对于
当时,,则点的坐标为
设
∵
在中,,
则有
解得,即
∴点的坐标为
∵直线经过点
∴,解得
故直线的表达式为;
(2)点是点关于原点的对称点
点的坐标为
设直线上的点坐标为
则
由等腰三角形的定义,分以下三种情况:
①当时,是等腰三角形
则,解得或
或
此时,点D的坐标为或
②当时,是等腰三角形
则,解得或
或
此时,点D的坐标为或(与点重合,不能构成三角形,舍去)
③当时,是等腰三角形
则,解得
此时,点的坐标为
综上,点的坐标为点或.
30.
解:(1)因为直线,
令x=0,则y=-4,令y=0,则x=-2,
,,
,,
△的面积;
(2)设A′B与x轴的交点为D,由题意可知D(2,0),
设直线A′B的解析式为y=kx-4,
把D(2,0)代入得0=2k-4,
解得k=2,
∴直线A′B的解析式为y=2x-4,
由,解得:或,
∴点A′的坐标是(3,2);
(3)若四边形为梯形,由于点在轴的正半轴.
①证明与不平行;
∵,在中,
令,则,
又,
则,
(由于在中,,即,
所以与不平行;
②当时,可得,
即,,
又,,
所以,
过作垂线,垂足为,过作垂线,垂足为,
∵BC=,AB=8,OC=2,
∴AM==,
∴BM==,
∴,
由旋转易得△,
,,
又,
∴,
,,
又点在反比例函数图象上,
.
