人教版六年级数学下册比例的意义及基本性质课件(共31张PPT)
文档属性
| 名称 | 人教版六年级数学下册比例的意义及基本性质课件(共31张PPT) |
|
|
| 格式 | pptx | ||
| 文件大小 | 4.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-04-16 00:00:00 | ||
图片预览











文档简介
(共31张PPT)
比例的意义及基本性质
1、什么叫做比?
两个数相除又叫做两个数的比。
3、什么叫做比值?
比的前项除以后项所得的商,叫做比值。比值的是一个数。
复习:
2、说出下面比的各部分名称。
3 : 4
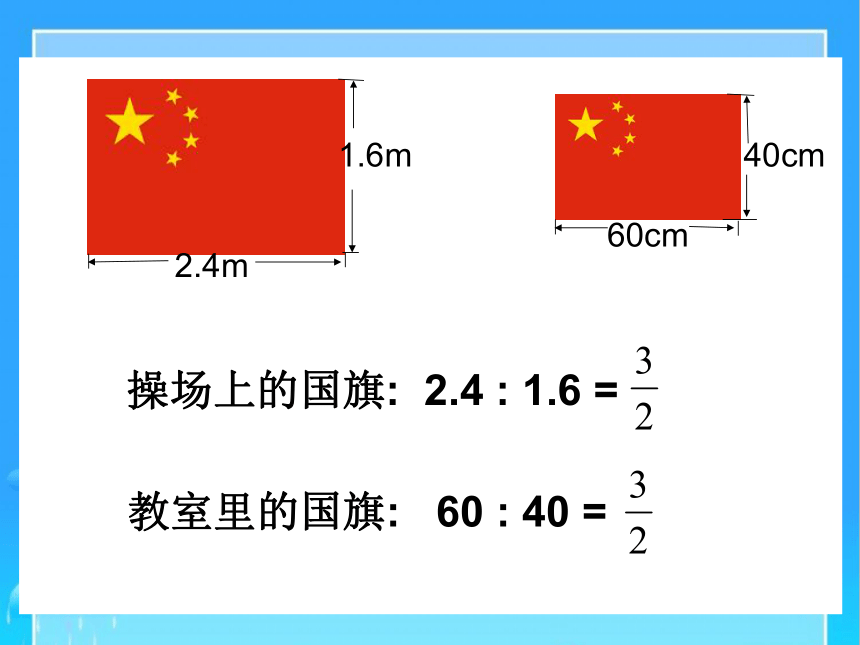
你知道国旗的长和宽吗
长2.4m,宽1.6m.
长60cm,宽40cm.
长15cm,宽10cm.
我们来看看学校里操场上和教室里的两面国旗的长宽的比值分别有什么关系。
操场上的国旗: 2.4 : 1.6 =
教室里的国旗: 60 : 40 =
2.4m
1.6m
40cm
60cm
2.4︰1.6
求出它们的比值,你发现了什么?
60︰40
=
=
或
表示两个比相等的式子叫做比例。
比例的意义:
15∶10和60∶40能组成比例吗?你是怎样判断的?
判断两个比能不能组成比例,要看它们的比值是否相等。
15 : 10 =
60 : 40 =
15 : 10 =
60 : 40
在这四面国旗的尺寸中,你还能找出哪些比可以组成比例?
比 4︰6
比例 2︰3=4︰6
比和比例有什么区别?
﹋
﹋
﹋
﹋
﹋
﹋
由两个数组成,是一个式子,
表示两个数相除。
由四个数组成,是一个等式。
表示两个比相等的式子。
判断下面的两个比能不能组成比例.
6∶10 和 9∶15
所以: 6∶10 和 9∶15
能组成比例.
因为: 6 ∶ 10 =
9∶15 =
=
判断下面的两个比能不能组成比例.
20∶5 和 1∶4
所以: 20∶5 和 1∶4
不能组成比例.
因为: 20 ∶ 5 =
1∶4 =
4
4
≠
判断下面的两个比能不能组成比例.
∶ 和 6∶4
所以: ∶ 和 6∶4
能组成比例.
因为: ∶ =
6∶4 =
=
判断下面的两个比能不能组成比例.
0.6∶0.2 和 ∶
所以: 0.6∶0.2 和 ∶
能组成比例.
因为: 0.6 ∶0.2 =
∶ =
=
3 : 4 = 1.5 : 2
3 : 1.5 = 4 : 2
4 : 3 = 2 : 1.5
1.5 : 3 = 2 : 4
1.5 : 2 = 3 : 4
4 : 2 = 3 : 1.5
2 : 1.5 = 4 : 3
2 : 4 = 1.5 : 3
2.4 ︰1.6
60 ︰40
=
内项
外项
指出下面比例的外项和内项。
4.5∶2.7 = 10 ∶6
6 ∶10
= 9 ∶15
∶
=
6 ∶4
0.6 ∶0.2
∶
=
外项
外项
内项
内项
外项
内项
外项
内项
2.4 ︰ 1.6
60︰ 40
=
外项
内项
内项积是:
1.6 × 60=96
外项积是:
2.4 × 40 = 96
2.4
40
1.6
60
×
×
=
2.4 ︰ 1.6
60 ︰ 40
=
外项
内项
=
2.4×40
1.6×60
在比例里,两个外项的积等于两个内项的积。
任意挑一组比例验证。
4.5∶2.7 = 10 ∶6
6 ∶10
= 9 ∶15
∶
=
6 ∶4
0.6 ∶0.2
∶
=
外项
外项
内项
内项
外项
内项
外项
内项
2.4︰1.6
60︰40
=
2.4
1.6
=
60
40
外项
外项
内项
内项
交叉相乘
=
2.4×40
1.6×60
2.4 ︰1.6
60︰40
=
外项
内项
在比例里,两个外项的积等于两个
内项的积,这叫做比例的基本性质.
比例的基本性质.
应用比例的基本性质,判断下面两个比能不能组成比例.
6∶3 和 8∶5
因为: 6 × 5 = 30
3 × 8 = 24
所以: 6∶3 和 8∶5
不能组成比例.
72 ≠ 81
试一试
应用比例的基本性质,判断下面两个比能不能组成比例.
0.2∶2.5 和 4∶50
因为: 0.2 × 50 = 10
2.5 × 4 = 10
所以: 0.2∶2.5 = 4∶50
能组成比例.
10 = 10
试一试
应用比例的基本性质,判断下面两个比能不能组成比例.
∶ 和 ∶
因为: × =
× =
所以: ∶ = ∶
能组成比例.
=
试一试
应用比例的基本性质,判断下面两个比能不能组成比例.
1.2∶ 和 ∶5
因为: 1.2 × 5 = 6
× =
所以: 1.2∶ 和 ∶5
不能组成比例.
6 ≠
试一试
比例的意义及基本性质
1、什么叫做比?
两个数相除又叫做两个数的比。
3、什么叫做比值?
比的前项除以后项所得的商,叫做比值。比值的是一个数。
复习:
2、说出下面比的各部分名称。
3 : 4
你知道国旗的长和宽吗
长2.4m,宽1.6m.
长60cm,宽40cm.
长15cm,宽10cm.
我们来看看学校里操场上和教室里的两面国旗的长宽的比值分别有什么关系。
操场上的国旗: 2.4 : 1.6 =
教室里的国旗: 60 : 40 =
2.4m
1.6m
40cm
60cm
2.4︰1.6
求出它们的比值,你发现了什么?
60︰40
=
=
或
表示两个比相等的式子叫做比例。
比例的意义:
15∶10和60∶40能组成比例吗?你是怎样判断的?
判断两个比能不能组成比例,要看它们的比值是否相等。
15 : 10 =
60 : 40 =
15 : 10 =
60 : 40
在这四面国旗的尺寸中,你还能找出哪些比可以组成比例?
比 4︰6
比例 2︰3=4︰6
比和比例有什么区别?
﹋
﹋
﹋
﹋
﹋
﹋
由两个数组成,是一个式子,
表示两个数相除。
由四个数组成,是一个等式。
表示两个比相等的式子。
判断下面的两个比能不能组成比例.
6∶10 和 9∶15
所以: 6∶10 和 9∶15
能组成比例.
因为: 6 ∶ 10 =
9∶15 =
=
判断下面的两个比能不能组成比例.
20∶5 和 1∶4
所以: 20∶5 和 1∶4
不能组成比例.
因为: 20 ∶ 5 =
1∶4 =
4
4
≠
判断下面的两个比能不能组成比例.
∶ 和 6∶4
所以: ∶ 和 6∶4
能组成比例.
因为: ∶ =
6∶4 =
=
判断下面的两个比能不能组成比例.
0.6∶0.2 和 ∶
所以: 0.6∶0.2 和 ∶
能组成比例.
因为: 0.6 ∶0.2 =
∶ =
=
3 : 4 = 1.5 : 2
3 : 1.5 = 4 : 2
4 : 3 = 2 : 1.5
1.5 : 3 = 2 : 4
1.5 : 2 = 3 : 4
4 : 2 = 3 : 1.5
2 : 1.5 = 4 : 3
2 : 4 = 1.5 : 3
2.4 ︰1.6
60 ︰40
=
内项
外项
指出下面比例的外项和内项。
4.5∶2.7 = 10 ∶6
6 ∶10
= 9 ∶15
∶
=
6 ∶4
0.6 ∶0.2
∶
=
外项
外项
内项
内项
外项
内项
外项
内项
2.4 ︰ 1.6
60︰ 40
=
外项
内项
内项积是:
1.6 × 60=96
外项积是:
2.4 × 40 = 96
2.4
40
1.6
60
×
×
=
2.4 ︰ 1.6
60 ︰ 40
=
外项
内项
=
2.4×40
1.6×60
在比例里,两个外项的积等于两个内项的积。
任意挑一组比例验证。
4.5∶2.7 = 10 ∶6
6 ∶10
= 9 ∶15
∶
=
6 ∶4
0.6 ∶0.2
∶
=
外项
外项
内项
内项
外项
内项
外项
内项
2.4︰1.6
60︰40
=
2.4
1.6
=
60
40
外项
外项
内项
内项
交叉相乘
=
2.4×40
1.6×60
2.4 ︰1.6
60︰40
=
外项
内项
在比例里,两个外项的积等于两个
内项的积,这叫做比例的基本性质.
比例的基本性质.
应用比例的基本性质,判断下面两个比能不能组成比例.
6∶3 和 8∶5
因为: 6 × 5 = 30
3 × 8 = 24
所以: 6∶3 和 8∶5
不能组成比例.
72 ≠ 81
试一试
应用比例的基本性质,判断下面两个比能不能组成比例.
0.2∶2.5 和 4∶50
因为: 0.2 × 50 = 10
2.5 × 4 = 10
所以: 0.2∶2.5 = 4∶50
能组成比例.
10 = 10
试一试
应用比例的基本性质,判断下面两个比能不能组成比例.
∶ 和 ∶
因为: × =
× =
所以: ∶ = ∶
能组成比例.
=
试一试
应用比例的基本性质,判断下面两个比能不能组成比例.
1.2∶ 和 ∶5
因为: 1.2 × 5 = 6
× =
所以: 1.2∶ 和 ∶5
不能组成比例.
6 ≠
试一试
