六年级下册数学人教版正比例和反比例课件(共29张PPT)
文档属性
| 名称 | 六年级下册数学人教版正比例和反比例课件(共29张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 462.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-04-16 20:41:36 | ||
图片预览






文档简介
(共29张PPT)
正比例和反比例
…...
时间(时)
路程(千米)
1
2
3
4
5
6
7
8
60
120
180
240
300
360
420
480
…...
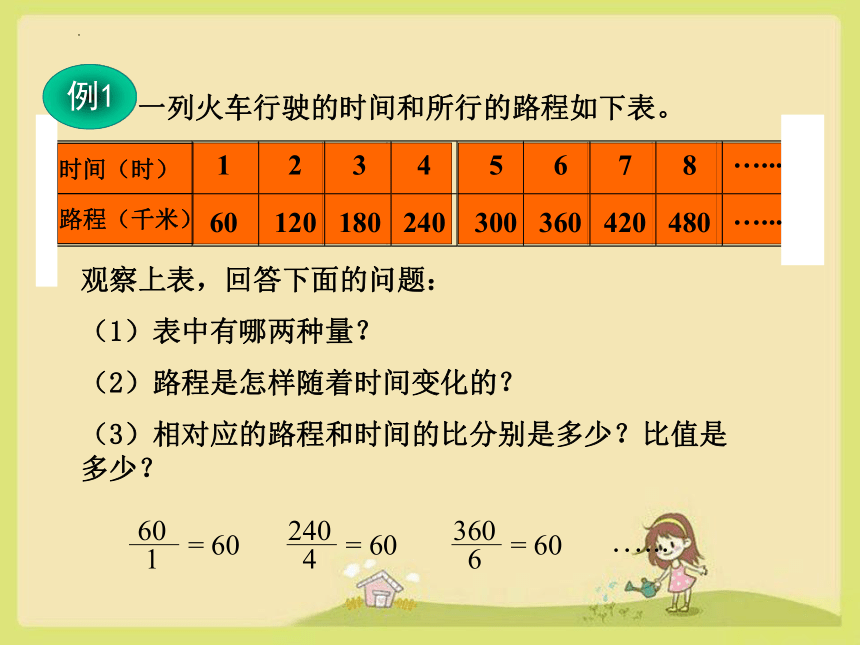
一列火车行驶的时间和所行的路程如下表。
例1
观察上表,回答下面的问题:
(1)表中有哪两种量?
(2)路程是怎样随着时间变化的?
(3)相对应的路程和时间的比分别是多少?比值是多少?
60
1
= 60
240
4
= 60
360
6
= 60
…...
一列火车行驶的时间和所行的路程如下表。
…...
时间(时)
路程(千米)
1
2
3
4
5
6
7
8
60
120
180
240
300
360
420
480
…...
例1
观察上表,回答下面的问题:
(1)表中有哪两种量?
(2)路程是怎样随着时间变化的?
(3)相对应的路程和时间的比分别是多少?比值是多少?
(1)表中有哪两种量?
(2)总价是怎样随着米数变化的?
(3)相对应的总价和米数的比各是多少?比值是多少?
…...
数量(米)
总价(元)
1
2
3
4
5
6
7
8
3.1
6.2
9.3
12.4
15.5
18.6
21.7
24.8
…...
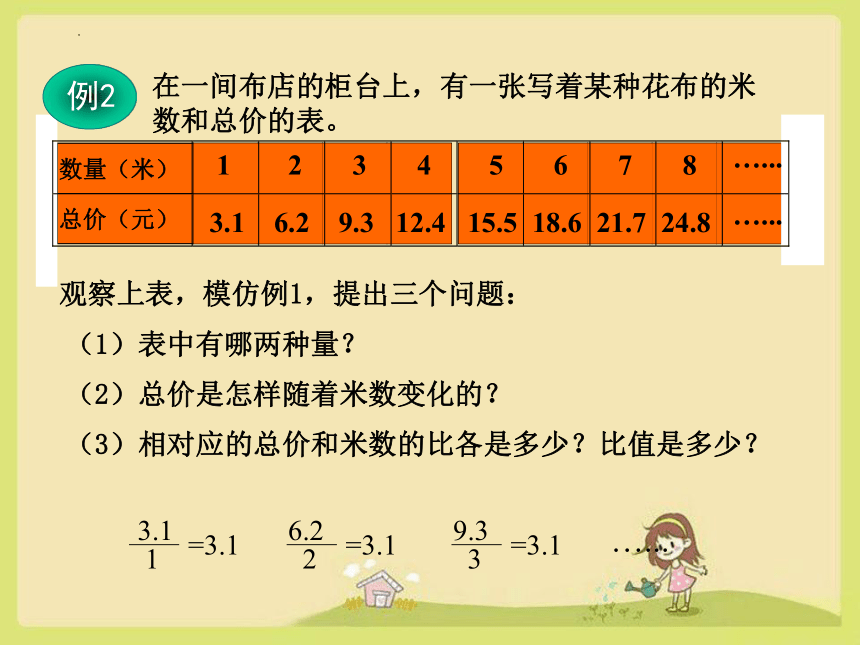
在一间布店的柜台上,有一张写着某种花布的米数和总价的表。
例2
观察上表,模仿例1,提出三个问题:
例2
3.1
1
=3.1
6.2
2
=3.1
9.3
3
=3.1
…...
(1)表中有哪两种量?
…...
数量(米)
总价(元)
1
2
3
4
5
6
7
8
3.1
6.2
9.3
12.4
15.5
18.6
21.7
24.8
…...
在一间布店的柜台上,有一张写着某种花布的米数和总价的表。
例2
观察上表,模仿例1,提出三个问题:
(2)总价是怎样随着米数变化的?
(3)相对应的总价和米数的比各是多少?比值是多少?
一列火车行驶的时间和所行的路程如下表。
…...
时间(时)
路程(千米)
1
2
3
4
5
6
7
8
60
120
180
240
300
360
420
480
…...
例1
观察上表,回答下面的问题:
(1)表中有哪两种量?
(2)路程是怎样随着时间变化的?
(3)相对应的路程和时间的比分别是多少?比值是多少?
(1)表中有哪两种量?
(2)总价是怎样随着米数变化的?
(3)相对应的总价和米数的比各是多少?比值是多少?
…...
数量(米)
总价(元)
1
2
3
4
5
6
7
8
3.1
6.2
9.3
12.4
15.5
18.6
21.7
24.8
…...
在一间布店的柜台上,有一张写着某种花布的米数和总价的表。
例2
观察上表,模仿例1,提出三个问题:
例2
一、正比例
两种相依变化的量,如果它们相对应的两个数的比的比值(也就是商)一定,这两种量就叫做成正比例量,它们之间的关系叫做正比例关系。
如果用x和y表示两种相依变化的量,用k表示它们的比值(一定),那么上面这种数量关系式可以用
=k (一定) 来表示。
y
x
时间/时 1 2 3 4 5 ---
路程/千米 100 ---
一辆汽车在高速路上行驶,速度保持在100千米/时,说一说汽车行驶的路程随时间变化的情况,并说说可以用哪些方式来表示这两个量之间的关系?
200
300
400
500
(1)可以列表
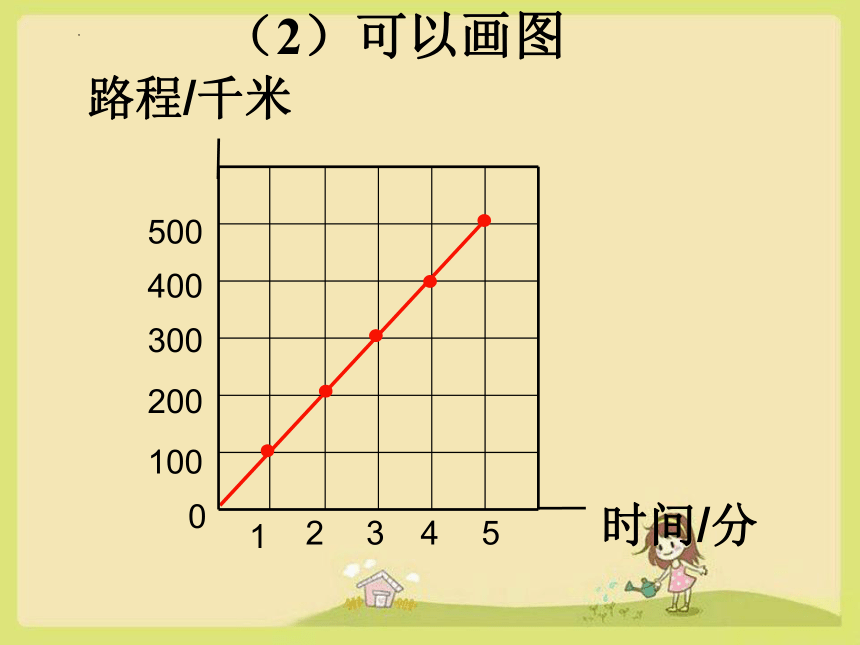
(2)可以画图
时间/分
路程/千米
0
2
4
3
5
1
100
500
200
400
300
(3)可以用式子表示
如果用t表示汽车行驶的时间,S表示汽车行驶的路程,那么
S÷t=100
你还能举出生活中或数学中一个量随另一个量变化的例子吗
输液时一小瓶葡萄糖液均匀滴落时,每分滴数与所需时间的关系如下。
每分滴数/滴 60 50 40 30 ---
时间/分 20 24 30 40 ---
…...
60×20=1200
50×24=1200
40×30=1200
30×40=1200
二、反比例
两种相依变化的量,如果它们相对应的两个数的积一定,这两种量就叫做成反比例的量,它们的关系叫做反比例关系。
如果用x和y表示两种相关联的量,用k表示它们的比值,那么上面这种数量关系式可以用
x·y=k (一定)来表示
0
2 3 4 5 6 7
1
240
40
80
120
160
200
路程(千米)
(1)
(1)
0 5 10 15 20 25 30
120
20
40
60
80
100
加工时间(时)
(2)
(2)
时间(时)
每小时加工数(个)
归纳正反比例的量
正比例 反比例
相同点
不同点
两种相依变化的量,一种量变化,另一种量也随着变化。
1)一种量扩大,另一种量也扩大,一种量缩小,另一种量也跟着 缩小。
2)相对应的两个量的比值(一定)。
1)一种量扩大,另一种量反而缩小,一种量缩小,另一种量反而扩大。
2)相对应的两个量的积(一定)
3)用字母表示:
-=k(一定)
x
y
3)用字母表示: xy=k(一定)
4)正比例图像是一条
直线。
4)反比例图像是一条
曲线。
观察下面的两个表,根据表分别填空.
例题
表1
路程(千米)
时间(时)
5
10
25
50
100
1
2
5
10
20
路程
在表1中相关联的量是
和
,
随着
变化,
是一定的.因此,
时间和路程成
关系.
时间
路程
时间
速度
正比例
观察下面的两个表,根据表分别填空.
例题
表2
速度(千米/时)
时间(时)
100
50
25
20
10
1
2
4
5
10
速度
在表2中相关联的量是
和
,
随着
变化,
是一定的.因此,
时间和速度成
关系.
时间
时间
速度
路程
反比例
思考
路程、速度和时间这三个量中每两个量之间有
什么样的比例关系?
当路程一定时,速度和时间成反比例关系.
当速度一定时,路程和时间成正比例关系.
当时间一定时,路程和速度成正比例关系.
一、填空。
1、在数量、单价和总价中:
(1)如果 一定, 和
成正比例。
(2)如果 一定, 和
成正比例。
(3)如果 一定, 和
成反比例
单价 总价
数量
总价 单价
数量
数量 总价
单价
2、已知 a × b=c。
(1)如果 一定, 和
成正比例。
(2)如果 一定, 和
成正比例。
(3)如果 一定, 和
成反比例
a b c
b a c
c a b
判断下列各题(对的打“√”错的打“X”)
(1)圆的周长与直径成正比例 ( )
圆的周长÷直径=∏
(2)圆锥体的体积一定,它的底面积与高 成反比例。 ( )
圆锥体的体积= 底面积×高×
(3)圆柱体的侧面积一定,它的底面周长与高成反比例。 ( )
圆柱体的侧面积=底面周长×高
(4)y=8X,则y和X成反比例。 ( )
y÷X=8
√
√
√
×
1
3
选择题(选择正确答案的序号填在括号里)
(1)S表示路程,T表示时间,则S=60T中,
S与T ( )
A、成正比例,B、成反比例,C、不成比例
(2)长方形的面积一定,它的长和宽( )
A、成正比例,B、成反比例,C、不成比例
(3)订《中国少年报》的份数与所需钱数( )
A、成正比例,B、成反比例,C、不成比例
A
B
A
练习与提高:
⑴如果y=8x,x和y成( )比例。
⑵如果y= ,x和y成( )比例。
正
反
判断下面每题中两种量成正比例还是反比例.
数量和总价是两种相依变化的量,它们与单价有下面的关系:
总价
数量
= 单价(一定)
所以总价和数量成正比例.
1.单价一定,数量和总价.
复习
判断下面每题中两种量成正比例还是反比例.
速度和时间是两种相依变化的量,它们与路程有下面的关系:
所以速度和时间成反比例.
2.路程一定,速度和时间.
复习
速度×时间= 路程(一定)
判断下面每题中两种量成正比例还是反比例.
边长和面积是两种相依变化的量,它们有下面的关系:
因为边长不一定,所以正方形的边长和面积不成比例.
3.正方形的边长和面积.
复习
面积
边长
= 边长
判断下面每题中两种量成正比例还是反比例.
工作效率和工作总量是两种相依变化的量,它们与工作时间有下面的关系:
所以工作效率和工作时间成正比例.
4.时间一定,工作效率和工作总量.
复习
工作总量
工作效率
= 工作时间(一定)
例 3
每袋面粉的重量一定,面粉的总重量和袋数是不是成正比例?
面粉的总重量和袋数是两种相依变化的量,
它们与每袋面
总重量
袋数
= 每袋面粉的重量(一定)
所以面粉的总重量和袋数成正比例。
粉的重量有下面的关系:
1、轮船行驶的速度一定,行驶的路程和时间。( )
2、每小时织布的米数一定,织布总米数和时间( )
3、每天看书的页数一定,看书的总页数和时间( )
4、小明跳高的高度和他的身高。( )
5、幼儿园阿姨分给每个小朋友5块糖,小朋友的人数和需要糖的总块数。( )
6、每月收入一定,每月支出的钱数和剩下的钱数。( )
7、每千克苹果的钱数一定,付出的钱数和购买苹果的数量( )
8、乒乓球总个数一定,每盒装的个数和需要的盒数。( )
9、全班人数一定,男生人数和女生人数。( )
10、三角形的面积一定,它的底和高( )
下面两种量是否成比例,成什么比例?
11、长方形的周长一定,它的长和宽( )
12、长方形的面积一定,它的长和宽( )
13、一条绳子的长一定,剪去的部分和剩下的部分( )
14、圆的直径和周长( )
15、汽车的耗油量一定,行驶的路程和耗油总量。( )
16、每支铅笔的支数相同,盒数和铅笔的总支数( )
17、教室的面积一定,教室的学生数和平均每天占的面积( )
18、每人生产的零件数一定,生产零件的总个数和需要的人数( )
19、电视机厂制造的电视机总台数一定,每天制造的台数和所有的天数( )
20、种子的总量一定,每公顷的播种量和播种的公顷数。( )
正比例和反比例
…...
时间(时)
路程(千米)
1
2
3
4
5
6
7
8
60
120
180
240
300
360
420
480
…...
一列火车行驶的时间和所行的路程如下表。
例1
观察上表,回答下面的问题:
(1)表中有哪两种量?
(2)路程是怎样随着时间变化的?
(3)相对应的路程和时间的比分别是多少?比值是多少?
60
1
= 60
240
4
= 60
360
6
= 60
…...
一列火车行驶的时间和所行的路程如下表。
…...
时间(时)
路程(千米)
1
2
3
4
5
6
7
8
60
120
180
240
300
360
420
480
…...
例1
观察上表,回答下面的问题:
(1)表中有哪两种量?
(2)路程是怎样随着时间变化的?
(3)相对应的路程和时间的比分别是多少?比值是多少?
(1)表中有哪两种量?
(2)总价是怎样随着米数变化的?
(3)相对应的总价和米数的比各是多少?比值是多少?
…...
数量(米)
总价(元)
1
2
3
4
5
6
7
8
3.1
6.2
9.3
12.4
15.5
18.6
21.7
24.8
…...
在一间布店的柜台上,有一张写着某种花布的米数和总价的表。
例2
观察上表,模仿例1,提出三个问题:
例2
3.1
1
=3.1
6.2
2
=3.1
9.3
3
=3.1
…...
(1)表中有哪两种量?
…...
数量(米)
总价(元)
1
2
3
4
5
6
7
8
3.1
6.2
9.3
12.4
15.5
18.6
21.7
24.8
…...
在一间布店的柜台上,有一张写着某种花布的米数和总价的表。
例2
观察上表,模仿例1,提出三个问题:
(2)总价是怎样随着米数变化的?
(3)相对应的总价和米数的比各是多少?比值是多少?
一列火车行驶的时间和所行的路程如下表。
…...
时间(时)
路程(千米)
1
2
3
4
5
6
7
8
60
120
180
240
300
360
420
480
…...
例1
观察上表,回答下面的问题:
(1)表中有哪两种量?
(2)路程是怎样随着时间变化的?
(3)相对应的路程和时间的比分别是多少?比值是多少?
(1)表中有哪两种量?
(2)总价是怎样随着米数变化的?
(3)相对应的总价和米数的比各是多少?比值是多少?
…...
数量(米)
总价(元)
1
2
3
4
5
6
7
8
3.1
6.2
9.3
12.4
15.5
18.6
21.7
24.8
…...
在一间布店的柜台上,有一张写着某种花布的米数和总价的表。
例2
观察上表,模仿例1,提出三个问题:
例2
一、正比例
两种相依变化的量,如果它们相对应的两个数的比的比值(也就是商)一定,这两种量就叫做成正比例量,它们之间的关系叫做正比例关系。
如果用x和y表示两种相依变化的量,用k表示它们的比值(一定),那么上面这种数量关系式可以用
=k (一定) 来表示。
y
x
时间/时 1 2 3 4 5 ---
路程/千米 100 ---
一辆汽车在高速路上行驶,速度保持在100千米/时,说一说汽车行驶的路程随时间变化的情况,并说说可以用哪些方式来表示这两个量之间的关系?
200
300
400
500
(1)可以列表
(2)可以画图
时间/分
路程/千米
0
2
4
3
5
1
100
500
200
400
300
(3)可以用式子表示
如果用t表示汽车行驶的时间,S表示汽车行驶的路程,那么
S÷t=100
你还能举出生活中或数学中一个量随另一个量变化的例子吗
输液时一小瓶葡萄糖液均匀滴落时,每分滴数与所需时间的关系如下。
每分滴数/滴 60 50 40 30 ---
时间/分 20 24 30 40 ---
…...
60×20=1200
50×24=1200
40×30=1200
30×40=1200
二、反比例
两种相依变化的量,如果它们相对应的两个数的积一定,这两种量就叫做成反比例的量,它们的关系叫做反比例关系。
如果用x和y表示两种相关联的量,用k表示它们的比值,那么上面这种数量关系式可以用
x·y=k (一定)来表示
0
2 3 4 5 6 7
1
240
40
80
120
160
200
路程(千米)
(1)
(1)
0 5 10 15 20 25 30
120
20
40
60
80
100
加工时间(时)
(2)
(2)
时间(时)
每小时加工数(个)
归纳正反比例的量
正比例 反比例
相同点
不同点
两种相依变化的量,一种量变化,另一种量也随着变化。
1)一种量扩大,另一种量也扩大,一种量缩小,另一种量也跟着 缩小。
2)相对应的两个量的比值(一定)。
1)一种量扩大,另一种量反而缩小,一种量缩小,另一种量反而扩大。
2)相对应的两个量的积(一定)
3)用字母表示:
-=k(一定)
x
y
3)用字母表示: xy=k(一定)
4)正比例图像是一条
直线。
4)反比例图像是一条
曲线。
观察下面的两个表,根据表分别填空.
例题
表1
路程(千米)
时间(时)
5
10
25
50
100
1
2
5
10
20
路程
在表1中相关联的量是
和
,
随着
变化,
是一定的.因此,
时间和路程成
关系.
时间
路程
时间
速度
正比例
观察下面的两个表,根据表分别填空.
例题
表2
速度(千米/时)
时间(时)
100
50
25
20
10
1
2
4
5
10
速度
在表2中相关联的量是
和
,
随着
变化,
是一定的.因此,
时间和速度成
关系.
时间
时间
速度
路程
反比例
思考
路程、速度和时间这三个量中每两个量之间有
什么样的比例关系?
当路程一定时,速度和时间成反比例关系.
当速度一定时,路程和时间成正比例关系.
当时间一定时,路程和速度成正比例关系.
一、填空。
1、在数量、单价和总价中:
(1)如果 一定, 和
成正比例。
(2)如果 一定, 和
成正比例。
(3)如果 一定, 和
成反比例
单价 总价
数量
总价 单价
数量
数量 总价
单价
2、已知 a × b=c。
(1)如果 一定, 和
成正比例。
(2)如果 一定, 和
成正比例。
(3)如果 一定, 和
成反比例
a b c
b a c
c a b
判断下列各题(对的打“√”错的打“X”)
(1)圆的周长与直径成正比例 ( )
圆的周长÷直径=∏
(2)圆锥体的体积一定,它的底面积与高 成反比例。 ( )
圆锥体的体积= 底面积×高×
(3)圆柱体的侧面积一定,它的底面周长与高成反比例。 ( )
圆柱体的侧面积=底面周长×高
(4)y=8X,则y和X成反比例。 ( )
y÷X=8
√
√
√
×
1
3
选择题(选择正确答案的序号填在括号里)
(1)S表示路程,T表示时间,则S=60T中,
S与T ( )
A、成正比例,B、成反比例,C、不成比例
(2)长方形的面积一定,它的长和宽( )
A、成正比例,B、成反比例,C、不成比例
(3)订《中国少年报》的份数与所需钱数( )
A、成正比例,B、成反比例,C、不成比例
A
B
A
练习与提高:
⑴如果y=8x,x和y成( )比例。
⑵如果y= ,x和y成( )比例。
正
反
判断下面每题中两种量成正比例还是反比例.
数量和总价是两种相依变化的量,它们与单价有下面的关系:
总价
数量
= 单价(一定)
所以总价和数量成正比例.
1.单价一定,数量和总价.
复习
判断下面每题中两种量成正比例还是反比例.
速度和时间是两种相依变化的量,它们与路程有下面的关系:
所以速度和时间成反比例.
2.路程一定,速度和时间.
复习
速度×时间= 路程(一定)
判断下面每题中两种量成正比例还是反比例.
边长和面积是两种相依变化的量,它们有下面的关系:
因为边长不一定,所以正方形的边长和面积不成比例.
3.正方形的边长和面积.
复习
面积
边长
= 边长
判断下面每题中两种量成正比例还是反比例.
工作效率和工作总量是两种相依变化的量,它们与工作时间有下面的关系:
所以工作效率和工作时间成正比例.
4.时间一定,工作效率和工作总量.
复习
工作总量
工作效率
= 工作时间(一定)
例 3
每袋面粉的重量一定,面粉的总重量和袋数是不是成正比例?
面粉的总重量和袋数是两种相依变化的量,
它们与每袋面
总重量
袋数
= 每袋面粉的重量(一定)
所以面粉的总重量和袋数成正比例。
粉的重量有下面的关系:
1、轮船行驶的速度一定,行驶的路程和时间。( )
2、每小时织布的米数一定,织布总米数和时间( )
3、每天看书的页数一定,看书的总页数和时间( )
4、小明跳高的高度和他的身高。( )
5、幼儿园阿姨分给每个小朋友5块糖,小朋友的人数和需要糖的总块数。( )
6、每月收入一定,每月支出的钱数和剩下的钱数。( )
7、每千克苹果的钱数一定,付出的钱数和购买苹果的数量( )
8、乒乓球总个数一定,每盒装的个数和需要的盒数。( )
9、全班人数一定,男生人数和女生人数。( )
10、三角形的面积一定,它的底和高( )
下面两种量是否成比例,成什么比例?
11、长方形的周长一定,它的长和宽( )
12、长方形的面积一定,它的长和宽( )
13、一条绳子的长一定,剪去的部分和剩下的部分( )
14、圆的直径和周长( )
15、汽车的耗油量一定,行驶的路程和耗油总量。( )
16、每支铅笔的支数相同,盒数和铅笔的总支数( )
17、教室的面积一定,教室的学生数和平均每天占的面积( )
18、每人生产的零件数一定,生产零件的总个数和需要的人数( )
19、电视机厂制造的电视机总台数一定,每天制造的台数和所有的天数( )
20、种子的总量一定,每公顷的播种量和播种的公顷数。( )
