初中数学(通用版)九年级历年中考常考知识点综合练习题01(精华)
文档属性
| 名称 | 初中数学(通用版)九年级历年中考常考知识点综合练习题01(精华) |  | |
| 格式 | docx | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-04-18 09:18:28 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
初中数学(通用版)九年级历年中考常考知识点综合练习题01(精华)
一、单选题
1.赤峰市某青少年宫门前有一座正方体雕塑,它的每个面上都有一个汉字,如图是该正方体模型的展开图,那么在正方体中,与“英”字所在面相对的面上的汉字是( )
A.塞 B.外 C.少 D.年
2.下列运算正确的是( )
A. B.
C. D.
3.若,则的值为( )
A. B. C. D.
4.如图,矩形ABCD中,E为CD的中点,连接AE并延长交BC的延长线于点F,连接BD交AF于H,AD=10 ,且tan∠EFC= ,那么AH的长为( )
A. B. C.10 D.5
5.如图,梯形ABCD中,AB∥CD,∠A=90°,E在AD上,且CE平分∠BCD,BE平分∠ABC,则下列关系式中成立的有( )
①; ②; ③;④CE2=CD×BC; ⑤BE2=AE×BC
A.2个 B.3个 C.4个 D.5个
6. 在平面直角坐标系中,二次函数的图象如图所示,现给以下结论:
;
;
;
为实数;
.
其中错误结论的个数有( )
A.个 B.个 C.个 D.个
二、多选题
7.如图,是半圆的直径,C是半圆弧的中点,D是的中点,下列结论中正确的是( )
A. B. C. D.
三、填空题
8.若关于x的一元二次方程有两个实数根,则实数a的取值范围是 .
9.已知a,b,c,d是比例线段,若,则 .
10.如图,在平面直角坐标系中,平移△ABC至△A1B1C1的位置.若顶点A(-3,4)的对应点是A1(2,5),则点B(-4,2)的对应点B1的坐标是 .
11.如图①,三翼式旋转门在圆形的空间内旋转,旋转门的三片旋转翼把空间等分成三个部分,图②是旋转门的俯视图,显示了某一时刻旋转.翼的位置.根据图②中的数据,可知的长是 m.
12.如图,将一个8cm×16cm智屏手机抽象成一个矩形ABCD,其中AB=8cm,AD=16cm,现将正在竖屏看视频的这个手机围绕它的中心R顺时针旋转90°后改为横屏看视频,其中,M是CD的中点,则图中等于45°的角有 个.(按图中所标字母写出符合条件的角)
四、计算题
13.计算:
14.
(1) .
(2)解不等式组 .
15.计算:.
16.解分式方程: .
17.已知 为整数,且满足 ,求 的值。
18.先化简,再求值: ,其中 为整数且满足不等式组
五、解答题
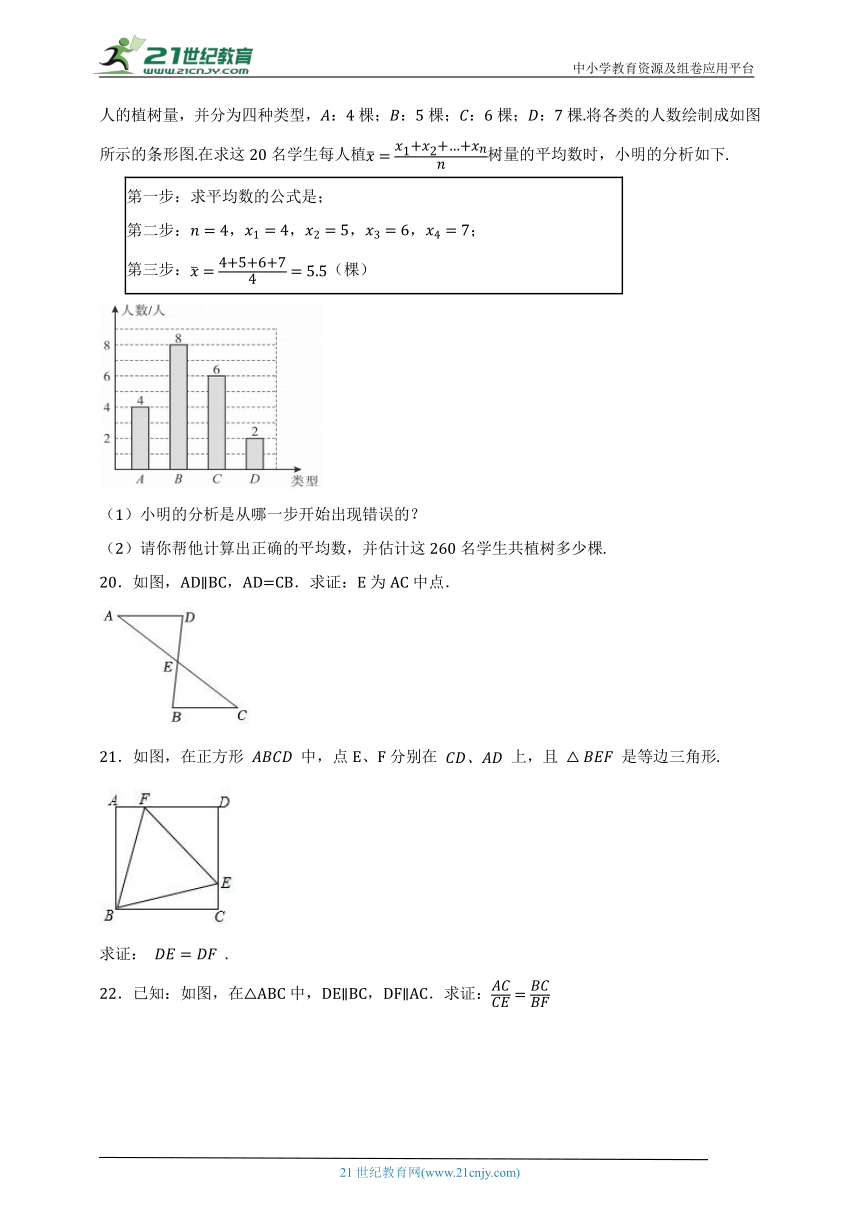
19.某校260名学生参加植树活动,要求每人植4~7棵,活动结束后随机抽查了20名学生每人的植树量,并分为四种类型,:4棵;:5棵;:6棵;:7棵.将各类的人数绘制成如图所示的条形图.在求这20名学生每人植树量的平均数时,小明的分析如下.
第一步:求平均数的公式是; 第二步:,,,,; 第三步:(棵)
(1)小明的分析是从哪一步开始出现错误的?
(2)请你帮他计算出正确的平均数,并估计这260名学生共植树多少棵.
20.如图,AD∥BC,AD=CB.求证:E为AC中点.
21.如图,在正方形 中,点E、F分别在 上,且 是等边三角形.
求证: .
22.已知:如图,在△ABC中,DE∥BC,DF∥AC.求证:
23.如图,已知AB是 O的直径,点C在 O上,过点C的直线与AB的延长线交于点P,AC=PC,∠COB=2∠PCB.
(1)求证:PC是 O的切线;
(2)求证:BC= AB;
(3)点M是弧AB的中点,CM交AB于点N,若AB=4,求MN·MC的值.
24.已知抛物线y=3ax2+2bx+c,
(Ⅰ)若a=b=1,c=﹣1,求该抛物线与x轴公共点的坐标;
(Ⅱ)若a=b=1,且当﹣1<x<1时,抛物线与x轴有且只有一个公共点,求c的取值范围;
(Ⅲ)若a+b+c=0,且x1=0时,对应的y1>0;x2=1时,对应的y2>0,试判断当0<x<1时,抛物线与x轴是否有公共点?若有,请证明你的结论;若没有,阐述理由.
六、作图题
25.如图,在平面直角坐标系中, 的三个顶点都在格点上,点A的坐标为 ,请解答下列问题:
①画出 关于x轴对称的 ,并写出点 的坐标;
②画出 关于原点对称的 ,并写出点 的坐标.﹐
26.抛物线 : 与抛物线 : 中,若 ,则称抛物线 , 为“窗帘”抛物线.
(1)已知 与 是“窗帘”抛物线,
① 的值为 ;
②在如图的坐标系中画出它们的大致图像,并直接写出它们的交点坐标.
(2)设抛物线 , , 的顶点分别为 , , ,
①判断它们是否是“窗帘”抛物线?答: (填“是”或“不是”)
②若 ,求 的值.
七、综合题
27.如图,在 中, , 分别是 , 边上的点,且 : : : .
(1)求证: ∽ ;
(2)若 ,求 的长.
28.已知函数y=(x﹣1)2;自己画出草图,根据图象回答问题:
(1)求当﹣2≤x≤﹣1时,y的取值范围;
(2)求当0≤x≤3时,y的取值范围.
29.如图,在平面直角坐标系中,O为坐标原点,抛物线y=x2+2x与x轴的另一个交点为A,把该抛物线在x轴及其下方的部分记作C1,将C1绕着点O旋转180°,得到C2,C2与x轴交于另一点B.
(1)求抛物线C2的顶点E的坐标;
(2)将C2绕着点B旋转180°得到C3,连接C1与C3的最低点,则阴影部分图形的面积为 .
30.某企业计划购买A、两种型号的机器人来搬运货物,已知每台A型机器人比每台型机器人每天少搬运10吨,且A型机器人每天搬运540吨货物与型机器人每天搬运600吨货物所需台数相同.
(1)求每台A型机器人和每台型机器人每天分别搬运货物多少吨?
(2)每台A型机器人售价1.2万元,每台型机器人售价2万元,该公司计划采购A、两种型号的机器人共30台,必须满足每天搬运的货物不低于2830吨,购买金额不超过48万元.请你求出最节省的采购方案,购买总金额最低是多少万元?
31.如图,抛物线y=-x2+bx+c与x轴相交于A(-1,0),B(5,0)两点.
(1)求抛物线的解析式;
(2)在第二象限内取一点C,作CD垂直x轴于点D,链接AC,且AD=5,CD=8,将Rt△ACD沿x轴向右平移m个单位,当点C落在抛物线上时,求m的值;
(3)在(2)的条件下,当点C第一次落在抛物线上记为点E,点P是抛物线对称轴上一点.试探究:在抛物线上是否存在点Q,使以点B、E、P、Q为顶点的四边形是平行四边形?若存在,请写出点Q的坐标;若不存在,请说明理由.
八、实践探究题
32.【阅读】
如图1,在平面直角坐标系xOy中,已知点A(a,0)(a>0),B(2,3),C(0,3).过原点O作直线l,使它经过第一、三象限,直线l与y轴的正半轴所成角设为θ,将四边形OABC的直角∠OCB沿直线l折叠,点C落在点D处,我们把这个操作过程记为FZ[θ,a].
(1)【理解】
若点D与点A重合,则这个操作过程为FZ[ , ];
(2)【尝试】
若点D恰为AB的中点(如图2),求θ;
(3)经过FZ[45°,a]操作,点B落在点E处,若点E在四边形0ABC的边AB上,求出a的值;若点E落在四边形0ABC的外部,直接写出a的取值范围;
(4)【探究】
经过FZ[θ,a]操作后,作直线CD交x轴于点G,交直线AB于点H,使得△ODG与△GAH是一对相似的等腰三角形,直接写出FZ[θ,a].
33.我们定义:
如图1,在△ABC中,把AB点绕点A顺时针旋转 得到 .把AC绕点A逆时针旋转 得到 ,连接 .当 =180°时,我们称△ 是△ABC的“旋补三角形”,△A 边 上的中线AD叫做△ABC的“旋补中线”,点A叫做“旋补中心”.
(1)[特例感知]
在图2,图3中,△A 是△ABC的“旋补三角形”,AD是△ABC的“旋补中线”
① 如图2,当△ABC为等边三角形时,AD与BC的数量关系为AD= BC.
②如图3.当∠BAC=90°,BC=8时,则AD长为
(2) [猜想论证]
在图1中,当△ABC为任意三角形时,猜想AD与BC的数量关系,并给予证明.
(3) [拓展应用]
如图4,在四边形ABCD内部恰好存在一点P,使△PDC是△PAB的“能补三角形”,自行补图形,∠C=90°,∠D=150°,BC=12,CD= ,AB=2 .直接写出△PAB的“旋补中线”长是
答案解析部分
1.【答案】B
【知识点】几何体的展开图
【解析】【解答】解:由正方体的表面展开图的“相间、Z端是对面”可知,
“英”与“外”是对面,
“雄”与“少”是对面,
“塞”与“年”是对面,
故答案为:B.
【分析】利用正方体展开图的特征求解即可。
2.【答案】D
【知识点】同底数幂的乘法;同底数幂的除法;合并同类项法则及应用;积的乘方
【解析】【解答】解:A、,故该选项不符合题意;
B、,故该选项不符合题意;
C、,故该选项不符合题意;
D、,故该选项符合题意.
故答案为:D.
【分析】合并同类项法则:同类项的系数相加减,所得的结果作为系数,字母和字母的指数不变,据此判断A;同底数幂相乘,底数不变,指数相加,据此判断B;积的乘方,先将每一项进行乘方,然后将结果相乘,据此判断C;同底数幂相除,底数不变,指数相减,.据此判断D.
3.【答案】C
【知识点】分式的值
【解析】【解答】解:;
.
故答案为:C.
【分析】待求式可变形为+1,然后将已知条件代入进行计算.
4.【答案】C
【知识点】全等三角形的判定与性质;矩形的性质;相似三角形的判定与性质
【解析】【解答】∵E为CD的中点,
∴CE=DE,
在矩形ABCD中,AD∥BC,
∴∠DAE=∠CFE,
在△ADE和△CFE中,
,
∴△ADE≌△CFE(AAS),
∴CF=AD=10 ,
∴BF=BC+CF=AD+CF=10 +10 =20 ,
∵tan∠EFC= ,
∴AB=20 × =10,
在Rt△ABF中,AF= =30,
∵AD∥BC,
∴△ADH∽△FBH,
∴ ,
∴AH= AF= ×30=10.
故答案为:C.
【分析】根据线段中点的定义可得CE=DE,根据矩形的对边平行可得AD∥BC,再根据两直线平行,内错角相等可得∠DAE=∠CFE,然后利用“角角边”证明△ADE和△CFE全等,根据全等三角形对应边相等可得CF=AD,再求出BF,然后利用tan∠EFC求出AB,再利用勾股定理列式求出AF,再求出△ADH和△FBH相似,根据相似三角形对应边成比例求出 ,再求解即可.
5.【答案】B
【知识点】直角三角形全等的判定(HL);角平分线的性质;相似三角形的判定与性质;角平分线的定义
【解析】【解答】解:过点E作EF⊥BC于点F,
∵梯形ABCD,AB∥CD,∠A=90°,
∴∠A+∠D=90°,∠DCB+∠ABC=180°,
∴∠D=90°,
∴DE⊥CD,EA⊥AB
∵CE平分∠BCD,BE平分∠ABC ,
∴DE=EF=EA,∠DCB=2∠ECB,∠ABC=2∠EBC,
∴∠ECB+∠EBC=90°,
∴∠CEB=90°;
在Rt△CDE和Rt△CFE中
∴Rt△CDE≌Rt△CFE(HL)
∴CD=CF,
同理可证AB=BF,
∵∠DEC+∠DCE=90°,∠DEC+∠AEB=90°,
∴∠DCE=∠AEB,
∵∠D=∠A=90°,
∴△CDE∽△EAB,
∴,故③正确,①②错误;
∵∠CFE=∠CBE=90°,∠ECF=∠ECB,
∴△ECF∽△BCE,
∴
∴CE2=CD×BC,故④正确;
同理可证△BEF∽△BCE,
∴BE2=BF×BC=AE×BC,故⑤正确;
∴正确结论的序号为③④⑤,一共3个.
故答案为:B
【分析】过点E作EF⊥BC于点F,利用梯形的性质和平行线的性质可证得∠A+∠D=90°,∠DCB+∠ABC=180°,利用角平分线的性质可证得DE=EF=EA,∠DCB=2∠ECB,∠ABC=2∠EBC,从而可推出∠CEB=90°;利用HL证明Rt△CDE≌Rt△CFE,利用全等三角形的性质可得到CD=CF,同理可知AB=BF;再利用有两组对应角分别相等的两三角形相似可证得△CDE∽△EAB,利用相似三角形的对应边成比例,可对①②③作出判断;同理可证得△ECF∽△BCE,利用相似三角形的对应边成比例,可证得 CE2=CD×BC,可对④作出判断;同理可证得BE2=AE×BC,可对⑤作出判断;综上所述可得到正确结论的个数.
6.【答案】A
【知识点】二次函数图象与系数的关系;二次函数y=ax^2+bx+c的性质
【解析】【解答】解:由抛物线可知:,,
对称轴,
,
,故正确;
由对称轴可知:,
,
时,,
,
,故正确;
关于的对称点为,
时,,故正确;
当时,的最小值为,
时,,
,
即,故错误;
抛物线与轴有两个交点,
,
即,
,故正确;
故选:.
【分析】利用二次函数的图象与系数的关系可得a、b、c的正负,再利用二次函数的性质逐项判断即可。
7.【答案】A,B,D
【知识点】勾股定理;垂径定理;圆心角、弧、弦的关系;圆周角定理;三角形全等的判定(ASA)
【解析】【解答】解:∵D是的中点,
∴,
∴,故A符合题意;
∵为直径,
∴,
∴,
∵C是半圆弧的中点,
∴,
∵,
∴,
∴,
∵,
∴,
∴,故B符合题意;
延长,与的延长线交于点E,如图,
∵为直径,
∴,
∵,,
∴,
∴,
∴,
∵,,
∴,故C不符合题意;
连接,
∵,,
∴,
∵,
∴,
∴,故D符合题意.
故答案为:ABD.
【分析】A、根据同圆中等弧所对的圆周角相等即可判断;
B、由AB为直径可得∠ACB=90°,由点C为半圆弧的中点可得AC=BC,根据等腰三角形的性质可得∠BOC=90°,利用余角的性质可得,即可判断;
C、延长,与的延长线交于点E,证明,可得,即得,再根据斜边大于直角边可得BC=AC<AE,即可判断;
D、连接AG,由垂直平分线的性质可得AG=BG,由勾股定理可得,据此即可判断.
8.【答案】a≤2
【知识点】一元二次方程根的判别式及应用
【解析】【解答】解:由题意,得Δ=42-4×2a≥0,
解得a≤2.
故答案为:a≤2.
【分析】一元二次方程ax2+bx+c=0(a≠0),有两个实数根的条件是△=b2-4ac≥0,依此列式计算即可.
9.【答案】
【知识点】比例线段
【解析】【解答】解:a,b,c,d是比例线段,
故答案为:.
【分析】根据比例线段的概念可得,然后将a、b、c的值代入计算可得d的值.
10.【答案】(1,3)
【知识点】坐标与图形变化﹣平移
【解析】【解答】解:∵顶点A(-3,4)的对应点是A1(2,5),
又
∴平移至的规律为:将向右平移5个单位,再向上平移1个单位即可得到
∵B(-4,2)
∴的坐标是(-4+5,2+1),即(1,3)
故答案为:(1,3)
【分析】利用点坐标平移的特征:左减右加,上加下减求解即可。
11.【答案】
【知识点】弧长的计算
【解析】【解答】解:由题意知:∠AOB=360°÷3=120°,半径为1m,
∴的长==,
故答案为:
【分析】根据弧长公式进行解答即可.
12.【答案】30
【知识点】等腰三角形的性质;正方形的性质;数学思想
【解析】【解答】解:如图,连接OR,PR,EG,FH,AC,BD,ED,DG,GB,BE,CH,AH,AF,FC,DH,CG,BF,AE.
由题意,图中有两个正方形:正方形AHCF,正方形DEBG,由此可得16个45°角,
图中有等腰直角三角形三个,△OMH,△PGM,△ORP,由此可得6个45°角,
图中∠DHG=45°,这样的角有8个,
所以一共有16+6+8=30(个),
故答案为30.
【分析】如图,连接相关线段后,找出图中的正方形、等腰直角三角形和与∠DHG一类的角,利用正方形的性质和等腰直角三角形的性质一一判断即可.
13.【答案】解:
.
【知识点】特殊角的三角函数值
【解析】【分析】先利用特殊角的三角函数值、绝对值、0指数幂和负指数幂的性质化简,再计算即可。
14.【答案】(1)解:
(2)解:解不等式①,得 x≤2,
解不等式②,得 ,
因此,原不等式组的解集为 ,
【知识点】分式的混合运算;解一元一次不等式组
【解析】【分析】(1)根据分式的混合运算化简即可;
(2)根据解不等式组的方法进行计算求解即可。
15.【答案】解:
【知识点】实数的运算
【解析】【分析】根据有理数的乘方法则、0次幂的运算法则以及绝对值的性质可得原式=1--1+-1,然后根据有理数的减法法则以及二次根式的加法法则进行计算.
16.【答案】解: ,
方程两边乘 得: ,
解得: ,
检验:当 时, .
所以原方程的解为
【知识点】分式的通分;分式方程的解及检验;解分式方程
【解析】【分析】解分式方程,先分母通分,然后合并同类项,再移项。转化为整式方程的求解。
17.【答案】解:由已知等式得 ,显然 均不为0,∴ =0或 若 ,则 .又 为整数,可求得 或 ∴ 或 ∴, 的值为0或±1.
【知识点】代数式求值;分式的加减法
【解析】【分析】首先根据异分母分式的加法法则将原式变形为,根据分式有意义的条件知 x , y 均不为0,从而得出 x + y =0或 3 x y = 2 ( x y ),由3 x y = 2 ( x y )通过配方可以得到( 3 x + 2 ) ( 3 y 2 ) = 4 ,根据x,y都是整数,从而得出;从而得出x + y = 1 或 x + y = 1 ,综上所述,从而得出答案。
18.【答案】解:原式
,
解不等式组 得 ,
则不等式组的整数解为3,
当 时,原式 .
【知识点】分式的混合运算;解一元一次不等式组
【解析】【分析】根据分式的混合运算可化解题目中的式子,再解出题中的不等式组,根据x为整数可得出x的值,从而代入可求出答案
19.【答案】(1)第二步
(2)解:(棵),
这260名学生共植树约为(棵).
【知识点】平均数及其计算
【解析】【分析】本题考查平均数的计算。题目中,总的植树量是每种类型数量乘以人数,再求和之后,除以总人数,得出每人植树量的平均数,仔细审题,正确理解题意是关键。
20.【答案】证明:∵AD∥BC,
∴∠A=∠C,∠D=∠B
在△EAD和△ECB中,
∴△EAD≌△ECB(ASA)
∴EA=EC
即E为AC的中点.
【知识点】三角形全等的判定(ASA)
【解析】【分析】利用“ASA”证明△EAD≌△ECB可得EA=EC,即可得到点E为AC的中点。
21.【答案】证明:∵四边形ABCD是正方形,
∴AB=BC=CD=AD,∠A=∠C=90°,
∵△BEF是等边三角形,
∴BE=BF,
在Rt△ABF和Rt△CBE中,
,
∴Rt△ABF≌Rt△CBE(HL),
∴AF=CE,
∴CD-CE=AD-AF,
∴DE=DF.
【知识点】直角三角形全等的判定(HL);等边三角形的性质;正方形的性质
【解析】【分析】由正方形的性质可得AB=BC=CD=AD,∠A=∠C=90°,由等边三角形的性质可得BE=BF,证明Rt△ABF≌Rt△CBE,得到AF=CE,据此证明.
22.【答案】证明:∵DE∥BC,
∴;
∵DF∥AC ,
∴;
∴
【知识点】平行线分线段成比例
【解析】【分析】根据平行于三角形一边的直线,截其他两边(或两边延长线)所得的对应线段成比例可得;;即可证明.
23.【答案】(1)证明:∵OA=OC,
∴∠A=∠ACO.
又∵∠COB=2∠A,∠COB=2∠PCB,
∴∠A=∠ACO=∠PCB.
又∵AB是⊙O的直径,
∴∠ACO+∠OCB=90°.
∴∠PCB+∠OCB=90°.
即OC⊥CP,
∵OC是⊙O的半径.
∴PC是⊙O的切线.
(2)证明:∵AC=PC,
∴∠A=∠P,
∴∠A=∠ACO=∠PCB=∠P.
又∵∠COB=∠A+∠ACO,∠CBO=∠P+∠PCB,
∴∠COB=∠CBO,
∴BC=OC.
∴BC= AB.
(3)解:连接MA,MB,
∵点M是 的中点,
∴ = ,
∴∠ACM=∠BCM.
∵∠ACM=∠ABM,
∴∠BCM=∠ABM.
∵∠BMN=∠BMC,
∴△MBN∽△MCB.
∴ ,
∴BM2=MN MC.
又∵AB是⊙O的直径, = ,
∴∠AMB=90°,AM=BM.
∵AB=4,
∴BM=2 .
∴MN MC=BM2=8.
【知识点】圆周角定理;切线的判定与性质
【解析】【分析】(1)由半径OA=OC,可得等边对等角∠A=∠ACO,则∠COB=2∠A,已知∠COB=2∠PCB,∠A=∠ACO=∠PCB.由直径所对的圆周角是直角可得∠ACO+∠OCB=90°.从而转换得到∠PCB+∠OCB=90°即可证得;(2)“等角对等边”与“等边对等角”相互运用可证OC=BC;(3)连接MA,MB,先证明△MBN∽△MCB.则 ,即BM2=MN MC.由AB是⊙O的直径, = ,AB=4,解出BM,从而可解得MN MC.
24.【答案】解:(Ⅰ)当a=b=1,c=﹣1时,抛物线为y=3x2+2x﹣1,方程3x2+2x﹣1=0的两个根为x1=﹣1, .∴该抛物线与x轴公共点的坐标是(﹣1,0)和( ,0);(Ⅱ)当a=b=1时,抛物线为y=3x2+2x+c,且与x轴有公共点.对于方程3x2+2x+c=0,判别式△=4﹣12c≥0,有c≤ .①当 时,由方程3x2+2x+ =0,解得x1=x2=﹣ .此时抛物线为y=3x2+2x+ 与x轴只有一个公共点(﹣ ,0);②当 时,x1=﹣1时,y1=3﹣2+c=1+c;x2=1时,y2=3+2+c=5+c.由已知﹣1<x<1时,该抛物线与x轴有且只有一个公共点,考虑其对称轴为 ,应有 即 ,解得﹣5<c≤﹣1.综上, 或﹣5<c≤﹣1.(6分)(Ⅲ)对于二次函数y=3ax2+2bx+c,由已知x1=0时,y1=c>0;x2=1时,y2=3a+2b+c>0,又∵a+b+c=0,∴3a+2b+c=(a+b+c)+2a+b=2a+b.∴2a+b>0.∵b=﹣a﹣c,∴2a﹣a﹣c>0,即a﹣c>0.∴a>c>0.(7分)∵关于x的一元二次方程3ax2+2bx+c=0的判别式△=4b2﹣12ac=4(a+c)2﹣12ac=4[(a﹣c)2+ac]>0,∴抛物线y=3ax2+2bx+c与x轴有两个公共点,顶点在x轴下方.又该抛物线的对称轴 ,由a+b+c=0,c>0,2a+b>0,得﹣2a<b<﹣a,∴ .又由已知x1=0时,y1>0;x2=1时,y2>0,观察图象, 可知在0<x<1范围内,该抛物线与x轴有两个公共点.
【知识点】二次函数图象与坐标轴的交点问题
【解析】【分析】(Ⅰ)把a,b,c的值代入可得抛物线的解析式,然后令y=0可得到关于x的方程,然后求得方程的两根,从而可得到抛物线与x轴交点坐标;
(Ⅱ)把a,b代入可得到抛物线的解析式,然后可求得抛物线的对称轴为x=-,然后再分为△=0和△>0两种情况求解即可;
(Ⅲ)抛物线y=3ax2+2bx+c与x轴公共点的个数就是一元二次方程3ax2+2bx+c=0的实数根的个数,接下来,判断出方程3ax2+2bx+c=0根的判别式的符号,依据判别式的符号得出相应的结论.
25.【答案】解:①如图所示:点C1的坐标(5,﹣3);
②如图所示,点C2的坐标(﹣5,3).
【知识点】作图﹣轴对称;作图﹣旋转
【解析】【分析】①利用关于x轴对称的点的坐标特点:横坐标不变,纵坐标互为相反数,据此画出△A1B1C1,写出点C1的坐标;②利用关于原点对称的点的坐标特点:横纵坐标都互为相反数,可得到点A2、B2、C2,再画出△A2B2C2,写出点C2的坐标.
26.【答案】(1)4;解:②大致图像如图, 交点坐标为: 或
(2)是;解:②∵ , ∴ . 同理 , ∴ , , ∴ . ∵ ,∴ , . ∵ ,∴ , ∴ 或
【知识点】二次函数图象上点的坐标特征;二次函数y=ax^2+bx+c的图象;二次函数y=ax^2+bx+c的性质
【解析】【解答】解:(1)①由题意 可得 求得 ;(2)①根据题干所给“窗帘”抛物线的定义 可知 满足定义所以为:是;
【分析】(1)①题干要求 的值,利用题干所给“窗帘”抛物线的定义分析即可求得,②题干要求画出大致图像,并写出交点坐标,采用描点法进行绘制,(2)①题干要求判断它们是否是“窗帘”抛物线,利用题干所给“窗帘”抛物线的定义分析即可求得,
②题干告知 ,要求 的值,分别表示D,E,F三点的坐标,并利用距离坐标公式求知答案.
27.【答案】(1)证明: : : : ,
,
,
∽ ;
(2)解: ∽ ,
,
,
,
的长为10.
【知识点】相似三角形的判定与性质
【解析】【分析】(1)根据已知条件可得,然后结合有两组边对应成比例,且夹角相等的两个三角形相似,进行证明;
(2)直接根据相似三角形对应边成比例进行计算.
28.【答案】(1)解:画出函数的y=(x﹣1)2图象如图所示:
当﹣2≤x≤﹣1时,y的取值范围是4≤y≤9
(2)解:当0≤x≤3时,y的取值范围是0≤y≤4
【知识点】二次函数y=a(x-h)^2+k的图象;二次函数y=a(x-h)^2+k的性质
【解析】【分析】(1)由函数图象得知函数对称轴为x=1, 当﹣2≤x≤﹣1时 ,函数单调递减,求出x=-2和x=-1时y的取值,确定取值区间。
(2)函数对称轴为x=1,故在x=1时,函数y取值最小;在1≤x≤3时,单调递增,即求出x=3时y的取值,即可求出y的取值范围。
29.【答案】(1)解:设抛物线y=x2+2x的顶点为G,
∵y=x2+2x=(x+1)2﹣1,
∴G(﹣1,﹣1),
∵将C1绕着点O旋转180°,得到C2,
∴点G与点E关于原点O对称,
∴E(1,1);
(2)4
【知识点】旋转的性质;关于原点对称的点的坐标特征;二次函数y=ax^2+bx+c与二次函数y=a(x-h)^2+k的转化
【解析】【解答】(2)设C3的最低点为F,
令y=0,则x2+2x=0,
解得:x=0或x=﹣2,
∴A(﹣2,0),
由题意:点A与点B关于原点O对称,
∴B(2,0),
∵将C2绕着点B旋转180°得到C3,
∴点E与点F关于原点O对称,
∴F(3,﹣1),
过点G作GH⊥OA于点H,过点F作FK⊥BD于点K,过点E作EM⊥OB于点M,如图,
∵G(﹣1,﹣1),F(3,﹣1),
∴GF∥HK,GH=FK=1,
∵GH⊥OA,FK⊥BD,
∴四边形GHKF为矩形.
∵G(﹣1,﹣1),F(3,﹣1),
∴HO=1,OK=3,
∴HK=OH+OK=4,
根据旋转不变性可得:S阴影部分=S矩形GHKF,
∴S阴影部分=HK HG=4×1=4,
故答案为:4.
【分析】(1)先求出 G(﹣1,﹣1), 再求出 点G与点E关于原点O对称, 最后求解即可;
(2)先求出B(2,0),再求出HK=OH+OK=4,最后求解即可。
30.【答案】(1)解:设每台A型机器人每天搬运货物吨,则每台型机器人每天搬运货物吨,
由题意得:,
解得:,
当时,,
是分式方程的根,
(吨),
答:每台A型机器人每天搬运货物90吨,则每台型机器人每天搬运货物100吨;
(2)解:设购买A型机器人台,购买总金额为万元,
由题意得:,
解得:,
;
,
随的增大而减小,
当时,最小,此时,
购买A型机器人17台,型机器人13台时,购买总金额最低是46.4万元.
【知识点】分式方程的实际应用;一次函数的实际应用
【解析】【分析】(1)设每台A型机器人每天搬运货物吨,则每台型机器人每天搬运货物吨,根据“ A型机器人每天搬运540吨货物与型机器人每天搬运600吨货物所需台数相同”,列出方程并解之即可;
(2)设购买A型机器人台,购买总金额为万元,根据“ 每天搬运的货物不低于2830吨,购买金额不超过48万元 ”列出不等式组,求出m的范围,根据总金额=A型机器费用+B型机器费用,列出w关于m的函数解析式,再利用一次函数的性质求解即可.
31.【答案】(1)解:∵抛物线y=﹣x2+bx+c与x轴分别交于A(﹣1,0),B(5,0)两点,
∴,解得,
∴抛物线解析式为y=﹣x2+4x+5;
(2)解:∵AD=5,且OA=1,
∴OD=6,且CD=8,
∴C(﹣6,8),
设平移后的点C的对应点为C′,则C′点的纵坐标为8,
代入抛物线解析式可得8=﹣x2+4x+5,解得x=1或x=3,
∴C′点的坐标为(1,8)或(3,8),
∵C(﹣6,8),
∴当点C落在抛物线上时,向右平移了7或9个单位,
∴m的值为7或9;
(3)解:∵y=﹣x2+4x+5=﹣(x﹣2)2+9,
∴抛物线对称轴为x=2,
∴可设P(2,t),
由(2)可知E点坐标为(1,8),
①当BE为平行四边形的边时,连接BE交对称轴于点M,过E作EF⊥x轴于点F,当BE为平行四边形的边时,过Q作对称轴的垂线,垂足为N,如图,
则∠BEF=∠BMP=∠QPN,
在△PQN和△EFB中
∴△PQN≌△EFB(AAS),
∴NQ=BF=OB﹣OF=5﹣1=4,
设Q(x,y),则QN=|x﹣2|,
∴|x﹣2|=4,解得x=﹣2或x=6,
当x=﹣2或x=6时,代入抛物线解析式可求得y=﹣7,
∴Q点坐标为(﹣2,﹣7)或(6,﹣7);
②当BE为对角线时,
∵B(5,0),E(1,8),
∴线段BE的中点坐标为(3,4),则线段PQ的中点坐标为(3,4),
设Q(x,y),且P(2,t),
∴x+2=3×2,解得x=4,把x=4代入抛物线解析式可求得y=5,
∴Q(4,5);
综上可知Q点的坐标为(﹣2,﹣7)或(6,﹣7)或(4,5).
【知识点】待定系数法求二次函数解析式;平行四边形的性质;二次函数图象上点的坐标特征;用坐标表示平移;三角形全等的判定(AAS)
【解析】【分析】(1)将点A、B的坐标代入 y=-x2+bx+c 可得b、c,据此可得抛物线的解析式;
(2)易得C(﹣6,8),设平移后的点C的对应点为C′,则C′点的纵坐标为8,将y=8代入抛物线解析式中求出x,可得C′点的坐标,然后利用点的平移规律进行解答;
(3)根据抛物线的解析式可得对称轴为x=2,设P(2,t),由(2)可知E点坐标为(1,8),①当BE为平行四边形的边时,连接BE交对称轴于点M,过E作EF⊥x轴于点F,过Q作对称轴的垂线,垂足为N,则∠BEF=∠BMP=∠QPN,证明△PQN≌△EFB,得到NQ=BF=OB-OF=4,设Q(x,y),则QN=|x-2|,据此得x,然后代入抛物线解析式中求出y,进而得点Q的坐标;②当BE为对角线时,易知线段BE的中点坐标为(3,4),线段PQ的中点坐标为(3,4),设Q(x,y),且P(2,t),则有x+2=3×2,求出x,然后代入抛物线解析式中求出y,进而可得点Q的坐标.
32.【答案】(1)45°;3
(2)解:如答图1所示,连接CD并延长,交x轴于点F.
在△BCD与△AFD中,
∴△BCD≌△AFD(ASA).
∴CD=FD,即点D为Rt△COF斜边CF的中点,
∴OD= CF=CD.
又由折叠可知,OD=OC,
∴OD=OC=CD,
∴△OCD为等边三角形,∠COD=60°,
∴θ= ∠COD=30°
(3)解:经过FZ[45°,a]操作,点B落在点E处,则点D落在x轴上,AB⊥直线l,
如答图2所示:
若点E在四边形0ABC的边AB上,
由折叠可知,OD=OC=3,DE=BC=2.
∵AB⊥直线l,θ=45°,
∴△ADE为等腰直角三角形,
∴AD=DE=2,
∴OA=OD+AD=3+2=5,
∴a=5;
由答图2可知,当0<a<5时,点E落在四边形0ABC的外部
(4)FZ[30°,2+ ],FZ[60°,2+ ].
如答图3、答图4所示.
【知识点】全等三角形的判定与性质;等边三角形的判定与性质;含30°角的直角三角形;等腰直角三角形;直角三角形斜边上的中线
【解析】【解答】解:【理解】
若点D与点A重合,由折叠性质可知,OA=OC=3,θ= ∠AOC=45°,
∴FZ[45°,3].
【分析】【理解】由折叠性质可以直接得出.【尝试】(2)如答图1所示,若点D恰为AB的中点,连接CD并延长交x轴于点F.证明△BCD≌△AFD,进而得到△OCD为等边三角形,则θ=30°;(3)如答图2所示,若点E在四边形0ABC的边AB上,则△ADE为等腰直角三角形,由此求出a=OA=OD+OA=5;由答图2进一步得到,当0<a<5时,点E落在四边形0ABC的外部.【探究】满足条件的图形有两种,如答图3、答图4所示,
33.【答案】(1);4
(2)解:结论:AD= BC.
理由:如图1中,延长AD到M,使得AD=DM,连接B′M,C′M
∵B′D=DC′,AD=DM,
∴四边形AC′MB′是平行四边形,
∴AC′=B′M=AC,
∵∠BAC+∠B′AC′=180°,∠B′AC′+∠AB′M=180°,
∴∠BAC=∠MB′A,∵AB=AB′,
∴△BAC≌△AB′M,
∴BC=AM,
∴AD= BC.
(3)
【知识点】旋转的性质;三角形的综合
【解析】【解答】解:(1)①如图2中,
∵△ABC是等边三角形,
∴AB=BC=AC=AB′=AC′,
∵DB′=DC′,
∴AD⊥B′C′,
∵∠BAC=60°,∠BAC+∠B′AC′=180°,
∴∠B′AC′=120°,
∴∠B′=∠C′=30°,
∴AD= AB’= BC,
故答案为 :;
②如图3中,
∵∠BAC=90°,∠BAC+∠B′AC′=180°,
∴∠B′AC′=∠BAC=90°,
∵AB=AB′,AC=AC′,
∴△BAC≌△B′AC′,
∴BC=B′C′,
∵B′D=DC′,
∴AD= B′C′= BC=4,
故答案为:4;
( 3 ) .
理由:如图4中,延长AD交BC的延长线于M,作BE⊥AD于E,作线段BC的垂直平分线交BE于P,交BC于F,连接PA、PD、PC,作△PCD的中线PN.
连接DF交PC于O.
∵∠ADC=150°,
∴∠MDC=30°,
在Rt△DCM中,∵CD=2 ,∠DCM=90°,∠MDC=30°,
∴CM=2,DM=4,∠M=60°,
在Rt△BEM中,∵∠BEM=90°,BM=14,∠MBE=30°,
∴EM= BM=7,
∴DE=EM-DM=3,
∵AD=6,
∴AE=DE,
∵BE⊥AD,
∴PA=PD,PB=PC,
在Rt△CDF中,∵CD=2 ,CF=6,
∴tan∠CDF= ,
∴∠CDF=60°
∴∠ADF=90°=∠AEB,
∴∠CBE=∠CFD,
∵∠CBE=∠PCF,
∴∠CFD=∠PCF,
∵∠CFD+∠CDF=90°,∠PCF+∠CPF=90°,
∴∠CPF=∠CDF=60°=∠CDF
易证△FCP≌△CFD,
∴CD=PF,∵CD∥PF,
∴四边形CDPF是矩形,
∴∠CDP=90°,
∴∠ADP=∠ADC-∠CDP=60°,
∴△ADP是等边三角形,
∴∠ADP=60°,∵∠BPF=∠CPF=60°,
∴∠BPC=120°,
∴∠APD+∠BPC=180°,
∴△PDC是△PAB的“旋补三角形”,
∵AB=2 .
∴△PAB的“旋补中线”长= AB= .
故答案为: .
【分析】(1)①首先证明△ADB′是含有30°是直角三角形,可得AD= AB′即可解决问题;②首先证明△BAC≌△B′AC′,根据直角三角形斜边中线定理即可解决问题;
(2)结论:AD= BC.如图1中,延长AD到M,使得AD=DM,连接B′M,C′M,首先证明四边形AC′MB′是平行四边形,再证明△BAC≌△AB′M,即可解决问题;
(3)存在.如图4中,延长AD交BC的延长线于M,作BE⊥AD于E,作线段BC的垂直平分线交BE于P,交BC于F,连接PA、PD、PC,作△PCD的中线PN.连接DF交PC于O.想办法证明PA=PD,PB=PC,再证明∠APD+∠BPC=180°,即可得出结论.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
初中数学(通用版)九年级历年中考常考知识点综合练习题01(精华)
一、单选题
1.赤峰市某青少年宫门前有一座正方体雕塑,它的每个面上都有一个汉字,如图是该正方体模型的展开图,那么在正方体中,与“英”字所在面相对的面上的汉字是( )
A.塞 B.外 C.少 D.年
2.下列运算正确的是( )
A. B.
C. D.
3.若,则的值为( )
A. B. C. D.
4.如图,矩形ABCD中,E为CD的中点,连接AE并延长交BC的延长线于点F,连接BD交AF于H,AD=10 ,且tan∠EFC= ,那么AH的长为( )
A. B. C.10 D.5
5.如图,梯形ABCD中,AB∥CD,∠A=90°,E在AD上,且CE平分∠BCD,BE平分∠ABC,则下列关系式中成立的有( )
①; ②; ③;④CE2=CD×BC; ⑤BE2=AE×BC
A.2个 B.3个 C.4个 D.5个
6. 在平面直角坐标系中,二次函数的图象如图所示,现给以下结论:
;
;
;
为实数;
.
其中错误结论的个数有( )
A.个 B.个 C.个 D.个
二、多选题
7.如图,是半圆的直径,C是半圆弧的中点,D是的中点,下列结论中正确的是( )
A. B. C. D.
三、填空题
8.若关于x的一元二次方程有两个实数根,则实数a的取值范围是 .
9.已知a,b,c,d是比例线段,若,则 .
10.如图,在平面直角坐标系中,平移△ABC至△A1B1C1的位置.若顶点A(-3,4)的对应点是A1(2,5),则点B(-4,2)的对应点B1的坐标是 .
11.如图①,三翼式旋转门在圆形的空间内旋转,旋转门的三片旋转翼把空间等分成三个部分,图②是旋转门的俯视图,显示了某一时刻旋转.翼的位置.根据图②中的数据,可知的长是 m.
12.如图,将一个8cm×16cm智屏手机抽象成一个矩形ABCD,其中AB=8cm,AD=16cm,现将正在竖屏看视频的这个手机围绕它的中心R顺时针旋转90°后改为横屏看视频,其中,M是CD的中点,则图中等于45°的角有 个.(按图中所标字母写出符合条件的角)
四、计算题
13.计算:
14.
(1) .
(2)解不等式组 .
15.计算:.
16.解分式方程: .
17.已知 为整数,且满足 ,求 的值。
18.先化简,再求值: ,其中 为整数且满足不等式组
五、解答题
19.某校260名学生参加植树活动,要求每人植4~7棵,活动结束后随机抽查了20名学生每人的植树量,并分为四种类型,:4棵;:5棵;:6棵;:7棵.将各类的人数绘制成如图所示的条形图.在求这20名学生每人植树量的平均数时,小明的分析如下.
第一步:求平均数的公式是; 第二步:,,,,; 第三步:(棵)
(1)小明的分析是从哪一步开始出现错误的?
(2)请你帮他计算出正确的平均数,并估计这260名学生共植树多少棵.
20.如图,AD∥BC,AD=CB.求证:E为AC中点.
21.如图,在正方形 中,点E、F分别在 上,且 是等边三角形.
求证: .
22.已知:如图,在△ABC中,DE∥BC,DF∥AC.求证:
23.如图,已知AB是 O的直径,点C在 O上,过点C的直线与AB的延长线交于点P,AC=PC,∠COB=2∠PCB.
(1)求证:PC是 O的切线;
(2)求证:BC= AB;
(3)点M是弧AB的中点,CM交AB于点N,若AB=4,求MN·MC的值.
24.已知抛物线y=3ax2+2bx+c,
(Ⅰ)若a=b=1,c=﹣1,求该抛物线与x轴公共点的坐标;
(Ⅱ)若a=b=1,且当﹣1<x<1时,抛物线与x轴有且只有一个公共点,求c的取值范围;
(Ⅲ)若a+b+c=0,且x1=0时,对应的y1>0;x2=1时,对应的y2>0,试判断当0<x<1时,抛物线与x轴是否有公共点?若有,请证明你的结论;若没有,阐述理由.
六、作图题
25.如图,在平面直角坐标系中, 的三个顶点都在格点上,点A的坐标为 ,请解答下列问题:
①画出 关于x轴对称的 ,并写出点 的坐标;
②画出 关于原点对称的 ,并写出点 的坐标.﹐
26.抛物线 : 与抛物线 : 中,若 ,则称抛物线 , 为“窗帘”抛物线.
(1)已知 与 是“窗帘”抛物线,
① 的值为 ;
②在如图的坐标系中画出它们的大致图像,并直接写出它们的交点坐标.
(2)设抛物线 , , 的顶点分别为 , , ,
①判断它们是否是“窗帘”抛物线?答: (填“是”或“不是”)
②若 ,求 的值.
七、综合题
27.如图,在 中, , 分别是 , 边上的点,且 : : : .
(1)求证: ∽ ;
(2)若 ,求 的长.
28.已知函数y=(x﹣1)2;自己画出草图,根据图象回答问题:
(1)求当﹣2≤x≤﹣1时,y的取值范围;
(2)求当0≤x≤3时,y的取值范围.
29.如图,在平面直角坐标系中,O为坐标原点,抛物线y=x2+2x与x轴的另一个交点为A,把该抛物线在x轴及其下方的部分记作C1,将C1绕着点O旋转180°,得到C2,C2与x轴交于另一点B.
(1)求抛物线C2的顶点E的坐标;
(2)将C2绕着点B旋转180°得到C3,连接C1与C3的最低点,则阴影部分图形的面积为 .
30.某企业计划购买A、两种型号的机器人来搬运货物,已知每台A型机器人比每台型机器人每天少搬运10吨,且A型机器人每天搬运540吨货物与型机器人每天搬运600吨货物所需台数相同.
(1)求每台A型机器人和每台型机器人每天分别搬运货物多少吨?
(2)每台A型机器人售价1.2万元,每台型机器人售价2万元,该公司计划采购A、两种型号的机器人共30台,必须满足每天搬运的货物不低于2830吨,购买金额不超过48万元.请你求出最节省的采购方案,购买总金额最低是多少万元?
31.如图,抛物线y=-x2+bx+c与x轴相交于A(-1,0),B(5,0)两点.
(1)求抛物线的解析式;
(2)在第二象限内取一点C,作CD垂直x轴于点D,链接AC,且AD=5,CD=8,将Rt△ACD沿x轴向右平移m个单位,当点C落在抛物线上时,求m的值;
(3)在(2)的条件下,当点C第一次落在抛物线上记为点E,点P是抛物线对称轴上一点.试探究:在抛物线上是否存在点Q,使以点B、E、P、Q为顶点的四边形是平行四边形?若存在,请写出点Q的坐标;若不存在,请说明理由.
八、实践探究题
32.【阅读】
如图1,在平面直角坐标系xOy中,已知点A(a,0)(a>0),B(2,3),C(0,3).过原点O作直线l,使它经过第一、三象限,直线l与y轴的正半轴所成角设为θ,将四边形OABC的直角∠OCB沿直线l折叠,点C落在点D处,我们把这个操作过程记为FZ[θ,a].
(1)【理解】
若点D与点A重合,则这个操作过程为FZ[ , ];
(2)【尝试】
若点D恰为AB的中点(如图2),求θ;
(3)经过FZ[45°,a]操作,点B落在点E处,若点E在四边形0ABC的边AB上,求出a的值;若点E落在四边形0ABC的外部,直接写出a的取值范围;
(4)【探究】
经过FZ[θ,a]操作后,作直线CD交x轴于点G,交直线AB于点H,使得△ODG与△GAH是一对相似的等腰三角形,直接写出FZ[θ,a].
33.我们定义:
如图1,在△ABC中,把AB点绕点A顺时针旋转 得到 .把AC绕点A逆时针旋转 得到 ,连接 .当 =180°时,我们称△ 是△ABC的“旋补三角形”,△A 边 上的中线AD叫做△ABC的“旋补中线”,点A叫做“旋补中心”.
(1)[特例感知]
在图2,图3中,△A 是△ABC的“旋补三角形”,AD是△ABC的“旋补中线”
① 如图2,当△ABC为等边三角形时,AD与BC的数量关系为AD= BC.
②如图3.当∠BAC=90°,BC=8时,则AD长为
(2) [猜想论证]
在图1中,当△ABC为任意三角形时,猜想AD与BC的数量关系,并给予证明.
(3) [拓展应用]
如图4,在四边形ABCD内部恰好存在一点P,使△PDC是△PAB的“能补三角形”,自行补图形,∠C=90°,∠D=150°,BC=12,CD= ,AB=2 .直接写出△PAB的“旋补中线”长是
答案解析部分
1.【答案】B
【知识点】几何体的展开图
【解析】【解答】解:由正方体的表面展开图的“相间、Z端是对面”可知,
“英”与“外”是对面,
“雄”与“少”是对面,
“塞”与“年”是对面,
故答案为:B.
【分析】利用正方体展开图的特征求解即可。
2.【答案】D
【知识点】同底数幂的乘法;同底数幂的除法;合并同类项法则及应用;积的乘方
【解析】【解答】解:A、,故该选项不符合题意;
B、,故该选项不符合题意;
C、,故该选项不符合题意;
D、,故该选项符合题意.
故答案为:D.
【分析】合并同类项法则:同类项的系数相加减,所得的结果作为系数,字母和字母的指数不变,据此判断A;同底数幂相乘,底数不变,指数相加,据此判断B;积的乘方,先将每一项进行乘方,然后将结果相乘,据此判断C;同底数幂相除,底数不变,指数相减,.据此判断D.
3.【答案】C
【知识点】分式的值
【解析】【解答】解:;
.
故答案为:C.
【分析】待求式可变形为+1,然后将已知条件代入进行计算.
4.【答案】C
【知识点】全等三角形的判定与性质;矩形的性质;相似三角形的判定与性质
【解析】【解答】∵E为CD的中点,
∴CE=DE,
在矩形ABCD中,AD∥BC,
∴∠DAE=∠CFE,
在△ADE和△CFE中,
,
∴△ADE≌△CFE(AAS),
∴CF=AD=10 ,
∴BF=BC+CF=AD+CF=10 +10 =20 ,
∵tan∠EFC= ,
∴AB=20 × =10,
在Rt△ABF中,AF= =30,
∵AD∥BC,
∴△ADH∽△FBH,
∴ ,
∴AH= AF= ×30=10.
故答案为:C.
【分析】根据线段中点的定义可得CE=DE,根据矩形的对边平行可得AD∥BC,再根据两直线平行,内错角相等可得∠DAE=∠CFE,然后利用“角角边”证明△ADE和△CFE全等,根据全等三角形对应边相等可得CF=AD,再求出BF,然后利用tan∠EFC求出AB,再利用勾股定理列式求出AF,再求出△ADH和△FBH相似,根据相似三角形对应边成比例求出 ,再求解即可.
5.【答案】B
【知识点】直角三角形全等的判定(HL);角平分线的性质;相似三角形的判定与性质;角平分线的定义
【解析】【解答】解:过点E作EF⊥BC于点F,
∵梯形ABCD,AB∥CD,∠A=90°,
∴∠A+∠D=90°,∠DCB+∠ABC=180°,
∴∠D=90°,
∴DE⊥CD,EA⊥AB
∵CE平分∠BCD,BE平分∠ABC ,
∴DE=EF=EA,∠DCB=2∠ECB,∠ABC=2∠EBC,
∴∠ECB+∠EBC=90°,
∴∠CEB=90°;
在Rt△CDE和Rt△CFE中
∴Rt△CDE≌Rt△CFE(HL)
∴CD=CF,
同理可证AB=BF,
∵∠DEC+∠DCE=90°,∠DEC+∠AEB=90°,
∴∠DCE=∠AEB,
∵∠D=∠A=90°,
∴△CDE∽△EAB,
∴,故③正确,①②错误;
∵∠CFE=∠CBE=90°,∠ECF=∠ECB,
∴△ECF∽△BCE,
∴
∴CE2=CD×BC,故④正确;
同理可证△BEF∽△BCE,
∴BE2=BF×BC=AE×BC,故⑤正确;
∴正确结论的序号为③④⑤,一共3个.
故答案为:B
【分析】过点E作EF⊥BC于点F,利用梯形的性质和平行线的性质可证得∠A+∠D=90°,∠DCB+∠ABC=180°,利用角平分线的性质可证得DE=EF=EA,∠DCB=2∠ECB,∠ABC=2∠EBC,从而可推出∠CEB=90°;利用HL证明Rt△CDE≌Rt△CFE,利用全等三角形的性质可得到CD=CF,同理可知AB=BF;再利用有两组对应角分别相等的两三角形相似可证得△CDE∽△EAB,利用相似三角形的对应边成比例,可对①②③作出判断;同理可证得△ECF∽△BCE,利用相似三角形的对应边成比例,可证得 CE2=CD×BC,可对④作出判断;同理可证得BE2=AE×BC,可对⑤作出判断;综上所述可得到正确结论的个数.
6.【答案】A
【知识点】二次函数图象与系数的关系;二次函数y=ax^2+bx+c的性质
【解析】【解答】解:由抛物线可知:,,
对称轴,
,
,故正确;
由对称轴可知:,
,
时,,
,
,故正确;
关于的对称点为,
时,,故正确;
当时,的最小值为,
时,,
,
即,故错误;
抛物线与轴有两个交点,
,
即,
,故正确;
故选:.
【分析】利用二次函数的图象与系数的关系可得a、b、c的正负,再利用二次函数的性质逐项判断即可。
7.【答案】A,B,D
【知识点】勾股定理;垂径定理;圆心角、弧、弦的关系;圆周角定理;三角形全等的判定(ASA)
【解析】【解答】解:∵D是的中点,
∴,
∴,故A符合题意;
∵为直径,
∴,
∴,
∵C是半圆弧的中点,
∴,
∵,
∴,
∴,
∵,
∴,
∴,故B符合题意;
延长,与的延长线交于点E,如图,
∵为直径,
∴,
∵,,
∴,
∴,
∴,
∵,,
∴,故C不符合题意;
连接,
∵,,
∴,
∵,
∴,
∴,故D符合题意.
故答案为:ABD.
【分析】A、根据同圆中等弧所对的圆周角相等即可判断;
B、由AB为直径可得∠ACB=90°,由点C为半圆弧的中点可得AC=BC,根据等腰三角形的性质可得∠BOC=90°,利用余角的性质可得,即可判断;
C、延长,与的延长线交于点E,证明,可得,即得,再根据斜边大于直角边可得BC=AC<AE,即可判断;
D、连接AG,由垂直平分线的性质可得AG=BG,由勾股定理可得,据此即可判断.
8.【答案】a≤2
【知识点】一元二次方程根的判别式及应用
【解析】【解答】解:由题意,得Δ=42-4×2a≥0,
解得a≤2.
故答案为:a≤2.
【分析】一元二次方程ax2+bx+c=0(a≠0),有两个实数根的条件是△=b2-4ac≥0,依此列式计算即可.
9.【答案】
【知识点】比例线段
【解析】【解答】解:a,b,c,d是比例线段,
故答案为:.
【分析】根据比例线段的概念可得,然后将a、b、c的值代入计算可得d的值.
10.【答案】(1,3)
【知识点】坐标与图形变化﹣平移
【解析】【解答】解:∵顶点A(-3,4)的对应点是A1(2,5),
又
∴平移至的规律为:将向右平移5个单位,再向上平移1个单位即可得到
∵B(-4,2)
∴的坐标是(-4+5,2+1),即(1,3)
故答案为:(1,3)
【分析】利用点坐标平移的特征:左减右加,上加下减求解即可。
11.【答案】
【知识点】弧长的计算
【解析】【解答】解:由题意知:∠AOB=360°÷3=120°,半径为1m,
∴的长==,
故答案为:
【分析】根据弧长公式进行解答即可.
12.【答案】30
【知识点】等腰三角形的性质;正方形的性质;数学思想
【解析】【解答】解:如图,连接OR,PR,EG,FH,AC,BD,ED,DG,GB,BE,CH,AH,AF,FC,DH,CG,BF,AE.
由题意,图中有两个正方形:正方形AHCF,正方形DEBG,由此可得16个45°角,
图中有等腰直角三角形三个,△OMH,△PGM,△ORP,由此可得6个45°角,
图中∠DHG=45°,这样的角有8个,
所以一共有16+6+8=30(个),
故答案为30.
【分析】如图,连接相关线段后,找出图中的正方形、等腰直角三角形和与∠DHG一类的角,利用正方形的性质和等腰直角三角形的性质一一判断即可.
13.【答案】解:
.
【知识点】特殊角的三角函数值
【解析】【分析】先利用特殊角的三角函数值、绝对值、0指数幂和负指数幂的性质化简,再计算即可。
14.【答案】(1)解:
(2)解:解不等式①,得 x≤2,
解不等式②,得 ,
因此,原不等式组的解集为 ,
【知识点】分式的混合运算;解一元一次不等式组
【解析】【分析】(1)根据分式的混合运算化简即可;
(2)根据解不等式组的方法进行计算求解即可。
15.【答案】解:
【知识点】实数的运算
【解析】【分析】根据有理数的乘方法则、0次幂的运算法则以及绝对值的性质可得原式=1--1+-1,然后根据有理数的减法法则以及二次根式的加法法则进行计算.
16.【答案】解: ,
方程两边乘 得: ,
解得: ,
检验:当 时, .
所以原方程的解为
【知识点】分式的通分;分式方程的解及检验;解分式方程
【解析】【分析】解分式方程,先分母通分,然后合并同类项,再移项。转化为整式方程的求解。
17.【答案】解:由已知等式得 ,显然 均不为0,∴ =0或 若 ,则 .又 为整数,可求得 或 ∴ 或 ∴, 的值为0或±1.
【知识点】代数式求值;分式的加减法
【解析】【分析】首先根据异分母分式的加法法则将原式变形为,根据分式有意义的条件知 x , y 均不为0,从而得出 x + y =0或 3 x y = 2 ( x y ),由3 x y = 2 ( x y )通过配方可以得到( 3 x + 2 ) ( 3 y 2 ) = 4 ,根据x,y都是整数,从而得出;从而得出x + y = 1 或 x + y = 1 ,综上所述,从而得出答案。
18.【答案】解:原式
,
解不等式组 得 ,
则不等式组的整数解为3,
当 时,原式 .
【知识点】分式的混合运算;解一元一次不等式组
【解析】【分析】根据分式的混合运算可化解题目中的式子,再解出题中的不等式组,根据x为整数可得出x的值,从而代入可求出答案
19.【答案】(1)第二步
(2)解:(棵),
这260名学生共植树约为(棵).
【知识点】平均数及其计算
【解析】【分析】本题考查平均数的计算。题目中,总的植树量是每种类型数量乘以人数,再求和之后,除以总人数,得出每人植树量的平均数,仔细审题,正确理解题意是关键。
20.【答案】证明:∵AD∥BC,
∴∠A=∠C,∠D=∠B
在△EAD和△ECB中,
∴△EAD≌△ECB(ASA)
∴EA=EC
即E为AC的中点.
【知识点】三角形全等的判定(ASA)
【解析】【分析】利用“ASA”证明△EAD≌△ECB可得EA=EC,即可得到点E为AC的中点。
21.【答案】证明:∵四边形ABCD是正方形,
∴AB=BC=CD=AD,∠A=∠C=90°,
∵△BEF是等边三角形,
∴BE=BF,
在Rt△ABF和Rt△CBE中,
,
∴Rt△ABF≌Rt△CBE(HL),
∴AF=CE,
∴CD-CE=AD-AF,
∴DE=DF.
【知识点】直角三角形全等的判定(HL);等边三角形的性质;正方形的性质
【解析】【分析】由正方形的性质可得AB=BC=CD=AD,∠A=∠C=90°,由等边三角形的性质可得BE=BF,证明Rt△ABF≌Rt△CBE,得到AF=CE,据此证明.
22.【答案】证明:∵DE∥BC,
∴;
∵DF∥AC ,
∴;
∴
【知识点】平行线分线段成比例
【解析】【分析】根据平行于三角形一边的直线,截其他两边(或两边延长线)所得的对应线段成比例可得;;即可证明.
23.【答案】(1)证明:∵OA=OC,
∴∠A=∠ACO.
又∵∠COB=2∠A,∠COB=2∠PCB,
∴∠A=∠ACO=∠PCB.
又∵AB是⊙O的直径,
∴∠ACO+∠OCB=90°.
∴∠PCB+∠OCB=90°.
即OC⊥CP,
∵OC是⊙O的半径.
∴PC是⊙O的切线.
(2)证明:∵AC=PC,
∴∠A=∠P,
∴∠A=∠ACO=∠PCB=∠P.
又∵∠COB=∠A+∠ACO,∠CBO=∠P+∠PCB,
∴∠COB=∠CBO,
∴BC=OC.
∴BC= AB.
(3)解:连接MA,MB,
∵点M是 的中点,
∴ = ,
∴∠ACM=∠BCM.
∵∠ACM=∠ABM,
∴∠BCM=∠ABM.
∵∠BMN=∠BMC,
∴△MBN∽△MCB.
∴ ,
∴BM2=MN MC.
又∵AB是⊙O的直径, = ,
∴∠AMB=90°,AM=BM.
∵AB=4,
∴BM=2 .
∴MN MC=BM2=8.
【知识点】圆周角定理;切线的判定与性质
【解析】【分析】(1)由半径OA=OC,可得等边对等角∠A=∠ACO,则∠COB=2∠A,已知∠COB=2∠PCB,∠A=∠ACO=∠PCB.由直径所对的圆周角是直角可得∠ACO+∠OCB=90°.从而转换得到∠PCB+∠OCB=90°即可证得;(2)“等角对等边”与“等边对等角”相互运用可证OC=BC;(3)连接MA,MB,先证明△MBN∽△MCB.则 ,即BM2=MN MC.由AB是⊙O的直径, = ,AB=4,解出BM,从而可解得MN MC.
24.【答案】解:(Ⅰ)当a=b=1,c=﹣1时,抛物线为y=3x2+2x﹣1,方程3x2+2x﹣1=0的两个根为x1=﹣1, .∴该抛物线与x轴公共点的坐标是(﹣1,0)和( ,0);(Ⅱ)当a=b=1时,抛物线为y=3x2+2x+c,且与x轴有公共点.对于方程3x2+2x+c=0,判别式△=4﹣12c≥0,有c≤ .①当 时,由方程3x2+2x+ =0,解得x1=x2=﹣ .此时抛物线为y=3x2+2x+ 与x轴只有一个公共点(﹣ ,0);②当 时,x1=﹣1时,y1=3﹣2+c=1+c;x2=1时,y2=3+2+c=5+c.由已知﹣1<x<1时,该抛物线与x轴有且只有一个公共点,考虑其对称轴为 ,应有 即 ,解得﹣5<c≤﹣1.综上, 或﹣5<c≤﹣1.(6分)(Ⅲ)对于二次函数y=3ax2+2bx+c,由已知x1=0时,y1=c>0;x2=1时,y2=3a+2b+c>0,又∵a+b+c=0,∴3a+2b+c=(a+b+c)+2a+b=2a+b.∴2a+b>0.∵b=﹣a﹣c,∴2a﹣a﹣c>0,即a﹣c>0.∴a>c>0.(7分)∵关于x的一元二次方程3ax2+2bx+c=0的判别式△=4b2﹣12ac=4(a+c)2﹣12ac=4[(a﹣c)2+ac]>0,∴抛物线y=3ax2+2bx+c与x轴有两个公共点,顶点在x轴下方.又该抛物线的对称轴 ,由a+b+c=0,c>0,2a+b>0,得﹣2a<b<﹣a,∴ .又由已知x1=0时,y1>0;x2=1时,y2>0,观察图象, 可知在0<x<1范围内,该抛物线与x轴有两个公共点.
【知识点】二次函数图象与坐标轴的交点问题
【解析】【分析】(Ⅰ)把a,b,c的值代入可得抛物线的解析式,然后令y=0可得到关于x的方程,然后求得方程的两根,从而可得到抛物线与x轴交点坐标;
(Ⅱ)把a,b代入可得到抛物线的解析式,然后可求得抛物线的对称轴为x=-,然后再分为△=0和△>0两种情况求解即可;
(Ⅲ)抛物线y=3ax2+2bx+c与x轴公共点的个数就是一元二次方程3ax2+2bx+c=0的实数根的个数,接下来,判断出方程3ax2+2bx+c=0根的判别式的符号,依据判别式的符号得出相应的结论.
25.【答案】解:①如图所示:点C1的坐标(5,﹣3);
②如图所示,点C2的坐标(﹣5,3).
【知识点】作图﹣轴对称;作图﹣旋转
【解析】【分析】①利用关于x轴对称的点的坐标特点:横坐标不变,纵坐标互为相反数,据此画出△A1B1C1,写出点C1的坐标;②利用关于原点对称的点的坐标特点:横纵坐标都互为相反数,可得到点A2、B2、C2,再画出△A2B2C2,写出点C2的坐标.
26.【答案】(1)4;解:②大致图像如图, 交点坐标为: 或
(2)是;解:②∵ , ∴ . 同理 , ∴ , , ∴ . ∵ ,∴ , . ∵ ,∴ , ∴ 或
【知识点】二次函数图象上点的坐标特征;二次函数y=ax^2+bx+c的图象;二次函数y=ax^2+bx+c的性质
【解析】【解答】解:(1)①由题意 可得 求得 ;(2)①根据题干所给“窗帘”抛物线的定义 可知 满足定义所以为:是;
【分析】(1)①题干要求 的值,利用题干所给“窗帘”抛物线的定义分析即可求得,②题干要求画出大致图像,并写出交点坐标,采用描点法进行绘制,(2)①题干要求判断它们是否是“窗帘”抛物线,利用题干所给“窗帘”抛物线的定义分析即可求得,
②题干告知 ,要求 的值,分别表示D,E,F三点的坐标,并利用距离坐标公式求知答案.
27.【答案】(1)证明: : : : ,
,
,
∽ ;
(2)解: ∽ ,
,
,
,
的长为10.
【知识点】相似三角形的判定与性质
【解析】【分析】(1)根据已知条件可得,然后结合有两组边对应成比例,且夹角相等的两个三角形相似,进行证明;
(2)直接根据相似三角形对应边成比例进行计算.
28.【答案】(1)解:画出函数的y=(x﹣1)2图象如图所示:
当﹣2≤x≤﹣1时,y的取值范围是4≤y≤9
(2)解:当0≤x≤3时,y的取值范围是0≤y≤4
【知识点】二次函数y=a(x-h)^2+k的图象;二次函数y=a(x-h)^2+k的性质
【解析】【分析】(1)由函数图象得知函数对称轴为x=1, 当﹣2≤x≤﹣1时 ,函数单调递减,求出x=-2和x=-1时y的取值,确定取值区间。
(2)函数对称轴为x=1,故在x=1时,函数y取值最小;在1≤x≤3时,单调递增,即求出x=3时y的取值,即可求出y的取值范围。
29.【答案】(1)解:设抛物线y=x2+2x的顶点为G,
∵y=x2+2x=(x+1)2﹣1,
∴G(﹣1,﹣1),
∵将C1绕着点O旋转180°,得到C2,
∴点G与点E关于原点O对称,
∴E(1,1);
(2)4
【知识点】旋转的性质;关于原点对称的点的坐标特征;二次函数y=ax^2+bx+c与二次函数y=a(x-h)^2+k的转化
【解析】【解答】(2)设C3的最低点为F,
令y=0,则x2+2x=0,
解得:x=0或x=﹣2,
∴A(﹣2,0),
由题意:点A与点B关于原点O对称,
∴B(2,0),
∵将C2绕着点B旋转180°得到C3,
∴点E与点F关于原点O对称,
∴F(3,﹣1),
过点G作GH⊥OA于点H,过点F作FK⊥BD于点K,过点E作EM⊥OB于点M,如图,
∵G(﹣1,﹣1),F(3,﹣1),
∴GF∥HK,GH=FK=1,
∵GH⊥OA,FK⊥BD,
∴四边形GHKF为矩形.
∵G(﹣1,﹣1),F(3,﹣1),
∴HO=1,OK=3,
∴HK=OH+OK=4,
根据旋转不变性可得:S阴影部分=S矩形GHKF,
∴S阴影部分=HK HG=4×1=4,
故答案为:4.
【分析】(1)先求出 G(﹣1,﹣1), 再求出 点G与点E关于原点O对称, 最后求解即可;
(2)先求出B(2,0),再求出HK=OH+OK=4,最后求解即可。
30.【答案】(1)解:设每台A型机器人每天搬运货物吨,则每台型机器人每天搬运货物吨,
由题意得:,
解得:,
当时,,
是分式方程的根,
(吨),
答:每台A型机器人每天搬运货物90吨,则每台型机器人每天搬运货物100吨;
(2)解:设购买A型机器人台,购买总金额为万元,
由题意得:,
解得:,
;
,
随的增大而减小,
当时,最小,此时,
购买A型机器人17台,型机器人13台时,购买总金额最低是46.4万元.
【知识点】分式方程的实际应用;一次函数的实际应用
【解析】【分析】(1)设每台A型机器人每天搬运货物吨,则每台型机器人每天搬运货物吨,根据“ A型机器人每天搬运540吨货物与型机器人每天搬运600吨货物所需台数相同”,列出方程并解之即可;
(2)设购买A型机器人台,购买总金额为万元,根据“ 每天搬运的货物不低于2830吨,购买金额不超过48万元 ”列出不等式组,求出m的范围,根据总金额=A型机器费用+B型机器费用,列出w关于m的函数解析式,再利用一次函数的性质求解即可.
31.【答案】(1)解:∵抛物线y=﹣x2+bx+c与x轴分别交于A(﹣1,0),B(5,0)两点,
∴,解得,
∴抛物线解析式为y=﹣x2+4x+5;
(2)解:∵AD=5,且OA=1,
∴OD=6,且CD=8,
∴C(﹣6,8),
设平移后的点C的对应点为C′,则C′点的纵坐标为8,
代入抛物线解析式可得8=﹣x2+4x+5,解得x=1或x=3,
∴C′点的坐标为(1,8)或(3,8),
∵C(﹣6,8),
∴当点C落在抛物线上时,向右平移了7或9个单位,
∴m的值为7或9;
(3)解:∵y=﹣x2+4x+5=﹣(x﹣2)2+9,
∴抛物线对称轴为x=2,
∴可设P(2,t),
由(2)可知E点坐标为(1,8),
①当BE为平行四边形的边时,连接BE交对称轴于点M,过E作EF⊥x轴于点F,当BE为平行四边形的边时,过Q作对称轴的垂线,垂足为N,如图,
则∠BEF=∠BMP=∠QPN,
在△PQN和△EFB中
∴△PQN≌△EFB(AAS),
∴NQ=BF=OB﹣OF=5﹣1=4,
设Q(x,y),则QN=|x﹣2|,
∴|x﹣2|=4,解得x=﹣2或x=6,
当x=﹣2或x=6时,代入抛物线解析式可求得y=﹣7,
∴Q点坐标为(﹣2,﹣7)或(6,﹣7);
②当BE为对角线时,
∵B(5,0),E(1,8),
∴线段BE的中点坐标为(3,4),则线段PQ的中点坐标为(3,4),
设Q(x,y),且P(2,t),
∴x+2=3×2,解得x=4,把x=4代入抛物线解析式可求得y=5,
∴Q(4,5);
综上可知Q点的坐标为(﹣2,﹣7)或(6,﹣7)或(4,5).
【知识点】待定系数法求二次函数解析式;平行四边形的性质;二次函数图象上点的坐标特征;用坐标表示平移;三角形全等的判定(AAS)
【解析】【分析】(1)将点A、B的坐标代入 y=-x2+bx+c 可得b、c,据此可得抛物线的解析式;
(2)易得C(﹣6,8),设平移后的点C的对应点为C′,则C′点的纵坐标为8,将y=8代入抛物线解析式中求出x,可得C′点的坐标,然后利用点的平移规律进行解答;
(3)根据抛物线的解析式可得对称轴为x=2,设P(2,t),由(2)可知E点坐标为(1,8),①当BE为平行四边形的边时,连接BE交对称轴于点M,过E作EF⊥x轴于点F,过Q作对称轴的垂线,垂足为N,则∠BEF=∠BMP=∠QPN,证明△PQN≌△EFB,得到NQ=BF=OB-OF=4,设Q(x,y),则QN=|x-2|,据此得x,然后代入抛物线解析式中求出y,进而得点Q的坐标;②当BE为对角线时,易知线段BE的中点坐标为(3,4),线段PQ的中点坐标为(3,4),设Q(x,y),且P(2,t),则有x+2=3×2,求出x,然后代入抛物线解析式中求出y,进而可得点Q的坐标.
32.【答案】(1)45°;3
(2)解:如答图1所示,连接CD并延长,交x轴于点F.
在△BCD与△AFD中,
∴△BCD≌△AFD(ASA).
∴CD=FD,即点D为Rt△COF斜边CF的中点,
∴OD= CF=CD.
又由折叠可知,OD=OC,
∴OD=OC=CD,
∴△OCD为等边三角形,∠COD=60°,
∴θ= ∠COD=30°
(3)解:经过FZ[45°,a]操作,点B落在点E处,则点D落在x轴上,AB⊥直线l,
如答图2所示:
若点E在四边形0ABC的边AB上,
由折叠可知,OD=OC=3,DE=BC=2.
∵AB⊥直线l,θ=45°,
∴△ADE为等腰直角三角形,
∴AD=DE=2,
∴OA=OD+AD=3+2=5,
∴a=5;
由答图2可知,当0<a<5时,点E落在四边形0ABC的外部
(4)FZ[30°,2+ ],FZ[60°,2+ ].
如答图3、答图4所示.
【知识点】全等三角形的判定与性质;等边三角形的判定与性质;含30°角的直角三角形;等腰直角三角形;直角三角形斜边上的中线
【解析】【解答】解:【理解】
若点D与点A重合,由折叠性质可知,OA=OC=3,θ= ∠AOC=45°,
∴FZ[45°,3].
【分析】【理解】由折叠性质可以直接得出.【尝试】(2)如答图1所示,若点D恰为AB的中点,连接CD并延长交x轴于点F.证明△BCD≌△AFD,进而得到△OCD为等边三角形,则θ=30°;(3)如答图2所示,若点E在四边形0ABC的边AB上,则△ADE为等腰直角三角形,由此求出a=OA=OD+OA=5;由答图2进一步得到,当0<a<5时,点E落在四边形0ABC的外部.【探究】满足条件的图形有两种,如答图3、答图4所示,
33.【答案】(1);4
(2)解:结论:AD= BC.
理由:如图1中,延长AD到M,使得AD=DM,连接B′M,C′M
∵B′D=DC′,AD=DM,
∴四边形AC′MB′是平行四边形,
∴AC′=B′M=AC,
∵∠BAC+∠B′AC′=180°,∠B′AC′+∠AB′M=180°,
∴∠BAC=∠MB′A,∵AB=AB′,
∴△BAC≌△AB′M,
∴BC=AM,
∴AD= BC.
(3)
【知识点】旋转的性质;三角形的综合
【解析】【解答】解:(1)①如图2中,
∵△ABC是等边三角形,
∴AB=BC=AC=AB′=AC′,
∵DB′=DC′,
∴AD⊥B′C′,
∵∠BAC=60°,∠BAC+∠B′AC′=180°,
∴∠B′AC′=120°,
∴∠B′=∠C′=30°,
∴AD= AB’= BC,
故答案为 :;
②如图3中,
∵∠BAC=90°,∠BAC+∠B′AC′=180°,
∴∠B′AC′=∠BAC=90°,
∵AB=AB′,AC=AC′,
∴△BAC≌△B′AC′,
∴BC=B′C′,
∵B′D=DC′,
∴AD= B′C′= BC=4,
故答案为:4;
( 3 ) .
理由:如图4中,延长AD交BC的延长线于M,作BE⊥AD于E,作线段BC的垂直平分线交BE于P,交BC于F,连接PA、PD、PC,作△PCD的中线PN.
连接DF交PC于O.
∵∠ADC=150°,
∴∠MDC=30°,
在Rt△DCM中,∵CD=2 ,∠DCM=90°,∠MDC=30°,
∴CM=2,DM=4,∠M=60°,
在Rt△BEM中,∵∠BEM=90°,BM=14,∠MBE=30°,
∴EM= BM=7,
∴DE=EM-DM=3,
∵AD=6,
∴AE=DE,
∵BE⊥AD,
∴PA=PD,PB=PC,
在Rt△CDF中,∵CD=2 ,CF=6,
∴tan∠CDF= ,
∴∠CDF=60°
∴∠ADF=90°=∠AEB,
∴∠CBE=∠CFD,
∵∠CBE=∠PCF,
∴∠CFD=∠PCF,
∵∠CFD+∠CDF=90°,∠PCF+∠CPF=90°,
∴∠CPF=∠CDF=60°=∠CDF
易证△FCP≌△CFD,
∴CD=PF,∵CD∥PF,
∴四边形CDPF是矩形,
∴∠CDP=90°,
∴∠ADP=∠ADC-∠CDP=60°,
∴△ADP是等边三角形,
∴∠ADP=60°,∵∠BPF=∠CPF=60°,
∴∠BPC=120°,
∴∠APD+∠BPC=180°,
∴△PDC是△PAB的“旋补三角形”,
∵AB=2 .
∴△PAB的“旋补中线”长= AB= .
故答案为: .
【分析】(1)①首先证明△ADB′是含有30°是直角三角形,可得AD= AB′即可解决问题;②首先证明△BAC≌△B′AC′,根据直角三角形斜边中线定理即可解决问题;
(2)结论:AD= BC.如图1中,延长AD到M,使得AD=DM,连接B′M,C′M,首先证明四边形AC′MB′是平行四边形,再证明△BAC≌△AB′M,即可解决问题;
(3)存在.如图4中,延长AD交BC的延长线于M,作BE⊥AD于E,作线段BC的垂直平分线交BE于P,交BC于F,连接PA、PD、PC,作△PCD的中线PN.连接DF交PC于O.想办法证明PA=PD,PB=PC,再证明∠APD+∠BPC=180°,即可得出结论.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
