福建省泉州七中08-09学年高二下学期第二次月考(数学文)
文档属性
| 名称 | 福建省泉州七中08-09学年高二下学期第二次月考(数学文) |

|
|
| 格式 | rar | ||
| 文件大小 | 170.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2009-06-20 17:13:00 | ||
图片预览




文档简介
2008-2009学年第二学期高二年第二次月考考试文科数学试卷
(考试时间为120分钟,满分为150分) 命题人:张丽英 2009年5月
一、选择题(本大题共12小题每小题5分;共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.)
1.已知集合,,则( )
A. B. C. D.
2.复数在复平面内对应的点位于( )
A. 第一象限 B.第二象限 C. 第三象限 D. 第四象限
3.若命题“p或q”是真命题,“p且q”是假命题,则( )
A.命题p和命题q都是假命题 B.命题p和命题q都是真命题
C.命题p和命题“非q”的真值不同 D. 命题p和命题q的真值不同
4.若,则下列不等式正确的是( ) 21世纪教育网
A. B. C. D.
5.已知,则的值是( )
A. B. C. D.
6.幂函数及直线y=x,y=1,x=1将平面直角坐标系的第一 象限分成八个“卦限”:①,②,③,④,⑤,⑥,⑦,⑧(如图所示),那么幂函数的图象经过的“卦限”是( )
A.⑧,③ B.⑦,③
C.⑥,① D.⑤,①
7.下列有关命题的说法正确的是 ( ).
A.命题“若,则”的否命题为:“若,则”.
B.“”是“”的必要不充分条件.21世纪教育网
C.命题“使得”的否定是:“ 均有”.
D.命题“若,则”的逆否命题为真命题.
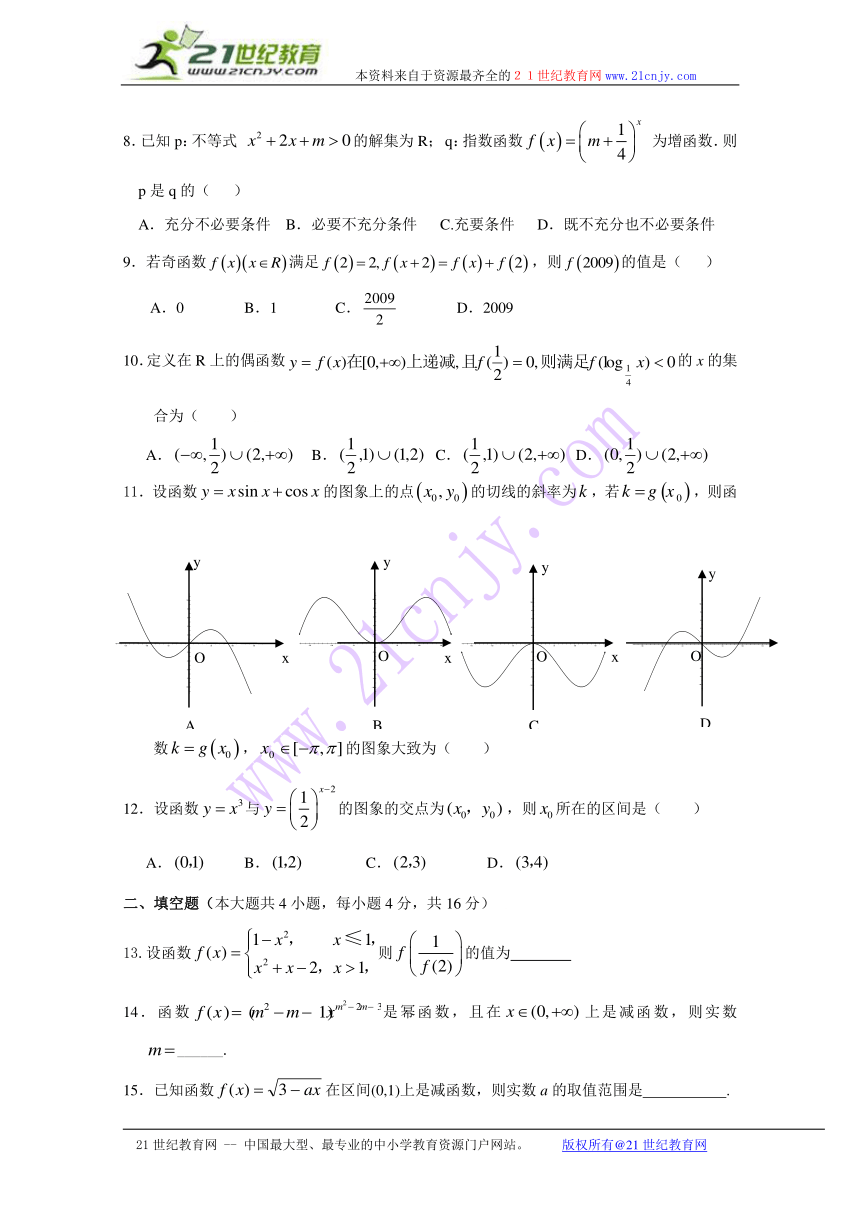
8.已知p:不等式 的解集为R; q:指数函数 为增函数.则p是q的( )
A.充分不必要条件 B.必要不充分条件 C.充要条件 D.既不充分也不必要条件
9.若奇函数满足,则的值是( )
A.0 B.1 C. D.2009
10.定义在R上的偶函数的x的集合为( )21世纪教育网
A. B. C. D.
11.设函数的图象上的点的切线的斜率为,若,则函数,的图象大致为( )
12.设函数与的图象的交点为,则所在的区间是( )
A. B. C. D.
二、填空题(本大题共4小题,每小题4分,共16分)21世纪教育网
13.设函数则的值为
14.函数是幂函数,且在上是减函数,则实数______.
15.已知函数在区间(0,1)上是减函数,则实数a的取值范围是 .
16.如果一个自然数,我们可以把它写成若干个连续自然数之和,则称为自然数的一个“分拆”.如,我们就说“”与“”是的两个“分拆”.请写出自然数30的两个“分拆”:. .
三、解答题(本大题共6小题;共74分.解答应写出文字说明、证明过程或演算步骤.)
17.(满分12分)已知p:,q:,若非p是非q的必要而不充分条件,求实数m的取值范围.21世纪教育网
18.(满分12分)已知函数 21世纪教育网
(1)求证:函数是偶函数;
(2)判断函数分别在区间、上的单调性, 并加以证明;
19.(满分12分)已知函数的定义域为, (1)求M (2)当 时,求 的最小值. 21世纪教育网
20.(满分12分)某自来水厂的蓄水池存有400吨水,水厂每小时可向蓄水池中注水60吨,同时蓄水池又向居民小区不间断供水,小时内供水总量为吨,()
(1)从供水开始到第几小时时,蓄水池中的存水量最少?最少水量是多少吨?
(2)若蓄水池中水量少于80吨时,就会出现供水紧张现象,请问:在一天的24小时内,有几小时出现供水紧张现象。21世纪教育网
21.(满分12分)在平面直角坐标系中,点,点是平面上动点,且成等差数列。21世纪教育网
(1)求动点满足的曲线方程;
(2)设直线与曲线交于两点,试问:当变化时,是否存在直线,使的面积为?若存在,求出直线的方程;若不存在,说明理由。
22.(满分14分)已知函数
(1)若处取得极值,求实数a的值;
(2)在(1)的条件下,若关于x的方程上恰有两个不同的实数根,求实数m的取值范围;21世纪教育网
(3)若存在,使得不等式成立,求实数a的取值范围。
一、选择题
1-3 B B D C D D
A D B D A B
二、填空题
13. 14. 13.
14. 9+10+11 ,4+5+6+7+8 ,6+7+8+9 (选对其中两个即可)
三、解答题(本大题共6小题;共74分.解答应写出文字说明、证明过程或演算步骤.)
17.(满分12分)已知p:,q:,若非p是非q的必要而不充分条件,求实数m的取值范围.
17.由x2-2x+1-m2≤0,得1-m≤x≤1+m(m>0),…………………….3分
由得-2≤即-2≤x≤10.………………..6分
则非p:x<-2或x>10. ………………………………………….7分
非q:x>1+m或x<1-m(m>0).………………………………….8分
若非p是非q的必要不充分条件,则:
∴m≥9 ………………………………………………………………….12分
18.(满分12分)已知函数
(1)求证:函数是偶函数;
(2)判断函数分别在区间、上的单调性, 并加以证明;
18.解:(1) 当时,,
则
∴ 当时, , ………………………….3分
则,
∴
综上所述, 对于, 都有,
∴ 函数是偶函数。………………………………………………….6分
(2)当时,
设, 则.…………………8分
当时, ;
当时, ,
∴ 函数在上是减函数, 函数在上是增函数。….12分
19.(满分12分)已知函数的定义域为, (1)求M ,(2)当 时,求 的最小值. 解 (1) (…………4分)
(2)=
又,,(…………………6分)
①若,即时,==,(…………8分)
②若,即时,
所以当即时,=(………………11分)
……………………………………………….12分
20.(满分12分)某自来水厂的蓄水池存有400吨水,水厂每小时可向蓄水池中注水60吨,同时蓄水池又向居民小区不间断供水,小时内供水总量为吨,()
(1)从供水开始到第几小时时,蓄水池中的存水量最少?最少水量是多少吨?
(2)若蓄水池中水量少于80吨时,就会出现供水紧张现象,请问:在一天的24小时内,有几小时出现供水紧张现象。
解:(1)设小时后蓄水池中的水量为吨,
则; ————————————————————3分
令=;则,即;——5分
∴当,即时,,
即从供水开始到第6小时时,蓄水池水量最少,只有40吨。————————7分
(2)依题意,得 ——————————10分
解得,,即,;
即由,所以每天约有8小时供水紧张。——-———————————12分
21.(满分12分)在平面直角坐标系中,点,点是平面上动点,且成等差数列。
(1)求动点满足的曲线方程;
(2)设直线与曲线交于两点,试问:当变化时,是否存在直线,使的面积为?若存在,求出直线的方程;若不存在,说明理由。
21.解:(I)由题意知,…………………..2分
由椭圆定义知,动点满足的曲线方程是:…………………4分
(II)由方程组
……………………………………………….7分
的面积………10分
不存在直线满足题意……………….12分
22.(满分14分)已知函数
(1)若处取得极值,求实数a的值;
(2)在(1)的条件下,若关于x的方程上恰有两个不同的实数根,求实数m的取值范围;
(3)若存在,使得不等式成立,求实数a的取值范围。
22.解:(1)………………….1分
由题意得,……………….2分
经检验满足条件。…………………………………….3分
(2)由(1)知
令(舍去)………………4分
当x变化时,的变化情况如下表:
x
-1
(-1,0)
0
(0,1)
1
-
0
+
-1
↘
-4
↗
-3
…………………………6分
∵关于x的方程上恰有两个不同的实数根,
……………………8分
(3)由题意得,
………………9分
①若单调递减。
∴当
②当a>0时随x的变化情况如下表:
x
(,+)
+
0
—
↗
↘
…………………………12分
由
综上得a>3.…………………………14分
(考试时间为120分钟,满分为150分) 命题人:张丽英 2009年5月
一、选择题(本大题共12小题每小题5分;共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.)
1.已知集合,,则( )
A. B. C. D.
2.复数在复平面内对应的点位于( )
A. 第一象限 B.第二象限 C. 第三象限 D. 第四象限
3.若命题“p或q”是真命题,“p且q”是假命题,则( )
A.命题p和命题q都是假命题 B.命题p和命题q都是真命题
C.命题p和命题“非q”的真值不同 D. 命题p和命题q的真值不同
4.若,则下列不等式正确的是( ) 21世纪教育网
A. B. C. D.
5.已知,则的值是( )
A. B. C. D.
6.幂函数及直线y=x,y=1,x=1将平面直角坐标系的第一 象限分成八个“卦限”:①,②,③,④,⑤,⑥,⑦,⑧(如图所示),那么幂函数的图象经过的“卦限”是( )
A.⑧,③ B.⑦,③
C.⑥,① D.⑤,①
7.下列有关命题的说法正确的是 ( ).
A.命题“若,则”的否命题为:“若,则”.
B.“”是“”的必要不充分条件.21世纪教育网
C.命题“使得”的否定是:“ 均有”.
D.命题“若,则”的逆否命题为真命题.
8.已知p:不等式 的解集为R; q:指数函数 为增函数.则p是q的( )
A.充分不必要条件 B.必要不充分条件 C.充要条件 D.既不充分也不必要条件
9.若奇函数满足,则的值是( )
A.0 B.1 C. D.2009
10.定义在R上的偶函数的x的集合为( )21世纪教育网
A. B. C. D.
11.设函数的图象上的点的切线的斜率为,若,则函数,的图象大致为( )
12.设函数与的图象的交点为,则所在的区间是( )
A. B. C. D.
二、填空题(本大题共4小题,每小题4分,共16分)21世纪教育网
13.设函数则的值为
14.函数是幂函数,且在上是减函数,则实数______.
15.已知函数在区间(0,1)上是减函数,则实数a的取值范围是 .
16.如果一个自然数,我们可以把它写成若干个连续自然数之和,则称为自然数的一个“分拆”.如,我们就说“”与“”是的两个“分拆”.请写出自然数30的两个“分拆”:. .
三、解答题(本大题共6小题;共74分.解答应写出文字说明、证明过程或演算步骤.)
17.(满分12分)已知p:,q:,若非p是非q的必要而不充分条件,求实数m的取值范围.21世纪教育网
18.(满分12分)已知函数 21世纪教育网
(1)求证:函数是偶函数;
(2)判断函数分别在区间、上的单调性, 并加以证明;
19.(满分12分)已知函数的定义域为, (1)求M (2)当 时,求 的最小值. 21世纪教育网
20.(满分12分)某自来水厂的蓄水池存有400吨水,水厂每小时可向蓄水池中注水60吨,同时蓄水池又向居民小区不间断供水,小时内供水总量为吨,()
(1)从供水开始到第几小时时,蓄水池中的存水量最少?最少水量是多少吨?
(2)若蓄水池中水量少于80吨时,就会出现供水紧张现象,请问:在一天的24小时内,有几小时出现供水紧张现象。21世纪教育网
21.(满分12分)在平面直角坐标系中,点,点是平面上动点,且成等差数列。21世纪教育网
(1)求动点满足的曲线方程;
(2)设直线与曲线交于两点,试问:当变化时,是否存在直线,使的面积为?若存在,求出直线的方程;若不存在,说明理由。
22.(满分14分)已知函数
(1)若处取得极值,求实数a的值;
(2)在(1)的条件下,若关于x的方程上恰有两个不同的实数根,求实数m的取值范围;21世纪教育网
(3)若存在,使得不等式成立,求实数a的取值范围。
一、选择题
1-3 B B D C D D
A D B D A B
二、填空题
13. 14. 13.
14. 9+10+11 ,4+5+6+7+8 ,6+7+8+9 (选对其中两个即可)
三、解答题(本大题共6小题;共74分.解答应写出文字说明、证明过程或演算步骤.)
17.(满分12分)已知p:,q:,若非p是非q的必要而不充分条件,求实数m的取值范围.
17.由x2-2x+1-m2≤0,得1-m≤x≤1+m(m>0),…………………….3分
由得-2≤即-2≤x≤10.………………..6分
则非p:x<-2或x>10. ………………………………………….7分
非q:x>1+m或x<1-m(m>0).………………………………….8分
若非p是非q的必要不充分条件,则:
∴m≥9 ………………………………………………………………….12分
18.(满分12分)已知函数
(1)求证:函数是偶函数;
(2)判断函数分别在区间、上的单调性, 并加以证明;
18.解:(1) 当时,,
则
∴ 当时, , ………………………….3分
则,
∴
综上所述, 对于, 都有,
∴ 函数是偶函数。………………………………………………….6分
(2)当时,
设, 则.…………………8分
当时, ;
当时, ,
∴ 函数在上是减函数, 函数在上是增函数。….12分
19.(满分12分)已知函数的定义域为, (1)求M ,(2)当 时,求 的最小值. 解 (1) (…………4分)
(2)=
又,,(…………………6分)
①若,即时,==,(…………8分)
②若,即时,
所以当即时,=(………………11分)
……………………………………………….12分
20.(满分12分)某自来水厂的蓄水池存有400吨水,水厂每小时可向蓄水池中注水60吨,同时蓄水池又向居民小区不间断供水,小时内供水总量为吨,()
(1)从供水开始到第几小时时,蓄水池中的存水量最少?最少水量是多少吨?
(2)若蓄水池中水量少于80吨时,就会出现供水紧张现象,请问:在一天的24小时内,有几小时出现供水紧张现象。
解:(1)设小时后蓄水池中的水量为吨,
则; ————————————————————3分
令=;则,即;——5分
∴当,即时,,
即从供水开始到第6小时时,蓄水池水量最少,只有40吨。————————7分
(2)依题意,得 ——————————10分
解得,,即,;
即由,所以每天约有8小时供水紧张。——-———————————12分
21.(满分12分)在平面直角坐标系中,点,点是平面上动点,且成等差数列。
(1)求动点满足的曲线方程;
(2)设直线与曲线交于两点,试问:当变化时,是否存在直线,使的面积为?若存在,求出直线的方程;若不存在,说明理由。
21.解:(I)由题意知,…………………..2分
由椭圆定义知,动点满足的曲线方程是:…………………4分
(II)由方程组
……………………………………………….7分
的面积………10分
不存在直线满足题意……………….12分
22.(满分14分)已知函数
(1)若处取得极值,求实数a的值;
(2)在(1)的条件下,若关于x的方程上恰有两个不同的实数根,求实数m的取值范围;
(3)若存在,使得不等式成立,求实数a的取值范围。
22.解:(1)………………….1分
由题意得,……………….2分
经检验满足条件。…………………………………….3分
(2)由(1)知
令(舍去)………………4分
当x变化时,的变化情况如下表:
x
-1
(-1,0)
0
(0,1)
1
-
0
+
-1
↘
-4
↗
-3
…………………………6分
∵关于x的方程上恰有两个不同的实数根,
……………………8分
(3)由题意得,
………………9分
①若单调递减。
∴当
②当a>0时随x的变化情况如下表:
x
(,+)
+
0
—
↗
↘
…………………………12分
由
综上得a>3.…………………………14分
同课章节目录
