初中数学(通用版)九年级历年中考常考知识点综合练习题02(精华)
文档属性
| 名称 | 初中数学(通用版)九年级历年中考常考知识点综合练习题02(精华) |  | |
| 格式 | docx | ||
| 文件大小 | 4.0MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-04-18 09:21:14 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
初中数学(通用版)九年级历年中考常考知识点综合练习题02(精华)
一、单选题
1.直角三角形的两条直角边的长分别为6和8,则斜边长为( )
A.10 B.5 C.4 D.3
2.关于x的一元二次方程有实数根,则m的取值范围是( )
A. B. C. D.
3.为增强班级凝聚力,吴老师组织开展了一次主题班会.班会上,他设计了一个如图的飞镖靶盘,靶盘由两个同心圆构成,小圆半径为,大圆半径为,每个扇形的圆心角为60度.如果用飞镖击中靶盘每一处是等可能的,那么小全同学任意投掷飞镖1次(击中边界或没有击中靶盘,则重投1次),投中“免一次作业”的概率是( )
A. B. C. D.
4.已知,则的值是( )
A.3 B.-3 C. D.-
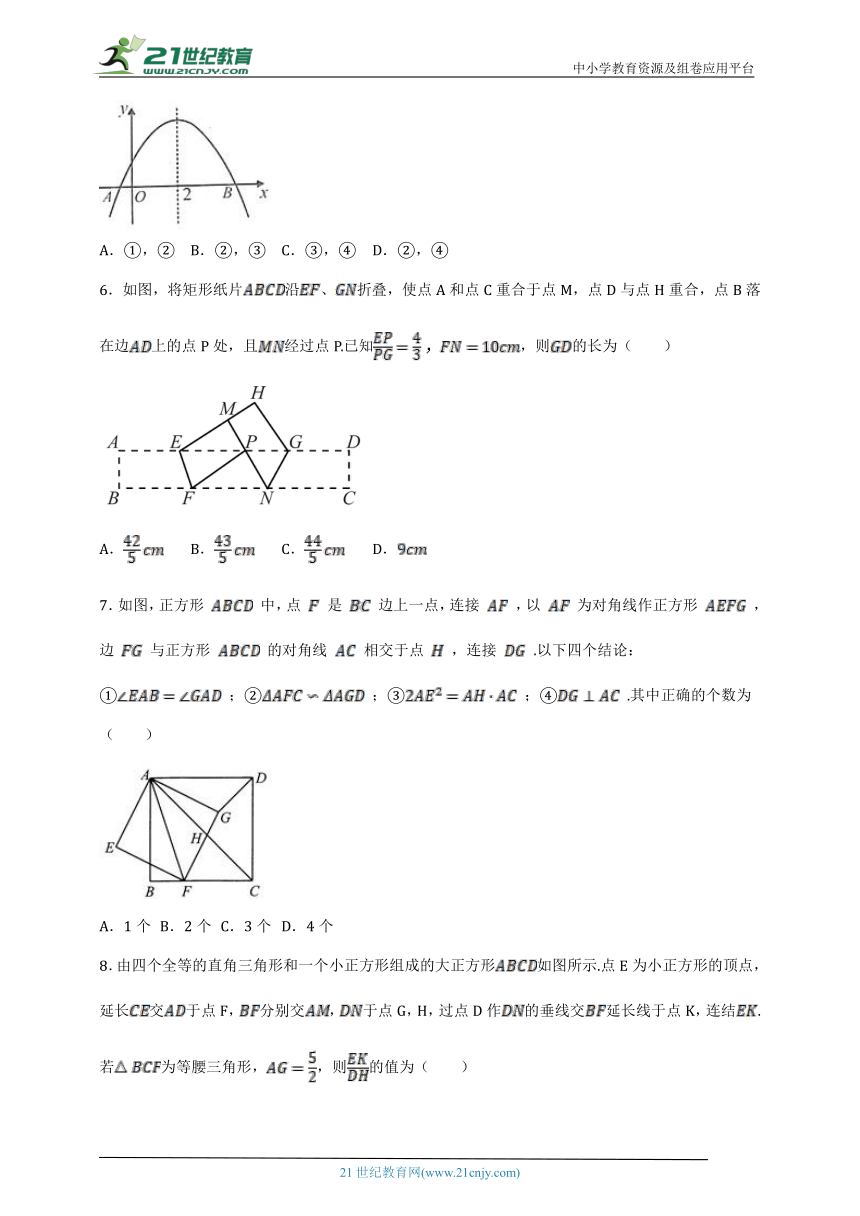
5.如图,已知二次函数 图象与x轴交于A,B两点,对称轴为直线x=2,下列结论:①abc>0; ②4a+b=0;③若点A坐标为( 1,0),则线段AB=5; ④若点M(x1,y1)、N(x2,y2)在该函数图象上,且满足0A.①,② B.②,③ C.③,④ D.②,④
6.如图,将矩形纸片沿、折叠,使点A和点C重合于点M,点D与点H重合,点B落在边上的点P处,且经过点P.已知,则的长为( )
A. B. C. D.
7.如图,正方形 中,点 是 边上一点,连接 ,以 为对角线作正方形 ,边 与正方形 的对角线 相交于点 ,连接 .以下四个结论:① ;② ;③ ;④ .其中正确的个数为( )
A.1个 B.2个 C.3个 D.4个
8.由四个全等的直角三角形和一个小正方形组成的大正方形如图所示.点E为小正方形的顶点,延长交于点F,分别交,于点G,H,过点D作的垂线交延长线于点K,连结.若为等腰三角形,,则的值为( )
A. B. C. D.
二、多选题
9.如图,、为的直径,且.然后用尺规按如下步骤作图:①作的垂直平分线,交于点E;②以点E为圆心,为半径画弧,交于点F;③以点C为圆心,为半径画弧,交于点P,M;④分别以点P、M为圆心,为半径画弧,交于点H、N.顺次连接C、M、N、H、P,可得正五边形,则下列结论正确的有( )
A. B.
C. D.为等边三角形
三、填空题
10.如图,一人乘雪橇沿坡比1: 的斜坡笔直滑下72米,那么他下降的高度为 米.
11.战国时期数学家墨子撰写的《墨经》一书中,就有“圆,一中同长也”的记载,这句话里的“中”字的意思可以理解为 .
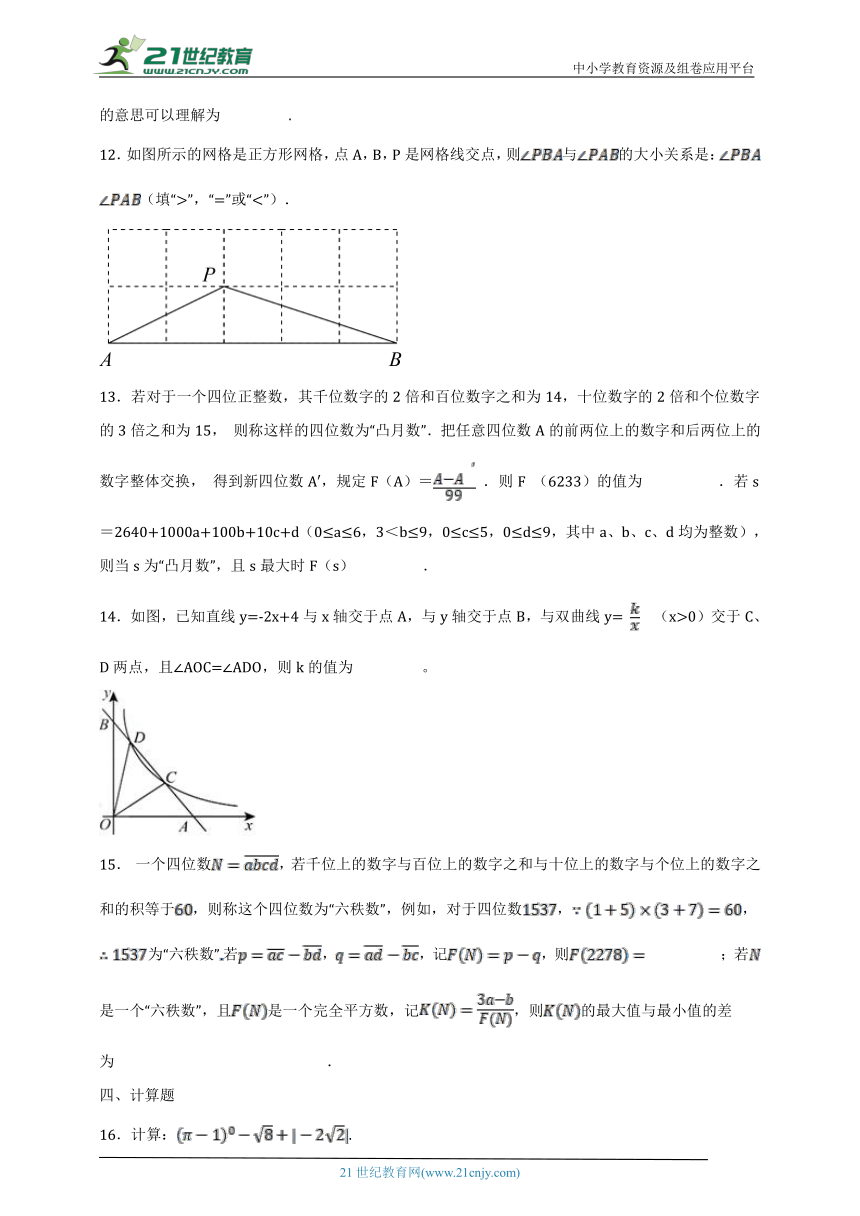
12.如图所示的网格是正方形网格,点A,B,P是网格线交点,则与的大小关系是: (填“>”,“=”或“<”).
13.若对于一个四位正整数,其千位数字的2倍和百位数字之和为14,十位数字的2倍和个位数字的3倍之和为15, 则称这样的四位数为“凸月数”.把任意四位数A的前两位上的数字和后两位上的数字整体交换, 得到新四位数A′,规定F(A)= .则F (6233)的值为 .若s=2640+1000a+100b+10c+d(0≤a≤6,3<b≤9,0≤c≤5,0≤d≤9,其中a、b、c、d均为整数),则当s为“凸月数”,且s最大时F(s) .
14.如图,已知直线y=-2x+4与x轴交于点A,与y轴交于点B,与双曲线y= (x>0)交于C、D两点,且∠AOC=∠ADO,则k的值为 。
15. 一个四位数,若千位上的数字与百位上的数字之和与十位上的数字与个位上的数字之和的积等于,则称这个四位数为“六秩数”,例如,对于四位数,,为“六秩数”若,,记,则 ;若是一个“六秩数”,且是一个完全平方数,记,则的最大值与最小值的差为 .
四、计算题
16.计算:.
17.计算: +( )﹣1﹣20170.
18.计算:.
19.解不等式组: .
五、解答题
20.为了计算花园中古树P到公路l的距离,某数学兴趣小组在公路l上的点A处,测得古树P在东北方向;从A处向正东方向行走30米,到达公路l上的点B处,再次测得古树P在北偏东的方向上,求古树P到公路l的距离.(结果保留整数,参考数据:)
21.某活动小组为了估计装有5个白球和若干个红球(每个球除颜色外都相同)的袋中红球接近多少个,在不将袋中球倒出来的情况下,分小组进行摸球球实验,试验小组两人一组,共20组,其中一名学生摸球,另一名学生记录所摸球的颜色,并将球放回袋中摇匀,每一组做400次试验,汇总起来后,摸到红球的次数为6000次.
(1)估计从袋中任意摸出1个球,恰好是红球的概率是 .
(2)请你估计袋中红球接近多少个.
22.如图1,在Rt△ABC中,∠C=90 ,AC=4cm,BC=3cm,点P由点B出发沿BA方向向点A匀速运动,速度为1cm/s;点Q由点A出发沿AC方向向点C匀速运动,速度为2cm/s;连结PQ。若设运动时间为t(s)(0(1)当t为何值时?PQ//BC?
(2)设△APQ的面积为y(cm2),求y与t之间的函数关系?
(3)是否存在某一时刻t,使线段PQ恰好把△ABC的周长和面积同时平分?若存在求出此时t的值;若不存在,说明理由.
(4)如图2,连结PC,并把△PQC沿AC翻折,得到四边形PQP'C,那么是否存在某一时刻t,使四边形PQP'C为菱形?若存在求出此时t的值;若不存在,说明理由.
23.在中,,.
(1)如图1,点在边上,且.求的值;
(2)如图2,点在的外部,且.求证:;
(3)若是平面内一点,且,,请直接写出的值为 .
六、作图题
24.
(1)如图1,已知圆 ,点 、 在圆上,且 为等边三角形,点 为直线 与圆 的一个交点.连接 , ,证明:
(2)【方法迁移】如图2,用直尺和圆规在矩形 内作出所有的点 ,使得 (不写作法,保留作图痕迹).
(3)【深入探究】已知矩形 , , , 为 边上的点,若满足 的点P恰有两个,求 的取值范围.
(4)已知矩形 , , , 为矩形 内一点,且 ,若点 绕点 逆时针旋转 到点 ,求 的最小值,并求此时 的面积.
25.在一次课题学习中活动中,老师提出了如下一个问题:
点P是正方形ABCD内的一点,过点P画直线l分别交正方形的两边于点M、N,使点P是线段MN的三等分点,这样的直线能够画几条
经过思考,甲同学给出如下画法:
如图1,过点P画PE⊥AB于E,在EB上取点M,使EM=2EA,画直线MP交AD于N,则直线MN就是符合条件的直线l.
根据以上信息,解决下列问题:
(1)甲同学的画法是否符合题意 请说明理由.
(2)在图1中,能否画出符合题目条件的直线 如果能,请直接在图1中画出.
(3)如图2,A1、C1分别是正方形ABCD的边AB、CD上的三等分点,且A1C1∥AD.当点P在线段A1C1上时,能否画出符合题目条件的直线 如果能,可以画出几条
(4)如图3,正方形ABCD边界上的A1、A2、B1、B2、C1、C2、D1、D2都是所在边的三等分点.当点P在正方形ABCD内的不同位置时,试讨论,符合题目条件的直线l的条数的情况.
七、综合题
26.如图,在 中, 平分 交 于点D, ,分别交 , 于点E,F.
(1)求证: ;
(2)若 , ,求 的度数.
27.在不透明的箱子里放有4个乒乓球,每个乒乓球上分别写有数字1、2、3、4,从箱中摸出一个球记下数字后放回箱中,摇匀后再摸出一个记下数字.若将第一次摸出的球上的数字记为点的横坐标,第二次摸出球上的数字记为点的纵坐标.
(1)请用列表法或树状图法写出两次摸球后所有可能的结果.
(2)求这样的点落在如图所示的圆内的概率(注:图中圆心在直角坐标系中的第一象限内,并且分别于x轴、y轴切于点(2,0)和(0,2)两点).
28.2022北京冬奥会期间,冰墩墩和雪容融受到人们的广泛喜爱.某网店以每套96元的价格购进了一批冰墩墩和雪容融,由于销售火爆,销售单价经过两次的调整,从每套150元上涨到每套216元,此时每天可售出16套冰墩墩和雪容融.
(1)若销售价格每次上涨的百分率相同,求每次上涨的百分率;
(2)预计冬奥会闭幕后需求会有所下降,需尽快将这批冰墩墩和雪容融售出,决定降价出售.经过市场调查发现:销售单价每降价10元,每天多卖出2套,当降价钱数m为多少元时每天的利润W(元)可达到最大,最大利润是多少?
29.在中,,是的中点,是的中点,过点作交的延长线于点,连接.
(1)求证:四边形是菱形;
(2)若,,求四边形的面积.
30.课本再现
如图1,在等边中,为边上一点,为上一点,且,连接与相交于点.
(1)与的数量关系是 ,与构成的锐角夹角的度数是 .
(2)深入探究:将图1中的延长至点,使,连接,,如图2所示.求证:平分.(第一问的结论,本问可直接使用)
(3)迁移应用:如图3,在等腰中,,,分别是边,上的点,与相交于点.若,且,求的值.
31.如图,顶点为M的抛物线 与x轴交于A、B两点(点A在点B的左边),与y轴的正半轴交于点C,已知 ,∠ACO=30°
(1)求抛物线的解析式和M的坐标;
(2)若点N是抛物线的对称轴上的一个动点,且满足△CAN是直角三角形,直接写出点N的坐标;
(3)已知点G是y轴上的一点,直接写出GC+2GB的最小值,以及此时点G的坐标.
八、实践探究题
32.
(1)【基本模型】
如图1,已知,线段AC与BD交于点P,且P为线段BD的中点.求证:;
(2)【应用模型】
如图2,在和中,,,且,,将绕点A顺时针方向旋转,把点E在AC边上时的位置作为起始位置(此时点B和点D位于AC的两侧),设旋转角为,连接BD,点P是线段BD的中点,连接PC,PE.当在起始位置时,猜想:PC与PE的数量关系和位置关系,并说明理由;
(3)【拓展迁移】
如图3,在【应用模型】的条件下,当时,点D落在AB边上,请判断PC与PE的数量关系和位置关系,并证明你的结论.
33.综合与实践
如图1,某兴趣小组计划开垦一个面积为的矩形地块种植农作物,地块一边靠墙,另外三边用木栏围住,木栏总长为.
【问题提出】
小组同学提出这样一个问题:若,能否围出矩形地块?
(1)【问题探究】
小颖尝试从“函数图象”的角度解决这个问题:
设为,为.由矩形地块面积为,得到,满足条件的可看成是反比例函数的图象在第一象限内点的坐标;木栏总长为,得到,满足条件的可看成一次函数的图象在第一象限内点的坐标,同时满足这两个条件的就可以看成两个函数图象交点的坐标.
如图2,反比例函数的图象与直线:的交点坐标为和 ,因此,木栏总长为时,能围出矩形地块,分别为:,;或 m, m.
根据小颖的分析思路,完成上面的填空.
(2)【类比探究】
若,能否围出矩形地块?请仿照小颖的方法,在图2中画出一次函数图象并说明理由.
(3)【问题延伸】
当木栏总长为时,小颖建立了一次函数.发现直线可以看成是直线通过平移得到的,在平移过程中,当过点时,直线与反比例函数的图象有唯一交点.
请在图2中画出直线过点时的图象,并求出的值.
(4)【拓展应用】
小颖从以上探究中发现“能否围成矩形地块问题”可以转化为“与图象在第一象限内交点的存在问题”.
若要围出满足条件的矩形地块,且和的长均不小于,请直接写出的取值范围.
答案解析部分
1.【答案】A
【知识点】勾股定理
【解析】【解答】解;∵直角三角形的两条直角边的长为6和8,
∴它的斜边长==10.
故答案为:A.
【分析】利用勾股定理求出斜边的长即可。
2.【答案】D
【知识点】一元二次方程根的判别式及应用
【解析】【解答】解: ∵关于x的一元二次方程有实数根,
∴△=(-2)2-4m≥0,
解得:.
故答案为:D.
【分析】由关于x的一元二次方程有实数根, 可得△≥0,据此解答即可.
3.【答案】B
【知识点】扇形面积的计算;等可能事件的概率
【解析】【解答】解:由题意得,
故答案为:B
【分析】根据扇形的面积公式结合等可能事件的概率即可求解。
4.【答案】B
【知识点】求代数式的值-整体代入求值
【解析】【解答】解: ,将 代入,原式==-3.
故答案为:B.
【分析】先将代数式的分子分母同时除以b,再将代入求值即可.
5.【答案】D
【知识点】二次函数图象与系数的关系;二次函数图象与坐标轴的交点问题;二次函数与不等式(组)的综合应用;二次函数y=ax^2+bx+c的性质
【解析】【解答】解:∵抛物线开口向下,∴a<0.∵对称轴 ,∴b=-4a>0.∵抛物线与y轴交点在y轴正半轴,∴c>0,∴abc<0,故①错误;
由①得:b=-4a,∴4a+b=0,故②正确;
若点A坐标为( 1,0),因为对称轴为x=2,∴B(5,0),∴AB=5+1=6.故③错误;
∵a<0,∴横坐标到对称轴的距离越大,函数值越小.∵0<x1<1,2<x2<3,∴ ,∴y1<y2,故④正确.
故答案为:D.
【分析】根据二次函数的性质判断即可。
6.【答案】A
【知识点】平行线的性质;矩形的判定与性质;翻折变换(折叠问题);锐角三角函数的定义
【解析】【解答】解:如图,过点作,则四边形是矩形,,
四边形是矩形,
,,,
,
,
,
折叠,
∴,
,
,
,
,
,
,
,
,
设,则,
中,,
,
,
,
,
,
,
,
,
.
故答案为:A.
【分析】过点P作PQ⊥BC,则四边形ABQP、QPDC是矩形,PD=QC,根据矩形的性质可得PQ=AB,∠EMP=∠A=90°,EP∥FN,EM∥PF,根据平行线的性质可得∠MPE=∠PNF,根据等角的余角相等可得∠1=∠2,根据折叠的性质可得∠PFE=∠BFE,∠CNG=∠GNP,根据平行线的性质可得∠PEF=∠EFB,∠PGN=∠GNC,推出PE=PF,PG=PN,根据三角函数的概念可设PF=4k,PN=3k,则FN=5k,结合FN的值可得k的值,然后求出PF、PQ、QN、NC、PD、PG,据此计算.
7.【答案】D
【知识点】正方形的性质;相似三角形的判定与性质
【解析】【解答】解:①∵四边形AEFG和四边形ABCD均为正方形
∴∠EAG=∠BAD=90°
又∵∠EAB=90°-∠BAG,∠GAD=90°-∠BAG
∴∠EAB=∠GAD
∴①正确②∵四边形AEFG和四边形ABCD均为正方形
∴AD=DC,AG=FG
∴AC= AD,AF= AG
∴ ,
即
又∵∠DAG+∠GAC=∠FAC+∠GAC
∴∠DAG=∠CAF
∴
∴②正确③∵四边形AEFG和四边形ABCD均为正方形,AF、AC为对角线
∴∠AFH=∠ACF=45°
又∵∠FAH=∠CAF
∴△HAF∽△FAC
∴
即
又∵AF= AE
∴
∴③正确④由②知
又∵四边形ABCD为正方形, AC为对角线
∴∠ADG=∠ACF=45°
∴DG在正方形另外一条对角线上
∴DG⊥AC
∴④正确
故答案为:D.
【分析】根据正方形的性质可得∠EAG=∠BAD=90°,利用同角的余角相等可得∠EAB=∠GAD,据此判断①;根据两组对边成比例且夹角相等,可证,据此判断②;先证△HAF∽△FAC,可得,可得,由AF= AE,即得,据此判断③;由,可得∠ADG=∠ACF=45°,从而求出∠AND=90°,据此判断④.
8.【答案】D
【知识点】三角形全等及其性质;勾股定理;矩形的判定与性质;正方形的性质;相似三角形的判定与性质
【解析】【解答】解:过点K作KP⊥CF,交CF的延长线于点P,DN与CF交于点O,
由题意可知:四边形NMEO和四边形ABCD是正方形,
,,,
,
是等腰三角形,
,
在和中,
,
,
,,
,
,
又,,
,
,
,
,
,
在中,,
,
,
解得:,
,,
,
又,
,
,
∵四边形,
,,
,
,
,,
,
,,
,,
,,
,,
,
,
又,
,
,
在和中,
,
,
,
由题意可得:,
,
,,
,
,
,解得,
,,
,
,
∴四边形是矩形,
,,
由题意可知:,
,
,
,
,
故答案为:D.
【分析】过点K作KP⊥CF,交CF的延长线于点P,DN与CF交于点O,易得四边形NMEO和四边形ABCD是正方形, 首先结合正方形的性质、等腰三角形的性质,可利用HL判断Rt△BAF≌Rt△CDF,得AF=DF,∠AFB=∠DFC,进而借助平行线的性质及等量代换可得∠DAM=∠AFB,由等角对等边得AG=FG,由等角的余角相等得∠BAM=∠ABF,得AG=BG=GF,在Rt△ABF中,利用勾股定理建立方程算出AF,从而可得FD、AB、AD的长,由等面积法求出BE,由勾股定理算出EF,进而判断出△BMG∽△BEF,由相似三角形对应边成比例建立方程可求出MG、BM,利用ASA判断出△KFD≌△GFA得KF=KD=AG=GF,由题意得Rt△BEC≌Rt△DNA,得DN=BE=4,进而再判断出△HNG∽△HDK,由相似三角形对应边成比例建立方程可求出NH,证出四边形PODK是矩形,得PK=DO=2,PO=KD=,由题意得Rt△BEC≌Rt△COD,得OC=BE=4,由勾股定理算出KE,从而即可求出答案.
9.【答案】A,B
【知识点】圆的综合题
【解析】【解答】设则,
∴,,
∵,
∴,
故B符合题意;
∵,,
∴直线不是线段的垂直平分线,
∴,
∴不是等边三角形,
故D不符合题意;
如图,连接,
∵正五边形,,
∴,,,
∴,,,
∴,,,
∴,,
∴,
∴,
故A符合题意;
∵无法计算,
故D不符合题意;
故答案为:A、B.
【分析】利用全等三角形的判定方法和性质,圆的弧、弦及圆周角的关系逐项判断即可。
10.【答案】36
【知识点】解直角三角形的实际应用﹣坡度坡角问题
【解析】【解答】如图:
因为坡度比为1: ,即tanα= ,
∴α=30°.
则其下降的高度=72×sin30°=36米.
故答案为36
【分析】先求出tanα= ,再求出α=30°,最后利用锐角三角函数值计算求解即可。
11.【答案】圆心
【知识点】圆的认识
【解析】【解答】解: 战国时期的《墨经》一书中记载:“圜(圆),一中同长也”,表示圆心到圆上各点的距离都相等,即半径都相等.
故答案为:圆心 .
【分析】 根据圆的几要素,作出判断.
12.【答案】<
【知识点】三角形三边关系;勾股定理
【解析】【解答】解:,,
,
.
故答案为:<.
【分析】利用勾股定理求出AP、BP的长,再比较AP、BP的长,根据三角形中大边对大角即可求解.
13.【答案】29;9
【知识点】定义新运算
【解析】【解答】解:(1)∵6×2+2=14,3×2+3×3=15
∴6233是“凸月数”
∴
故答案为:29
(2)当0≤b<4时
∵s=2640+1000a+100b+10c+d为“凸月数”
∴2(a+2)+(b+6)=14,2(c+4)+3d=15
即2a+b=4,2c+3d=7
∵0≤a≤6,3<b≤9,0≤c≤5,0≤d≤9,其中a、b、c、d均为整数
∴a=1,b=2(或a=2,b=0),c=2,d=1
∴s=3861或4661
当4≤b≤7时
∵s=2640+1000a+100b+10c+d为“凸月数”
∴2(a+3)+(b-4)=14,2(c+4)+3d=15
即2a+b=12,2c+3d=7
∵0≤a≤6,3<b≤9,0≤c≤5,0≤d≤9,其中a、b、c、d均为整数
∴a=3,b=6(或a=4,b=4,),c=2,d=1
∴s=6261或7061
故满足条件s的值为3861或4661或6261或7061
当s=7061时,
故答案为:9
【分析】(1)根据新定义先判断6233为“凸月数”,即可求出答案.
(2)分当0≤b<4时,当4≤b≤7时,根据新定义列出方程,解方程即可求出答案.
14.【答案】
【知识点】勾股定理;平行四边形的判定与性质;相似三角形的判定与性质
【解析】【解答】解:
根据已知可得,OA=2,OB=4,根据勾股定理可得,AB=2
如图,过点C作CE⊥x轴于点E,作CG⊥y轴于点G,过点D作DH⊥x轴于点H,作DF⊥y轴于点F,连接GH,GD,CH
∵点C和点D为反比例函数图象上的点
∴S矩形FDHO=S矩形GCEO
∴S矩形FDHO=S矩形GOEC
∴S△DGH=S△GHC
∴点C,D到GH的距离相等
∴CD∥GH
∴四边形BDHG和四边形GHAC都是平行四边形
∴BD=GH,GH=CA
即BD=AC
设AC=BD=m
∵∠AOC=∠ADO,∠CAO=∠DAO
∴△AOC∽△ADO
∴
∴AO2=AC×AD
∴22=m(2-m)
∴m=+1(舍去),m=-1
过点C作CE⊥x轴于点E
∴△ACE∽△ABO
∴
∴
∴AE=,CE=
∴OE=OA-AE=2-=
∴CE×OE=×=
【分析】如图,过点C作CE⊥x轴于点E,作CG⊥y轴于点G,过点D作DH⊥x轴于点H,作DF⊥y轴于点F,连接GH,GD,CH,根据勾股定理计算得到AB的长度,根据平行四边形的判定和性质以及相似三角形的判定和对应边成比例,计算得到答案即可。
15.【答案】;,,,,
【知识点】定义新运算
【解析】【解答】解:设,
即,
整理得,
故F.
根据题意是一个“六秩数”,且是一个完全平方数,
则满足,且是一个完全平方数,
是一个完全平方数,
故或,
当时,根据进行推算:
,,此时,故,
若,,则,
若,,则,
若,,则,
若,,则,
的最大值与最小值的差为:;
,,此时,故,
若,,则,
若,,舍去,
若,,则,
若,,舍去,
若,,舍去,
若,,舍去,
若,,则,
若,,舍去,
若,,则,
的最大值与最小值的差为:;
,,此时,故,舍去,
,,此时,故
若,,则,
若,,舍去
若,,舍去
若,,舍去
若,,则,
的最大值与最小值的差为:;
,,此时,故,
若,,则,
若,,则,
若,,则,
若,,则,
的最大值与最小值的差为:;
,,此时,故,舍去,
,,此时,故,舍去,
,,此时,故,舍去,
当时,根据进行推算:
,,此时,故,
若,,舍去,
若,,则,
若,,舍去,
若,,则,
若,,舍去,
的最大值与最小值的差为:;
综上,的最大值与最小值的差为:,,,,;
故答案为:;,,,,.
【分析】根据“六秩数”的定义,结合题意计算求解即可。
16.【答案】解:原式
;
【知识点】二次根式的混合运算;实数的混合运算(含开方)
【解析】【分析】先根据0指数幂的性质、二次根式的性质及绝对值的性质分别化简,再合并同类二次根式即可。
17.【答案】解:原式=2+2﹣1=3
【知识点】实数的运算;零指数幂;负整数指数幂
【解析】【分析】首先计算开方,乘方、然后计算乘法,最后从左向右依次计算,求出算式的值是多少即可.
18.【答案】解:原式=6+3×2
=2+18
=24
【知识点】二次根式的混合运算
【解析】【分析】先利用二次根式的乘法法则计算,再计算加法即可.
19.【答案】解:解不等式 ,得: ,
解不等式 ,得: ,
则不等式组的解集为 .
【知识点】解一元一次不等式组
【解析】【分析】分别求出每一个不等式的解集,根据口诀:同大取大、同小取小、大小小大中间找、大大小小找不到确定不等式组的解集.
20.【答案】解:过点P作于点C,设,
由题意可知,
则.
∴在中,
,
∵在中,,
∴,
则,
∴,
∴,
则古树P到公路l的距离约为.
【知识点】解直角三角形的实际应用﹣方向角问题
【解析】【分析】过点P作PC⊥l于点C,设BC=x,根据题意可得到∠PAC=45°,∠PBC=60°,利用解直角三角形表示出PC的长,同时可证得AC=PC,据此可得到关于x的方程,解方程求出x的值,可得到PC的长.
21.【答案】(1)
(2)解:有(1)可知,摸到白球的概率约为1-=,
所以总球数=5=20(个),
所以袋中红球数约为20-5=15(个).
【知识点】利用频率估计概率;概率公式
【解析】【解答】(1)从袋中任意摸出1个球,恰好是红球的概率==;
故答案为:;
【分析】(1)根据用频率估算概率,可以得到摸到红球的概率为;
(2)根据用样本估算总体的定义,可得袋中总的球数;最后根据红球数=总球数-白球的数量,可得红球的数量.
22.【答案】解:(1) 连接PQ,
若=时,PQ//BC,即=,
∴ t=
(2) 过P作PD⊥AC于点D,则有=,
即=,
∴ PD=(5-t)
∴ y=·2t·(5-t)=-+4t(0(3) 若平分周长则有:
AP+AQ=(AB+AC+BC),
即:5-t+2t=6,
∴ t=1
当t=1时,y=3.4;而三角形ABC的面积为6,显然不存在.
过P作PD⊥AC于点D,若QD=CD,则PQ=PC,四边形PQP'C就为菱形.
同(2)方法可求AD=(5-t),所以:
(5-t)-2t=4-(5-t);
解之得:t=.
即t=时,四边形PQP'C为菱形.
【知识点】二次函数的最值;菱形的判定;平行线分线段成比例
【解析】【分析】(1)当PQ∥BC时,我们可得出三角形APQ和三角形ABC相似,那么可得出关于AP,AB,AQ,AC的比例关系,我们观察这四条线段,已知的有AC,根据P,Q的速度,可以用时间t表示出AQ,BP的长,而AB可以用勾股定理求出,这样也就可以表示出AP,那么将这些数值代入比例关系式中,即可得出t的值.
(2)求三角形APQ的面积就要先确定底边和高的值,底边AQ可以根据Q的速度和时间t表示出来.关键是高,可以用AP和∠A的正弦值来求.AP的长可以用AB-BP求得,而sinA就是BC:AB的值,因此表示出AQ和AQ边上的高后,就可以得出y与t的函数关系式.
(3)如果将三角形ABC的周长和面积平分,那么AP+AQ=BP+BC+CQ,那么可以用t表示出CQ,AQ,AP,BP的长,那么可以求出此时t的值,我们可将t的值代入(2)的面积与t的关系式中,求出此时面积是多少,然后看看面积是否是三角形ABC面积的一半,从而判断出是否存在这一时刻.
(4)过点P作PM⊥AC于M,PN⊥BC于N,那么PNCM就是个矩形,解题思路:通过三角形BPN和三角形ABC相似,得出关于BP,PN,AB,AC的比例关系,即可用t表示出PN的长,也就表示出了MC的长,要想使四边形PQP'C是菱形,PQ=PC,根据等腰三角形三线合一的特点,QM=MC,这样有用t表示出的AQ,QM,MC三条线段和AC的长,就可以根据AC=AQ+QM+MC来求出t的值.求出了t就可以得出QM,CM和PM的长,也就能求出菱形的边长了.
23.【答案】(1)解:,
,
(2)证明:如图,将AE绕点A逆时针旋转120°,得到AF,连接CF,EF,过点A作AH⊥EF于H,
∴AE=AF,∠EAF=120°,
∴∠AEF=∠AFE=30°,
∵AH⊥EF,
∴AH=12AE,FH=EH,EH=√3AH,
∴EF=√3AE,
∵∠BAC=∠EAF=120°,
∴∠BAE=∠CAF,
又∵AB=AC,AE=AF,
∴△BAE≌△CAF(SAS),
∴∠BEA=∠AFC,BE=CF,
设∠BEA=∠AFC=x,
∴∠FEC=∠BEC x 30°,
∵2∠BEC ∠AEB=270°,
∴∠BEC=135°+,
∴∠FEC=105° ,
∵∠EFC=∠AFC ∠AFE=x 30°,
∴∠FEC=180° (x 30°) (105 x2)=105° ,
∴∠FEC=∠FCE,
∴EF=CF=BE=AE;
(3)
【知识点】三角形内角和定理;含30°角的直角三角形;旋转的性质;等腰直角三角形;三角形全等的判定(SAS)
【解析】【解答】解:(3)如图,当点P在△ABC内时,将△APC绕点A顺时针旋转120°,得到△AHB,连接HP,
∵∠APB=90°,∠BPC=150°,
∴∠APC=120°,∠PBC+∠PCB=30°,
∴∠ABP+∠ACP=30°,
∵将△APC绕点A顺时针旋转120°,得到△AHB,
∴AP=AH,∠HAP=120°,BH=PC,∠ACP=∠ABH,∠APC=∠AHB=120°,
∴∠AHP=∠APH=30°,∠ABP+∠ABH=30°,
∴∠PHB=90°,∠PBH=30°,
∴BP=2HP,BH=HP,
∴BP=BH=PC,
∴;
如图,当点P在△ABC外时,将△APC绕点A顺时针旋转120°,得到△AHB,连接HP,
∵∠APB=90°,∠BPC=150°,
∴∠APC=60°,∠PBC+∠PCB=30°,
∴∠ABP+∠ACP=90°,
∵将△APC绕点A顺时针旋转120°,得到△AHB,
∴AP=AH,∠HAP=120°,BH=PC,∠ACP=∠ABH,∠APC=∠AHB=60°,
∴∠AHP=∠APH=30°,∠ABP+∠ABH=90°,
∴∠PHB=30°,∠PBH=90°,
∴BH=BP,
∴PC=BP,
∴PCBP=,
综上所述:=或,
故答案为:或.
【分析】(1)由等腰三角形的性质可得∠B=∠C=30°,由角的数量关系可求∠ABC=30°,∠BAD=90°,由直角三角形的性质可得BD=2AD=2CD,即可求解;
(2)将AE绕点A逆时针旋转120°,得到AF,过点A作AH⊥EF于H,由等腰三角形的性质可求EF与AE的数量关系,由“SAS”可证ΔBAE≌ΔCAF,可得∠BEA=∠AFC,BE=CF,由角的数量关系可证∠FEC=∠FCE,可证EF=CF=BE=AE;
(3)分两种情况讨论,由旋转的性质可得AP=AH,∠HAP=120°,BH=PC、∠ACP=∠ABH、∠APC=∠AHB=120°,由直角三角形的性质可求解.
24.【答案】(1)解:如图1所示,连接AP,BP.
∵ 为等边三角形,
∴∠AOB=60°.
∵∠APB= ∠AOB,
∴∠APB=30°.
(2)解:如图2所示:点P在 上即可.
(3)解:由(2)得,要使 的点P恰有两个,则AD与 相交,如图3所示,
①当AD与⊙O相切时,连接OP,并延长PO与BC相交于Q,
∵AD与⊙O相切,
∴∠APQ=90°,
∵四边形ABCD是矩形,
∴∠A=∠ABQ=90°.
∴∠A=∠ABQ=∠APQ=90°.
∴四边形ABQP为矩形,
∴PQ=AB=m.
∵△BOC是等腰直角三角形,
∴OQ= BC= ,OB=2.
∴PQ=2+ .
∴m<2+ .
②当AD与EF重合时,
m=BE=BC=2
综上所述,m的取值范围为:2 ≤m<2+ .
(4)解:如图4所示:
依题意可知,当A,P,O在同一直线上时,AP有最小值,此时PQ最小.
过点O作OH⊥BC于H,作OG⊥AB于G,过点P作PM⊥AB于M,连接OP,OB.
∵∠GBH=90°,
∴四边形BGOH为矩形,
∴OG=BH= BC= .
∵∠BPC=120°,
∴∠BOC=120°,
∵OB=OC,
∴∠OBH=30°.
∴设OH=x,则OB=2x.
在Rt△OBH中
OB2-OH2=BH2,
即4x2-x2=( )2,
解得:x=1.
∴OH=1,OB=2.
∵AB=3,
∴AG=4.
在Rt△AGO中
OA= =
∴AP= -2.
根据旋转的性质可知,AQ=AP= -2,∠PAQ=90°,
根据勾股定理可求得:PQ= = AP= -2 .
∵OG⊥AB,PM⊥AB
∴PM∥OG,
∴ =
∵OG= ,AP= -2,OA=
∴PM= .
∴ 的面积= AB PM= 3 = .
答: 的最小值为 -2 .,并求此时 的面积是 .
【知识点】圆的综合题
【解析】【分析】(1)如图1所示,连接AP,BP.利用等边三角形的性质可得∠AOB=60°,根据圆周角定理可得∠APB= ∠AOB,据此求出结论;
(2)作出正方形BCFE,然后作出其外接圆,点P在 上即可;
(3)由(2)得,要使 的点P恰有两个,则AD与 相交,如图3所示,①当AD与⊙O相切时,连接OP,并延长PO与BC相交于Q,据此求出最大值;②当AD与EF重合时,据此求出最小值;从而求出m的范围;
(4)如图4所示,当A,P,O在同一直线上时,AP有最小值,此时PQ最小.过点O作OH⊥BC于H,作OG⊥AB于G,过点P作PM⊥AB于M,连接OP,OB. 先求出∠OBH=30°,设OH=x,则OB=2x.
在Rt△OBH中,利用勾股定理求出OH=1,OB=2.在Rt△AGO中,利用勾股定理求出OA=,从而可得AP=-2,利用旋转的性质可得AQ=AP= -2,∠PAQ=90°,根据勾股定理可得PQ=AP= -2 . 根据平行线分线段成比例可得 = ,据此求出PM的长,由 的面积= AB PM计算即可.
25.【答案】(1)解:甲同学的画法符合题意.
∵PE∥AD,
∴△MPE~△MNA,
∴ ,
∵EM=2EA,
∴MP:MN=2:3,
∴点P是线段MN的一个三等分点;
(2)解:能画出一个符合题目条件的直线,在EB上取M1,使EM1= AE,直线M1P就是满足条件的直线,如图1;
(3)解:若点P在线段A1C1上,能够画出符合题目条件的直线无数条,如图2;
(4)解:若点P在A1C1,A2C2,B1D1,B2D2上时,可以画出无数条符合条件的直线l;
当点P在正方形A0B0C0D0内部时,不存在这样的直线l,使得点P是线段MN的三等分点;
当点P在矩形ABB1D1,CDD2B2,A0D0D2D1,B0B1B2C0内部时,过点P可画出两条符合条件的直线l,使得点P是线段MN的三等分点.
【知识点】正方形的性质;相似三角形的判定与性质
【解析】【分析】(1)利用△MPE∽△MNA中的成比例线段可知EM=2EA,所以MP:MN=2:3,即点P是线段MN的一个三等分点;(2)由(1)中的证明过程可知,在EB上取M1,使EM1= AE,直线M1P就是满足条件的直线,所以能画出一条符合题目条件的直线;(3)当点P在线段A1C1上,根据正方形的性质可知能够画出符合题目条件的直线有无数条;(4)分情况讨论.
26.【答案】(1)证明:∵ 平分 , ,
∴ ,
∵AF=AF,
∴△AFE≌△AFC(ASA),
∴ ;
(2)解:由(1)可得△AFE≌△AFC,
∴∠AEC=∠ACE,
∵ , ,
∴∠AEC=∠ACE=40°,
∴ .
【知识点】垂线;三角形的外角性质;三角形全等的判定(ASA);角平分线的定义
【解析】【分析】(1)由角平分线易得 ,根据 可得 ,易证 △AFE≌△AFC 可得结果;
(2)由 , 可得 ∠ACE=40°, 由(1)可得 ∠AEC=∠ACE ,根据三角形外角性质可得结果.
27.【答案】(1)解:列表得:
第一次 第二次 1 2 3 4
1 (1,1) (2,1) (3,1) (4,1)
2 (1,2) (2,2) (3,2) (4,2)
3 (1,3) (2,3) (3,3) (4,3)
4 (1,4) (2,4) (3,4) (4,4)
则共有16种等可能的结果;
(2)解:∵这样的点落在如图所示的圆内的有:(1,1),(1,2),(1,3),(2,1),(2,2),(2,3),(3,1),(3,2),(3,3),
∴这样的点落在如图所示的圆内的概率为:
【知识点】列表法与树状图法
【解析】【分析】(1)首先根据题意列出表格,然后由表格即可求得所有等可能的结果;(2)根据(1)中的表格求得这样的点落在如图所示的圆内的情况,然后利用概率公式求解即可求得答案.
28.【答案】(1)解:设每次上涨的百分率为x,根据题意得:
,
解得:(不合题意,舍去),
答:每次上涨的百分率为;
(2)解:根据题意得:
∴当m=20时,W最大,最大值为2000,
答:当降价钱数m为20元时,每天的利润W可达到最大,最大利润是2000元.
【知识点】一元二次方程的实际应用-百分率问题;二次函数的实际应用-销售问题
【解析】【分析】(1)设每次上涨的百分率为x,根据题意列出方程,再求解即可;
(2)根据题意列出函数解析式,再利用二次函数的性质求解即可。
29.【答案】(1)证明:∵是的中点,
∴,
∵,
∴,
又∵,
∴,
∴,
∵,是的中点,
∴,
∴四边形为平行四边形,
又∵,
∴平行四边形为菱形;
(2)解:,
由题意可得:,
【知识点】菱形的判定;几何图形的面积计算-割补法
【解析】【分析】(1)先证明四边形为平行四边形,再结合AD=CD,可得平行四边形为菱形;
(2)利用割补法求出即可。
30.【答案】(1);
(2)证明:∵,,
∴是等边三角形,
∴,.
∵在等边中,,,
∴,
∴,
∴,
∴,
∴,
∴平分.
(3)解:如图,延长至,使得,连接,,过点作,交于点.
设.
∵,,
∴,
∴,
∴,
∴.
∵,即,
∴,
∴,,
∴,.
∵,
∴,
∴,,
∴.
【知识点】三角形的外角性质;等边三角形的判定与性质;相似三角形的判定与性质;三角形全等的判定(SAS)
【解析】【解答】(1)解:∵是等边三角形,
∴,
∵,
∴,
∴,
∴;
故答案为:;
【分析】(1)根据SAS证明△ABE≌△CAD,可得AD=BE,∠ABE=∠CAD,根据三角形的外角的性质可得;
(2)根据SAS证明△ABF≌△CBG,可得, 根据角的和差求出∠CGA=60°,根据角平分线的定义即得结论;
(3) 延长至,使得,连接,,过点作,交于点. 根据两边成比例且夹角相等可证,可得,再证, 可得 , ∠CHA=∠BHG,利用平行线的性质可得, 从而得出,, 从而得出.
31.【答案】(1)解:根据题意,当 时,
∴ ,即
∵
∴
∵
∴
∴
又∵
∴
∴
∴
∴抛物线对称轴为:
当 时,
∴ ;
(2) 或 或 ;
(3)GC+2GB的最小值 ,
【知识点】线段的性质:两点之间线段最短;含30°角的直角三角形;勾股定理的逆定理;锐角三角函数的定义
【解析】【解答】解:(2)解:点N是抛物线的对称轴上的一个动点,设点N的坐标为:
根据题意得:
根据题意,△CAN是直角三角形,分 、 、 三种情况分析;
第一种情况, ,如下图:
∴
∴
∴
∴
第二种情况, ,如下图:
∴
∴
∴
∴
∴ ;
第三种情况, ,如下图:
∴
∴
∴
∴
∴ ;
∴ 或 或 ;
(3)∵
当 , 或
∵点A在点B的左边
∴
∴
∴
如图,连接GB,过点G做 交AC于点Q
∵∠ACO=30°
∴ ,∠CAO=60°
如下图,连接BQ,BQ交y轴于点P
当点G和点P重合时, 最短,即
∴ 最小值为:
如图,点G和点P重合,此时 交AC于点Q
∵∠CAO=60°,
∴
∴
∴ ,即 最小值为
∵∠CAO=60°
∴
∴
∴
∴ .
【分析】 (1)根据点A的坐标,再直角三角形含30°角的性质利用三角函数求出OC长,确定C的坐标可得n=2,再将点A的坐标代入抛物线的解析式,再配方即可求得顶点M的坐标;
(2)设N(1,n),根据两点的距离公式求得AC为16,CN2=12+(n-2)2,
AN2=(1+2)2+n2=9+n2,当△CAN是直角三角形时,分三种情况,根据勾股定理列方程求解即可;
(3)根据( 1)的结论,首先计算得OB、AB;连接GB,过点G做GQ⊥AC交AC于点Q,根据三角函数性质得QG=GC;再根据两点之间线段最短的性质,得GC+GB最小值为:QB;再根据三角函数的性质计算即可得到结果.
32.【答案】(1)证明:
∵,
∴,
∵点P为BD中点,
∴
在和中,
∴(ASA)
(2)解:,,理由如下:
如图2,延长EP交BC于F,
∵,
∴,
∴,
∵点P是线段BD的中点,
∴,
又∵,
∴(ASA),
∴,,
又∵,,
∴,
又∵,
∴是等腰直角三角形,
∵,
∴,;
(3)解:,,理由如下:
如图3,过点B作,交EP延长线于点F,连接CE,CF,
同理(2)可证,
∴,,
∵,
∴,
∵当时,,
∴,,
∵,
∴,
∴,
∴,
在和中,
∴(SAS)
∴,,
∴
∴
∴是等腰直角三角形,
∵,
∴,
【知识点】旋转的性质;三角形全等的判定(ASA);三角形的综合
【解析】【分析】(1)利用“ASA”证明即可;
(2)先证明是等腰直角三角形,再结合EP=FP可得,;
(3)先利用“SAS”证明可得 ,, 再证明 是等腰直角三角形, 结合EP=FP可得 , 。
33.【答案】(1);4;2
(2)解:不能围出.
∵木栏总长为,
∴,则,
画出直线的图象,如图中所示:
∵与函数图象没有交点,
∴不能围出面积为的矩形;
(3)解:如图中直线所示,即为图象,
将点代入,得:,
解得;
(4)解:根据题意可得∶ 若要围出满足条件的矩形地块, 与图象在第一象限内交点的存在问题,
即方程有实数根,
整理得:,
∴,
解得:,
把代入得:,
∴反比例函数图象经过点,
把代入得:,解得:,
∴反比例函数图象经过点,
令,,过点,分别作直线的平行线,
由图可知,当与图象在点A左边,点B右边存在交点时,满足题意;
把代入得:,
解得:,
∴.
【知识点】一元二次方程根的判别式及应用;一次函数的图象;待定系数法求反比例函数解析式
【解析】【解答】解:(1)∵反比例函数,直线:,
∴联立可得方程组:,
解得:,,
∴反比例函数的图象与直线:的交点坐标为和 (4,2);
∴木栏总长为时,能围出矩形地块,分别为:,;或 4m,BC=2m,
故答案为:(4,2);4;2.
【分析】(1)根据题意先求出方程组:,再求出,,最后求解即可;
(2)根据题意先求出 , 再根据 与函数图象没有交点, 计算求解即可;
(3)将点代入,求出, 最后作图求解即可;
(4)利用一元二次方程根的判别式求出 , 再利用待定系数法求出 反比例函数图象经过点, 最后列方程计算求解即可。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
初中数学(通用版)九年级历年中考常考知识点综合练习题02(精华)
一、单选题
1.直角三角形的两条直角边的长分别为6和8,则斜边长为( )
A.10 B.5 C.4 D.3
2.关于x的一元二次方程有实数根,则m的取值范围是( )
A. B. C. D.
3.为增强班级凝聚力,吴老师组织开展了一次主题班会.班会上,他设计了一个如图的飞镖靶盘,靶盘由两个同心圆构成,小圆半径为,大圆半径为,每个扇形的圆心角为60度.如果用飞镖击中靶盘每一处是等可能的,那么小全同学任意投掷飞镖1次(击中边界或没有击中靶盘,则重投1次),投中“免一次作业”的概率是( )
A. B. C. D.
4.已知,则的值是( )
A.3 B.-3 C. D.-
5.如图,已知二次函数 图象与x轴交于A,B两点,对称轴为直线x=2,下列结论:①abc>0; ②4a+b=0;③若点A坐标为( 1,0),则线段AB=5; ④若点M(x1,y1)、N(x2,y2)在该函数图象上,且满足0
6.如图,将矩形纸片沿、折叠,使点A和点C重合于点M,点D与点H重合,点B落在边上的点P处,且经过点P.已知,则的长为( )
A. B. C. D.
7.如图,正方形 中,点 是 边上一点,连接 ,以 为对角线作正方形 ,边 与正方形 的对角线 相交于点 ,连接 .以下四个结论:① ;② ;③ ;④ .其中正确的个数为( )
A.1个 B.2个 C.3个 D.4个
8.由四个全等的直角三角形和一个小正方形组成的大正方形如图所示.点E为小正方形的顶点,延长交于点F,分别交,于点G,H,过点D作的垂线交延长线于点K,连结.若为等腰三角形,,则的值为( )
A. B. C. D.
二、多选题
9.如图,、为的直径,且.然后用尺规按如下步骤作图:①作的垂直平分线,交于点E;②以点E为圆心,为半径画弧,交于点F;③以点C为圆心,为半径画弧,交于点P,M;④分别以点P、M为圆心,为半径画弧,交于点H、N.顺次连接C、M、N、H、P,可得正五边形,则下列结论正确的有( )
A. B.
C. D.为等边三角形
三、填空题
10.如图,一人乘雪橇沿坡比1: 的斜坡笔直滑下72米,那么他下降的高度为 米.
11.战国时期数学家墨子撰写的《墨经》一书中,就有“圆,一中同长也”的记载,这句话里的“中”字的意思可以理解为 .
12.如图所示的网格是正方形网格,点A,B,P是网格线交点,则与的大小关系是: (填“>”,“=”或“<”).
13.若对于一个四位正整数,其千位数字的2倍和百位数字之和为14,十位数字的2倍和个位数字的3倍之和为15, 则称这样的四位数为“凸月数”.把任意四位数A的前两位上的数字和后两位上的数字整体交换, 得到新四位数A′,规定F(A)= .则F (6233)的值为 .若s=2640+1000a+100b+10c+d(0≤a≤6,3<b≤9,0≤c≤5,0≤d≤9,其中a、b、c、d均为整数),则当s为“凸月数”,且s最大时F(s) .
14.如图,已知直线y=-2x+4与x轴交于点A,与y轴交于点B,与双曲线y= (x>0)交于C、D两点,且∠AOC=∠ADO,则k的值为 。
15. 一个四位数,若千位上的数字与百位上的数字之和与十位上的数字与个位上的数字之和的积等于,则称这个四位数为“六秩数”,例如,对于四位数,,为“六秩数”若,,记,则 ;若是一个“六秩数”,且是一个完全平方数,记,则的最大值与最小值的差为 .
四、计算题
16.计算:.
17.计算: +( )﹣1﹣20170.
18.计算:.
19.解不等式组: .
五、解答题
20.为了计算花园中古树P到公路l的距离,某数学兴趣小组在公路l上的点A处,测得古树P在东北方向;从A处向正东方向行走30米,到达公路l上的点B处,再次测得古树P在北偏东的方向上,求古树P到公路l的距离.(结果保留整数,参考数据:)
21.某活动小组为了估计装有5个白球和若干个红球(每个球除颜色外都相同)的袋中红球接近多少个,在不将袋中球倒出来的情况下,分小组进行摸球球实验,试验小组两人一组,共20组,其中一名学生摸球,另一名学生记录所摸球的颜色,并将球放回袋中摇匀,每一组做400次试验,汇总起来后,摸到红球的次数为6000次.
(1)估计从袋中任意摸出1个球,恰好是红球的概率是 .
(2)请你估计袋中红球接近多少个.
22.如图1,在Rt△ABC中,∠C=90 ,AC=4cm,BC=3cm,点P由点B出发沿BA方向向点A匀速运动,速度为1cm/s;点Q由点A出发沿AC方向向点C匀速运动,速度为2cm/s;连结PQ。若设运动时间为t(s)(0
(2)设△APQ的面积为y(cm2),求y与t之间的函数关系?
(3)是否存在某一时刻t,使线段PQ恰好把△ABC的周长和面积同时平分?若存在求出此时t的值;若不存在,说明理由.
(4)如图2,连结PC,并把△PQC沿AC翻折,得到四边形PQP'C,那么是否存在某一时刻t,使四边形PQP'C为菱形?若存在求出此时t的值;若不存在,说明理由.
23.在中,,.
(1)如图1,点在边上,且.求的值;
(2)如图2,点在的外部,且.求证:;
(3)若是平面内一点,且,,请直接写出的值为 .
六、作图题
24.
(1)如图1,已知圆 ,点 、 在圆上,且 为等边三角形,点 为直线 与圆 的一个交点.连接 , ,证明:
(2)【方法迁移】如图2,用直尺和圆规在矩形 内作出所有的点 ,使得 (不写作法,保留作图痕迹).
(3)【深入探究】已知矩形 , , , 为 边上的点,若满足 的点P恰有两个,求 的取值范围.
(4)已知矩形 , , , 为矩形 内一点,且 ,若点 绕点 逆时针旋转 到点 ,求 的最小值,并求此时 的面积.
25.在一次课题学习中活动中,老师提出了如下一个问题:
点P是正方形ABCD内的一点,过点P画直线l分别交正方形的两边于点M、N,使点P是线段MN的三等分点,这样的直线能够画几条
经过思考,甲同学给出如下画法:
如图1,过点P画PE⊥AB于E,在EB上取点M,使EM=2EA,画直线MP交AD于N,则直线MN就是符合条件的直线l.
根据以上信息,解决下列问题:
(1)甲同学的画法是否符合题意 请说明理由.
(2)在图1中,能否画出符合题目条件的直线 如果能,请直接在图1中画出.
(3)如图2,A1、C1分别是正方形ABCD的边AB、CD上的三等分点,且A1C1∥AD.当点P在线段A1C1上时,能否画出符合题目条件的直线 如果能,可以画出几条
(4)如图3,正方形ABCD边界上的A1、A2、B1、B2、C1、C2、D1、D2都是所在边的三等分点.当点P在正方形ABCD内的不同位置时,试讨论,符合题目条件的直线l的条数的情况.
七、综合题
26.如图,在 中, 平分 交 于点D, ,分别交 , 于点E,F.
(1)求证: ;
(2)若 , ,求 的度数.
27.在不透明的箱子里放有4个乒乓球,每个乒乓球上分别写有数字1、2、3、4,从箱中摸出一个球记下数字后放回箱中,摇匀后再摸出一个记下数字.若将第一次摸出的球上的数字记为点的横坐标,第二次摸出球上的数字记为点的纵坐标.
(1)请用列表法或树状图法写出两次摸球后所有可能的结果.
(2)求这样的点落在如图所示的圆内的概率(注:图中圆心在直角坐标系中的第一象限内,并且分别于x轴、y轴切于点(2,0)和(0,2)两点).
28.2022北京冬奥会期间,冰墩墩和雪容融受到人们的广泛喜爱.某网店以每套96元的价格购进了一批冰墩墩和雪容融,由于销售火爆,销售单价经过两次的调整,从每套150元上涨到每套216元,此时每天可售出16套冰墩墩和雪容融.
(1)若销售价格每次上涨的百分率相同,求每次上涨的百分率;
(2)预计冬奥会闭幕后需求会有所下降,需尽快将这批冰墩墩和雪容融售出,决定降价出售.经过市场调查发现:销售单价每降价10元,每天多卖出2套,当降价钱数m为多少元时每天的利润W(元)可达到最大,最大利润是多少?
29.在中,,是的中点,是的中点,过点作交的延长线于点,连接.
(1)求证:四边形是菱形;
(2)若,,求四边形的面积.
30.课本再现
如图1,在等边中,为边上一点,为上一点,且,连接与相交于点.
(1)与的数量关系是 ,与构成的锐角夹角的度数是 .
(2)深入探究:将图1中的延长至点,使,连接,,如图2所示.求证:平分.(第一问的结论,本问可直接使用)
(3)迁移应用:如图3,在等腰中,,,分别是边,上的点,与相交于点.若,且,求的值.
31.如图,顶点为M的抛物线 与x轴交于A、B两点(点A在点B的左边),与y轴的正半轴交于点C,已知 ,∠ACO=30°
(1)求抛物线的解析式和M的坐标;
(2)若点N是抛物线的对称轴上的一个动点,且满足△CAN是直角三角形,直接写出点N的坐标;
(3)已知点G是y轴上的一点,直接写出GC+2GB的最小值,以及此时点G的坐标.
八、实践探究题
32.
(1)【基本模型】
如图1,已知,线段AC与BD交于点P,且P为线段BD的中点.求证:;
(2)【应用模型】
如图2,在和中,,,且,,将绕点A顺时针方向旋转,把点E在AC边上时的位置作为起始位置(此时点B和点D位于AC的两侧),设旋转角为,连接BD,点P是线段BD的中点,连接PC,PE.当在起始位置时,猜想:PC与PE的数量关系和位置关系,并说明理由;
(3)【拓展迁移】
如图3,在【应用模型】的条件下,当时,点D落在AB边上,请判断PC与PE的数量关系和位置关系,并证明你的结论.
33.综合与实践
如图1,某兴趣小组计划开垦一个面积为的矩形地块种植农作物,地块一边靠墙,另外三边用木栏围住,木栏总长为.
【问题提出】
小组同学提出这样一个问题:若,能否围出矩形地块?
(1)【问题探究】
小颖尝试从“函数图象”的角度解决这个问题:
设为,为.由矩形地块面积为,得到,满足条件的可看成是反比例函数的图象在第一象限内点的坐标;木栏总长为,得到,满足条件的可看成一次函数的图象在第一象限内点的坐标,同时满足这两个条件的就可以看成两个函数图象交点的坐标.
如图2,反比例函数的图象与直线:的交点坐标为和 ,因此,木栏总长为时,能围出矩形地块,分别为:,;或 m, m.
根据小颖的分析思路,完成上面的填空.
(2)【类比探究】
若,能否围出矩形地块?请仿照小颖的方法,在图2中画出一次函数图象并说明理由.
(3)【问题延伸】
当木栏总长为时,小颖建立了一次函数.发现直线可以看成是直线通过平移得到的,在平移过程中,当过点时,直线与反比例函数的图象有唯一交点.
请在图2中画出直线过点时的图象,并求出的值.
(4)【拓展应用】
小颖从以上探究中发现“能否围成矩形地块问题”可以转化为“与图象在第一象限内交点的存在问题”.
若要围出满足条件的矩形地块,且和的长均不小于,请直接写出的取值范围.
答案解析部分
1.【答案】A
【知识点】勾股定理
【解析】【解答】解;∵直角三角形的两条直角边的长为6和8,
∴它的斜边长==10.
故答案为:A.
【分析】利用勾股定理求出斜边的长即可。
2.【答案】D
【知识点】一元二次方程根的判别式及应用
【解析】【解答】解: ∵关于x的一元二次方程有实数根,
∴△=(-2)2-4m≥0,
解得:.
故答案为:D.
【分析】由关于x的一元二次方程有实数根, 可得△≥0,据此解答即可.
3.【答案】B
【知识点】扇形面积的计算;等可能事件的概率
【解析】【解答】解:由题意得,
故答案为:B
【分析】根据扇形的面积公式结合等可能事件的概率即可求解。
4.【答案】B
【知识点】求代数式的值-整体代入求值
【解析】【解答】解: ,将 代入,原式==-3.
故答案为:B.
【分析】先将代数式的分子分母同时除以b,再将代入求值即可.
5.【答案】D
【知识点】二次函数图象与系数的关系;二次函数图象与坐标轴的交点问题;二次函数与不等式(组)的综合应用;二次函数y=ax^2+bx+c的性质
【解析】【解答】解:∵抛物线开口向下,∴a<0.∵对称轴 ,∴b=-4a>0.∵抛物线与y轴交点在y轴正半轴,∴c>0,∴abc<0,故①错误;
由①得:b=-4a,∴4a+b=0,故②正确;
若点A坐标为( 1,0),因为对称轴为x=2,∴B(5,0),∴AB=5+1=6.故③错误;
∵a<0,∴横坐标到对称轴的距离越大,函数值越小.∵0<x1<1,2<x2<3,∴ ,∴y1<y2,故④正确.
故答案为:D.
【分析】根据二次函数的性质判断即可。
6.【答案】A
【知识点】平行线的性质;矩形的判定与性质;翻折变换(折叠问题);锐角三角函数的定义
【解析】【解答】解:如图,过点作,则四边形是矩形,,
四边形是矩形,
,,,
,
,
,
折叠,
∴,
,
,
,
,
,
,
,
,
设,则,
中,,
,
,
,
,
,
,
,
,
.
故答案为:A.
【分析】过点P作PQ⊥BC,则四边形ABQP、QPDC是矩形,PD=QC,根据矩形的性质可得PQ=AB,∠EMP=∠A=90°,EP∥FN,EM∥PF,根据平行线的性质可得∠MPE=∠PNF,根据等角的余角相等可得∠1=∠2,根据折叠的性质可得∠PFE=∠BFE,∠CNG=∠GNP,根据平行线的性质可得∠PEF=∠EFB,∠PGN=∠GNC,推出PE=PF,PG=PN,根据三角函数的概念可设PF=4k,PN=3k,则FN=5k,结合FN的值可得k的值,然后求出PF、PQ、QN、NC、PD、PG,据此计算.
7.【答案】D
【知识点】正方形的性质;相似三角形的判定与性质
【解析】【解答】解:①∵四边形AEFG和四边形ABCD均为正方形
∴∠EAG=∠BAD=90°
又∵∠EAB=90°-∠BAG,∠GAD=90°-∠BAG
∴∠EAB=∠GAD
∴①正确②∵四边形AEFG和四边形ABCD均为正方形
∴AD=DC,AG=FG
∴AC= AD,AF= AG
∴ ,
即
又∵∠DAG+∠GAC=∠FAC+∠GAC
∴∠DAG=∠CAF
∴
∴②正确③∵四边形AEFG和四边形ABCD均为正方形,AF、AC为对角线
∴∠AFH=∠ACF=45°
又∵∠FAH=∠CAF
∴△HAF∽△FAC
∴
即
又∵AF= AE
∴
∴③正确④由②知
又∵四边形ABCD为正方形, AC为对角线
∴∠ADG=∠ACF=45°
∴DG在正方形另外一条对角线上
∴DG⊥AC
∴④正确
故答案为:D.
【分析】根据正方形的性质可得∠EAG=∠BAD=90°,利用同角的余角相等可得∠EAB=∠GAD,据此判断①;根据两组对边成比例且夹角相等,可证,据此判断②;先证△HAF∽△FAC,可得,可得,由AF= AE,即得,据此判断③;由,可得∠ADG=∠ACF=45°,从而求出∠AND=90°,据此判断④.
8.【答案】D
【知识点】三角形全等及其性质;勾股定理;矩形的判定与性质;正方形的性质;相似三角形的判定与性质
【解析】【解答】解:过点K作KP⊥CF,交CF的延长线于点P,DN与CF交于点O,
由题意可知:四边形NMEO和四边形ABCD是正方形,
,,,
,
是等腰三角形,
,
在和中,
,
,
,,
,
,
又,,
,
,
,
,
,
在中,,
,
,
解得:,
,,
,
又,
,
,
∵四边形,
,,
,
,
,,
,
,,
,,
,,
,,
,
,
又,
,
,
在和中,
,
,
,
由题意可得:,
,
,,
,
,
,解得,
,,
,
,
∴四边形是矩形,
,,
由题意可知:,
,
,
,
,
故答案为:D.
【分析】过点K作KP⊥CF,交CF的延长线于点P,DN与CF交于点O,易得四边形NMEO和四边形ABCD是正方形, 首先结合正方形的性质、等腰三角形的性质,可利用HL判断Rt△BAF≌Rt△CDF,得AF=DF,∠AFB=∠DFC,进而借助平行线的性质及等量代换可得∠DAM=∠AFB,由等角对等边得AG=FG,由等角的余角相等得∠BAM=∠ABF,得AG=BG=GF,在Rt△ABF中,利用勾股定理建立方程算出AF,从而可得FD、AB、AD的长,由等面积法求出BE,由勾股定理算出EF,进而判断出△BMG∽△BEF,由相似三角形对应边成比例建立方程可求出MG、BM,利用ASA判断出△KFD≌△GFA得KF=KD=AG=GF,由题意得Rt△BEC≌Rt△DNA,得DN=BE=4,进而再判断出△HNG∽△HDK,由相似三角形对应边成比例建立方程可求出NH,证出四边形PODK是矩形,得PK=DO=2,PO=KD=,由题意得Rt△BEC≌Rt△COD,得OC=BE=4,由勾股定理算出KE,从而即可求出答案.
9.【答案】A,B
【知识点】圆的综合题
【解析】【解答】设则,
∴,,
∵,
∴,
故B符合题意;
∵,,
∴直线不是线段的垂直平分线,
∴,
∴不是等边三角形,
故D不符合题意;
如图,连接,
∵正五边形,,
∴,,,
∴,,,
∴,,,
∴,,
∴,
∴,
故A符合题意;
∵无法计算,
故D不符合题意;
故答案为:A、B.
【分析】利用全等三角形的判定方法和性质,圆的弧、弦及圆周角的关系逐项判断即可。
10.【答案】36
【知识点】解直角三角形的实际应用﹣坡度坡角问题
【解析】【解答】如图:
因为坡度比为1: ,即tanα= ,
∴α=30°.
则其下降的高度=72×sin30°=36米.
故答案为36
【分析】先求出tanα= ,再求出α=30°,最后利用锐角三角函数值计算求解即可。
11.【答案】圆心
【知识点】圆的认识
【解析】【解答】解: 战国时期的《墨经》一书中记载:“圜(圆),一中同长也”,表示圆心到圆上各点的距离都相等,即半径都相等.
故答案为:圆心 .
【分析】 根据圆的几要素,作出判断.
12.【答案】<
【知识点】三角形三边关系;勾股定理
【解析】【解答】解:,,
,
.
故答案为:<.
【分析】利用勾股定理求出AP、BP的长,再比较AP、BP的长,根据三角形中大边对大角即可求解.
13.【答案】29;9
【知识点】定义新运算
【解析】【解答】解:(1)∵6×2+2=14,3×2+3×3=15
∴6233是“凸月数”
∴
故答案为:29
(2)当0≤b<4时
∵s=2640+1000a+100b+10c+d为“凸月数”
∴2(a+2)+(b+6)=14,2(c+4)+3d=15
即2a+b=4,2c+3d=7
∵0≤a≤6,3<b≤9,0≤c≤5,0≤d≤9,其中a、b、c、d均为整数
∴a=1,b=2(或a=2,b=0),c=2,d=1
∴s=3861或4661
当4≤b≤7时
∵s=2640+1000a+100b+10c+d为“凸月数”
∴2(a+3)+(b-4)=14,2(c+4)+3d=15
即2a+b=12,2c+3d=7
∵0≤a≤6,3<b≤9,0≤c≤5,0≤d≤9,其中a、b、c、d均为整数
∴a=3,b=6(或a=4,b=4,),c=2,d=1
∴s=6261或7061
故满足条件s的值为3861或4661或6261或7061
当s=7061时,
故答案为:9
【分析】(1)根据新定义先判断6233为“凸月数”,即可求出答案.
(2)分当0≤b<4时,当4≤b≤7时,根据新定义列出方程,解方程即可求出答案.
14.【答案】
【知识点】勾股定理;平行四边形的判定与性质;相似三角形的判定与性质
【解析】【解答】解:
根据已知可得,OA=2,OB=4,根据勾股定理可得,AB=2
如图,过点C作CE⊥x轴于点E,作CG⊥y轴于点G,过点D作DH⊥x轴于点H,作DF⊥y轴于点F,连接GH,GD,CH
∵点C和点D为反比例函数图象上的点
∴S矩形FDHO=S矩形GCEO
∴S矩形FDHO=S矩形GOEC
∴S△DGH=S△GHC
∴点C,D到GH的距离相等
∴CD∥GH
∴四边形BDHG和四边形GHAC都是平行四边形
∴BD=GH,GH=CA
即BD=AC
设AC=BD=m
∵∠AOC=∠ADO,∠CAO=∠DAO
∴△AOC∽△ADO
∴
∴AO2=AC×AD
∴22=m(2-m)
∴m=+1(舍去),m=-1
过点C作CE⊥x轴于点E
∴△ACE∽△ABO
∴
∴
∴AE=,CE=
∴OE=OA-AE=2-=
∴CE×OE=×=
【分析】如图,过点C作CE⊥x轴于点E,作CG⊥y轴于点G,过点D作DH⊥x轴于点H,作DF⊥y轴于点F,连接GH,GD,CH,根据勾股定理计算得到AB的长度,根据平行四边形的判定和性质以及相似三角形的判定和对应边成比例,计算得到答案即可。
15.【答案】;,,,,
【知识点】定义新运算
【解析】【解答】解:设,
即,
整理得,
故F.
根据题意是一个“六秩数”,且是一个完全平方数,
则满足,且是一个完全平方数,
是一个完全平方数,
故或,
当时,根据进行推算:
,,此时,故,
若,,则,
若,,则,
若,,则,
若,,则,
的最大值与最小值的差为:;
,,此时,故,
若,,则,
若,,舍去,
若,,则,
若,,舍去,
若,,舍去,
若,,舍去,
若,,则,
若,,舍去,
若,,则,
的最大值与最小值的差为:;
,,此时,故,舍去,
,,此时,故
若,,则,
若,,舍去
若,,舍去
若,,舍去
若,,则,
的最大值与最小值的差为:;
,,此时,故,
若,,则,
若,,则,
若,,则,
若,,则,
的最大值与最小值的差为:;
,,此时,故,舍去,
,,此时,故,舍去,
,,此时,故,舍去,
当时,根据进行推算:
,,此时,故,
若,,舍去,
若,,则,
若,,舍去,
若,,则,
若,,舍去,
的最大值与最小值的差为:;
综上,的最大值与最小值的差为:,,,,;
故答案为:;,,,,.
【分析】根据“六秩数”的定义,结合题意计算求解即可。
16.【答案】解:原式
;
【知识点】二次根式的混合运算;实数的混合运算(含开方)
【解析】【分析】先根据0指数幂的性质、二次根式的性质及绝对值的性质分别化简,再合并同类二次根式即可。
17.【答案】解:原式=2+2﹣1=3
【知识点】实数的运算;零指数幂;负整数指数幂
【解析】【分析】首先计算开方,乘方、然后计算乘法,最后从左向右依次计算,求出算式的值是多少即可.
18.【答案】解:原式=6+3×2
=2+18
=24
【知识点】二次根式的混合运算
【解析】【分析】先利用二次根式的乘法法则计算,再计算加法即可.
19.【答案】解:解不等式 ,得: ,
解不等式 ,得: ,
则不等式组的解集为 .
【知识点】解一元一次不等式组
【解析】【分析】分别求出每一个不等式的解集,根据口诀:同大取大、同小取小、大小小大中间找、大大小小找不到确定不等式组的解集.
20.【答案】解:过点P作于点C,设,
由题意可知,
则.
∴在中,
,
∵在中,,
∴,
则,
∴,
∴,
则古树P到公路l的距离约为.
【知识点】解直角三角形的实际应用﹣方向角问题
【解析】【分析】过点P作PC⊥l于点C,设BC=x,根据题意可得到∠PAC=45°,∠PBC=60°,利用解直角三角形表示出PC的长,同时可证得AC=PC,据此可得到关于x的方程,解方程求出x的值,可得到PC的长.
21.【答案】(1)
(2)解:有(1)可知,摸到白球的概率约为1-=,
所以总球数=5=20(个),
所以袋中红球数约为20-5=15(个).
【知识点】利用频率估计概率;概率公式
【解析】【解答】(1)从袋中任意摸出1个球,恰好是红球的概率==;
故答案为:;
【分析】(1)根据用频率估算概率,可以得到摸到红球的概率为;
(2)根据用样本估算总体的定义,可得袋中总的球数;最后根据红球数=总球数-白球的数量,可得红球的数量.
22.【答案】解:(1) 连接PQ,
若=时,PQ//BC,即=,
∴ t=
(2) 过P作PD⊥AC于点D,则有=,
即=,
∴ PD=(5-t)
∴ y=·2t·(5-t)=-+4t(0
AP+AQ=(AB+AC+BC),
即:5-t+2t=6,
∴ t=1
当t=1时,y=3.4;而三角形ABC的面积为6,显然不存在.
过P作PD⊥AC于点D,若QD=CD,则PQ=PC,四边形PQP'C就为菱形.
同(2)方法可求AD=(5-t),所以:
(5-t)-2t=4-(5-t);
解之得:t=.
即t=时,四边形PQP'C为菱形.
【知识点】二次函数的最值;菱形的判定;平行线分线段成比例
【解析】【分析】(1)当PQ∥BC时,我们可得出三角形APQ和三角形ABC相似,那么可得出关于AP,AB,AQ,AC的比例关系,我们观察这四条线段,已知的有AC,根据P,Q的速度,可以用时间t表示出AQ,BP的长,而AB可以用勾股定理求出,这样也就可以表示出AP,那么将这些数值代入比例关系式中,即可得出t的值.
(2)求三角形APQ的面积就要先确定底边和高的值,底边AQ可以根据Q的速度和时间t表示出来.关键是高,可以用AP和∠A的正弦值来求.AP的长可以用AB-BP求得,而sinA就是BC:AB的值,因此表示出AQ和AQ边上的高后,就可以得出y与t的函数关系式.
(3)如果将三角形ABC的周长和面积平分,那么AP+AQ=BP+BC+CQ,那么可以用t表示出CQ,AQ,AP,BP的长,那么可以求出此时t的值,我们可将t的值代入(2)的面积与t的关系式中,求出此时面积是多少,然后看看面积是否是三角形ABC面积的一半,从而判断出是否存在这一时刻.
(4)过点P作PM⊥AC于M,PN⊥BC于N,那么PNCM就是个矩形,解题思路:通过三角形BPN和三角形ABC相似,得出关于BP,PN,AB,AC的比例关系,即可用t表示出PN的长,也就表示出了MC的长,要想使四边形PQP'C是菱形,PQ=PC,根据等腰三角形三线合一的特点,QM=MC,这样有用t表示出的AQ,QM,MC三条线段和AC的长,就可以根据AC=AQ+QM+MC来求出t的值.求出了t就可以得出QM,CM和PM的长,也就能求出菱形的边长了.
23.【答案】(1)解:,
,
(2)证明:如图,将AE绕点A逆时针旋转120°,得到AF,连接CF,EF,过点A作AH⊥EF于H,
∴AE=AF,∠EAF=120°,
∴∠AEF=∠AFE=30°,
∵AH⊥EF,
∴AH=12AE,FH=EH,EH=√3AH,
∴EF=√3AE,
∵∠BAC=∠EAF=120°,
∴∠BAE=∠CAF,
又∵AB=AC,AE=AF,
∴△BAE≌△CAF(SAS),
∴∠BEA=∠AFC,BE=CF,
设∠BEA=∠AFC=x,
∴∠FEC=∠BEC x 30°,
∵2∠BEC ∠AEB=270°,
∴∠BEC=135°+,
∴∠FEC=105° ,
∵∠EFC=∠AFC ∠AFE=x 30°,
∴∠FEC=180° (x 30°) (105 x2)=105° ,
∴∠FEC=∠FCE,
∴EF=CF=BE=AE;
(3)
【知识点】三角形内角和定理;含30°角的直角三角形;旋转的性质;等腰直角三角形;三角形全等的判定(SAS)
【解析】【解答】解:(3)如图,当点P在△ABC内时,将△APC绕点A顺时针旋转120°,得到△AHB,连接HP,
∵∠APB=90°,∠BPC=150°,
∴∠APC=120°,∠PBC+∠PCB=30°,
∴∠ABP+∠ACP=30°,
∵将△APC绕点A顺时针旋转120°,得到△AHB,
∴AP=AH,∠HAP=120°,BH=PC,∠ACP=∠ABH,∠APC=∠AHB=120°,
∴∠AHP=∠APH=30°,∠ABP+∠ABH=30°,
∴∠PHB=90°,∠PBH=30°,
∴BP=2HP,BH=HP,
∴BP=BH=PC,
∴;
如图,当点P在△ABC外时,将△APC绕点A顺时针旋转120°,得到△AHB,连接HP,
∵∠APB=90°,∠BPC=150°,
∴∠APC=60°,∠PBC+∠PCB=30°,
∴∠ABP+∠ACP=90°,
∵将△APC绕点A顺时针旋转120°,得到△AHB,
∴AP=AH,∠HAP=120°,BH=PC,∠ACP=∠ABH,∠APC=∠AHB=60°,
∴∠AHP=∠APH=30°,∠ABP+∠ABH=90°,
∴∠PHB=30°,∠PBH=90°,
∴BH=BP,
∴PC=BP,
∴PCBP=,
综上所述:=或,
故答案为:或.
【分析】(1)由等腰三角形的性质可得∠B=∠C=30°,由角的数量关系可求∠ABC=30°,∠BAD=90°,由直角三角形的性质可得BD=2AD=2CD,即可求解;
(2)将AE绕点A逆时针旋转120°,得到AF,过点A作AH⊥EF于H,由等腰三角形的性质可求EF与AE的数量关系,由“SAS”可证ΔBAE≌ΔCAF,可得∠BEA=∠AFC,BE=CF,由角的数量关系可证∠FEC=∠FCE,可证EF=CF=BE=AE;
(3)分两种情况讨论,由旋转的性质可得AP=AH,∠HAP=120°,BH=PC、∠ACP=∠ABH、∠APC=∠AHB=120°,由直角三角形的性质可求解.
24.【答案】(1)解:如图1所示,连接AP,BP.
∵ 为等边三角形,
∴∠AOB=60°.
∵∠APB= ∠AOB,
∴∠APB=30°.
(2)解:如图2所示:点P在 上即可.
(3)解:由(2)得,要使 的点P恰有两个,则AD与 相交,如图3所示,
①当AD与⊙O相切时,连接OP,并延长PO与BC相交于Q,
∵AD与⊙O相切,
∴∠APQ=90°,
∵四边形ABCD是矩形,
∴∠A=∠ABQ=90°.
∴∠A=∠ABQ=∠APQ=90°.
∴四边形ABQP为矩形,
∴PQ=AB=m.
∵△BOC是等腰直角三角形,
∴OQ= BC= ,OB=2.
∴PQ=2+ .
∴m<2+ .
②当AD与EF重合时,
m=BE=BC=2
综上所述,m的取值范围为:2 ≤m<2+ .
(4)解:如图4所示:
依题意可知,当A,P,O在同一直线上时,AP有最小值,此时PQ最小.
过点O作OH⊥BC于H,作OG⊥AB于G,过点P作PM⊥AB于M,连接OP,OB.
∵∠GBH=90°,
∴四边形BGOH为矩形,
∴OG=BH= BC= .
∵∠BPC=120°,
∴∠BOC=120°,
∵OB=OC,
∴∠OBH=30°.
∴设OH=x,则OB=2x.
在Rt△OBH中
OB2-OH2=BH2,
即4x2-x2=( )2,
解得:x=1.
∴OH=1,OB=2.
∵AB=3,
∴AG=4.
在Rt△AGO中
OA= =
∴AP= -2.
根据旋转的性质可知,AQ=AP= -2,∠PAQ=90°,
根据勾股定理可求得:PQ= = AP= -2 .
∵OG⊥AB,PM⊥AB
∴PM∥OG,
∴ =
∵OG= ,AP= -2,OA=
∴PM= .
∴ 的面积= AB PM= 3 = .
答: 的最小值为 -2 .,并求此时 的面积是 .
【知识点】圆的综合题
【解析】【分析】(1)如图1所示,连接AP,BP.利用等边三角形的性质可得∠AOB=60°,根据圆周角定理可得∠APB= ∠AOB,据此求出结论;
(2)作出正方形BCFE,然后作出其外接圆,点P在 上即可;
(3)由(2)得,要使 的点P恰有两个,则AD与 相交,如图3所示,①当AD与⊙O相切时,连接OP,并延长PO与BC相交于Q,据此求出最大值;②当AD与EF重合时,据此求出最小值;从而求出m的范围;
(4)如图4所示,当A,P,O在同一直线上时,AP有最小值,此时PQ最小.过点O作OH⊥BC于H,作OG⊥AB于G,过点P作PM⊥AB于M,连接OP,OB. 先求出∠OBH=30°,设OH=x,则OB=2x.
在Rt△OBH中,利用勾股定理求出OH=1,OB=2.在Rt△AGO中,利用勾股定理求出OA=,从而可得AP=-2,利用旋转的性质可得AQ=AP= -2,∠PAQ=90°,根据勾股定理可得PQ=AP= -2 . 根据平行线分线段成比例可得 = ,据此求出PM的长,由 的面积= AB PM计算即可.
25.【答案】(1)解:甲同学的画法符合题意.
∵PE∥AD,
∴△MPE~△MNA,
∴ ,
∵EM=2EA,
∴MP:MN=2:3,
∴点P是线段MN的一个三等分点;
(2)解:能画出一个符合题目条件的直线,在EB上取M1,使EM1= AE,直线M1P就是满足条件的直线,如图1;
(3)解:若点P在线段A1C1上,能够画出符合题目条件的直线无数条,如图2;
(4)解:若点P在A1C1,A2C2,B1D1,B2D2上时,可以画出无数条符合条件的直线l;
当点P在正方形A0B0C0D0内部时,不存在这样的直线l,使得点P是线段MN的三等分点;
当点P在矩形ABB1D1,CDD2B2,A0D0D2D1,B0B1B2C0内部时,过点P可画出两条符合条件的直线l,使得点P是线段MN的三等分点.
【知识点】正方形的性质;相似三角形的判定与性质
【解析】【分析】(1)利用△MPE∽△MNA中的成比例线段可知EM=2EA,所以MP:MN=2:3,即点P是线段MN的一个三等分点;(2)由(1)中的证明过程可知,在EB上取M1,使EM1= AE,直线M1P就是满足条件的直线,所以能画出一条符合题目条件的直线;(3)当点P在线段A1C1上,根据正方形的性质可知能够画出符合题目条件的直线有无数条;(4)分情况讨论.
26.【答案】(1)证明:∵ 平分 , ,
∴ ,
∵AF=AF,
∴△AFE≌△AFC(ASA),
∴ ;
(2)解:由(1)可得△AFE≌△AFC,
∴∠AEC=∠ACE,
∵ , ,
∴∠AEC=∠ACE=40°,
∴ .
【知识点】垂线;三角形的外角性质;三角形全等的判定(ASA);角平分线的定义
【解析】【分析】(1)由角平分线易得 ,根据 可得 ,易证 △AFE≌△AFC 可得结果;
(2)由 , 可得 ∠ACE=40°, 由(1)可得 ∠AEC=∠ACE ,根据三角形外角性质可得结果.
27.【答案】(1)解:列表得:
第一次 第二次 1 2 3 4
1 (1,1) (2,1) (3,1) (4,1)
2 (1,2) (2,2) (3,2) (4,2)
3 (1,3) (2,3) (3,3) (4,3)
4 (1,4) (2,4) (3,4) (4,4)
则共有16种等可能的结果;
(2)解:∵这样的点落在如图所示的圆内的有:(1,1),(1,2),(1,3),(2,1),(2,2),(2,3),(3,1),(3,2),(3,3),
∴这样的点落在如图所示的圆内的概率为:
【知识点】列表法与树状图法
【解析】【分析】(1)首先根据题意列出表格,然后由表格即可求得所有等可能的结果;(2)根据(1)中的表格求得这样的点落在如图所示的圆内的情况,然后利用概率公式求解即可求得答案.
28.【答案】(1)解:设每次上涨的百分率为x,根据题意得:
,
解得:(不合题意,舍去),
答:每次上涨的百分率为;
(2)解:根据题意得:
∴当m=20时,W最大,最大值为2000,
答:当降价钱数m为20元时,每天的利润W可达到最大,最大利润是2000元.
【知识点】一元二次方程的实际应用-百分率问题;二次函数的实际应用-销售问题
【解析】【分析】(1)设每次上涨的百分率为x,根据题意列出方程,再求解即可;
(2)根据题意列出函数解析式,再利用二次函数的性质求解即可。
29.【答案】(1)证明:∵是的中点,
∴,
∵,
∴,
又∵,
∴,
∴,
∵,是的中点,
∴,
∴四边形为平行四边形,
又∵,
∴平行四边形为菱形;
(2)解:,
由题意可得:,
【知识点】菱形的判定;几何图形的面积计算-割补法
【解析】【分析】(1)先证明四边形为平行四边形,再结合AD=CD,可得平行四边形为菱形;
(2)利用割补法求出即可。
30.【答案】(1);
(2)证明:∵,,
∴是等边三角形,
∴,.
∵在等边中,,,
∴,
∴,
∴,
∴,
∴,
∴平分.
(3)解:如图,延长至,使得,连接,,过点作,交于点.
设.
∵,,
∴,
∴,
∴,
∴.
∵,即,
∴,
∴,,
∴,.
∵,
∴,
∴,,
∴.
【知识点】三角形的外角性质;等边三角形的判定与性质;相似三角形的判定与性质;三角形全等的判定(SAS)
【解析】【解答】(1)解:∵是等边三角形,
∴,
∵,
∴,
∴,
∴;
故答案为:;
【分析】(1)根据SAS证明△ABE≌△CAD,可得AD=BE,∠ABE=∠CAD,根据三角形的外角的性质可得;
(2)根据SAS证明△ABF≌△CBG,可得, 根据角的和差求出∠CGA=60°,根据角平分线的定义即得结论;
(3) 延长至,使得,连接,,过点作,交于点. 根据两边成比例且夹角相等可证,可得,再证, 可得 , ∠CHA=∠BHG,利用平行线的性质可得, 从而得出,, 从而得出.
31.【答案】(1)解:根据题意,当 时,
∴ ,即
∵
∴
∵
∴
∴
又∵
∴
∴
∴
∴抛物线对称轴为:
当 时,
∴ ;
(2) 或 或 ;
(3)GC+2GB的最小值 ,
【知识点】线段的性质:两点之间线段最短;含30°角的直角三角形;勾股定理的逆定理;锐角三角函数的定义
【解析】【解答】解:(2)解:点N是抛物线的对称轴上的一个动点,设点N的坐标为:
根据题意得:
根据题意,△CAN是直角三角形,分 、 、 三种情况分析;
第一种情况, ,如下图:
∴
∴
∴
∴
第二种情况, ,如下图:
∴
∴
∴
∴
∴ ;
第三种情况, ,如下图:
∴
∴
∴
∴
∴ ;
∴ 或 或 ;
(3)∵
当 , 或
∵点A在点B的左边
∴
∴
∴
如图,连接GB,过点G做 交AC于点Q
∵∠ACO=30°
∴ ,∠CAO=60°
如下图,连接BQ,BQ交y轴于点P
当点G和点P重合时, 最短,即
∴ 最小值为:
如图,点G和点P重合,此时 交AC于点Q
∵∠CAO=60°,
∴
∴
∴ ,即 最小值为
∵∠CAO=60°
∴
∴
∴
∴ .
【分析】 (1)根据点A的坐标,再直角三角形含30°角的性质利用三角函数求出OC长,确定C的坐标可得n=2,再将点A的坐标代入抛物线的解析式,再配方即可求得顶点M的坐标;
(2)设N(1,n),根据两点的距离公式求得AC为16,CN2=12+(n-2)2,
AN2=(1+2)2+n2=9+n2,当△CAN是直角三角形时,分三种情况,根据勾股定理列方程求解即可;
(3)根据( 1)的结论,首先计算得OB、AB;连接GB,过点G做GQ⊥AC交AC于点Q,根据三角函数性质得QG=GC;再根据两点之间线段最短的性质,得GC+GB最小值为:QB;再根据三角函数的性质计算即可得到结果.
32.【答案】(1)证明:
∵,
∴,
∵点P为BD中点,
∴
在和中,
∴(ASA)
(2)解:,,理由如下:
如图2,延长EP交BC于F,
∵,
∴,
∴,
∵点P是线段BD的中点,
∴,
又∵,
∴(ASA),
∴,,
又∵,,
∴,
又∵,
∴是等腰直角三角形,
∵,
∴,;
(3)解:,,理由如下:
如图3,过点B作,交EP延长线于点F,连接CE,CF,
同理(2)可证,
∴,,
∵,
∴,
∵当时,,
∴,,
∵,
∴,
∴,
∴,
在和中,
∴(SAS)
∴,,
∴
∴
∴是等腰直角三角形,
∵,
∴,
【知识点】旋转的性质;三角形全等的判定(ASA);三角形的综合
【解析】【分析】(1)利用“ASA”证明即可;
(2)先证明是等腰直角三角形,再结合EP=FP可得,;
(3)先利用“SAS”证明可得 ,, 再证明 是等腰直角三角形, 结合EP=FP可得 , 。
33.【答案】(1);4;2
(2)解:不能围出.
∵木栏总长为,
∴,则,
画出直线的图象,如图中所示:
∵与函数图象没有交点,
∴不能围出面积为的矩形;
(3)解:如图中直线所示,即为图象,
将点代入,得:,
解得;
(4)解:根据题意可得∶ 若要围出满足条件的矩形地块, 与图象在第一象限内交点的存在问题,
即方程有实数根,
整理得:,
∴,
解得:,
把代入得:,
∴反比例函数图象经过点,
把代入得:,解得:,
∴反比例函数图象经过点,
令,,过点,分别作直线的平行线,
由图可知,当与图象在点A左边,点B右边存在交点时,满足题意;
把代入得:,
解得:,
∴.
【知识点】一元二次方程根的判别式及应用;一次函数的图象;待定系数法求反比例函数解析式
【解析】【解答】解:(1)∵反比例函数,直线:,
∴联立可得方程组:,
解得:,,
∴反比例函数的图象与直线:的交点坐标为和 (4,2);
∴木栏总长为时,能围出矩形地块,分别为:,;或 4m,BC=2m,
故答案为:(4,2);4;2.
【分析】(1)根据题意先求出方程组:,再求出,,最后求解即可;
(2)根据题意先求出 , 再根据 与函数图象没有交点, 计算求解即可;
(3)将点代入,求出, 最后作图求解即可;
(4)利用一元二次方程根的判别式求出 , 再利用待定系数法求出 反比例函数图象经过点, 最后列方程计算求解即可。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
