广东省惠州市惠阳区第一中学2023-2024学年九年级下学期第一次月考数学试题(无答案)
文档属性
| 名称 | 广东省惠州市惠阳区第一中学2023-2024学年九年级下学期第一次月考数学试题(无答案) |  | |
| 格式 | docx | ||
| 文件大小 | 385.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-04-16 22:53:12 | ||
图片预览

文档简介
惠阳区第一中学2024年九年级第二学期第一次月考
(考试时间:120分钟 试卷满分:120分)
选择题(本大题共10小题,每小题3分,共30分,每小题有四个选项,其中只有一个是正确的)。
下列几何体中,主视图为三角形的是( )
2. 0.5的倒数是( )
A.5 B.2 C.-0.5 D.-2
3. 要使分数有意义,则x的取值范围是( )
A. x=1 B. x>1 C. x<1 D. x≠1
4. 下列计算正确的是( )
A. B. C. D.
5. 若反比例函数的图象经过点(1,-3),则它的图象也一定经过的点是( )
A.(-3,1) B.(-1,-3) C.(-3,-1) D.(1,3)
6. 把一元二次方程化成的形式,问转化后的二次项系数、一次项系数、常数项分别为( )
A.3,-2,1 B.-3,2,-1 C.3,-2,-1 D.3,2,-1
7. 如图,小手盖住的点的坐标可能是( )
A.(-3,-3) B.(2,3) C.(2,-5) D.(-3,4)
8. 如图,若在棋盘上建立平面直角坐标系,使“帅”位于点(2,0),“炮”位于点(-1,3)。则将棋子“马”向上平移两个单位长度后位于点( )
A.(4,2) B.(4,1) C.(4,4) D.(6,2)
9. 在解方程时,去分母正确的是( )
A. B.
C. D.
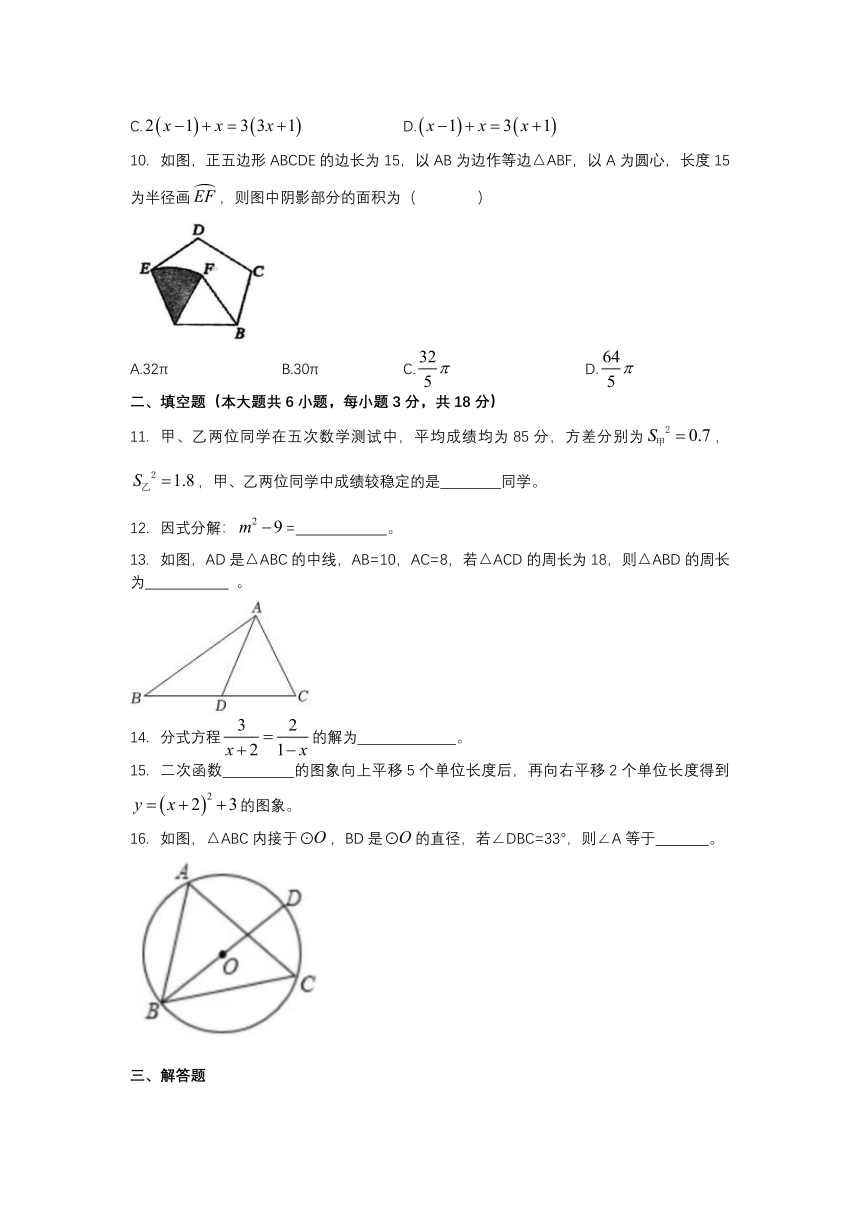
10. 如图,正五边形ABCDE的边长为15,以AB为边作等边△ABF,以A为圆心,长度15为半径画,则图中阴影部分的面积为( )
A.32π B.30π C. D.
二、填空题(本大题共6小题,每小题3分,共18分)
11. 甲、乙两位同学在五次数学测试中,平均成绩均为85分,方差分别为,,甲、乙两位同学中成绩较稳定的是 同学。
12. 因式分解:= 。
13. 如图,AD是△ABC的中线,AB=10,AC=8,若△ACD的周长为18,则△ABD的周长为 。
14. 分式方程的解为 。
15. 二次函数 的图象向上平移5个单位长度后,再向右平移2个单位长度得到的图象。
16. 如图,△ABC内接于,BD是的直径,若∠DBC=33°,则∠A等于 。
三、解答题
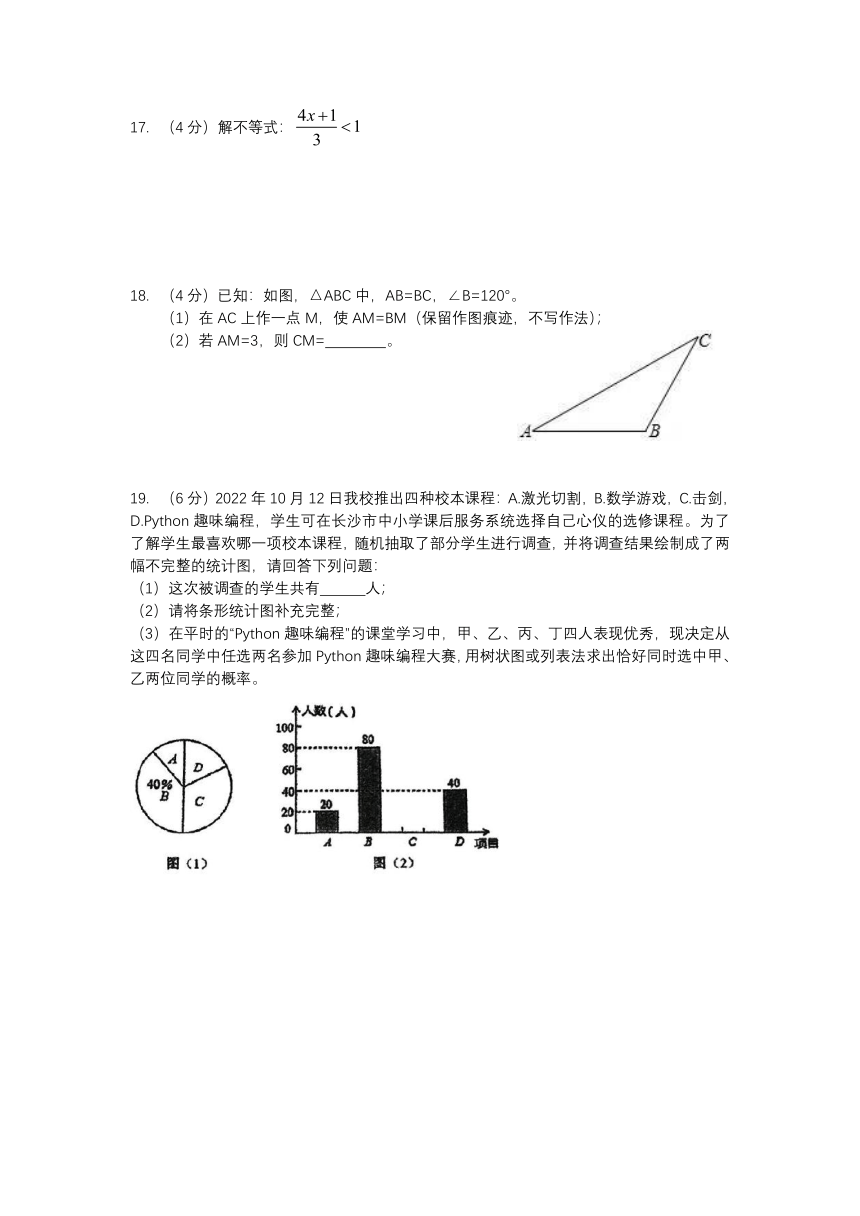
17. (4分)解不等式:
18. (4分)已知:如图,△ABC中,AB=BC,∠B=120°。
(1)在AC上作一点M,使AM=BM(保留作图痕迹,不写作法);
(2)若AM=3,则CM= 。
19. (6分)2022年10月12日我校推出四种校本课程:A.激光切割,B.数学游戏,C.击剑,D.Python趣味编程,学生可在长沙市中小学课后服务系统选择自己心仪的选修课程。为了了解学生最喜欢哪一项校本课程,随机抽取了部分学生进行调查,并将调查结果绘制成了两幅不完整的统计图,请回答下列问题:
(1)这次被调查的学生共有 人;
(2)请将条形统计图补充完整;
(3)在平时的“Python趣味编程”的课堂学习中,甲、乙、丙、丁四人表现优秀,现决定从这四名同学中任选两名参加Python趣味编程大赛,用树状图或列表法求出恰好同时选中甲、乙两位同学的概率。
20. (6分)如图是从正面、左面、上面看到的几何体的形状图。
(1)该几何体的名称
(2)根据图中所示数据求得这个几何体的表面积是多少?(保留π)
21. (8分)已知。
(1)化简P;
(2)若某圆锥的底面半径为a,母线长为b,且侧面积为2π,求P的值。
22. (10分)如图,在△ABC中,AB=AC,AE是BC边上的高线,BM平分∠ABC交AE于点M,经过B,M两点的交BC于点G,交AB于点F,FB为的直径。
(1)求证:AM是的切线;
(2)当CE=3,cosC=时,求的半径。
23. (10分)西岗区某中学为落实《教育部办公厅关于进一步加强中小学生体质管理的通知》文件要求,决定增设篮球、足球两门选修课程,为此需要购进一批篮球和足球。已知购买2个篮球和3个足球需要510元;购买3个篮球和5个足球需要810元。
(1)根据以上信息解答若需要购买1个篮球和2个足球需要多少钱?
(2)学校计划采购篮球、足球共50个,并要求篮球不少于30个,且总费用不超过5500元,则有哪几种购买方案?
24. (12分)如图,△ABC内接于,AB是直径,过点A作直线MN,且MN是的切线。
(1)求证:∠MAC=∠ABC。
(2)设D是弧AC的中点,连接BD交AC于点G,过点D作DE⊥AB于点E,交AC于点F。
①求证:FD=FG;
②若BC=3,AB=5,试求AE的长。
25 (12分)如图,已知抛物线经过点A(-3,0),B(1,0),与y轴交于点C。
(1)求抛物线的解析式;
(2)若点P为该抛物线上一点,且点P的横坐标为m。
①当点P在直线AC下方时,过点P作PE∥x轴,交直线AC于点E,作PF∥y轴。交直线AC于点F,求PE+PF的最大值;
②若∠PCB=3∠OCB,求m的值。
(考试时间:120分钟 试卷满分:120分)
选择题(本大题共10小题,每小题3分,共30分,每小题有四个选项,其中只有一个是正确的)。
下列几何体中,主视图为三角形的是( )
2. 0.5的倒数是( )
A.5 B.2 C.-0.5 D.-2
3. 要使分数有意义,则x的取值范围是( )
A. x=1 B. x>1 C. x<1 D. x≠1
4. 下列计算正确的是( )
A. B. C. D.
5. 若反比例函数的图象经过点(1,-3),则它的图象也一定经过的点是( )
A.(-3,1) B.(-1,-3) C.(-3,-1) D.(1,3)
6. 把一元二次方程化成的形式,问转化后的二次项系数、一次项系数、常数项分别为( )
A.3,-2,1 B.-3,2,-1 C.3,-2,-1 D.3,2,-1
7. 如图,小手盖住的点的坐标可能是( )
A.(-3,-3) B.(2,3) C.(2,-5) D.(-3,4)
8. 如图,若在棋盘上建立平面直角坐标系,使“帅”位于点(2,0),“炮”位于点(-1,3)。则将棋子“马”向上平移两个单位长度后位于点( )
A.(4,2) B.(4,1) C.(4,4) D.(6,2)
9. 在解方程时,去分母正确的是( )
A. B.
C. D.
10. 如图,正五边形ABCDE的边长为15,以AB为边作等边△ABF,以A为圆心,长度15为半径画,则图中阴影部分的面积为( )
A.32π B.30π C. D.
二、填空题(本大题共6小题,每小题3分,共18分)
11. 甲、乙两位同学在五次数学测试中,平均成绩均为85分,方差分别为,,甲、乙两位同学中成绩较稳定的是 同学。
12. 因式分解:= 。
13. 如图,AD是△ABC的中线,AB=10,AC=8,若△ACD的周长为18,则△ABD的周长为 。
14. 分式方程的解为 。
15. 二次函数 的图象向上平移5个单位长度后,再向右平移2个单位长度得到的图象。
16. 如图,△ABC内接于,BD是的直径,若∠DBC=33°,则∠A等于 。
三、解答题
17. (4分)解不等式:
18. (4分)已知:如图,△ABC中,AB=BC,∠B=120°。
(1)在AC上作一点M,使AM=BM(保留作图痕迹,不写作法);
(2)若AM=3,则CM= 。
19. (6分)2022年10月12日我校推出四种校本课程:A.激光切割,B.数学游戏,C.击剑,D.Python趣味编程,学生可在长沙市中小学课后服务系统选择自己心仪的选修课程。为了了解学生最喜欢哪一项校本课程,随机抽取了部分学生进行调查,并将调查结果绘制成了两幅不完整的统计图,请回答下列问题:
(1)这次被调查的学生共有 人;
(2)请将条形统计图补充完整;
(3)在平时的“Python趣味编程”的课堂学习中,甲、乙、丙、丁四人表现优秀,现决定从这四名同学中任选两名参加Python趣味编程大赛,用树状图或列表法求出恰好同时选中甲、乙两位同学的概率。
20. (6分)如图是从正面、左面、上面看到的几何体的形状图。
(1)该几何体的名称
(2)根据图中所示数据求得这个几何体的表面积是多少?(保留π)
21. (8分)已知。
(1)化简P;
(2)若某圆锥的底面半径为a,母线长为b,且侧面积为2π,求P的值。
22. (10分)如图,在△ABC中,AB=AC,AE是BC边上的高线,BM平分∠ABC交AE于点M,经过B,M两点的交BC于点G,交AB于点F,FB为的直径。
(1)求证:AM是的切线;
(2)当CE=3,cosC=时,求的半径。
23. (10分)西岗区某中学为落实《教育部办公厅关于进一步加强中小学生体质管理的通知》文件要求,决定增设篮球、足球两门选修课程,为此需要购进一批篮球和足球。已知购买2个篮球和3个足球需要510元;购买3个篮球和5个足球需要810元。
(1)根据以上信息解答若需要购买1个篮球和2个足球需要多少钱?
(2)学校计划采购篮球、足球共50个,并要求篮球不少于30个,且总费用不超过5500元,则有哪几种购买方案?
24. (12分)如图,△ABC内接于,AB是直径,过点A作直线MN,且MN是的切线。
(1)求证:∠MAC=∠ABC。
(2)设D是弧AC的中点,连接BD交AC于点G,过点D作DE⊥AB于点E,交AC于点F。
①求证:FD=FG;
②若BC=3,AB=5,试求AE的长。
25 (12分)如图,已知抛物线经过点A(-3,0),B(1,0),与y轴交于点C。
(1)求抛物线的解析式;
(2)若点P为该抛物线上一点,且点P的横坐标为m。
①当点P在直线AC下方时,过点P作PE∥x轴,交直线AC于点E,作PF∥y轴。交直线AC于点F,求PE+PF的最大值;
②若∠PCB=3∠OCB,求m的值。
同课章节目录
