4.3公式法第2课时(同步课件) 课件(共24张PPT)-八年级数学下册同步精品课堂(北师大版)
文档属性
| 名称 | 4.3公式法第2课时(同步课件) 课件(共24张PPT)-八年级数学下册同步精品课堂(北师大版) |

|
|
| 格式 | pptx | ||
| 文件大小 | 337.1KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-04-17 21:15:43 | ||
图片预览







文档简介
(共24张PPT)
北师大版 数学 八年级下册
第2课时
第四章 因式分解
3 公式法
学习目标
1.理解并掌握用完全平方公式分解因式.(重点)
2.灵活应用各种方法分解因式,并能利用因式分解进行计算.
(难点)
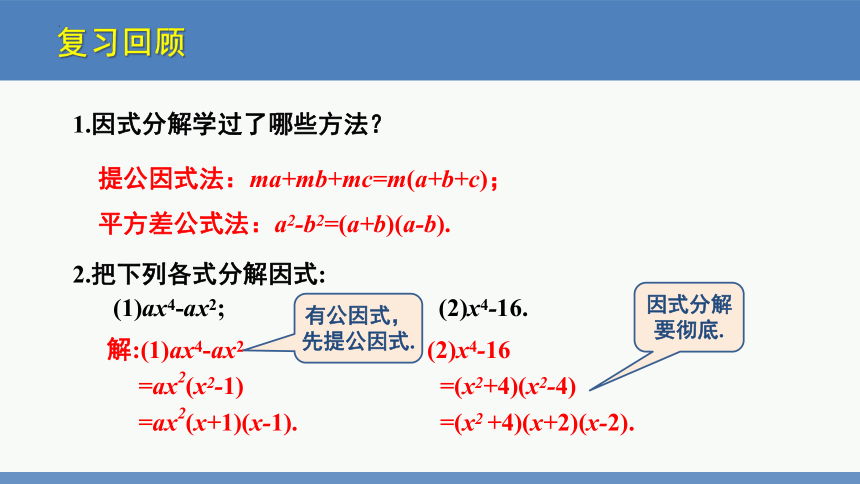
2.把下列各式分解因式:
(1)ax4-ax2; (2)x4-16.
复习回顾
提公因式法:ma+mb+mc=m(a+b+c);
平方差公式法:a2-b2=(a+b)(a-b).
解:(1)ax4-ax2
=ax2(x2-1)
=ax2(x+1)(x-1).
(2)x4-16
=(x2+4)(x2-4)
=(x2 +4)(x+2)(x-2).
1.因式分解学过了哪些方法?
有公因式,先提公因式.
因式分解要彻底.
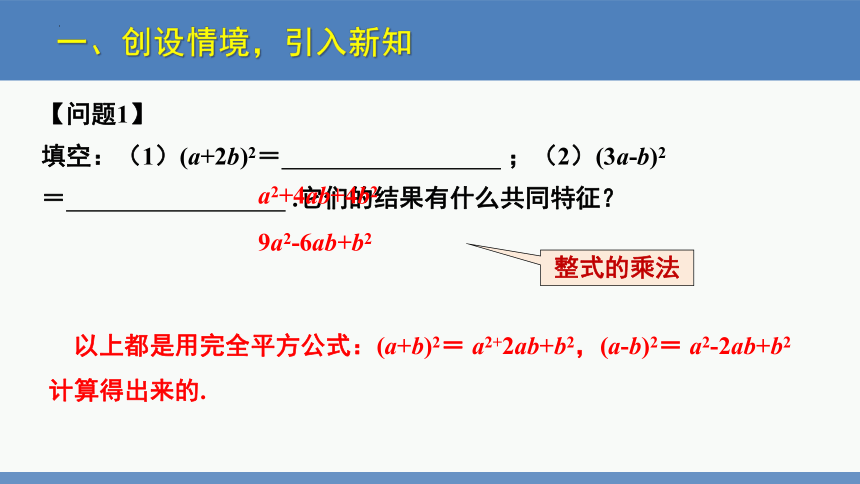
一、创设情境,引入新知
【问题1】
填空:(1)(a+2b)2= ;(2)(3a-b)2 = .它们的结果有什么共同特征?
a2+4ab+4b2
9a2-6ab+b2
以上都是用完全平方公式:(a+b)2= a2+2ab+b2,(a-b)2= a2-2ab+b2计算得出来的.
整式的乘法
一、创设情境,引入新知
【问题2】根据问题1中等式填空:(1)a2+4ab+4b2= ;(2)9a2-6ab+b2= .
(a+2b)2
(3a-b)2
思考:根据学方差公式因式分解的经验和方法,你能将形如“a2+2ab+b2、a2-2ab+b2”的式子因式分解吗?
因式分解
它们有什么共同特征?你能由此得到什么结论?
二、自主合作,探究新知
探究一:用完全平方公式因式分解
将完全平方公式(a+b)2= a2+2ab+b2, (a-b)2 =a2-2ab+b2反过来,就得到:
语言叙述:两个数的平方和加上(或减去)这两个数的积的2倍,等于这两个数的和(或差)的平方.
形如 a2±2ab+b2的式子称为完全平放式.
因式分解的完全平方公式:
a2+2ab+b2=(a+b)2 , a2-2ab+b2=(a-b)2 .
二、自主合作,探究新知
议一议:下列各式是不是完全平方式?
(1)a2-4a+4; (2)1+4a ;
(3)4b2+4b-1; (4)a2+ab+b2;
(5)x2+x+0.25.
是
(2)因为它只有两项;
不是
(3)4b 与-1的符号不统一;
不是
分析:
不是
是
(4)因为ab不是a与b的积的2倍.
二、自主合作,探究新知
完全平放式的特点:
1.是三项式(或可以看成三项);
2.有两个同号的数或式的平方;
3.中间是这两个数的积的±2倍.
只有完全平放式才可以用完全平方公式因式分解.
知识要点
注意:公式中的a,b既可以是单项式,也可以是多项式.
例1:下列多项式能用完全平方公式分解因式的有( )(1)a2+ab+b2;(2)a2-a+;(3)9a2-24ab+4b2;(4)-a2+8a-16.
A.1个 B.2个 C.3个 D.4个
二、自主合作,探究新知
典型例题
B
解析:(1)a2+ab+b2,乘积项不是两数的2倍,不能运用完全平方公式;(2)a2-a+=(a-)2;(3)9a2-24ab+4b2,乘积项是这两数的4倍,不能用完全平方公式;(4)-a2+8a-16=-(a2-8a+16)=-(a-4)2.所以(2)(4)能用完全平方公式分解.
二、自主合作,探究新知
做一做:把下列完全平方式因式分解:
(1)x2+14x+49; (2)(m+n)2-6(m+n)+9.
解:(1)x2+14x+49
= x2+2×7x+72
= (x+7) 2 ;
(2)(m+n)2-6(m+n)+9
= [(m+n)-3]2
=(m+n-3)2.
根据因式分解与整式乘法的关系,我们可以利用乘法公式把某些多项式因式分解,这种因式分解的方法叫做公式法.
二、自主合作,探究新知
归纳:因式分解前应先分析多项式的特点,一般先提公因式,再套用公式.分解因式必须进行到每一个多项式都不能再分解因式为止.
典型例题
例2 把下列各式因式分解:
(1)3ax2+6axy+3ay2; (2)-x2-4y2+4xy.
解:(1)3ax2+6axy+3ay2
= 3a(x2+2xy+y2)
=3a(x+y)2;
(2)-x2-4y2+4xy
= -(x2+4y2-4xy)
= -(x2-4xy+4y2)
=-[x2-2·x·2y+(2y)2]
= -(x-2y)2.
二、自主合作,探究新知
做一做:计算或化简下列各式:(1)2022+202×196+982; (2)(a2-2)2-2a2(a2-2)+a4.
探究二:平方差公式因式分解的应用
解:(1) 2022+202×196+982
=2022+2×202×98+982
=(202+98)2
=3002
=90 000.
(2) (a2-2)2-2a2(a2-2)+a4
=(a2-2)2-2a2(a2-2)+(a2)2
=(a2-2-a2)2
=(-2)2
=4.
利用完全平方公式因式分解,可以简化计算.
二、自主合作,探究新知
例3:已知a,b,c分别是△ABC三边的长,且a2+2b2+c2-2b(a+c)=0,请判断△ABC的形状,并说明理由.
∴△ABC是等边三角形.
解:由a2+2b2+c2-2b(a+c)=0,得
a2-2ab+b2+b2-2bc+c2=0,
即(a-b)2+(b-c)2=0,
∴a-b=0,b-c=0,
∴a=b=c,
典型例题
2.因式分解x2-2x+1的最终结果是( )A.x(x-2)+1 B.(x+1)(x-2)C.(x-1)2 D.(x+1)2
1.下列各式中能用完全平方公式进行因式分解的是( )
A.x2+x+1 B.x2+2x-1
C.x2-1 D.x2-6x+9
三、即学即练,应用知识
C
D
3.计算1002-2×100×99+992的值为( )A.0 B.1
C.-1 D.39601
B
5.已知9x2-mxy+16y2能运用完全平方公式因式分解,则m的值为( )A.12 B.±12
C.24 D.±24
4.把多项式8a3-8a2+2a因式分解,结果正确的是( )A.2a(4a2-4a+1) B.8a2(a-1)C.2a(2a-1)2 D.2a(2a+1)2
三、即学即练,应用知识
C
D
7.因式分解:2m2-12m+18= .
三、即学即练,应用知识
6.下列各式中,能用完全平方公式进行因式分解的是 .(填序号)①x2-2x-2;②x2+1;③x2-4x+4;④x2+4x+1.
③
2(m-3)2
8.若m=2n+1,则m2-4mn+4n2的值是________.
1
三、即学即练,应用知识
9.把下列各式因式分解:(1)-x2+2x-1; (2)9(a-b)2+42(a-b)+49;
(3)x3-2x2y+xy2; (4)x2(y2-1)+2x(y2-1)+(y2-1).
解: (1)-x2+2x-1
=-(x2-2x+1)
=-(x-1)2.
(2)9(a-b)2+42(a-b)+49
=[3(a-b)+7]2
=(3a-3b+7)2;
(3)x3-2x2y+xy2
=x(x2-2xy+y2)
=x(x-y)2;
(4)x2(y2-1)+2x(y2-1)+(y2-1)
=(x2+2x+1)(y2-1)
=(x+1)2(y+1)(y-1).
四、课堂小结
a2±2ab+b2=(a±b)2
公式法2
完全平方公式因式分解
公式法
语言叙述:两个数的平方和加上(或减去)这两个数的积的2倍,等于这两个数的和(或差)的平方.
完全平放式的特点:
1.是三项式(或可以看成三项);
2.有两个同号的数或式的平方;
3.中间是这两个数的积的±2倍.
根据因式分解与整式乘法的关系,我们可以利用乘法公式把某些多项式因式分解,这种因式分解的方法叫做公式法.
2.小华同学利用完全平方公式对下列式子进行因式分解,你认为正确的是( )A.x2+4x+4=(x+4)2B.4x2-2x+1=(2x-1)2C.9-6(m-n)+(m-n)2=(3-m-n)2D.-a2-b2+2ab=-(a-b)2
五、当堂达标检测
D
1.下列四个多项式中,能因式分解的是( )
A.a2+1 B.a2-6a+9
C.x2+5y D.x2-5y
B
五、当堂达标检测
3.把多项式4x2y-4xy2-x3分解因式的结果是( )
A.4xy(x-y)-x3 B.-x(x-2y)2
C.x(4xy-4y2-x2) D.-x(-4xy+4y2+x2)
B
4.计算:1252-50×125+252=( )
A.100 B.150
C.10 000 D.22 500
C
7.如图所示,是长与宽分别为a,b的长方形,它的周长为14,面积为10,则a3b+2a2b2+ab3的值为________.
5.因式分解(a-b)2+4ab的结果是 .
五、当堂达标检测
6.若关于x的多项式x2-8x+m2是完全平方式,则m的值为________.
±4
(a+b)2
490
五、当堂达标检测
8.把下列多项式因式分解.
(1)x2-12x+36; (2)2a2b-a3-ab2;
(3)4(2a+b)2-4(2a+b)+1; (4) y2+2y+1-x2;
(3)4(2a+b)2-4(2a+b)+1
=[2(2a+b)] - 2·2(2a+b)·1+(1)
=(4a+2b - 1)2;
解:(1)x2-12x+36
=x2-2·x·6+(6)2
=(x-6)2;
(4)y2+2y+1-x2
=(y+1) -x
=(y+1+x)(y+1-x).
(2)2a2b-a3-ab2
=-a(a2-2ab+b2)
=-a(a-b)2;
五、当堂达标检测
9.阅读材料:在因式分解中,有一类形如x2+(m+n)x+mn的多项式,其常数项是两个因数的积,而它的一次项系数恰是这两个因数的和,则我们可以把它分解:x2+(m+n)x+mn=(x+m)(x+n).例如:x2+5x+6=x2+(2+3)x+2×3=(x+2)·(x+3).运用上述方法因式分解:(1)x2+6x+8; (2)x2-x-6; (3)x2-5xy+6y2.
解: (1)x2+6x+8=(x+2)(x+4);
(2)x2-x-6=(x+2)(x-3);
(3)x2-5xy+6y2=(x-2y)(x-3y).
教材习题4.5.
六、布置作业
北师大版 数学 八年级下册
第2课时
第四章 因式分解
3 公式法
学习目标
1.理解并掌握用完全平方公式分解因式.(重点)
2.灵活应用各种方法分解因式,并能利用因式分解进行计算.
(难点)
2.把下列各式分解因式:
(1)ax4-ax2; (2)x4-16.
复习回顾
提公因式法:ma+mb+mc=m(a+b+c);
平方差公式法:a2-b2=(a+b)(a-b).
解:(1)ax4-ax2
=ax2(x2-1)
=ax2(x+1)(x-1).
(2)x4-16
=(x2+4)(x2-4)
=(x2 +4)(x+2)(x-2).
1.因式分解学过了哪些方法?
有公因式,先提公因式.
因式分解要彻底.
一、创设情境,引入新知
【问题1】
填空:(1)(a+2b)2= ;(2)(3a-b)2 = .它们的结果有什么共同特征?
a2+4ab+4b2
9a2-6ab+b2
以上都是用完全平方公式:(a+b)2= a2+2ab+b2,(a-b)2= a2-2ab+b2计算得出来的.
整式的乘法
一、创设情境,引入新知
【问题2】根据问题1中等式填空:(1)a2+4ab+4b2= ;(2)9a2-6ab+b2= .
(a+2b)2
(3a-b)2
思考:根据学方差公式因式分解的经验和方法,你能将形如“a2+2ab+b2、a2-2ab+b2”的式子因式分解吗?
因式分解
它们有什么共同特征?你能由此得到什么结论?
二、自主合作,探究新知
探究一:用完全平方公式因式分解
将完全平方公式(a+b)2= a2+2ab+b2, (a-b)2 =a2-2ab+b2反过来,就得到:
语言叙述:两个数的平方和加上(或减去)这两个数的积的2倍,等于这两个数的和(或差)的平方.
形如 a2±2ab+b2的式子称为完全平放式.
因式分解的完全平方公式:
a2+2ab+b2=(a+b)2 , a2-2ab+b2=(a-b)2 .
二、自主合作,探究新知
议一议:下列各式是不是完全平方式?
(1)a2-4a+4; (2)1+4a ;
(3)4b2+4b-1; (4)a2+ab+b2;
(5)x2+x+0.25.
是
(2)因为它只有两项;
不是
(3)4b 与-1的符号不统一;
不是
分析:
不是
是
(4)因为ab不是a与b的积的2倍.
二、自主合作,探究新知
完全平放式的特点:
1.是三项式(或可以看成三项);
2.有两个同号的数或式的平方;
3.中间是这两个数的积的±2倍.
只有完全平放式才可以用完全平方公式因式分解.
知识要点
注意:公式中的a,b既可以是单项式,也可以是多项式.
例1:下列多项式能用完全平方公式分解因式的有( )(1)a2+ab+b2;(2)a2-a+;(3)9a2-24ab+4b2;(4)-a2+8a-16.
A.1个 B.2个 C.3个 D.4个
二、自主合作,探究新知
典型例题
B
解析:(1)a2+ab+b2,乘积项不是两数的2倍,不能运用完全平方公式;(2)a2-a+=(a-)2;(3)9a2-24ab+4b2,乘积项是这两数的4倍,不能用完全平方公式;(4)-a2+8a-16=-(a2-8a+16)=-(a-4)2.所以(2)(4)能用完全平方公式分解.
二、自主合作,探究新知
做一做:把下列完全平方式因式分解:
(1)x2+14x+49; (2)(m+n)2-6(m+n)+9.
解:(1)x2+14x+49
= x2+2×7x+72
= (x+7) 2 ;
(2)(m+n)2-6(m+n)+9
= [(m+n)-3]2
=(m+n-3)2.
根据因式分解与整式乘法的关系,我们可以利用乘法公式把某些多项式因式分解,这种因式分解的方法叫做公式法.
二、自主合作,探究新知
归纳:因式分解前应先分析多项式的特点,一般先提公因式,再套用公式.分解因式必须进行到每一个多项式都不能再分解因式为止.
典型例题
例2 把下列各式因式分解:
(1)3ax2+6axy+3ay2; (2)-x2-4y2+4xy.
解:(1)3ax2+6axy+3ay2
= 3a(x2+2xy+y2)
=3a(x+y)2;
(2)-x2-4y2+4xy
= -(x2+4y2-4xy)
= -(x2-4xy+4y2)
=-[x2-2·x·2y+(2y)2]
= -(x-2y)2.
二、自主合作,探究新知
做一做:计算或化简下列各式:(1)2022+202×196+982; (2)(a2-2)2-2a2(a2-2)+a4.
探究二:平方差公式因式分解的应用
解:(1) 2022+202×196+982
=2022+2×202×98+982
=(202+98)2
=3002
=90 000.
(2) (a2-2)2-2a2(a2-2)+a4
=(a2-2)2-2a2(a2-2)+(a2)2
=(a2-2-a2)2
=(-2)2
=4.
利用完全平方公式因式分解,可以简化计算.
二、自主合作,探究新知
例3:已知a,b,c分别是△ABC三边的长,且a2+2b2+c2-2b(a+c)=0,请判断△ABC的形状,并说明理由.
∴△ABC是等边三角形.
解:由a2+2b2+c2-2b(a+c)=0,得
a2-2ab+b2+b2-2bc+c2=0,
即(a-b)2+(b-c)2=0,
∴a-b=0,b-c=0,
∴a=b=c,
典型例题
2.因式分解x2-2x+1的最终结果是( )A.x(x-2)+1 B.(x+1)(x-2)C.(x-1)2 D.(x+1)2
1.下列各式中能用完全平方公式进行因式分解的是( )
A.x2+x+1 B.x2+2x-1
C.x2-1 D.x2-6x+9
三、即学即练,应用知识
C
D
3.计算1002-2×100×99+992的值为( )A.0 B.1
C.-1 D.39601
B
5.已知9x2-mxy+16y2能运用完全平方公式因式分解,则m的值为( )A.12 B.±12
C.24 D.±24
4.把多项式8a3-8a2+2a因式分解,结果正确的是( )A.2a(4a2-4a+1) B.8a2(a-1)C.2a(2a-1)2 D.2a(2a+1)2
三、即学即练,应用知识
C
D
7.因式分解:2m2-12m+18= .
三、即学即练,应用知识
6.下列各式中,能用完全平方公式进行因式分解的是 .(填序号)①x2-2x-2;②x2+1;③x2-4x+4;④x2+4x+1.
③
2(m-3)2
8.若m=2n+1,则m2-4mn+4n2的值是________.
1
三、即学即练,应用知识
9.把下列各式因式分解:(1)-x2+2x-1; (2)9(a-b)2+42(a-b)+49;
(3)x3-2x2y+xy2; (4)x2(y2-1)+2x(y2-1)+(y2-1).
解: (1)-x2+2x-1
=-(x2-2x+1)
=-(x-1)2.
(2)9(a-b)2+42(a-b)+49
=[3(a-b)+7]2
=(3a-3b+7)2;
(3)x3-2x2y+xy2
=x(x2-2xy+y2)
=x(x-y)2;
(4)x2(y2-1)+2x(y2-1)+(y2-1)
=(x2+2x+1)(y2-1)
=(x+1)2(y+1)(y-1).
四、课堂小结
a2±2ab+b2=(a±b)2
公式法2
完全平方公式因式分解
公式法
语言叙述:两个数的平方和加上(或减去)这两个数的积的2倍,等于这两个数的和(或差)的平方.
完全平放式的特点:
1.是三项式(或可以看成三项);
2.有两个同号的数或式的平方;
3.中间是这两个数的积的±2倍.
根据因式分解与整式乘法的关系,我们可以利用乘法公式把某些多项式因式分解,这种因式分解的方法叫做公式法.
2.小华同学利用完全平方公式对下列式子进行因式分解,你认为正确的是( )A.x2+4x+4=(x+4)2B.4x2-2x+1=(2x-1)2C.9-6(m-n)+(m-n)2=(3-m-n)2D.-a2-b2+2ab=-(a-b)2
五、当堂达标检测
D
1.下列四个多项式中,能因式分解的是( )
A.a2+1 B.a2-6a+9
C.x2+5y D.x2-5y
B
五、当堂达标检测
3.把多项式4x2y-4xy2-x3分解因式的结果是( )
A.4xy(x-y)-x3 B.-x(x-2y)2
C.x(4xy-4y2-x2) D.-x(-4xy+4y2+x2)
B
4.计算:1252-50×125+252=( )
A.100 B.150
C.10 000 D.22 500
C
7.如图所示,是长与宽分别为a,b的长方形,它的周长为14,面积为10,则a3b+2a2b2+ab3的值为________.
5.因式分解(a-b)2+4ab的结果是 .
五、当堂达标检测
6.若关于x的多项式x2-8x+m2是完全平方式,则m的值为________.
±4
(a+b)2
490
五、当堂达标检测
8.把下列多项式因式分解.
(1)x2-12x+36; (2)2a2b-a3-ab2;
(3)4(2a+b)2-4(2a+b)+1; (4) y2+2y+1-x2;
(3)4(2a+b)2-4(2a+b)+1
=[2(2a+b)] - 2·2(2a+b)·1+(1)
=(4a+2b - 1)2;
解:(1)x2-12x+36
=x2-2·x·6+(6)2
=(x-6)2;
(4)y2+2y+1-x2
=(y+1) -x
=(y+1+x)(y+1-x).
(2)2a2b-a3-ab2
=-a(a2-2ab+b2)
=-a(a-b)2;
五、当堂达标检测
9.阅读材料:在因式分解中,有一类形如x2+(m+n)x+mn的多项式,其常数项是两个因数的积,而它的一次项系数恰是这两个因数的和,则我们可以把它分解:x2+(m+n)x+mn=(x+m)(x+n).例如:x2+5x+6=x2+(2+3)x+2×3=(x+2)·(x+3).运用上述方法因式分解:(1)x2+6x+8; (2)x2-x-6; (3)x2-5xy+6y2.
解: (1)x2+6x+8=(x+2)(x+4);
(2)x2-x-6=(x+2)(x-3);
(3)x2-5xy+6y2=(x-2y)(x-3y).
教材习题4.5.
六、布置作业
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
