6.10三元一次方程组及其解法-六年级数学下册同步精品课堂(沪教版)
文档属性
| 名称 | 6.10三元一次方程组及其解法-六年级数学下册同步精品课堂(沪教版) |

|
|
| 格式 | pptx | ||
| 文件大小 | 789.7KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-04-19 00:00:00 | ||
图片预览







文档简介
(共21张PPT)
6.10 三元一次方程组及其解法
沪教版六年级第二学期
第六章 —次方程(组)和一次不等式(组)
教学目标
1.会用代入消元法解一些简单的三元一次方程组;能体会“代入法”解三元一次方程组的基本思想,体现化归思想。
2.通过代入消元,使学生初步了解把“未知”转化为“已知”,和把复杂问题转化为简单问题的思想方法;培养学生的分析能力,能迅速在所给的三元一次方程组中,选择一个系数较为简单的方程进行变形。
3.逐步渗透矛盾转化的数学思想。
新课引入
问题1 这是什么方程组呢?
新知学习
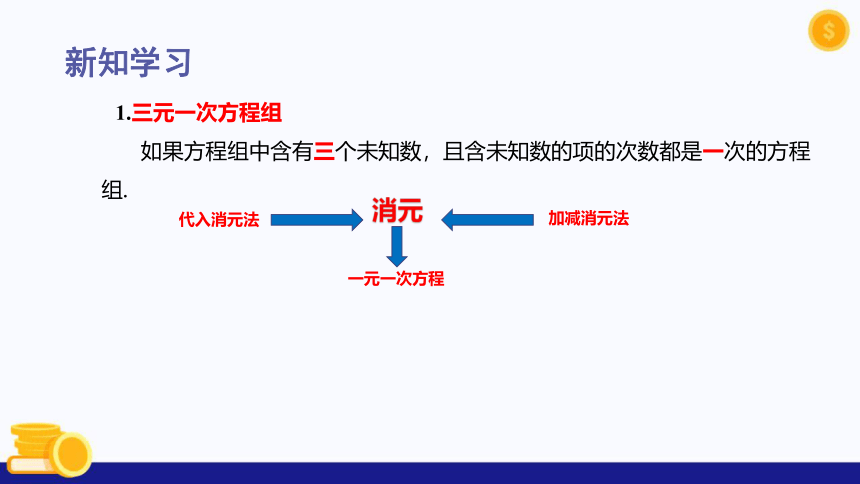
1.三元一次方程组
如果方程组中含有三个未知数,且含未知数的项的次数都是一次的方程组.
例题1 判断下列方程组中,哪些是三元一次方程组呢?
(√)
(×)
(×)
(√)
能类比二元一次方程组的解法来求解吗?
新知学习
1.三元一次方程组
如果方程组中含有三个未知数,且含未知数的项的次数都是一次的方程组.
代入消元法
加减消元法
消元
一元一次方程
新知学习
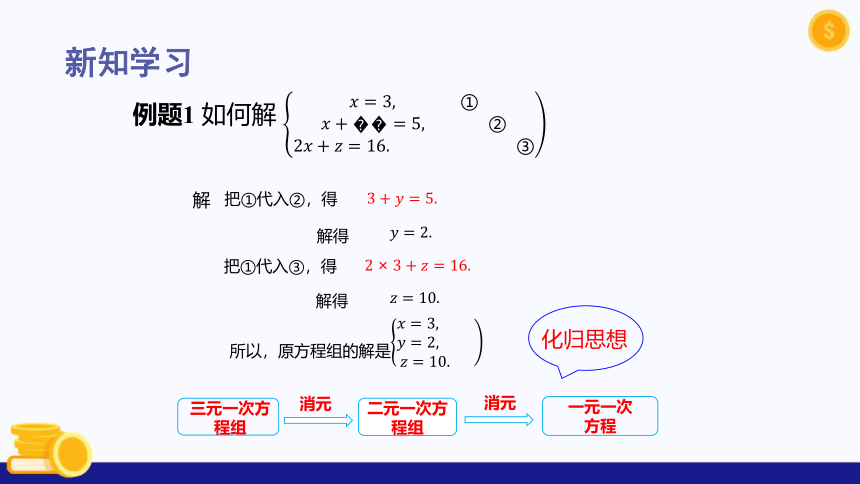
例题1 如何解
解
把①代入②,得
把①代入③,得
三元一次方程组
二元一次方
程组
一元一次方程
消元
消元
解得
解得
化归思想
例题讲解
练习1 解方程组
例题讲解
练习1 解方程组
解
由② -③,得
所以
由①-④,得
解得
把 代入①,解得
把 代入②,得
解得
例题讲解
练习1 解方程组
解
由①+②,得
即
由②+③,得
所以
由④×5-⑤,得
解得
把 代入④,解得
把 代入①,得
解得
例题讲解
练习2 解方程组
例题讲解
练习2 解方程组
解
把①代入②,得
即
把①代入③,得
即
所以
由④+⑤,得
解得
把 代入③,得
14
解得
由②+③,得
把①代入④,得
解得
例题讲解
练习2 解方程组
解
由①+③,得
即
由②+③,得
所以
由④×4-⑤,得
解得
把 代入①,解得
把 代入④,解得
新知学习
例题2 如何解
思考多种解答方法哦~
新知学习
例题2 如何解
解
由①-②,得
把 代入①,解得
方法1
由③+④,得
解得
把 代入③,解得
新知学习
例题2 如何解
方法2
由①+②+③,得
即
由④-①,得
由④-②,得
由④-③,得
方法3
由①+②-③,得
把 代入①,解得
把 代入②,解得
新知学习
例题3 如何解
由 ①+③,得
由②+③×2,得
由④×3-⑤×4,得
解得
把 代入④,解得
把 代入①,解得
由 ①+③,得
由 ②-③,得
解
所以
例题讲解
练习3 解方程组
例题讲解
练习3 解方程组
解
由①+②+③,得
解得
把 代入①,解得
把 代入②,解得
例题讲解
练习3 解方程组
例题讲解
练习3 解方程组
解
由④+⑤,得
解得
把 代入④,得
由①-④,得
方法1
由②×2-①,得
把 代入②,得
方法2
由①+②+③,得
由②-③,得
由②-④,得
由③-④,得
小结归纳
1.三元一次方程组
如果方程组中含有三个未知数,且含未知数的项的次数都是一次的方程组.
代入消元法
加减消元法
消元
一元一次方程
6.10 三元一次方程组及其解法
沪教版六年级第二学期
第六章 —次方程(组)和一次不等式(组)
教学目标
1.会用代入消元法解一些简单的三元一次方程组;能体会“代入法”解三元一次方程组的基本思想,体现化归思想。
2.通过代入消元,使学生初步了解把“未知”转化为“已知”,和把复杂问题转化为简单问题的思想方法;培养学生的分析能力,能迅速在所给的三元一次方程组中,选择一个系数较为简单的方程进行变形。
3.逐步渗透矛盾转化的数学思想。
新课引入
问题1 这是什么方程组呢?
新知学习
1.三元一次方程组
如果方程组中含有三个未知数,且含未知数的项的次数都是一次的方程组.
例题1 判断下列方程组中,哪些是三元一次方程组呢?
(√)
(×)
(×)
(√)
能类比二元一次方程组的解法来求解吗?
新知学习
1.三元一次方程组
如果方程组中含有三个未知数,且含未知数的项的次数都是一次的方程组.
代入消元法
加减消元法
消元
一元一次方程
新知学习
例题1 如何解
解
把①代入②,得
把①代入③,得
三元一次方程组
二元一次方
程组
一元一次方程
消元
消元
解得
解得
化归思想
例题讲解
练习1 解方程组
例题讲解
练习1 解方程组
解
由② -③,得
所以
由①-④,得
解得
把 代入①,解得
把 代入②,得
解得
例题讲解
练习1 解方程组
解
由①+②,得
即
由②+③,得
所以
由④×5-⑤,得
解得
把 代入④,解得
把 代入①,得
解得
例题讲解
练习2 解方程组
例题讲解
练习2 解方程组
解
把①代入②,得
即
把①代入③,得
即
所以
由④+⑤,得
解得
把 代入③,得
14
解得
由②+③,得
把①代入④,得
解得
例题讲解
练习2 解方程组
解
由①+③,得
即
由②+③,得
所以
由④×4-⑤,得
解得
把 代入①,解得
把 代入④,解得
新知学习
例题2 如何解
思考多种解答方法哦~
新知学习
例题2 如何解
解
由①-②,得
把 代入①,解得
方法1
由③+④,得
解得
把 代入③,解得
新知学习
例题2 如何解
方法2
由①+②+③,得
即
由④-①,得
由④-②,得
由④-③,得
方法3
由①+②-③,得
把 代入①,解得
把 代入②,解得
新知学习
例题3 如何解
由 ①+③,得
由②+③×2,得
由④×3-⑤×4,得
解得
把 代入④,解得
把 代入①,解得
由 ①+③,得
由 ②-③,得
解
所以
例题讲解
练习3 解方程组
例题讲解
练习3 解方程组
解
由①+②+③,得
解得
把 代入①,解得
把 代入②,解得
例题讲解
练习3 解方程组
例题讲解
练习3 解方程组
解
由④+⑤,得
解得
把 代入④,得
由①-④,得
方法1
由②×2-①,得
把 代入②,得
方法2
由①+②+③,得
由②-③,得
由②-④,得
由③-④,得
小结归纳
1.三元一次方程组
如果方程组中含有三个未知数,且含未知数的项的次数都是一次的方程组.
代入消元法
加减消元法
消元
一元一次方程
