第七章线段与角的画法(单元小结) 课件(共22张PPT)-六年级数学下册同步精品课堂(沪教版)
文档属性
| 名称 | 第七章线段与角的画法(单元小结) 课件(共22张PPT)-六年级数学下册同步精品课堂(沪教版) |

|
|
| 格式 | pptx | ||
| 文件大小 | 565.2KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-04-17 00:00:00 | ||
图片预览




文档简介
(共22张PPT)
单元小结
沪教版六年级第二学期
第七章 线段与角的画法
教学目标
1.理解余角、补角的概念.
2. 能用规范的数学符号语言描述余角、补角,并进行相关的求角问题的计算.
3. 理解有关余角、补角的两个命题.
4. 会用计算器进行角度的计算.
教学重点 余角、补角概念及有关计算.
教学难点 有关余角、补角的计算.
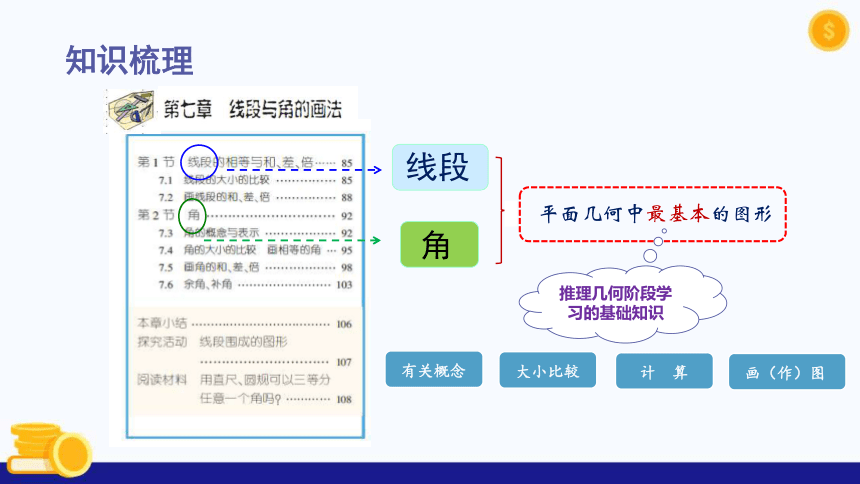
知识梳理
线段
角
平面几何中最基本的图形
推理几何阶段学习的基础知识
计 算
有关概念
大小比较
画(作)图
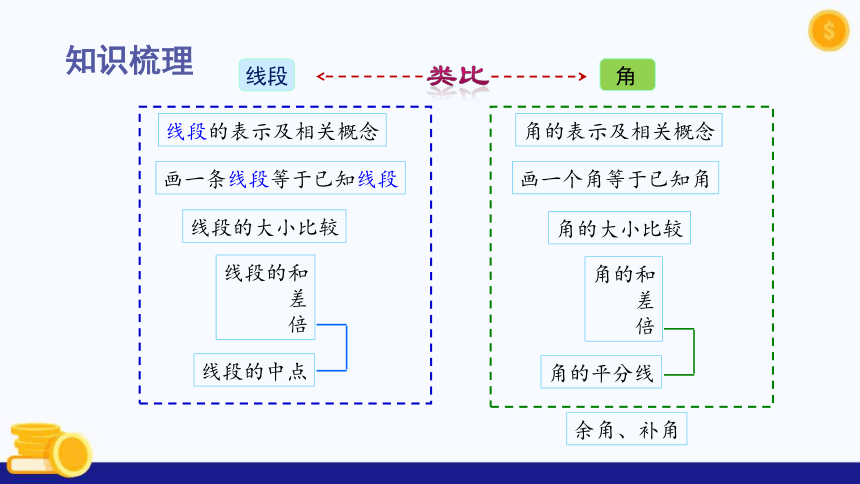
知识梳理
线段的表示及相关概念
角的表示及相关概念
画一条线段等于已知线段
画一个角等于已知角
线段的大小比较
角的大小比较
线段的和
差
倍
线段的中点
角的和
差
倍
角的平分线
线段
角
余角、补角
类比
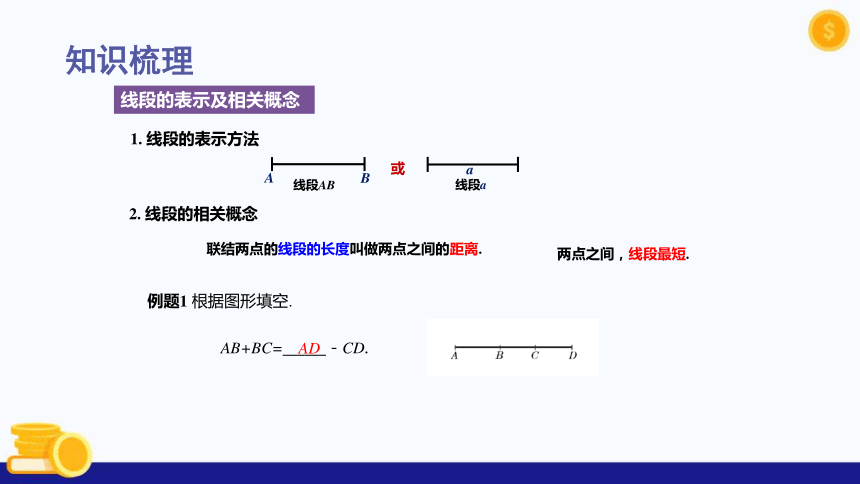
知识梳理
1. 线段的表示方法
A
联结两点的线段的长度叫做两点之间的距离.
B
a
线段AB
线段a
或
2. 线段的相关概念
两点之间,线段最短.
例题1 根据图形填空.
AB+BC=______-CD.
AD
线段的表示及相关概念
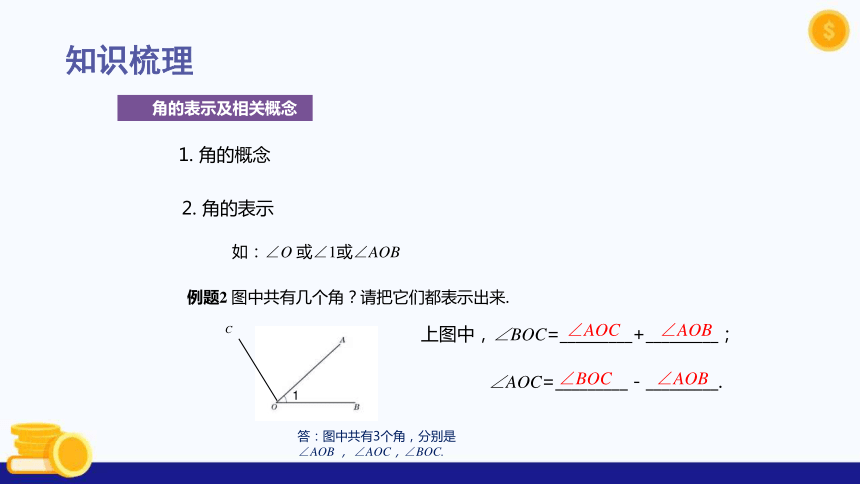
知识梳理
1. 角的概念
2. 角的表示
1
例题2 图中共有几个角?请把它们都表示出来.
∠AOC=_________-_________.
∠BOC
∠AOB
上图中,∠BOC=_________+_________;
∠AOC
∠AOB
答:图中共有3个角,分别是∠AOB , ∠AOC,∠BOC.
角的表示及相关概念
如:∠O 或∠1或∠AOB
C
例题讲解
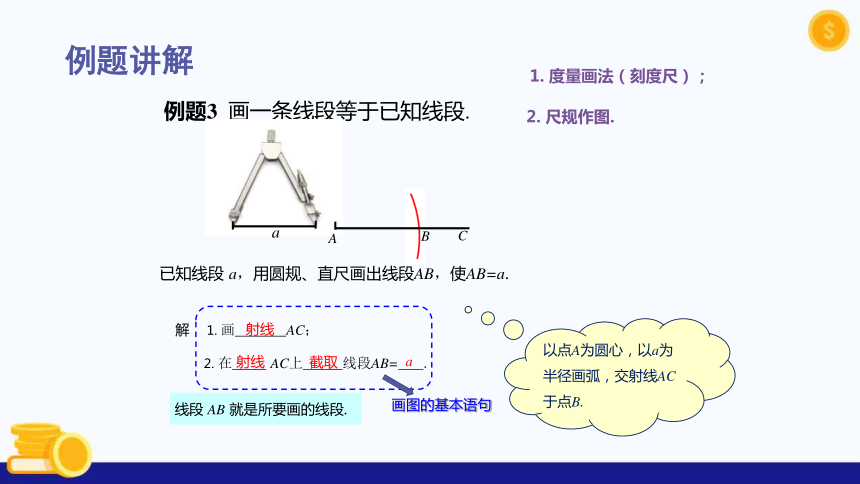
例题3 画一条线段等于已知线段.
已知线段 a,用圆规、直尺画出线段AB,使AB=a.
a
B
A
C
解 1. 画 AC;
2. 在 AC上 线段AB= .
线段 AB 就是所要画的线段.
以点A为圆心,以a为半径画弧,交射线AC于点B.
射线
射线
截取
a
画图的基本语句
1. 度量画法(刻度尺);
2. 尺规作图.
例题讲解
例题4 画一个角等于已知角.
1. 度量画法(刻度尺);
2. 尺规作图.
已知∠ β,用圆规、直尺作∠AOB,使∠AOB= ∠β.
A
β
3. 以点 为圆心、 为半径作弧,交OA
于点M .
4. 以点 为圆心、 长为半径作弧,交
前弧于点N .
5. 经过点N作 OB.
∠ AOB 就是所求作的角.
E
F
M
.
N
a
射线
顶点
半径
O
a
M
EF
射线
O
2. 以∠ β的 为圆心、取定的长a为 作弧,
分别交∠ β 的两边于点E、F;
解 1. 作 OA;
“对中、对边、读数“
例题讲解
例题5 画线段的和、差、倍.
已知线段a、b,画出一条线段, 使它等于2a-b.
.
a
b
解 (1)画射线OP;
O
P
(2)在射线OP上顺次截取OA=a,AB=a;
(3)在线段OB上截取BC=b.
A
B
C
线段 OC 就是所要画的线段.
例题讲解
例题6 画角的和、差、倍.
α
已知线段∠α、∠β ,画出∠MON, 使∠MON= 2∠α-∠β.
β
解 (1)用量角器画∠MOB= ∠α ;
(2)以点O为顶点,射线OB为一边,在∠MOB外部用量角器画∠COB= ∠α ;
O
M
B
C
(3)以点O为顶点,射线OC为一边,在∠MOC内部用量角器画∠CON= ∠ β .
N
∠ MON 就是所要画的角.
α
β
例题讲解
例题7 画线段的中点.
将一条线段分成两条相等线段的点叫做这条线段的中点.
概念
图形
A
B
E
F
C
分别以点A、B为圆心,以
大于 AB的长a为半径作弧,
两弧分别交于点E、F.
尺规作图的基本语句
表示
点 C 就是所求的线段AB的中点.
图形语言
文字语言
符号语言
例题讲解
例题8 画角的平分线.
从一个角的顶点引出一条射线,把这个角分成两个相等的角,这条射线叫做这个角的平分线.
C
O
A
B
D
E
分别以点D、E为圆心,以大于
DE的同一长度为半径作弧,两弧交于∠AOB内一点C.
OC 就是所求作的角的平分线.
或
知识梳理
余角
如果两个角的度数的和是90°,那么这两个角叫做互为余角,简称互余.其中一个角称为另一个角的余角.
∠α+∠β= 90°
∠α是∠β的余角
∠β是∠α的余角
∠α与∠β互余
同角(或等角)的余角相等.
概念
表示
命题
计算
1°=60′
1′=60″
60进位制
角的度量单位度、分、秒的关系
知识梳理
概念
表示
命题
计算
补角
如果两个角的度数的和是180°,那么这两个角叫做互为补角,简称互补.其中一个角称为另一个角的补角.
∠α+∠β= 180°
∠α是∠β的补角
∠β是∠α的补角
∠α与∠β互补
同角(或等角)的补角相等.
如果∠α=47°28′,那么
同一个锐角的补角比它的余角大90°.
∠α的余角∠β = ,
∠α的补角∠γ= ,
∠γ - ∠α= .
90°-47°28′
=89°60′-47°28′
=42°32′
180°-47°28′
=179°60′-47°28′
=132°32′
42°32′
132°32′
90°
(1)锐角既有余角又有补角. ( )
(2)锐角不小于它的补角. ( )
(3)互补的两个角一个是锐角,一个是钝角. ( )
(4)一个锐角的余角比它的补角小90°. ( )
(5)只有补角而没有余角的角是钝角. ( )
(6)同角或等角的余角一定相等. ( )
(8)因为∠1+∠2+∠3=180 ,所以∠1、∠2与∠3互为补角. ( )
√
╳
╳
╳
√
╳
√
如果两个角的度数的和是180°,那么这两个角叫做互为补角,简称互补.
锐角一定小于它的补角.
如:一个直角的补角仍是直角.
若α是锐角,则(180°- α )-(90°- α )=90°.
如:直角也只有补角没有余角.
(7)如果∠1=34 58′08″,那么∠1的余角是55 1′52″. ( )
90°-34 58′08″
89 59′60″
-34 58′08″
52″
1′
55
√
概念辨析
课堂练习
练习1如图,已知点B是线段AC上的一点,如果点M是线段AB的中点,点N是线段AC的中点,那么BC= MN.
点M是线段AB的中点
AB=2AM=2MB=2x
分析
点N是线段AC的中点
AC=2AN=2NC=2y
设AM=x,
BC=2y-2x
又MN=AN-AM
AN=y,
又BC=AC-AB
即BC=2(y-x)
即MN=y-x
BC= 2 MN.
x
A
C
B
N
.
.
.
M
x
y
y
课堂练习
练习2如图,点A、O、B在同一条直线上,OD、OE分别是∠AOC、 ∠BOC 的平分线, 那么∠DOE= .
C
O
D
E
B
A
分析
∠AOC+∠BOC=180°
∠DOC= ∠AOC
∠COE= ∠BOC
∠DOE=
(∠AOC+∠BOC)
∠DOE=90°.
课堂练习
练习3 如图,已知直线AB和CD相交于点O,∠COE是直角,OF 平分∠AOE, ∠COF=34°,求∠BOD的度数.
O
A
B
F
34°
所以∠COE = ,
因为∠COF=34°,
因为OF 平分∠AOE,
所以∠AOF= ,
E
所以∠EOF = .
56°
所以∠AOC =∠AOF - = .
因为直线AB和CD相交于点O,
所以∠AOC +∠BOC=∠BOD+∠BOC=180°.
所以∠BOD= = .
D
C
90°
90°- ∠COF
90 °- 34°= 56°
∠EOF=56°
∠COF
22°
22°
∠AOC
同角的补角相等.
22°
例题讲解
例题7 如图,O是直线AB 上的一点,AOC=90°,∠DOE=90°, 图中共有几对互余的角?请写出所有互余的角.
例题讲解
例题7 如图,O是直线AB 上的一点,AOC=90°,∠DOE=90°, 图中共有几对互余的角?请写出所有互余的角.
C
O
D
E
B
A
即∠AOB=180°
∠AOC=90°
∠AOC=90°
1
2
3
4
即∠1+∠2=90°
∠BOC=90°即∠3+∠4=90°
∠1与∠2互余
∠1=∠3
答:图中共有4对互余的角,分别是∠1与∠2、 ∠2与∠3、 ∠1与∠4、 ∠3与∠4.
同角的余角相等.
∠DOE=90°
即∠3+∠2=90°
∠3与∠2互余
O是直线AB 上的一点,
∠3与∠4互余
∠1与∠4互余
分析
课堂练习
练习4 已知∠AOB=60°,∠BOC与∠AOB互余,OP平分∠AOC.
(1)画出所有符合条件的图形.
(2)计算∠BOP的度数.
解 (1)
∠AOC=
30°
C
P
O
60°
A
B
①当OC在∠AOB的外部时,
②当OC在∠AOB的内部时,
∠AOB
+∠BOC
= .
90°
又OP平分∠AOC,
所以∠COP=
∠AOC
即∠BOP=
∠COP-∠BOC
= .
15°
= .
45°
30°
C
P
O
60°
A
B
(2)
∠AOC=
∠AOB
-∠BOC
= .
30°
又OP平分∠AOC,
所以∠COP=
∠AOC
即∠BOP=
∠COP+∠BOC
= .
45°
= .
15°
归纳小结
线段的表示及相关概念
角的表示及相关概念
画一条线段等于已知线段
画一个角等于已知角
线段的大小比较
角的大小比较
线段的和
差
倍
线段的中点
角的和
差
倍
角的平分线
线段
角
余角、补角
类比
单元小结
沪教版六年级第二学期
第七章 线段与角的画法
教学目标
1.理解余角、补角的概念.
2. 能用规范的数学符号语言描述余角、补角,并进行相关的求角问题的计算.
3. 理解有关余角、补角的两个命题.
4. 会用计算器进行角度的计算.
教学重点 余角、补角概念及有关计算.
教学难点 有关余角、补角的计算.
知识梳理
线段
角
平面几何中最基本的图形
推理几何阶段学习的基础知识
计 算
有关概念
大小比较
画(作)图
知识梳理
线段的表示及相关概念
角的表示及相关概念
画一条线段等于已知线段
画一个角等于已知角
线段的大小比较
角的大小比较
线段的和
差
倍
线段的中点
角的和
差
倍
角的平分线
线段
角
余角、补角
类比
知识梳理
1. 线段的表示方法
A
联结两点的线段的长度叫做两点之间的距离.
B
a
线段AB
线段a
或
2. 线段的相关概念
两点之间,线段最短.
例题1 根据图形填空.
AB+BC=______-CD.
AD
线段的表示及相关概念
知识梳理
1. 角的概念
2. 角的表示
1
例题2 图中共有几个角?请把它们都表示出来.
∠AOC=_________-_________.
∠BOC
∠AOB
上图中,∠BOC=_________+_________;
∠AOC
∠AOB
答:图中共有3个角,分别是∠AOB , ∠AOC,∠BOC.
角的表示及相关概念
如:∠O 或∠1或∠AOB
C
例题讲解
例题3 画一条线段等于已知线段.
已知线段 a,用圆规、直尺画出线段AB,使AB=a.
a
B
A
C
解 1. 画 AC;
2. 在 AC上 线段AB= .
线段 AB 就是所要画的线段.
以点A为圆心,以a为半径画弧,交射线AC于点B.
射线
射线
截取
a
画图的基本语句
1. 度量画法(刻度尺);
2. 尺规作图.
例题讲解
例题4 画一个角等于已知角.
1. 度量画法(刻度尺);
2. 尺规作图.
已知∠ β,用圆规、直尺作∠AOB,使∠AOB= ∠β.
A
β
3. 以点 为圆心、 为半径作弧,交OA
于点M .
4. 以点 为圆心、 长为半径作弧,交
前弧于点N .
5. 经过点N作 OB.
∠ AOB 就是所求作的角.
E
F
M
.
N
a
射线
顶点
半径
O
a
M
EF
射线
O
2. 以∠ β的 为圆心、取定的长a为 作弧,
分别交∠ β 的两边于点E、F;
解 1. 作 OA;
“对中、对边、读数“
例题讲解
例题5 画线段的和、差、倍.
已知线段a、b,画出一条线段, 使它等于2a-b.
.
a
b
解 (1)画射线OP;
O
P
(2)在射线OP上顺次截取OA=a,AB=a;
(3)在线段OB上截取BC=b.
A
B
C
线段 OC 就是所要画的线段.
例题讲解
例题6 画角的和、差、倍.
α
已知线段∠α、∠β ,画出∠MON, 使∠MON= 2∠α-∠β.
β
解 (1)用量角器画∠MOB= ∠α ;
(2)以点O为顶点,射线OB为一边,在∠MOB外部用量角器画∠COB= ∠α ;
O
M
B
C
(3)以点O为顶点,射线OC为一边,在∠MOC内部用量角器画∠CON= ∠ β .
N
∠ MON 就是所要画的角.
α
β
例题讲解
例题7 画线段的中点.
将一条线段分成两条相等线段的点叫做这条线段的中点.
概念
图形
A
B
E
F
C
分别以点A、B为圆心,以
大于 AB的长a为半径作弧,
两弧分别交于点E、F.
尺规作图的基本语句
表示
点 C 就是所求的线段AB的中点.
图形语言
文字语言
符号语言
例题讲解
例题8 画角的平分线.
从一个角的顶点引出一条射线,把这个角分成两个相等的角,这条射线叫做这个角的平分线.
C
O
A
B
D
E
分别以点D、E为圆心,以大于
DE的同一长度为半径作弧,两弧交于∠AOB内一点C.
OC 就是所求作的角的平分线.
或
知识梳理
余角
如果两个角的度数的和是90°,那么这两个角叫做互为余角,简称互余.其中一个角称为另一个角的余角.
∠α+∠β= 90°
∠α是∠β的余角
∠β是∠α的余角
∠α与∠β互余
同角(或等角)的余角相等.
概念
表示
命题
计算
1°=60′
1′=60″
60进位制
角的度量单位度、分、秒的关系
知识梳理
概念
表示
命题
计算
补角
如果两个角的度数的和是180°,那么这两个角叫做互为补角,简称互补.其中一个角称为另一个角的补角.
∠α+∠β= 180°
∠α是∠β的补角
∠β是∠α的补角
∠α与∠β互补
同角(或等角)的补角相等.
如果∠α=47°28′,那么
同一个锐角的补角比它的余角大90°.
∠α的余角∠β = ,
∠α的补角∠γ= ,
∠γ - ∠α= .
90°-47°28′
=89°60′-47°28′
=42°32′
180°-47°28′
=179°60′-47°28′
=132°32′
42°32′
132°32′
90°
(1)锐角既有余角又有补角. ( )
(2)锐角不小于它的补角. ( )
(3)互补的两个角一个是锐角,一个是钝角. ( )
(4)一个锐角的余角比它的补角小90°. ( )
(5)只有补角而没有余角的角是钝角. ( )
(6)同角或等角的余角一定相等. ( )
(8)因为∠1+∠2+∠3=180 ,所以∠1、∠2与∠3互为补角. ( )
√
╳
╳
╳
√
╳
√
如果两个角的度数的和是180°,那么这两个角叫做互为补角,简称互补.
锐角一定小于它的补角.
如:一个直角的补角仍是直角.
若α是锐角,则(180°- α )-(90°- α )=90°.
如:直角也只有补角没有余角.
(7)如果∠1=34 58′08″,那么∠1的余角是55 1′52″. ( )
90°-34 58′08″
89 59′60″
-34 58′08″
52″
1′
55
√
概念辨析
课堂练习
练习1如图,已知点B是线段AC上的一点,如果点M是线段AB的中点,点N是线段AC的中点,那么BC= MN.
点M是线段AB的中点
AB=2AM=2MB=2x
分析
点N是线段AC的中点
AC=2AN=2NC=2y
设AM=x,
BC=2y-2x
又MN=AN-AM
AN=y,
又BC=AC-AB
即BC=2(y-x)
即MN=y-x
BC= 2 MN.
x
A
C
B
N
.
.
.
M
x
y
y
课堂练习
练习2如图,点A、O、B在同一条直线上,OD、OE分别是∠AOC、 ∠BOC 的平分线, 那么∠DOE= .
C
O
D
E
B
A
分析
∠AOC+∠BOC=180°
∠DOC= ∠AOC
∠COE= ∠BOC
∠DOE=
(∠AOC+∠BOC)
∠DOE=90°.
课堂练习
练习3 如图,已知直线AB和CD相交于点O,∠COE是直角,OF 平分∠AOE, ∠COF=34°,求∠BOD的度数.
O
A
B
F
34°
所以∠COE = ,
因为∠COF=34°,
因为OF 平分∠AOE,
所以∠AOF= ,
E
所以∠EOF = .
56°
所以∠AOC =∠AOF - = .
因为直线AB和CD相交于点O,
所以∠AOC +∠BOC=∠BOD+∠BOC=180°.
所以∠BOD= = .
D
C
90°
90°- ∠COF
90 °- 34°= 56°
∠EOF=56°
∠COF
22°
22°
∠AOC
同角的补角相等.
22°
例题讲解
例题7 如图,O是直线AB 上的一点,AOC=90°,∠DOE=90°, 图中共有几对互余的角?请写出所有互余的角.
例题讲解
例题7 如图,O是直线AB 上的一点,AOC=90°,∠DOE=90°, 图中共有几对互余的角?请写出所有互余的角.
C
O
D
E
B
A
即∠AOB=180°
∠AOC=90°
∠AOC=90°
1
2
3
4
即∠1+∠2=90°
∠BOC=90°即∠3+∠4=90°
∠1与∠2互余
∠1=∠3
答:图中共有4对互余的角,分别是∠1与∠2、 ∠2与∠3、 ∠1与∠4、 ∠3与∠4.
同角的余角相等.
∠DOE=90°
即∠3+∠2=90°
∠3与∠2互余
O是直线AB 上的一点,
∠3与∠4互余
∠1与∠4互余
分析
课堂练习
练习4 已知∠AOB=60°,∠BOC与∠AOB互余,OP平分∠AOC.
(1)画出所有符合条件的图形.
(2)计算∠BOP的度数.
解 (1)
∠AOC=
30°
C
P
O
60°
A
B
①当OC在∠AOB的外部时,
②当OC在∠AOB的内部时,
∠AOB
+∠BOC
= .
90°
又OP平分∠AOC,
所以∠COP=
∠AOC
即∠BOP=
∠COP-∠BOC
= .
15°
= .
45°
30°
C
P
O
60°
A
B
(2)
∠AOC=
∠AOB
-∠BOC
= .
30°
又OP平分∠AOC,
所以∠COP=
∠AOC
即∠BOP=
∠COP+∠BOC
= .
45°
= .
15°
归纳小结
线段的表示及相关概念
角的表示及相关概念
画一条线段等于已知线段
画一个角等于已知角
线段的大小比较
角的大小比较
线段的和
差
倍
线段的中点
角的和
差
倍
角的平分线
线段
角
余角、补角
类比
