专题03四边形(考点串讲)-八年级数学下学期期中考点大串讲(沪教版)
文档属性
| 名称 | 专题03四边形(考点串讲)-八年级数学下学期期中考点大串讲(沪教版) |

|
|
| 格式 | pptx | ||
| 文件大小 | 3.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-04-19 00:00:00 | ||
图片预览











文档简介
(共86张PPT)
八年级沪教版数学下册期中考点大串讲
串讲03 四边形
技巧总结
01
02
04
05
03
目
录
易错易混
典例剖析
考点透视
考场练兵
首尾顺次
n边形
相邻两边
延长线
n
n
n
n
D
考点透视
不相邻
7
C
相等
相等
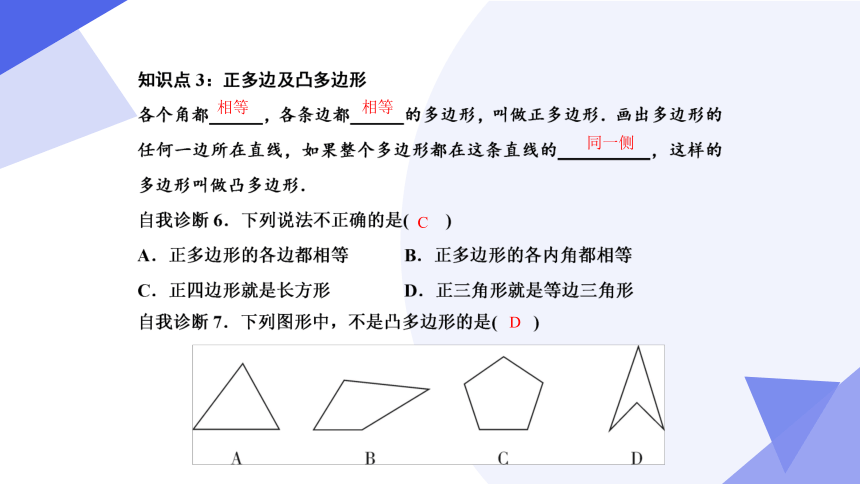
同一侧
C
D
(n-2)×180°
C
C
360°
B
相等
相等
互补
十
C
平行四边形
ABCD
平行四边形
两组对边分别平行的四边形叫平行四边形
相等
相等
5cm
125°
55°
125°
互相平分
21
全等
相等
2
2
8
3<x<13
相等
相等
118°
互相平分
C
平行且相等
4
中点
平行
一半
3
B
直角
平行且相等
都是直角
互相平分且相等
2
等于斜边的一半
5
相等
B
三
C
邻边
两条对角线所在的直线
相等
互相垂直平分
平分
16
一半
24
有一组邻边相等
四条边相等
对角线互相垂直
四条边相等的四边形是菱形
直角
相等
互相垂直平分且相等
22.5°
相等
直角
矩形
菱形
D
一组对边平行而另一组对边不平行的四边形叫做梯形(trapezium).在梯形中,平行的两边叫做梯形的底(通常把较短的底叫做上底,较长的底叫做下底);不平行的两边叫做梯形的腰;两底之间的距离叫做梯形的高(如图 22 -46(1)).
如图 22 - 46(2)(3),有一个角是直角的梯形叫做直角梯形(right-angled trapezium);两腰相等的梯形叫做等腰梯形(isoscelestrapezium),它们都是特殊的梯形.
知识点27:梯形
自我诊断35.在直角梯形ABCD中,AD//BC, ∠ A=90°,
AD=10cm,DC=13cm,BC=15cm,求AB的长。
作高,将梯形问题转化成直角三角形和矩形.
解:作DE⊥BC于点E ,则∠DEB=90°
∵ AD//BC,
∴ ∠A+ ∠ B=180 °
∵ ∠A=90 °
∴ ∠B=90 °
∵ ∠A=90 °,∠B=90 °,∠DEB=90°
∴四边形ABED是矩形
∴AD= BE,AB=DE
∵AD=10cm,BC=15cm
∴EC=BC-BE=BC-AD=5cm
在Rt△DEC中,
∵ ∠DEC=90°
∴
∴AB=12cm
自我诊断36.如图,在梯形ABCD中,AB//CD,
∠D=2 ∠B,AD=10,AB=15,求CD的长。
平移一腰,将梯形问题转化成三角形和
平行四边形.
解:作CE //DA交AB于点E
∵ AB//DC, CE //DA
∴四边形AECD是平行四边形
∴CE=DA, DC=AE, ∠D= ∠ 1
∵AD=10 ,∠D= 2∠ B
∴CE=10, ∠1= 2∠ B
∵ ∠1= ∠ B+ ∠ 2
∴∠2= ∠ B
∴EB= EC=10
∵AB=15
∴AE=AB-EB=5
∴CD=5
E
1
2
知识点28:等腰梯形的三种判定方法:
①两腰相等的梯形是等腰梯形。
②同一底上的两个底角相等的梯形是等腰梯形。
③对角线相等的梯形是等腰梯形。
自我诊断37.已知:矩形ABCD中,点E、F在边AD上,AE=FD。
求证:四边形EBCF等腰梯形。
证明:∵ 四边形ABCD是矩形
∴ AB=DC,AD∥BC,
∠A=∠D=900
∵ AE=DF
∴ △ABE≌△DCF(SAS)
∴ EB=FC
又 ∵ EF∥BC,且EF≠BC,
∴四边形 EFCB是梯形
∴ 四边形EBCF是等腰梯形(两腰相等的梯形是等腰梯形)
A E F D
B C
梯形的中位线平行于两底,并且等于两底和的一半
知识点29:梯形中位线定理:
∵AD ∥BC
AM=MB,DN=NC
∴ MN ∥ BC
MN=(BC+AD)
(梯形的中位线平行于两底,并且等于两底和的一半)
自我诊断38.一个梯形的上底长4 cm,下底长6 cm,则其中位线长为 cm;
自我诊断39.一个梯形的上底长10 cm,中位线长16 cm,则其下底长为 cm;
5
22
向量:既有大小、又有方向的量.
几何表示:
有向线段
A
B
符号语言: ,
模: ,
位置向量
自由向量
相等向量
相反向量
平行向量
向量的模型——位移
从始点A出发到终点B的过程中的位移为 .
位移由运动过程中的始点和终点确定,而与运动的路径无关.
知识点30:平面向量
一、向量加法的运算(作图)法则:
二、向量减法的运算(作图)法则:
1、三角形法则,(起点和终点重合)
2、多边形形法则(首尾依次相连接)
1、三角形法则(共起点,尾相连)
3、平行四边形法则(共起点,做平行四边形)
2、平行四边形法则(共起点,做平行四边形)
以共起点为起点的对角线向量,就是a,b的和向量;
与被减向量共终点的对角线向量,就是a,b的差向量。
知识点31:平面向量的加减
自我诊断40.不画图怎样直接计算:
______________
______________
______________
“共”“起”点
“减”到“被”
向量减法的要领是什么?
A
C
典例剖析
不唯一,如DE=EC
32cm或34cm
C
AB=BC或AC⊥BD
A
B
易错易混
B
C
(3,2)或(-3,2)或(5,-2)
技巧1:特殊平行四边形的证明与计算
技巧总结
C
A
B
技巧2:四边形中的图形变换
C
B
5
6
40°
B
技巧3:解决梯形问题的基本思路和方法:
通过添加适当的辅助线,把梯形问题转化为平行四边形和三角形的问题来解决。
常画的辅助线有以下几种:
B
A
D
C
E
作一腰平行线
B
A
D
C
E
F
作高线
E
B
A
D
C
延长两腰
B
C
D
A
O
E
作对角线的平行线
1.一个多边形的内角和是540°,这个多边形是( ____ )
A.五边形
B.六边形
C.七边形
D.八边形
【解析】解:设多边形的边数是n,则
(n-2) 180°=540°,
解得n=5,
∴这个多边形是五边形,
故选:A.
A
考场练兵
2.下列等式中不正确的是( ____ )
A.
B.-(- )=
C.( + )+ = +( + )
D. +(- )= -
【解析】解:A、 ,符合题意;
B、-(- )= ,不符合题意;
C、( + )+ = +( + ),不符合题意;
A
D、 +(- )= - ,不符合题意.
故选:A.
3.如图,已知四边形ABCD是平行四边形,那么添加下列条件能判定四边形ABCD是正方形的是( ____ )
A.AB=AD且AC⊥BD
B.AC⊥BD且AC和BD互相平分
C.∠BAD=∠ABC且AC=BD
D.AC=BD且AB=AD
【解析】解:A、AB=AD且AC⊥BD,是菱形,不符合题意;
B、对角线互直垂直且互相平分,是菱形,不符合题意;
C、∠BAD=∠ABC且AC=BD不能判断四边形ABCD是正方形,不符合题意;
D
D、AC=BD且AB=AD四边相等,是正方形,符合题意;
故选:D.
4.已知梯形的四条边长分别是4、5、7、8,则中位线长可以为( ____ )
A.4.5 B.5.5 C.6 D.6.5
【解析】解:如图,过D作DE∥AB,∴BE=AD,AB=DE,
∵梯形的四条边长分别是4、5、7、8,
当梯形的两底长分别为4和8,腰分别为5和7,
即DE=5,BE=4,
C
∴CE=4,
∵4+5>7,∴DE,CE,CD能构成三角形,
∴中位线长= (4+8)=6,
当梯形的两底长分别为5和8,腰分别为4和7,DE,CE,CD不能构成三角形,其他情况也是一样,
综上所述,中位线长可以为6,故选:C.
5.如果O是正方形ABCD对角线AC、BD的交点,那么向量 、 、 、 是( ____ )
A.相等向量 B.相反向量
C.平行向量 D.模相等的向量.
【解析】解:∵O是正方形ABCD对角线AC、BD的交点,
∴OA=OC=OB=OD,
∴| |=| |=| |=| |,
D
∵ 、 、 、 的方向不同,
∴ 、 、 、 是模相等的量,
故选:D.
6.四边形不具有稳定性.四条边长都确定的四边形,当内角的大小发生变化时,其形状也随之改变.如图,改变正方形ABCD的内角,使正方形ABCD变为菱形ABC′D′,如果∠DAD′=30°,那么菱形ABC′D′与正方形ABCD的面积之比是( ____ )
A. B. C. D.1
A
【解析】解:过D'作D'M⊥AB于M,如图所示:则∠D'MA=90°,
∵四边形ABCD是正方形,∴正方形ABCD的面积=AB2,AB=AD,∠BAD=90°,
∵∠DAD′=30°,∴∠D'AM=90°-30°=60°,∴∠AD'M=30°,
∴AM= AD',D'M= AM= AD',
∵四边形ABC′D′是菱形,∴AB=AD'=AD,菱形ABCD的面积=AB×D'M= AB2,
∴菱形ABC′D′与正方形ABCD的面积之比= = ,故选:A.
7.如图,菱形ABCD的对角线的长分别为12和15,P是对角线AC上任一点(点P不与点A、C重合)且PE∥BC交AB于E,PF∥CD交AD于F,那么阴影部分的面积是 ____ .
【解析】解:设AP与EF相交于O点.∵四边形ABCD为菱形,
45
∴BC∥AD,AB∥CD.
∵PE∥BC,PF∥CD,
∴PE∥AF,PF∥AE.
∴四边形AEFP是平行四边形.
∴阴影部分的面积等于△ABC的面积.
∵△ABC的面积等于菱形ABCD的面积的一半,
∴菱形ABCD的面积= AC BD=90,
∴图中阴影部分的面积为90÷2=45.
故答案为:45.
8.已知菱形的周长为40,一条对角线长为12,则这个菱形的面积是 ____ .
【解析】解:因为周长是40,所以边长是10.
如图所示:AB=10,AC=12.
根据菱形的性质,AC⊥BD,AO=6,
∴BO=8,BD=16.
∴面积S= AC×BD=12×16× =96.
故答案为96.
96
9.如图,在等腰梯形ABCD中,AB∥CD,对角线AC⊥BC,∠B=60°,BC=6cm,则梯形ABCD的周长为 ____ .
【解析】解:∵在等腰梯形ABCD中,AB∥CD,
∴AD=BC=6,
∵AC⊥BC,∠B=60°,
∴∠BAC=30°,∠DAB=∠B=60°,
∴AB=2BC=12,∠DAC=30°,
∵AB∥CD,
∴∠DCA=∠BAC=30°,
30
∴∠DAC=∠DCA,
∴AD=CD=6,
∴等腰梯形的周长为:AB+BC+CD+AD=12+6+6+6=30.
故答案为:30.
10.如图,已知在△ABC中,点D是边AC的中点,设 ,用向量 、 表示向量 = .
【解析】解:∵点D是边AC的中点,
∴ ,
又∵ ,
∴ =- ,
故答案为:- .
11.如图,在 ABCD中,AE⊥BC、AF⊥CD,垂足分别为E、F,若∠B=50°,则∠FAE的度数是 _____ .
【解析】解:∵四边形ABCD是平行四边形,
∴AB∥CD,
∵∠B=50°,
∴∠C=180°-∠B=130°,
∵AE⊥BC、AF⊥CD,
∴∠AEC=∠AFC=90°,
∴∠FAE=360°-∠AEC-∠AFC-∠C=50°,
故答案为:50°.
50°
12.一个多边形的内角和是2880°,则这个多边形是 ____ 边形.
【解析】解:设这个多边形是n边形,根据题意,得
(n-2)×180°=2880°,
∴n=18.
故答案为:18.
18
13.我们把对角线与一边垂直的平行四边形叫做“优美平行四边形”.如果一个“优美平行四边形”的一组邻边长为 和4,那么它的最大的内角为 _____ 度.
【解析】解:如图所示:
在平行四边形ABCD中,AB⊥AC,AB=2 ,BC=4时,∠BAD最大;
由勾股定理得:AC= =2 ,
∴AC=AB,
∴∠B=45°,
135
∴∠BAD=180°-∠B=135°.
故答案为:135.
14.如图,已知平行四边形ABCD的对角线AC、BD相交于点O,OE⊥AC交AD边于点E,若△EDC的周长为15厘米,则平行四边形ABCD的周长为 ____ 厘米.
【解析】解:∵四边形ABCD是平行四边形,
∴O点为AC中点.
∵OE⊥AC,
∴AE=CE.
∴△EDC的周长=CD+CE+DE=CD+AE+DE=CD+AD=15.
∴平行四边形ABCD周长为2×15=30.
30
故答案为:30.
15.如图,梯形ABCD中,AD∥BC,∠BAC=90°,AB=AC,对角线AC与BD相交于点O,且BD=BC,那么∠AOB= ____ 度.
【解析】解:如图,作AF⊥BC于F,DE⊥BC于E,
在Rt△ABC中,
∵AB=AC,∠BAC=90°,
∴∠ABC=∠ACB=45°,
∴BC= AB,AF= AB,
∴AF= BC.
75
又∵DE=AF,
∴DE= BC= BD,
∴ = ,
∴sin∠1= ,
∴∠1=30°,
∴∠BOC=180°-30°-45°=105°,
∴∠AOB=180°-∠BOC=180°-105°=75°,
故答案为:75.
16.如图,在梯形ABCD中,AB∥CD,点E、F分别是AD、BC的中点,如果AB=2,EF=3,那么CD= ____ .
【解析】解:在梯形ABCD中,AB∥CD,点E、F分别是AD、BC的中点,
∴EF是梯形ABCD的中位线,
∴EF= (AB+CD),
∴CD=2EF-AB=6-2=4.
故答案为:4.
4
17.如图,在Rt△ABC中,∠BAC=90°,AD是△ABC的中线,点E,F分别是AD,AC的中点,连接EF,若EF=3,则AD的长为 ____ .
【解析】解:∵点E,F分别是AD,AC的中点,
∴EF是△ACD的中位线,
∴ ,
∴CD=6,
∵∠BAC=90°,AD是△ABC的中线,
∴AD=CD=6.
故答案为:6.
6
18.对于任意三角形,如果存在一个菱形,使得这个菱形的一条边与三角形的一条边重合,且三角形的这条边所对的顶点在菱形的这条边的对边上,那么称这个菱形为该三角形的“最优覆盖菱形”.
问题:如图,在△ABC中,AB=AC,BC=4,且△ABC的面积为m.如果△ABC存在“最优覆盖菱形”为菱形BCMN,那么m的取值范围 .
【解析】解:∵△ABC的面积为m,
∴△ABC的BC边上的为高 ,
如图:当高取最小值时,△ABC为等边三角形,
点A与M或N重合,
____
如图:过A作AD⊥BC,垂足为D
∵等边三角形ABC,BC=4,
∴∠ABC=60°,BC=4,∠BAD=30°.
∴BD=2,
∴AD= BD=2 ,
∴ =2 ,即m=4 .
如图:
___
当高取最大值时,菱形为正方形,
∴点A在MN的中点,∴ =4,
∴m=8,∴4 ≤m≤8,
故答案为:4 ≤m≤8.
19.如图,已知在平行四边形ABCD中,∠BAD的角平分线AE交CD于点F,交BC的延长线于点E.
(1)求证:BE=CD;
(2)若BF恰好平分∠ABE,连接AC、DE,求证:四边形ACED是平行四边形.
【解析】证明:(1)∵四边形ABCD是平行四边形,
∴AD∥BC,AB=CD,∴∠DAE=∠AEB,
∵AE平分∠BAD,∴∠BAE=∠DAE,
∴∠BAE=∠AEB,
∴BE=AB,
∴BE=CD;
(2)∵BE=AB,BF平分∠ABE,
∴AF=EF,
在△ADF和△ECF中,
,
∴△ADF≌△ECF(ASA),
∴DF=CF,
又∵AF=EF,
∴四边形ACED是平行四边形.
20.已知:如图矩形ABCD中,AC和BD相交于点O,设 , .
(1)填空: = ;(用a、b的式子表示)
(2)在图中求作 .
(不要求写出作法,只需写出结论即可.)
【解析】解:(1)∵ , , ,
∴ = ,
故答案为: ;
(2)如图所示, 即为所求;
__
21.如图,已知在△ABC中,AB=AC,点O是△ABC内任意一点,点D、G、E、F分别是AB,AC,OB,OC的中点.
(1)求证:四边形DEFG是平行四边形;
(2)若∠A=2∠BDE,求证:四边形DEFG是矩形.
【解析】证明:(1)∵点D、G、E、F分别是AB,AC,OB,OC的中点,
∴DG是△ABC的中位线,
∴DG∥BC,DG= BC,
同理:EF∥BC,EF= BC,
∴DG∥EF,DG=EF,
∴四边形DEFG是平行四边形;
(2)∵点D、E、F、G分别是AB、AC、OB、OC的中点,
∴DG是△ABC的中位线,EF是△OBC的中位线,
∴DG∥BC,DG= BC,EF∥BC,EF= BC,
∴∠ADG=∠ABC,∠AGD=∠ACB,DG∥EF,DG=EF,
∴四边形DEGF是平行四边形,
∵AB=AC,∴∠ABC=∠ACB,
∴∠ADG=∠AGD,
∵∠ADG+∠AGD+∠A=180°,即2∠ADG+∠A=180°,
∴∠ADG+ ∠A=90°,
∵∠A=2∠BDE,∴∠BDE= ∠A,
∴∠ADG+∠BDE=90°,
∴∠EDG=180°-∠ADG-∠BDE=180°-90°=90°,
∴四边形DEFG是矩形.
22.如图,已知 ABCD,过点D作DE⊥BC交CB延长线于点E,过点C作CF∥DE交AD的延长线于点F.
(1)求证:四边形DECF是矩形;
(2)设DE边与AB相交于点G,连结CG、BD,若CG=BD,求证:∠FDC=∠BGE.
【解析】证明:(1)∵四边形ABCD是平行四边形,
∴AD∥BC,
∵CF∥DE,
∴四边形DECF是平行四边形,
∵DE⊥BC,
∴∠DEC=90°,
∴四边形DECF是矩形;
(2)如图,
____
∵BG∥CD,CG=BD,
∴四边形DGBC为等腰梯形,
∴DG=CB,
∵AD=BC,
∴AD=DG,
∵∠ADG=∠FDG=90°,
∴∠DAG=∠DGA=45°,
∴∠BGE=∠DGA=45°,
∵AB∥DC,
∴∠CDG=∠DGA=45°,
∴∠FDC=∠FDE-∠CDG=90°-45°=45°,
∴∠FDC=∠BGE.
八年级沪教版数学下册期中考点大串讲
串讲03 四边形
技巧总结
01
02
04
05
03
目
录
易错易混
典例剖析
考点透视
考场练兵
首尾顺次
n边形
相邻两边
延长线
n
n
n
n
D
考点透视
不相邻
7
C
相等
相等
同一侧
C
D
(n-2)×180°
C
C
360°
B
相等
相等
互补
十
C
平行四边形
ABCD
平行四边形
两组对边分别平行的四边形叫平行四边形
相等
相等
5cm
125°
55°
125°
互相平分
21
全等
相等
2
2
8
3<x<13
相等
相等
118°
互相平分
C
平行且相等
4
中点
平行
一半
3
B
直角
平行且相等
都是直角
互相平分且相等
2
等于斜边的一半
5
相等
B
三
C
邻边
两条对角线所在的直线
相等
互相垂直平分
平分
16
一半
24
有一组邻边相等
四条边相等
对角线互相垂直
四条边相等的四边形是菱形
直角
相等
互相垂直平分且相等
22.5°
相等
直角
矩形
菱形
D
一组对边平行而另一组对边不平行的四边形叫做梯形(trapezium).在梯形中,平行的两边叫做梯形的底(通常把较短的底叫做上底,较长的底叫做下底);不平行的两边叫做梯形的腰;两底之间的距离叫做梯形的高(如图 22 -46(1)).
如图 22 - 46(2)(3),有一个角是直角的梯形叫做直角梯形(right-angled trapezium);两腰相等的梯形叫做等腰梯形(isoscelestrapezium),它们都是特殊的梯形.
知识点27:梯形
自我诊断35.在直角梯形ABCD中,AD//BC, ∠ A=90°,
AD=10cm,DC=13cm,BC=15cm,求AB的长。
作高,将梯形问题转化成直角三角形和矩形.
解:作DE⊥BC于点E ,则∠DEB=90°
∵ AD//BC,
∴ ∠A+ ∠ B=180 °
∵ ∠A=90 °
∴ ∠B=90 °
∵ ∠A=90 °,∠B=90 °,∠DEB=90°
∴四边形ABED是矩形
∴AD= BE,AB=DE
∵AD=10cm,BC=15cm
∴EC=BC-BE=BC-AD=5cm
在Rt△DEC中,
∵ ∠DEC=90°
∴
∴AB=12cm
自我诊断36.如图,在梯形ABCD中,AB//CD,
∠D=2 ∠B,AD=10,AB=15,求CD的长。
平移一腰,将梯形问题转化成三角形和
平行四边形.
解:作CE //DA交AB于点E
∵ AB//DC, CE //DA
∴四边形AECD是平行四边形
∴CE=DA, DC=AE, ∠D= ∠ 1
∵AD=10 ,∠D= 2∠ B
∴CE=10, ∠1= 2∠ B
∵ ∠1= ∠ B+ ∠ 2
∴∠2= ∠ B
∴EB= EC=10
∵AB=15
∴AE=AB-EB=5
∴CD=5
E
1
2
知识点28:等腰梯形的三种判定方法:
①两腰相等的梯形是等腰梯形。
②同一底上的两个底角相等的梯形是等腰梯形。
③对角线相等的梯形是等腰梯形。
自我诊断37.已知:矩形ABCD中,点E、F在边AD上,AE=FD。
求证:四边形EBCF等腰梯形。
证明:∵ 四边形ABCD是矩形
∴ AB=DC,AD∥BC,
∠A=∠D=900
∵ AE=DF
∴ △ABE≌△DCF(SAS)
∴ EB=FC
又 ∵ EF∥BC,且EF≠BC,
∴四边形 EFCB是梯形
∴ 四边形EBCF是等腰梯形(两腰相等的梯形是等腰梯形)
A E F D
B C
梯形的中位线平行于两底,并且等于两底和的一半
知识点29:梯形中位线定理:
∵AD ∥BC
AM=MB,DN=NC
∴ MN ∥ BC
MN=(BC+AD)
(梯形的中位线平行于两底,并且等于两底和的一半)
自我诊断38.一个梯形的上底长4 cm,下底长6 cm,则其中位线长为 cm;
自我诊断39.一个梯形的上底长10 cm,中位线长16 cm,则其下底长为 cm;
5
22
向量:既有大小、又有方向的量.
几何表示:
有向线段
A
B
符号语言: ,
模: ,
位置向量
自由向量
相等向量
相反向量
平行向量
向量的模型——位移
从始点A出发到终点B的过程中的位移为 .
位移由运动过程中的始点和终点确定,而与运动的路径无关.
知识点30:平面向量
一、向量加法的运算(作图)法则:
二、向量减法的运算(作图)法则:
1、三角形法则,(起点和终点重合)
2、多边形形法则(首尾依次相连接)
1、三角形法则(共起点,尾相连)
3、平行四边形法则(共起点,做平行四边形)
2、平行四边形法则(共起点,做平行四边形)
以共起点为起点的对角线向量,就是a,b的和向量;
与被减向量共终点的对角线向量,就是a,b的差向量。
知识点31:平面向量的加减
自我诊断40.不画图怎样直接计算:
______________
______________
______________
“共”“起”点
“减”到“被”
向量减法的要领是什么?
A
C
典例剖析
不唯一,如DE=EC
32cm或34cm
C
AB=BC或AC⊥BD
A
B
易错易混
B
C
(3,2)或(-3,2)或(5,-2)
技巧1:特殊平行四边形的证明与计算
技巧总结
C
A
B
技巧2:四边形中的图形变换
C
B
5
6
40°
B
技巧3:解决梯形问题的基本思路和方法:
通过添加适当的辅助线,把梯形问题转化为平行四边形和三角形的问题来解决。
常画的辅助线有以下几种:
B
A
D
C
E
作一腰平行线
B
A
D
C
E
F
作高线
E
B
A
D
C
延长两腰
B
C
D
A
O
E
作对角线的平行线
1.一个多边形的内角和是540°,这个多边形是( ____ )
A.五边形
B.六边形
C.七边形
D.八边形
【解析】解:设多边形的边数是n,则
(n-2) 180°=540°,
解得n=5,
∴这个多边形是五边形,
故选:A.
A
考场练兵
2.下列等式中不正确的是( ____ )
A.
B.-(- )=
C.( + )+ = +( + )
D. +(- )= -
【解析】解:A、 ,符合题意;
B、-(- )= ,不符合题意;
C、( + )+ = +( + ),不符合题意;
A
D、 +(- )= - ,不符合题意.
故选:A.
3.如图,已知四边形ABCD是平行四边形,那么添加下列条件能判定四边形ABCD是正方形的是( ____ )
A.AB=AD且AC⊥BD
B.AC⊥BD且AC和BD互相平分
C.∠BAD=∠ABC且AC=BD
D.AC=BD且AB=AD
【解析】解:A、AB=AD且AC⊥BD,是菱形,不符合题意;
B、对角线互直垂直且互相平分,是菱形,不符合题意;
C、∠BAD=∠ABC且AC=BD不能判断四边形ABCD是正方形,不符合题意;
D
D、AC=BD且AB=AD四边相等,是正方形,符合题意;
故选:D.
4.已知梯形的四条边长分别是4、5、7、8,则中位线长可以为( ____ )
A.4.5 B.5.5 C.6 D.6.5
【解析】解:如图,过D作DE∥AB,∴BE=AD,AB=DE,
∵梯形的四条边长分别是4、5、7、8,
当梯形的两底长分别为4和8,腰分别为5和7,
即DE=5,BE=4,
C
∴CE=4,
∵4+5>7,∴DE,CE,CD能构成三角形,
∴中位线长= (4+8)=6,
当梯形的两底长分别为5和8,腰分别为4和7,DE,CE,CD不能构成三角形,其他情况也是一样,
综上所述,中位线长可以为6,故选:C.
5.如果O是正方形ABCD对角线AC、BD的交点,那么向量 、 、 、 是( ____ )
A.相等向量 B.相反向量
C.平行向量 D.模相等的向量.
【解析】解:∵O是正方形ABCD对角线AC、BD的交点,
∴OA=OC=OB=OD,
∴| |=| |=| |=| |,
D
∵ 、 、 、 的方向不同,
∴ 、 、 、 是模相等的量,
故选:D.
6.四边形不具有稳定性.四条边长都确定的四边形,当内角的大小发生变化时,其形状也随之改变.如图,改变正方形ABCD的内角,使正方形ABCD变为菱形ABC′D′,如果∠DAD′=30°,那么菱形ABC′D′与正方形ABCD的面积之比是( ____ )
A. B. C. D.1
A
【解析】解:过D'作D'M⊥AB于M,如图所示:则∠D'MA=90°,
∵四边形ABCD是正方形,∴正方形ABCD的面积=AB2,AB=AD,∠BAD=90°,
∵∠DAD′=30°,∴∠D'AM=90°-30°=60°,∴∠AD'M=30°,
∴AM= AD',D'M= AM= AD',
∵四边形ABC′D′是菱形,∴AB=AD'=AD,菱形ABCD的面积=AB×D'M= AB2,
∴菱形ABC′D′与正方形ABCD的面积之比= = ,故选:A.
7.如图,菱形ABCD的对角线的长分别为12和15,P是对角线AC上任一点(点P不与点A、C重合)且PE∥BC交AB于E,PF∥CD交AD于F,那么阴影部分的面积是 ____ .
【解析】解:设AP与EF相交于O点.∵四边形ABCD为菱形,
45
∴BC∥AD,AB∥CD.
∵PE∥BC,PF∥CD,
∴PE∥AF,PF∥AE.
∴四边形AEFP是平行四边形.
∴阴影部分的面积等于△ABC的面积.
∵△ABC的面积等于菱形ABCD的面积的一半,
∴菱形ABCD的面积= AC BD=90,
∴图中阴影部分的面积为90÷2=45.
故答案为:45.
8.已知菱形的周长为40,一条对角线长为12,则这个菱形的面积是 ____ .
【解析】解:因为周长是40,所以边长是10.
如图所示:AB=10,AC=12.
根据菱形的性质,AC⊥BD,AO=6,
∴BO=8,BD=16.
∴面积S= AC×BD=12×16× =96.
故答案为96.
96
9.如图,在等腰梯形ABCD中,AB∥CD,对角线AC⊥BC,∠B=60°,BC=6cm,则梯形ABCD的周长为 ____ .
【解析】解:∵在等腰梯形ABCD中,AB∥CD,
∴AD=BC=6,
∵AC⊥BC,∠B=60°,
∴∠BAC=30°,∠DAB=∠B=60°,
∴AB=2BC=12,∠DAC=30°,
∵AB∥CD,
∴∠DCA=∠BAC=30°,
30
∴∠DAC=∠DCA,
∴AD=CD=6,
∴等腰梯形的周长为:AB+BC+CD+AD=12+6+6+6=30.
故答案为:30.
10.如图,已知在△ABC中,点D是边AC的中点,设 ,用向量 、 表示向量 = .
【解析】解:∵点D是边AC的中点,
∴ ,
又∵ ,
∴ =- ,
故答案为:- .
11.如图,在 ABCD中,AE⊥BC、AF⊥CD,垂足分别为E、F,若∠B=50°,则∠FAE的度数是 _____ .
【解析】解:∵四边形ABCD是平行四边形,
∴AB∥CD,
∵∠B=50°,
∴∠C=180°-∠B=130°,
∵AE⊥BC、AF⊥CD,
∴∠AEC=∠AFC=90°,
∴∠FAE=360°-∠AEC-∠AFC-∠C=50°,
故答案为:50°.
50°
12.一个多边形的内角和是2880°,则这个多边形是 ____ 边形.
【解析】解:设这个多边形是n边形,根据题意,得
(n-2)×180°=2880°,
∴n=18.
故答案为:18.
18
13.我们把对角线与一边垂直的平行四边形叫做“优美平行四边形”.如果一个“优美平行四边形”的一组邻边长为 和4,那么它的最大的内角为 _____ 度.
【解析】解:如图所示:
在平行四边形ABCD中,AB⊥AC,AB=2 ,BC=4时,∠BAD最大;
由勾股定理得:AC= =2 ,
∴AC=AB,
∴∠B=45°,
135
∴∠BAD=180°-∠B=135°.
故答案为:135.
14.如图,已知平行四边形ABCD的对角线AC、BD相交于点O,OE⊥AC交AD边于点E,若△EDC的周长为15厘米,则平行四边形ABCD的周长为 ____ 厘米.
【解析】解:∵四边形ABCD是平行四边形,
∴O点为AC中点.
∵OE⊥AC,
∴AE=CE.
∴△EDC的周长=CD+CE+DE=CD+AE+DE=CD+AD=15.
∴平行四边形ABCD周长为2×15=30.
30
故答案为:30.
15.如图,梯形ABCD中,AD∥BC,∠BAC=90°,AB=AC,对角线AC与BD相交于点O,且BD=BC,那么∠AOB= ____ 度.
【解析】解:如图,作AF⊥BC于F,DE⊥BC于E,
在Rt△ABC中,
∵AB=AC,∠BAC=90°,
∴∠ABC=∠ACB=45°,
∴BC= AB,AF= AB,
∴AF= BC.
75
又∵DE=AF,
∴DE= BC= BD,
∴ = ,
∴sin∠1= ,
∴∠1=30°,
∴∠BOC=180°-30°-45°=105°,
∴∠AOB=180°-∠BOC=180°-105°=75°,
故答案为:75.
16.如图,在梯形ABCD中,AB∥CD,点E、F分别是AD、BC的中点,如果AB=2,EF=3,那么CD= ____ .
【解析】解:在梯形ABCD中,AB∥CD,点E、F分别是AD、BC的中点,
∴EF是梯形ABCD的中位线,
∴EF= (AB+CD),
∴CD=2EF-AB=6-2=4.
故答案为:4.
4
17.如图,在Rt△ABC中,∠BAC=90°,AD是△ABC的中线,点E,F分别是AD,AC的中点,连接EF,若EF=3,则AD的长为 ____ .
【解析】解:∵点E,F分别是AD,AC的中点,
∴EF是△ACD的中位线,
∴ ,
∴CD=6,
∵∠BAC=90°,AD是△ABC的中线,
∴AD=CD=6.
故答案为:6.
6
18.对于任意三角形,如果存在一个菱形,使得这个菱形的一条边与三角形的一条边重合,且三角形的这条边所对的顶点在菱形的这条边的对边上,那么称这个菱形为该三角形的“最优覆盖菱形”.
问题:如图,在△ABC中,AB=AC,BC=4,且△ABC的面积为m.如果△ABC存在“最优覆盖菱形”为菱形BCMN,那么m的取值范围 .
【解析】解:∵△ABC的面积为m,
∴△ABC的BC边上的为高 ,
如图:当高取最小值时,△ABC为等边三角形,
点A与M或N重合,
____
如图:过A作AD⊥BC,垂足为D
∵等边三角形ABC,BC=4,
∴∠ABC=60°,BC=4,∠BAD=30°.
∴BD=2,
∴AD= BD=2 ,
∴ =2 ,即m=4 .
如图:
___
当高取最大值时,菱形为正方形,
∴点A在MN的中点,∴ =4,
∴m=8,∴4 ≤m≤8,
故答案为:4 ≤m≤8.
19.如图,已知在平行四边形ABCD中,∠BAD的角平分线AE交CD于点F,交BC的延长线于点E.
(1)求证:BE=CD;
(2)若BF恰好平分∠ABE,连接AC、DE,求证:四边形ACED是平行四边形.
【解析】证明:(1)∵四边形ABCD是平行四边形,
∴AD∥BC,AB=CD,∴∠DAE=∠AEB,
∵AE平分∠BAD,∴∠BAE=∠DAE,
∴∠BAE=∠AEB,
∴BE=AB,
∴BE=CD;
(2)∵BE=AB,BF平分∠ABE,
∴AF=EF,
在△ADF和△ECF中,
,
∴△ADF≌△ECF(ASA),
∴DF=CF,
又∵AF=EF,
∴四边形ACED是平行四边形.
20.已知:如图矩形ABCD中,AC和BD相交于点O,设 , .
(1)填空: = ;(用a、b的式子表示)
(2)在图中求作 .
(不要求写出作法,只需写出结论即可.)
【解析】解:(1)∵ , , ,
∴ = ,
故答案为: ;
(2)如图所示, 即为所求;
__
21.如图,已知在△ABC中,AB=AC,点O是△ABC内任意一点,点D、G、E、F分别是AB,AC,OB,OC的中点.
(1)求证:四边形DEFG是平行四边形;
(2)若∠A=2∠BDE,求证:四边形DEFG是矩形.
【解析】证明:(1)∵点D、G、E、F分别是AB,AC,OB,OC的中点,
∴DG是△ABC的中位线,
∴DG∥BC,DG= BC,
同理:EF∥BC,EF= BC,
∴DG∥EF,DG=EF,
∴四边形DEFG是平行四边形;
(2)∵点D、E、F、G分别是AB、AC、OB、OC的中点,
∴DG是△ABC的中位线,EF是△OBC的中位线,
∴DG∥BC,DG= BC,EF∥BC,EF= BC,
∴∠ADG=∠ABC,∠AGD=∠ACB,DG∥EF,DG=EF,
∴四边形DEGF是平行四边形,
∵AB=AC,∴∠ABC=∠ACB,
∴∠ADG=∠AGD,
∵∠ADG+∠AGD+∠A=180°,即2∠ADG+∠A=180°,
∴∠ADG+ ∠A=90°,
∵∠A=2∠BDE,∴∠BDE= ∠A,
∴∠ADG+∠BDE=90°,
∴∠EDG=180°-∠ADG-∠BDE=180°-90°=90°,
∴四边形DEFG是矩形.
22.如图,已知 ABCD,过点D作DE⊥BC交CB延长线于点E,过点C作CF∥DE交AD的延长线于点F.
(1)求证:四边形DECF是矩形;
(2)设DE边与AB相交于点G,连结CG、BD,若CG=BD,求证:∠FDC=∠BGE.
【解析】证明:(1)∵四边形ABCD是平行四边形,
∴AD∥BC,
∵CF∥DE,
∴四边形DECF是平行四边形,
∵DE⊥BC,
∴∠DEC=90°,
∴四边形DECF是矩形;
(2)如图,
____
∵BG∥CD,CG=BD,
∴四边形DGBC为等腰梯形,
∴DG=CB,
∵AD=BC,
∴AD=DG,
∵∠ADG=∠FDG=90°,
∴∠DAG=∠DGA=45°,
∴∠BGE=∠DGA=45°,
∵AB∥DC,
∴∠CDG=∠DGA=45°,
∴∠FDC=∠FDE-∠CDG=90°-45°=45°,
∴∠FDC=∠BGE.
