7.2.2复数的乘、除运算 学案
文档属性
| 名称 | 7.2.2复数的乘、除运算 学案 |

|
|
| 格式 | doc | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-04-18 13:19:14 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
7.2.2复数的乘、除运算
班级 姓名
学习目标
1.掌握复数的乘法和除法运算.
2.理解复数乘法的交换律、结合律和乘法对加法的分配律.
学习过程
自学指导 自学检测及课堂展示
阅读教材,完成右边的内容 一、复数的乘法1.复数代数形式的乘法法则已知z1=a+bi,z2=c+di(a,b,c,d∈R),则z1·z2=(a+bi)(c+di)= .2.复数乘法的运算律对于任意z1,z2,z3∈C,有交换律z1·z2=z2·z1结合律(z1·z2)·z3= 乘法对加法的分配律z1(z2+z3)= 【即时训练1】(1)复数(3+2i)i等于 .(2)已知复数(a+2i)(1+i)的实部为0,其中i为虚数单位,则实数a的值是____.
阅读教材,完成右边的内容 二、复数的除法法则(a+bi)÷(c+di)=+i(a,b,c,d∈R,且c+di≠0).【即时训练2】已知i是虚数单位,则= .
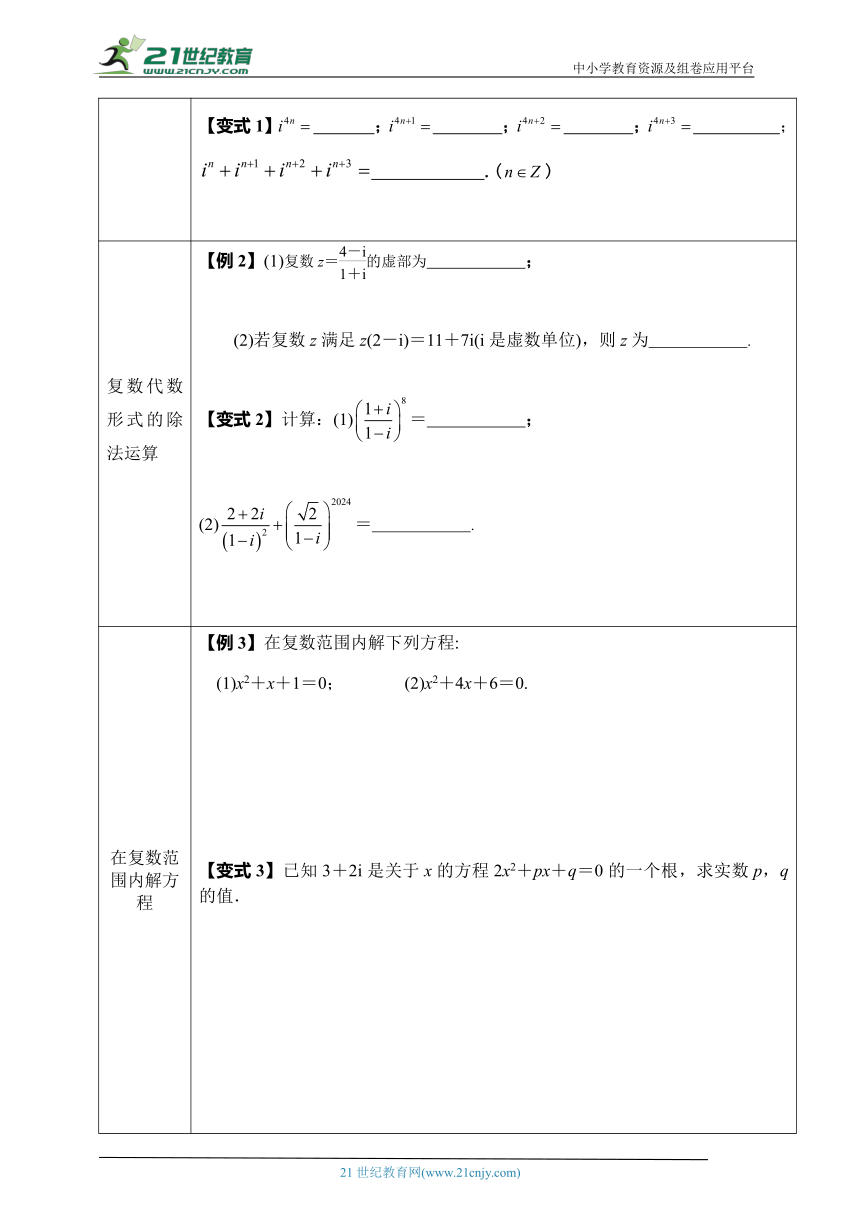
复数代数形式的乘法运算 【例1】计算:(1)(2+3i)(2-3i); (2)(1+i)2; (3)(-2-i)(3-2i)(-1+3i).【变式1】 ; ; ; ; .()
复数代数形式的除法运算 【例2】(1)复数z=的虚部为 ;(2)若复数z满足z(2-i)=11+7i(i是虚数单位),则z为 .【变式2】计算:(1)= ;(2)= .
在复数范围内解方程 【例3】在复数范围内解下列方程:(1)x2+x+1=0; (2)x2+4x+6=0.【变式3】已知3+2i是关于x的方程2x2+px+q=0的一个根,求实数p,q的值.
课后作业
一、基础训练题
1.=( )
A.1+i B.1-i C.-1+i D.-1-i
2.如图,在复平面内,复数z1,z2对应的向量分别是,,则复数对应的点位于( )
A.第一象限 B.第二象限
C.第三象限 D.第四象限
3.设复数z的共轭复数是,若复数z1=3+4i,z2=t+i,且z1·2是实数,则实数t等于( )
A. B. C.- D.-
4.已知复数z=,则复数z在复平面内对应的点位于( )
A.第一象限 B.第二象限
C.第三象限 D.第四象限
5.(多选题)下面是关于复数z=(i为虚数单位)的命题,其中真命题为( )
A.|z|=2 B.z2=2i
C.z的共轭复数为1+i D.z的虚部为-1
6.已知=b+i(a,b∈R),其中i为虚数单位,则a+b=________.
7.在复数范围内,方程x2+6x+10=0的根为x=________.
8.计算:(1)+; (2);
(3)++.
9.已知复数z满足(1+i)z=1-3i(i是虚数单位).
(1)求复数z的虚部;
(2)若复数(1+ai)z是纯虚数,求实数a的值;
(3)若复数z的共轭复数为,求复数的模.
10.已知x=-1+i是方程x2+ax+b=0(a,b∈R)的一个根.
(1)求实数a,b的值;
(2)结合根与系数的关系,猜测方程的另一个根,并给予证明.
二、综合训练题
11.(多选题)设z为复数,则下列命题中正确的是( )
A.|z|2=z
B.z2=|z|2
C.若|z|=1,则|z+i|的最大值为2
D.若|z-1|=1,则0≤|z|≤2
12.若z1=a+2i,z2=3-4i,且为纯虚数,则实数a的值为________,z1z2=________.
7.2.2复数的乘、除运算
参考答案
1、【答案】D
【解析】==-1-i,选D.
2、【答案】B
【解析】由复数的几何意义知,z1=-2-i,z2=i,
所以==-1+2i,对应的点在第二象限.
3、【答案】A
【解析】∵z2=t+i,∴2=t-i.z1·2=(3+4i)(t-i)=3t+4+(4t-3)i,
又∵z1·2∈R,∴4t-3=0,∴t=.
4、【答案】A
【解析】i+i2+i3+i4=i-1-i+1=0,i5+i6+i7+i8=i+i2+i3+i4=0,
所以i+i2+i3+i4+…+i2025=i.
所以z===+i,所以对应点在第一象限,故选A.
5、【答案】BD
【解析】∵z===-1-i,
∴|z|=,A错误;z2=2i,B正确;
z的共轭复数为-1+i,C错误;
z的虚部为-1,D正确.故选BD.
6、【答案】1
【解析】∵=b+i,∴a+2i=(b+i)i=-1+bi,
∴a=-1,b=2,∴a+b=1.
7、【答案】-3±i
【解析】因为b2-4ac=62-4×1×10=-4<0,
所以x====-3±i.
8、【解】(1)+=+=i-i=0.
(2)===
==-2-2i.
(3)原式=+1012+=i+(-i)1012+=i+1+0=1+i.
9、【解】(1)由(1+i)z=1-3i,得z====-1-2i,
∴复数z的虚部为-2.
(2)(1+ai)z=(1+ai)(-1-2i)=2a-1-(2+a)i,
∵复数(1+ai)z是纯虚数,∴解得a=.∴实数a的值为.
(3)由z=-1-2i,得=-1+2i.
则====-1-i,∴|z|==.
∴复数的模为.
10、【解】(1)把x=-1+i代入方程x2+ax+b=0,得(-a+b)+(a-2)i=0,
∴解得a=2,b=2.
(2)由(1)知方程为x2+2x+2=0.设另一个根为x2,由根与系数的关系,得-1+i+x2=-2,∴x2=-1-i.
把x2=-1-i代入方程x2+2x+2=0,则左边=(-1-i)2+2(-1-i)+2=0=右边,
∴x2=-1-i是方程的另一个根
11、【答案】ACD
【解析】对于A∶z=a+bi(a,b∈R,则=a-bi,∴|z|2=a2+b2,
而z=a2+b2,所以|z|2=z成立;
对于B∶z=a+bi(a,b∈R),当ab均不为0时,z2=(a+bi)2=a2-b2+2abi,
而|z|2=a2+b2,所以z2=|z|2不成立;
对于C∶|z|=1可以看出以O(0,0)为圆心,1为半径的圆上的点P,
|z+i|可以看成点P到Q(0,-1)的距离,所以当P(0,1)时,可取|z+i|的最大值为2;
对于D∶|z-1|=1可以看出以M(1,0)为圆心,1为半径的圆上的点N,
则|z|表示点N到原点距离,故O,N重合时,|z|=0最小,
当O,M,N三点共线时,|z|=2最大,故0≤|z|≤2.
12、【答案】 16-i
【解析】====,
∵为纯虚数,∴∴a=.
∴z1·z2=(3-4i)=8-i+6i+8=16-i.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
7.2.2复数的乘、除运算
班级 姓名
学习目标
1.掌握复数的乘法和除法运算.
2.理解复数乘法的交换律、结合律和乘法对加法的分配律.
学习过程
自学指导 自学检测及课堂展示
阅读教材,完成右边的内容 一、复数的乘法1.复数代数形式的乘法法则已知z1=a+bi,z2=c+di(a,b,c,d∈R),则z1·z2=(a+bi)(c+di)= .2.复数乘法的运算律对于任意z1,z2,z3∈C,有交换律z1·z2=z2·z1结合律(z1·z2)·z3= 乘法对加法的分配律z1(z2+z3)= 【即时训练1】(1)复数(3+2i)i等于 .(2)已知复数(a+2i)(1+i)的实部为0,其中i为虚数单位,则实数a的值是____.
阅读教材,完成右边的内容 二、复数的除法法则(a+bi)÷(c+di)=+i(a,b,c,d∈R,且c+di≠0).【即时训练2】已知i是虚数单位,则= .
复数代数形式的乘法运算 【例1】计算:(1)(2+3i)(2-3i); (2)(1+i)2; (3)(-2-i)(3-2i)(-1+3i).【变式1】 ; ; ; ; .()
复数代数形式的除法运算 【例2】(1)复数z=的虚部为 ;(2)若复数z满足z(2-i)=11+7i(i是虚数单位),则z为 .【变式2】计算:(1)= ;(2)= .
在复数范围内解方程 【例3】在复数范围内解下列方程:(1)x2+x+1=0; (2)x2+4x+6=0.【变式3】已知3+2i是关于x的方程2x2+px+q=0的一个根,求实数p,q的值.
课后作业
一、基础训练题
1.=( )
A.1+i B.1-i C.-1+i D.-1-i
2.如图,在复平面内,复数z1,z2对应的向量分别是,,则复数对应的点位于( )
A.第一象限 B.第二象限
C.第三象限 D.第四象限
3.设复数z的共轭复数是,若复数z1=3+4i,z2=t+i,且z1·2是实数,则实数t等于( )
A. B. C.- D.-
4.已知复数z=,则复数z在复平面内对应的点位于( )
A.第一象限 B.第二象限
C.第三象限 D.第四象限
5.(多选题)下面是关于复数z=(i为虚数单位)的命题,其中真命题为( )
A.|z|=2 B.z2=2i
C.z的共轭复数为1+i D.z的虚部为-1
6.已知=b+i(a,b∈R),其中i为虚数单位,则a+b=________.
7.在复数范围内,方程x2+6x+10=0的根为x=________.
8.计算:(1)+; (2);
(3)++.
9.已知复数z满足(1+i)z=1-3i(i是虚数单位).
(1)求复数z的虚部;
(2)若复数(1+ai)z是纯虚数,求实数a的值;
(3)若复数z的共轭复数为,求复数的模.
10.已知x=-1+i是方程x2+ax+b=0(a,b∈R)的一个根.
(1)求实数a,b的值;
(2)结合根与系数的关系,猜测方程的另一个根,并给予证明.
二、综合训练题
11.(多选题)设z为复数,则下列命题中正确的是( )
A.|z|2=z
B.z2=|z|2
C.若|z|=1,则|z+i|的最大值为2
D.若|z-1|=1,则0≤|z|≤2
12.若z1=a+2i,z2=3-4i,且为纯虚数,则实数a的值为________,z1z2=________.
7.2.2复数的乘、除运算
参考答案
1、【答案】D
【解析】==-1-i,选D.
2、【答案】B
【解析】由复数的几何意义知,z1=-2-i,z2=i,
所以==-1+2i,对应的点在第二象限.
3、【答案】A
【解析】∵z2=t+i,∴2=t-i.z1·2=(3+4i)(t-i)=3t+4+(4t-3)i,
又∵z1·2∈R,∴4t-3=0,∴t=.
4、【答案】A
【解析】i+i2+i3+i4=i-1-i+1=0,i5+i6+i7+i8=i+i2+i3+i4=0,
所以i+i2+i3+i4+…+i2025=i.
所以z===+i,所以对应点在第一象限,故选A.
5、【答案】BD
【解析】∵z===-1-i,
∴|z|=,A错误;z2=2i,B正确;
z的共轭复数为-1+i,C错误;
z的虚部为-1,D正确.故选BD.
6、【答案】1
【解析】∵=b+i,∴a+2i=(b+i)i=-1+bi,
∴a=-1,b=2,∴a+b=1.
7、【答案】-3±i
【解析】因为b2-4ac=62-4×1×10=-4<0,
所以x====-3±i.
8、【解】(1)+=+=i-i=0.
(2)===
==-2-2i.
(3)原式=+1012+=i+(-i)1012+=i+1+0=1+i.
9、【解】(1)由(1+i)z=1-3i,得z====-1-2i,
∴复数z的虚部为-2.
(2)(1+ai)z=(1+ai)(-1-2i)=2a-1-(2+a)i,
∵复数(1+ai)z是纯虚数,∴解得a=.∴实数a的值为.
(3)由z=-1-2i,得=-1+2i.
则====-1-i,∴|z|==.
∴复数的模为.
10、【解】(1)把x=-1+i代入方程x2+ax+b=0,得(-a+b)+(a-2)i=0,
∴解得a=2,b=2.
(2)由(1)知方程为x2+2x+2=0.设另一个根为x2,由根与系数的关系,得-1+i+x2=-2,∴x2=-1-i.
把x2=-1-i代入方程x2+2x+2=0,则左边=(-1-i)2+2(-1-i)+2=0=右边,
∴x2=-1-i是方程的另一个根
11、【答案】ACD
【解析】对于A∶z=a+bi(a,b∈R,则=a-bi,∴|z|2=a2+b2,
而z=a2+b2,所以|z|2=z成立;
对于B∶z=a+bi(a,b∈R),当ab均不为0时,z2=(a+bi)2=a2-b2+2abi,
而|z|2=a2+b2,所以z2=|z|2不成立;
对于C∶|z|=1可以看出以O(0,0)为圆心,1为半径的圆上的点P,
|z+i|可以看成点P到Q(0,-1)的距离,所以当P(0,1)时,可取|z+i|的最大值为2;
对于D∶|z-1|=1可以看出以M(1,0)为圆心,1为半径的圆上的点N,
则|z|表示点N到原点距离,故O,N重合时,|z|=0最小,
当O,M,N三点共线时,|z|=2最大,故0≤|z|≤2.
12、【答案】 16-i
【解析】====,
∵为纯虚数,∴∴a=.
∴z1·z2=(3-4i)=8-i+6i+8=16-i.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
同课章节目录
- 第六章 平面向量及其应用
- 6.1 平面向量的概念
- 6.2 平面向量的运算
- 6.3 平面向量基本定理及坐标表示
- 6.4 平面向量的应用
- 第七章 复数
- 7.1 复数的概念
- 7.2 复数的四则运算
- 7.3 * 复数的三角表示
- 第八章 立体几何初步
- 8.1 基本立体图形
- 8.2 立体图形的直观图
- 8.3 简单几何体的表面积与体积
- 8.4 空间点、直线、平面之间的位置关系
- 8.5 空间直线、平面的平行
- 8.6 空间直线、平面的垂直
- 第九章 统计
- 9.1 随机抽样
- 9.2 用样本估计总体
- 9.3 统计分析案例 公司员工
- 第十章 概率
- 10.1 随机事件与概率
- 10.2 事件的相互独立性
- 10.3 频率与概率
