人教版四年级上册数学平行四边形复习课件(共22张PPT)
文档属性
| 名称 | 人教版四年级上册数学平行四边形复习课件(共22张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 858.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-04-17 00:00:00 | ||
图片预览






文档简介
(共22张PPT)
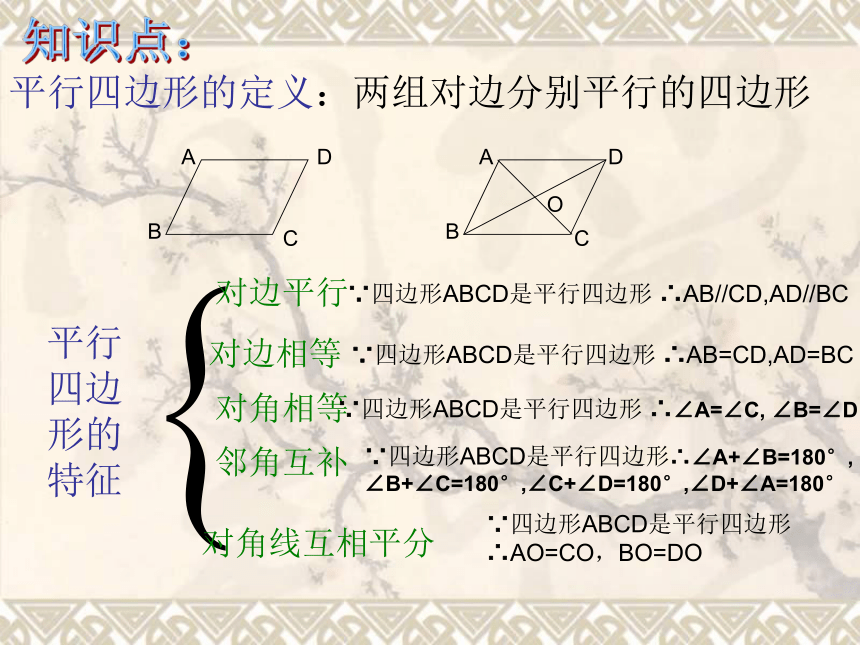
四边形 复行四边形的定义:两组对边分别平行的四边形
平行四边形的特征
对边平行
对边相等
对角相等
邻角互补
对角线互相平分
∵四边形ABCD是平行四边形 ∴AB//CD,AD//BC
∵四边形ABCD是平行四边形 ∴AB=CD,AD=BC
∵四边形ABCD是平行四边形 ∴∠A=∠C, ∠B=∠D
∵四边形ABCD是平行四边形∴∠A+∠B=180°,
∠B+∠C=180°,∠C+∠D=180°,∠D+∠A=180°
∵四边形ABCD是平行四边形
∴AO=CO,BO=DO
A
B
C
D
A
B
C
D
O
知识点:
矩形
矩形的定义:有一个角是直角的平行四边形。
矩形的特征
具有平行四边形的一切特征
四个角都是直角
对角线相等且平分
菱形
菱形的定义:有一组邻边相等的平行四边形。
菱形的特征
具有平行四边形的一切特征
四条边相等
对角线互相垂直平分
对角线分别平分两组对角
正方形
正方形的定义:有一组邻边相等且有一个角是直角的平行四边形。
正方形的特征
四条边相等
对角线互相垂直平分且相等
对角线分别平分两组对角
对边平行
四个角都是直角
梯形
梯形的定义:一组对边平行而另一组对边不平行的四边形
等腰梯形的特征
两腰相等
对角线相等
两底平行
同一底上的两个内角相等
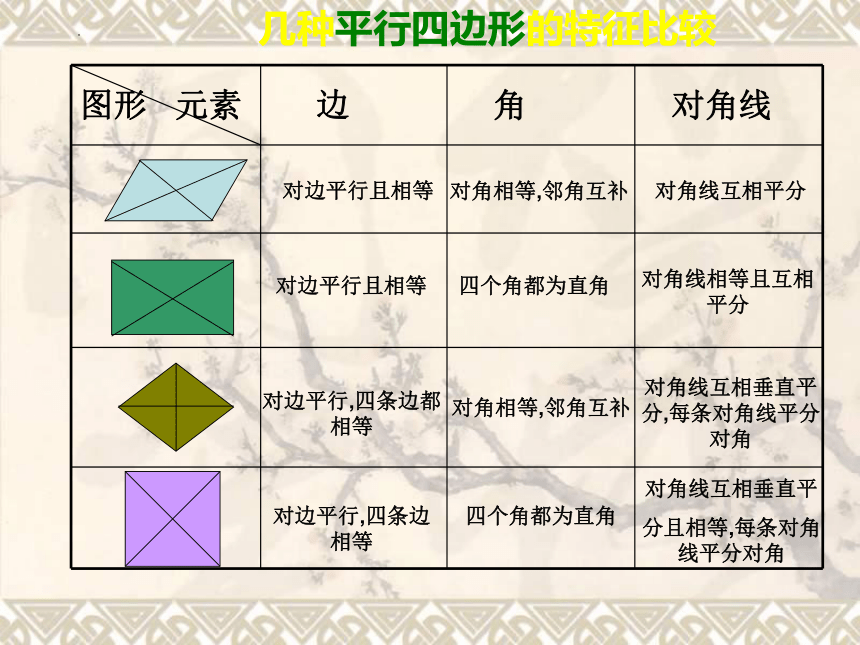
几种平行四边形的特征比较
图形 元素 边 角 对角线
对边平行且相等
对边平行且相等
对边平行,四条边都
相等
对边平行,四条边
相等
对角相等,邻角互补
四个角都为直角
对角相等,邻角互补
四个角都为直角
对角线互相平分
对角线相等且互相
平分
对角线互相垂直平
分,每条对角线平分
对角
对角线互相垂直平
分且相等,每条对角线平分对角
几种特殊四边形的特征
平行
四边形
矩 形
菱 形
正方形
等腰梯形
边
对边平行
且相等
对边平行
且相等
对边平行,四
条边都相等
对边平行,
四条边
都相等
两底平行,
两腰相等
角
对角相等
四个角
都是直角
对角相等
四个角
都是直角
同一底上的
两个角相等
对 角 线
两条对角线互相平分
两条对角线互相平分且相等
两条对角线互相垂直平分,
每条对角线平分一组对角
两条对角线互相垂直平分
且相等,每条对角线平分
一组对角
两条对角线相等
对称性
中心对称
轴对称(2条)
中心对称
轴对称(2条)
中心对称
轴对称(4条)
中心对称
轴对称(1条)
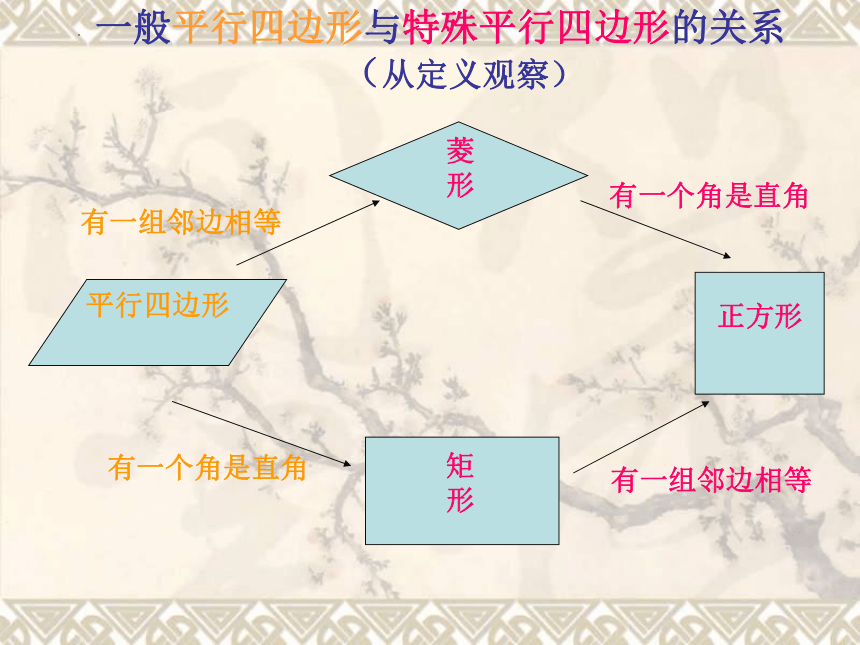
一般平行四边形与特殊平行四边形的关系
(从定义观察)
正方形
矩形
菱形
平行四边形
有一个角是直角
有一组邻边相等
有一组邻边相等
有一个角是直角
练一练1.
1、在 ABCD中,已知AB=8,AO=3,∠B=50°
则CD=________,AC=________
∠A=________, ∠D=___________
A
B
C
D
A
B
C
D
O
2、在 ABCD中, ∠A+ ∠C= 150°那么
∠A=__________,∠D=_________
3、在 ABCD中, ∠A:∠B= 4:5,那么
∠B=__________,∠C=_________
4、请在横线上写出结论,在括号里填理由
∵四边形ABCD是平行四边形
∴_________________( )
8
130°
6
75°
50°
105°
80°
100°
平行四边形的特征(5个,详见前知识点)
A
C
D
O
B
1、如图,在矩形ABCD中,AC、BD相交于点O, ∠AOB= 60°,AB=6,则AC=_______
练一练2.
2、已知矩形的周长是24,相邻两边之比是1:2,那么这个矩形的面积是_____________
3、矩形的两条对角线的夹角为60°,一条对角线与短边的和为15,则短边长为____________
A
C
D
O
B
4、请在横线上写出原因,在括号里填理由
∵四边形ABCD是矩形
∴____________________ ( )
5、(1)矩形具有而一般的平行四边形不具有的性质是( )
A、对角相等 B、对边相等
C、对角线相等 D、对角线互相平分
(2)把一张长方形的纸条按图那样折叠,若得到
∠AME=70o ,则∠EMN=( )
A、45o B、50o
C、55o D、60o
(3)如图,矩形ABCD沿AE折叠,使D点落在BC边上的F点处,
如果∠BAF=60°,那么∠DAE等于( )
A.15° B.30°
C.45° D.60°
A
B
C
D
O
1、如图,在菱形ABCD中,AB=10,OA=8,OB=6,则菱形的周长是_________,面积是___________
2、如图,在菱形ABCD中, ∠B= 120°,则
∠DAC=___________
A
B
C
D
A
B
C
D
3、菱形的一个内角为120°,较短的对角线长为10,那么菱形的周长是_____________
96
40
30°
40
练一练3.
4、(1)菱形有而一般的平行四边形不具有的性质是( )
A、对角相等 B、对角线互相平分
C、对边平行且相等 D、对角线互相垂直
(2)如图,小强拿一张正方形的纸(图(1)),沿虚线对折
一次得图(2),再对折一次得图(3),然后用剪刀沿图(3)
中的虚线剪成两部分,再把所得的三角形的部分打开后的
形状一定是( )
A.一般的平行四边形 B、菱形 C、矩形 D、正方形
(1)
(2)
(3)
练一练4.
A
O
D
C
B
1、如图,已知正方形ABCD对角线交于点O,则∠BOC=________
2、如图,以定点A、B为其中两个顶点作为正方形,一共可以作( )
A、4个 B、3个 C、2个 D、1个
A
B
B
90°
练一练5.
1、在直角梯形ABCD中, ∠ C=∠D=90°,且∠ A:∠B=1:3,那么∠ A=_____________
2、在四边形ABCD中, 若∠ A:∠B :∠ C:∠D=2:2:1:3,则这个四边形是________________
A
B
C
D
3、在等腰梯形ABCD中,BD⊥DC,且∠C=60°,
若AD=5㎝,则梯形的腰长为____________㎝
4、在梯形ABCD中,AB//DC,将BC平移到ED的位置,
若∠A=55°,∠C=120°,则∠ADE等于____________
D
A
B
C
E
45°
65°
5
直角梯形
小测验 一、判断题:
(1)一组对边平行,另一组对边相等的四边形
是平行四边形。
(2)对角线相等的四边形是矩形。
(3)对角线互相垂直的四边形
是平行四边形。
(4)对角线相等且互相垂直的四边形
是正方形。
(5)连结矩形各边中点所得的四边形
是菱形。
动手动脑,小组探究。
1、将矩形纸片ABCD、沿对角线AC折叠,
使B点落在E处。则EF与DF有什么关系?
试证明你的结论。
A
B
C
D
E
F
答:EF与DF是相等关系
证明:矩形ABCD中:
∵ ∠B=∠E=∠D =90°
AB=AE=CD
又∵∠ AFE=∠CFD
∴ ΔAEF ≌ ΔCDF(AAS)
∴EF=DF
(全等三角形对应边相等)
二、 填空题:
1、 ABCD的对角线AC与BD交于O,若
S ABCD=12cm , S AOB=_______。
2、矩形对角线的交角为60°,一条对角线与
较短边的和为18cm, 则对角线长是______。
3、菱形的周长为16,高为2,则菱形相
邻的两角的 度数大小为______________。
4、菱形的对角线长为10和24,则周长
为_________。
5、正方形ABCD中,E为BC上一点,且EF⊥
BD于F, 那么 △EFB是_______三角形。
3cm
30°、150°
12cm
52
等腰直角
2.正方形ABCD的对角线相交于点O ,点 O是正方形
MNPO的一个顶点,如果两个正方形的边长相等,那么
正方形MNPO绕点 怎样转动,试猜想两个正方形重叠
部分的面积四边形OEAF与正方形的面积有什么关系?
并证明你的结论。
0
A
B
C
D
A
M
N
P
E
F
答:SOEAF =
SABCD
有谁证明?
A
B
C
D
O
E
F
证明:正方形ABCD中:
∵ ∠EDO=∠ FAO=45°
DO=AO
∠ 1=90°–∠ 3=∠ 2
∴ △ DOE≌ △ AOF(ASA)
又∵ S四边形EAFO=S△ OEA+S△ AOF
∴ S四边形EAFO= S△ OEA +S△DOE
= S△ AOD = SABCD
1
2
3
(
(
(
45°
45°
同学们努力呵!
只有多练才有提高!
四边形 复行四边形的定义:两组对边分别平行的四边形
平行四边形的特征
对边平行
对边相等
对角相等
邻角互补
对角线互相平分
∵四边形ABCD是平行四边形 ∴AB//CD,AD//BC
∵四边形ABCD是平行四边形 ∴AB=CD,AD=BC
∵四边形ABCD是平行四边形 ∴∠A=∠C, ∠B=∠D
∵四边形ABCD是平行四边形∴∠A+∠B=180°,
∠B+∠C=180°,∠C+∠D=180°,∠D+∠A=180°
∵四边形ABCD是平行四边形
∴AO=CO,BO=DO
A
B
C
D
A
B
C
D
O
知识点:
矩形
矩形的定义:有一个角是直角的平行四边形。
矩形的特征
具有平行四边形的一切特征
四个角都是直角
对角线相等且平分
菱形
菱形的定义:有一组邻边相等的平行四边形。
菱形的特征
具有平行四边形的一切特征
四条边相等
对角线互相垂直平分
对角线分别平分两组对角
正方形
正方形的定义:有一组邻边相等且有一个角是直角的平行四边形。
正方形的特征
四条边相等
对角线互相垂直平分且相等
对角线分别平分两组对角
对边平行
四个角都是直角
梯形
梯形的定义:一组对边平行而另一组对边不平行的四边形
等腰梯形的特征
两腰相等
对角线相等
两底平行
同一底上的两个内角相等
几种平行四边形的特征比较
图形 元素 边 角 对角线
对边平行且相等
对边平行且相等
对边平行,四条边都
相等
对边平行,四条边
相等
对角相等,邻角互补
四个角都为直角
对角相等,邻角互补
四个角都为直角
对角线互相平分
对角线相等且互相
平分
对角线互相垂直平
分,每条对角线平分
对角
对角线互相垂直平
分且相等,每条对角线平分对角
几种特殊四边形的特征
平行
四边形
矩 形
菱 形
正方形
等腰梯形
边
对边平行
且相等
对边平行
且相等
对边平行,四
条边都相等
对边平行,
四条边
都相等
两底平行,
两腰相等
角
对角相等
四个角
都是直角
对角相等
四个角
都是直角
同一底上的
两个角相等
对 角 线
两条对角线互相平分
两条对角线互相平分且相等
两条对角线互相垂直平分,
每条对角线平分一组对角
两条对角线互相垂直平分
且相等,每条对角线平分
一组对角
两条对角线相等
对称性
中心对称
轴对称(2条)
中心对称
轴对称(2条)
中心对称
轴对称(4条)
中心对称
轴对称(1条)
一般平行四边形与特殊平行四边形的关系
(从定义观察)
正方形
矩形
菱形
平行四边形
有一个角是直角
有一组邻边相等
有一组邻边相等
有一个角是直角
练一练1.
1、在 ABCD中,已知AB=8,AO=3,∠B=50°
则CD=________,AC=________
∠A=________, ∠D=___________
A
B
C
D
A
B
C
D
O
2、在 ABCD中, ∠A+ ∠C= 150°那么
∠A=__________,∠D=_________
3、在 ABCD中, ∠A:∠B= 4:5,那么
∠B=__________,∠C=_________
4、请在横线上写出结论,在括号里填理由
∵四边形ABCD是平行四边形
∴_________________( )
8
130°
6
75°
50°
105°
80°
100°
平行四边形的特征(5个,详见前知识点)
A
C
D
O
B
1、如图,在矩形ABCD中,AC、BD相交于点O, ∠AOB= 60°,AB=6,则AC=_______
练一练2.
2、已知矩形的周长是24,相邻两边之比是1:2,那么这个矩形的面积是_____________
3、矩形的两条对角线的夹角为60°,一条对角线与短边的和为15,则短边长为____________
A
C
D
O
B
4、请在横线上写出原因,在括号里填理由
∵四边形ABCD是矩形
∴____________________ ( )
5、(1)矩形具有而一般的平行四边形不具有的性质是( )
A、对角相等 B、对边相等
C、对角线相等 D、对角线互相平分
(2)把一张长方形的纸条按图那样折叠,若得到
∠AME=70o ,则∠EMN=( )
A、45o B、50o
C、55o D、60o
(3)如图,矩形ABCD沿AE折叠,使D点落在BC边上的F点处,
如果∠BAF=60°,那么∠DAE等于( )
A.15° B.30°
C.45° D.60°
A
B
C
D
O
1、如图,在菱形ABCD中,AB=10,OA=8,OB=6,则菱形的周长是_________,面积是___________
2、如图,在菱形ABCD中, ∠B= 120°,则
∠DAC=___________
A
B
C
D
A
B
C
D
3、菱形的一个内角为120°,较短的对角线长为10,那么菱形的周长是_____________
96
40
30°
40
练一练3.
4、(1)菱形有而一般的平行四边形不具有的性质是( )
A、对角相等 B、对角线互相平分
C、对边平行且相等 D、对角线互相垂直
(2)如图,小强拿一张正方形的纸(图(1)),沿虚线对折
一次得图(2),再对折一次得图(3),然后用剪刀沿图(3)
中的虚线剪成两部分,再把所得的三角形的部分打开后的
形状一定是( )
A.一般的平行四边形 B、菱形 C、矩形 D、正方形
(1)
(2)
(3)
练一练4.
A
O
D
C
B
1、如图,已知正方形ABCD对角线交于点O,则∠BOC=________
2、如图,以定点A、B为其中两个顶点作为正方形,一共可以作( )
A、4个 B、3个 C、2个 D、1个
A
B
B
90°
练一练5.
1、在直角梯形ABCD中, ∠ C=∠D=90°,且∠ A:∠B=1:3,那么∠ A=_____________
2、在四边形ABCD中, 若∠ A:∠B :∠ C:∠D=2:2:1:3,则这个四边形是________________
A
B
C
D
3、在等腰梯形ABCD中,BD⊥DC,且∠C=60°,
若AD=5㎝,则梯形的腰长为____________㎝
4、在梯形ABCD中,AB//DC,将BC平移到ED的位置,
若∠A=55°,∠C=120°,则∠ADE等于____________
D
A
B
C
E
45°
65°
5
直角梯形
小测验 一、判断题:
(1)一组对边平行,另一组对边相等的四边形
是平行四边形。
(2)对角线相等的四边形是矩形。
(3)对角线互相垂直的四边形
是平行四边形。
(4)对角线相等且互相垂直的四边形
是正方形。
(5)连结矩形各边中点所得的四边形
是菱形。
动手动脑,小组探究。
1、将矩形纸片ABCD、沿对角线AC折叠,
使B点落在E处。则EF与DF有什么关系?
试证明你的结论。
A
B
C
D
E
F
答:EF与DF是相等关系
证明:矩形ABCD中:
∵ ∠B=∠E=∠D =90°
AB=AE=CD
又∵∠ AFE=∠CFD
∴ ΔAEF ≌ ΔCDF(AAS)
∴EF=DF
(全等三角形对应边相等)
二、 填空题:
1、 ABCD的对角线AC与BD交于O,若
S ABCD=12cm , S AOB=_______。
2、矩形对角线的交角为60°,一条对角线与
较短边的和为18cm, 则对角线长是______。
3、菱形的周长为16,高为2,则菱形相
邻的两角的 度数大小为______________。
4、菱形的对角线长为10和24,则周长
为_________。
5、正方形ABCD中,E为BC上一点,且EF⊥
BD于F, 那么 △EFB是_______三角形。
3cm
30°、150°
12cm
52
等腰直角
2.正方形ABCD的对角线相交于点O ,点 O是正方形
MNPO的一个顶点,如果两个正方形的边长相等,那么
正方形MNPO绕点 怎样转动,试猜想两个正方形重叠
部分的面积四边形OEAF与正方形的面积有什么关系?
并证明你的结论。
0
A
B
C
D
A
M
N
P
E
F
答:SOEAF =
SABCD
有谁证明?
A
B
C
D
O
E
F
证明:正方形ABCD中:
∵ ∠EDO=∠ FAO=45°
DO=AO
∠ 1=90°–∠ 3=∠ 2
∴ △ DOE≌ △ AOF(ASA)
又∵ S四边形EAFO=S△ OEA+S△ AOF
∴ S四边形EAFO= S△ OEA +S△DOE
= S△ AOD = SABCD
1
2
3
(
(
(
45°
45°
同学们努力呵!
只有多练才有提高!
