18.2.2 特殊的平行四边形——菱形的定义和性质 讲义2023-2024学年人教版数学八年级下册(无答案)
文档属性
| 名称 | 18.2.2 特殊的平行四边形——菱形的定义和性质 讲义2023-2024学年人教版数学八年级下册(无答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 139.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-04-17 00:00:00 | ||
图片预览

文档简介
课堂笔记以及课堂例题 人教版·八年级上册·第十八章 平行四边形
———————————————————————————
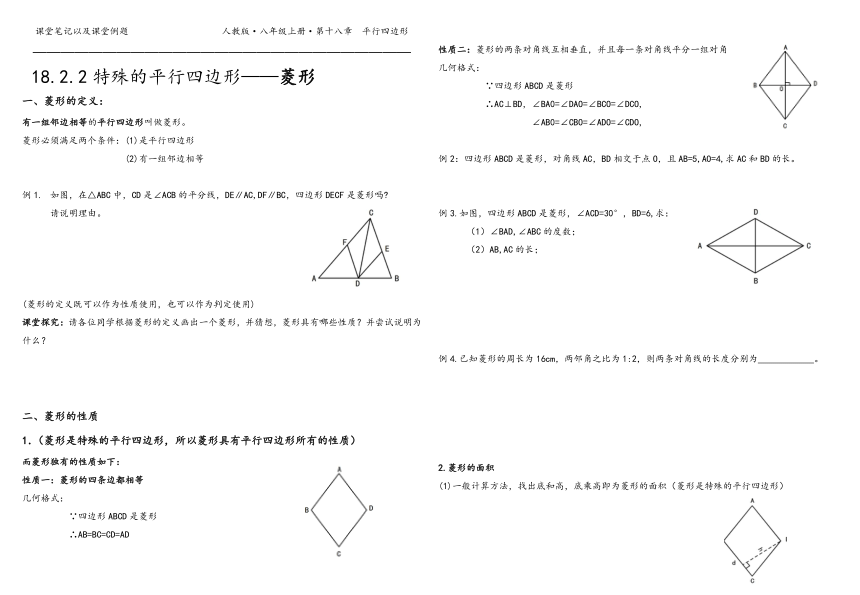
18.2.2特殊的平行四边形——菱形
一、菱形的定义:
有一组邻边相等的平行四边形叫做菱形。
菱形必须满足两个条件:(1)是平行四边形
(2)有一组邻边相等
如图,在△ABC中,CD是∠ACB的平分线,DE∥AC,DF∥BC,四边形DECF是菱形吗
请说明理由。
(菱形的定义既可以作为性质使用,也可以作为判定使用)
课堂探究:请各位同学根据菱形的定义画出一个菱形,并猜想,菱形具有哪些性质?并尝试说明为什么?
二、菱形的性质
1.(菱形是特殊的平行四边形,所以菱形具有平行四边形所有的性质)
而菱形独有的性质如下:
性质一:菱形的四条边都相等
几何格式:
∵四边形ABCD是菱形
∴AB=BC=CD=AD
性质二:菱形的两条对角线互相垂直,并且每一条对角线平分一组对角
几何格式:
∵四边形ABCD是菱形
∴AC⊥BD,∠BA0=∠DAO=∠BCO=∠DCO,
∠AB0=∠CBO=∠ADO=∠CDO,
例2:四边形ABCD是菱形,对角线AC,BD相交于点O,且AB=5,AO=4,求AC和BD的长。
例3.如图,四边形ABCD是菱形,∠ACD=30°,BD=6,求:
(1)∠BAD,∠ABC的度数;
(2)AB,AC的长;
例4.已知菱形的周长为16cm,两邻角之比为1:2,则两条对角线的长度分别为 。
2.菱形的面积
(1)一般计算方法,找出底和高,底乘高即为菱形的面积(菱形是特殊的平行四边形)
(2)特殊计算方法:(利用菱形的对角线垂直)
例3.如图,菱形花坛ABCD的边长为20m,∠ABC=60°,沿着菱形的对角线修剪了两条小路AC和BD,求两条小路的长和花坛的面积。
3.菱形对角线的作用:
菱形的两条对角线互相垂直,并且每一条对角线平分一组对角。
菱形是轴对称图形,对称轴就是对角线所在的直线。
菱形的两条对角线互相垂直,把菱形分成四个全等的直角三角形,进而可得菱形的边长的平方等于两条对角线长一半的平方和。
用来计算菱形的面积。
课堂练习:
1.菱形具有而普通平行四边形不具有的性质是( )
A. 两组对边分别平行 B. 四条边都相等 C. 对角线互相平分 D. 对角线互相垂直
E.一条对角线平分一组对角 D.两组对角分别相等
2.如图,在菱形ABCD中,∠D=150°,则∠CAB等于 。
3.如图,在平行四边形ABCD中,AB=4,BC=6,将线段AB水平向右平移a个单位长度得到线段EF,若四边形ECDF为菱形,则a的值为 。
4.如图,在菱形ABCD中,AC,BD为菱形的对角线,∠DBC=60°,BD=10,点E为BC的中点,则EF的长度为 。
5.若菱形两条对角线的长分别是4cm和12cm,则其面积是 cm 。
6.如图,四边形ABCD是边长为10cm的菱形,其中对角线BD的长为16cm,求:
(1)对角线AC的长。
(2)菱形ABCD的面积。
———————————————————————————
18.2.2特殊的平行四边形——菱形
一、菱形的定义:
有一组邻边相等的平行四边形叫做菱形。
菱形必须满足两个条件:(1)是平行四边形
(2)有一组邻边相等
如图,在△ABC中,CD是∠ACB的平分线,DE∥AC,DF∥BC,四边形DECF是菱形吗
请说明理由。
(菱形的定义既可以作为性质使用,也可以作为判定使用)
课堂探究:请各位同学根据菱形的定义画出一个菱形,并猜想,菱形具有哪些性质?并尝试说明为什么?
二、菱形的性质
1.(菱形是特殊的平行四边形,所以菱形具有平行四边形所有的性质)
而菱形独有的性质如下:
性质一:菱形的四条边都相等
几何格式:
∵四边形ABCD是菱形
∴AB=BC=CD=AD
性质二:菱形的两条对角线互相垂直,并且每一条对角线平分一组对角
几何格式:
∵四边形ABCD是菱形
∴AC⊥BD,∠BA0=∠DAO=∠BCO=∠DCO,
∠AB0=∠CBO=∠ADO=∠CDO,
例2:四边形ABCD是菱形,对角线AC,BD相交于点O,且AB=5,AO=4,求AC和BD的长。
例3.如图,四边形ABCD是菱形,∠ACD=30°,BD=6,求:
(1)∠BAD,∠ABC的度数;
(2)AB,AC的长;
例4.已知菱形的周长为16cm,两邻角之比为1:2,则两条对角线的长度分别为 。
2.菱形的面积
(1)一般计算方法,找出底和高,底乘高即为菱形的面积(菱形是特殊的平行四边形)
(2)特殊计算方法:(利用菱形的对角线垂直)
例3.如图,菱形花坛ABCD的边长为20m,∠ABC=60°,沿着菱形的对角线修剪了两条小路AC和BD,求两条小路的长和花坛的面积。
3.菱形对角线的作用:
菱形的两条对角线互相垂直,并且每一条对角线平分一组对角。
菱形是轴对称图形,对称轴就是对角线所在的直线。
菱形的两条对角线互相垂直,把菱形分成四个全等的直角三角形,进而可得菱形的边长的平方等于两条对角线长一半的平方和。
用来计算菱形的面积。
课堂练习:
1.菱形具有而普通平行四边形不具有的性质是( )
A. 两组对边分别平行 B. 四条边都相等 C. 对角线互相平分 D. 对角线互相垂直
E.一条对角线平分一组对角 D.两组对角分别相等
2.如图,在菱形ABCD中,∠D=150°,则∠CAB等于 。
3.如图,在平行四边形ABCD中,AB=4,BC=6,将线段AB水平向右平移a个单位长度得到线段EF,若四边形ECDF为菱形,则a的值为 。
4.如图,在菱形ABCD中,AC,BD为菱形的对角线,∠DBC=60°,BD=10,点E为BC的中点,则EF的长度为 。
5.若菱形两条对角线的长分别是4cm和12cm,则其面积是 cm 。
6.如图,四边形ABCD是边长为10cm的菱形,其中对角线BD的长为16cm,求:
(1)对角线AC的长。
(2)菱形ABCD的面积。
