人教版四年级数学上册 平行四边形复习课件(共33张PPT)
文档属性
| 名称 | 人教版四年级数学上册 平行四边形复习课件(共33张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-04-17 00:00:00 | ||
图片预览





文档简介
(共33张PPT)
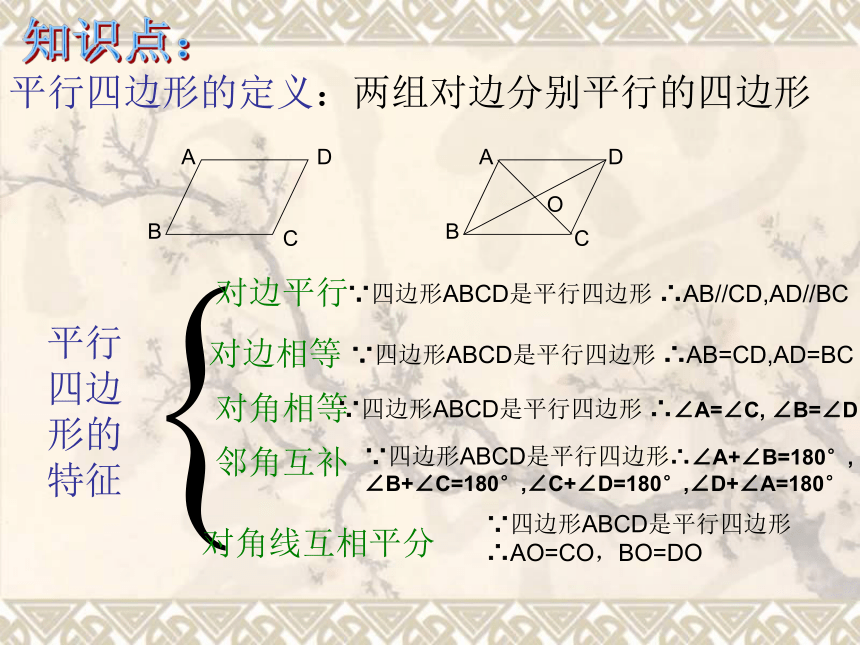
平行四边形复行四边形的定义:两组对边分别平行的四边形
平行四边形的特征
对边平行
对边相等
对角相等
邻角互补
对角线互相平分
∵四边形ABCD是平行四边形 ∴AB//CD,AD//BC
∵四边形ABCD是平行四边形 ∴AB=CD,AD=BC
∵四边形ABCD是平行四边形 ∴∠A=∠C, ∠B=∠D
∵四边形ABCD是平行四边形∴∠A+∠B=180°,
∠B+∠C=180°,∠C+∠D=180°,∠D+∠A=180°
∵四边形ABCD是平行四边形
∴AO=CO,BO=DO
A
B
C
D
A
B
C
D
O
知识点:
练一练
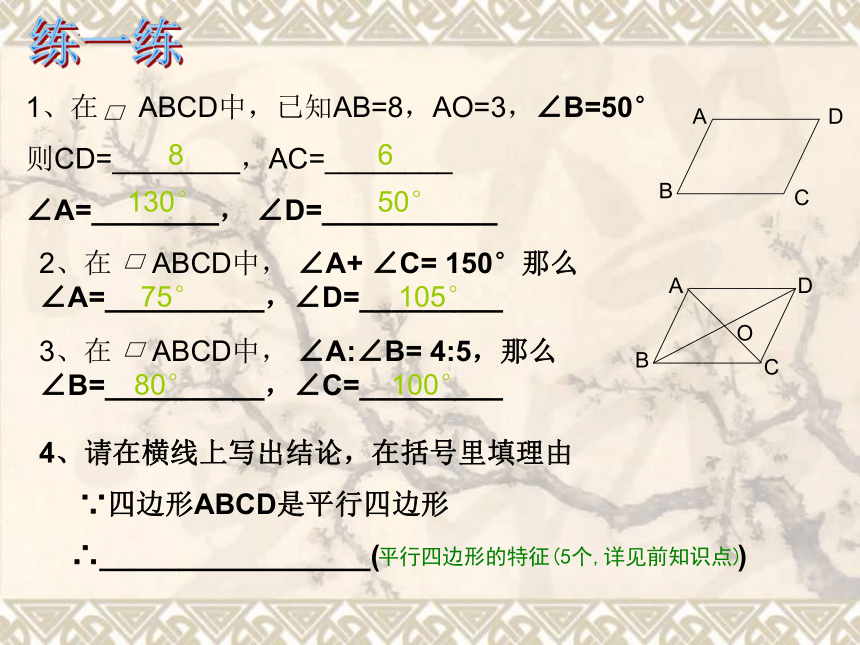
1、在 ABCD中,已知AB=8,AO=3,∠B=50°
则CD=________,AC=________
∠A=________, ∠D=___________
A
B
C
D
A
B
C
D
O
2、在 ABCD中, ∠A+ ∠C= 150°那么
∠A=__________,∠D=_________
3、在 ABCD中, ∠A:∠B= 4:5,那么
∠B=__________,∠C=_________
4、请在横线上写出结论,在括号里填理由
∵四边形ABCD是平行四边形
∴_________________( )
8
130°
6
75°
50°
105°
80°
100°
平行四边形的特征(5个,详见前知识点)
矩形
矩形的定义:有一个角是直角的平行四边形。
矩形的特征
具有平行四边形的一切特征
四个角都是直角
对角线相等且平分
A
C
D
O
B
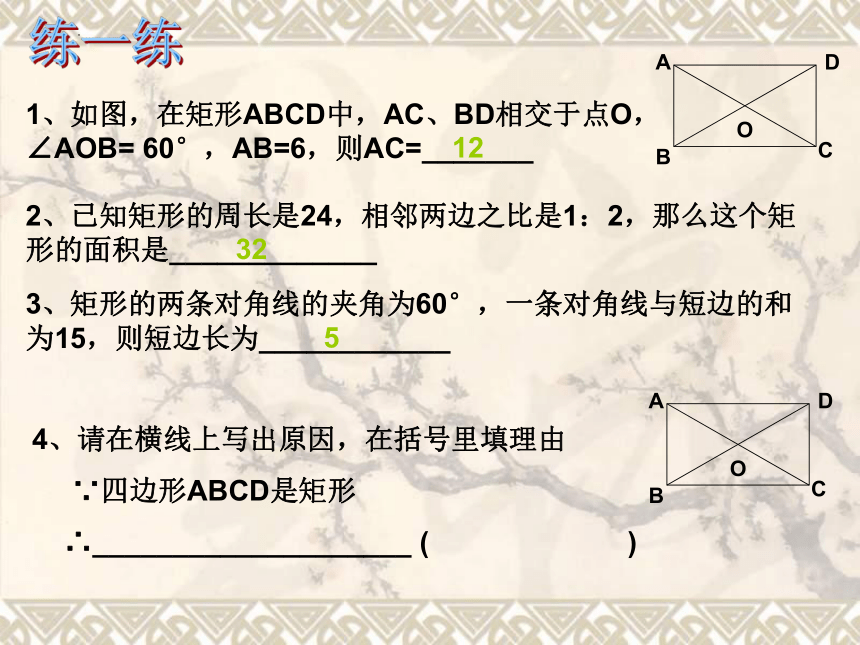
1、如图,在矩形ABCD中,AC、BD相交于点O, ∠AOB= 60°,AB=6,则AC=_______
练一练
2、已知矩形的周长是24,相邻两边之比是1:2,那么这个矩形的面积是_____________
3、矩形的两条对角线的夹角为60°,一条对角线与短边的和为15,则短边长为____________
A
C
D
O
B
4、请在横线上写出原因,在括号里填理由
∵四边形ABCD是矩形
∴____________________ ( )
12
32
5
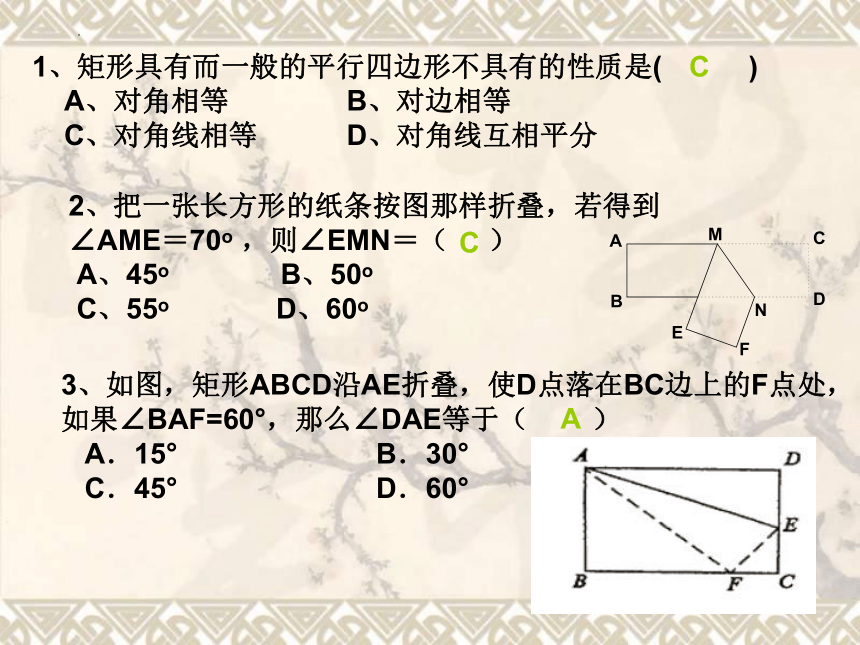
1、矩形具有而一般的平行四边形不具有的性质是( )
A、对角相等 B、对边相等
C、对角线相等 D、对角线互相平分
2、把一张长方形的纸条按图那样折叠,若得到
∠AME=70o ,则∠EMN=( )
A、45o B、50o
C、55o D、60o
3、如图,矩形ABCD沿AE折叠,使D点落在BC边上的F点处,
如果∠BAF=60°,那么∠DAE等于( )
A.15° B.30°
C.45° D.60°
A
C
C
菱形
菱形的定义:有一组邻边相等的平行四边形。
菱形的特征
具有平行四边形的一切特征
四条边相等
对角线互相垂直平分
对角线分别平分两组对角
A
B
C
D
O
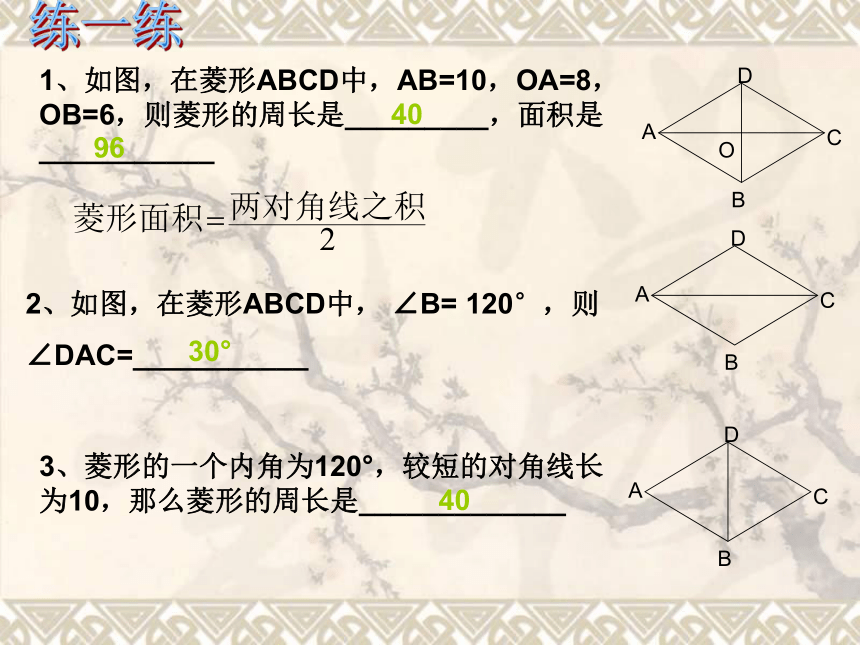
1、如图,在菱形ABCD中,AB=10,OA=8,OB=6,则菱形的周长是_________,面积是___________
2、如图,在菱形ABCD中, ∠B= 120°,则
∠DAC=___________
A
B
C
D
A
B
C
D
3、菱形的一个内角为120°,较短的对角线长为10,那么菱形的周长是_____________
96
40
30°
40
练一练
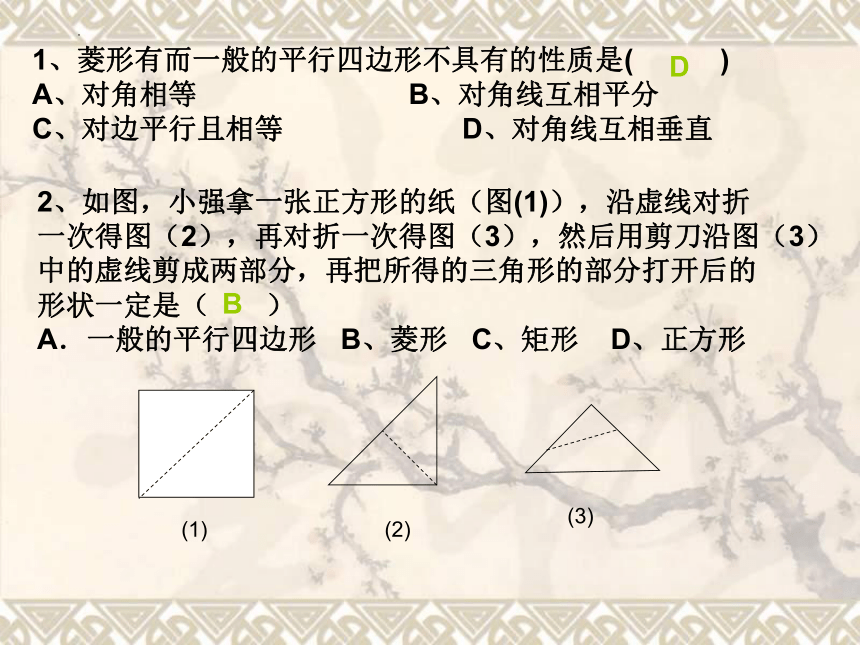
1、菱形有而一般的平行四边形不具有的性质是( )
A、对角相等 B、对角线互相平分
C、对边平行且相等 D、对角线互相垂直
2、如图,小强拿一张正方形的纸(图(1)),沿虚线对折
一次得图(2),再对折一次得图(3),然后用剪刀沿图(3)
中的虚线剪成两部分,再把所得的三角形的部分打开后的
形状一定是( )
A.一般的平行四边形 B、菱形 C、矩形 D、正方形
(1)
(2)
(3)
D
B
正方形
正方形的定义:有一组邻边相等且有一个角是直角的平行四边形。
正方形的特征
四条边相等
对角线互相垂直平分且相等
对角线分别平分两组对角
对边平行
四个角都是直角
练一练
A
O
D
C
B
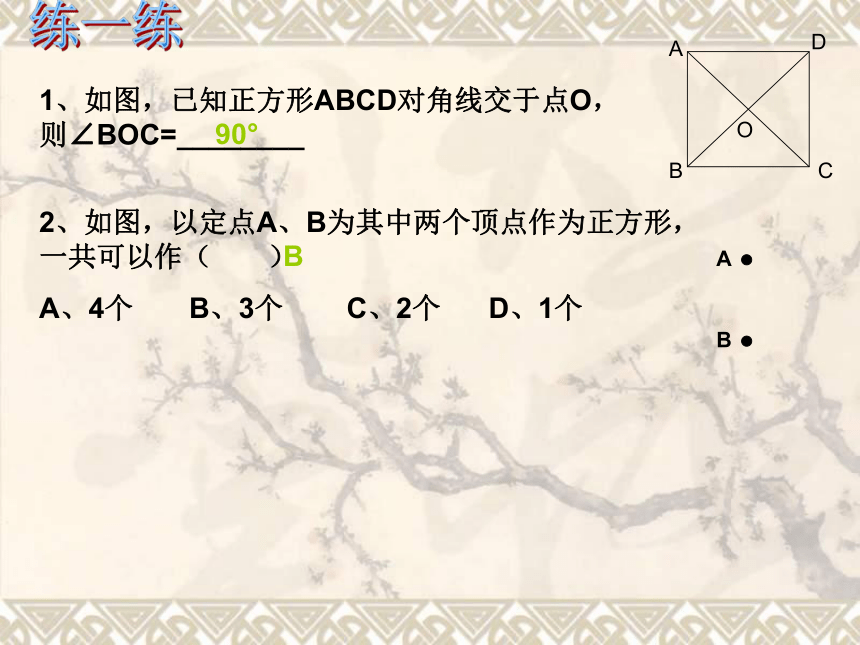
1、如图,已知正方形ABCD对角线交于点O,则∠BOC=________
2、如图,以定点A、B为其中两个顶点作为正方形,一共可以作( )
A、4个 B、3个 C、2个 D、1个
A
B
B
90°
梯形
梯形的定义:一组对边平行而另一组对边不平行的四边形
等腰梯形的特征
两腰相等
对角线相等
两底平行
同一底上的两个内角相等
练一练
1、在直角梯形ABCD中, ∠ C=∠D=90°,且∠ A:∠B=1:3,那么∠ A=_____________
2、在四边形ABCD中, 若∠ A:∠B :∠ C:∠D=2:2:1:3,则这个四边形是________________
A
B
C
D
3、在等腰梯形ABCD中,BD⊥DC,且∠C=60°,
若AD=5㎝,则梯形的腰长为____________㎝
4、在梯形ABCD中,AB//DC,将BC平移到ED的位置,
若∠A=55°,∠C=120°,则∠ADE等于____________
D
A
B
C
E
45°
65°
5
直角梯形
几种平行四边形的特征比较
图形 元素 边 角 对角线
对边平行且相等
对边平行且相等
对边平行,四条边都
相等
对边平行,四条边
相等
对角相等,邻角互补
四个角都为直角
对角相等,邻角互补
四个角都为直角
对角线互相平分
对角线相等且互相
平分
对角线互相垂直平
分,每条对角线平分
对角
对角线互相垂直平
分且相等,每条对角线平分对角
几种特殊四边形的特征
平行
四边形
矩 形
菱 形
正方形
等腰梯形
边
对边平行
且相等
对边平行
且相等
对边平行,四
条边都相等
对边平行,
四条边
都相等
两底平行,
两腰相等
角
对角相等
四个角
都是直角
对角相等
四个角
都是直角
同一底上的
两个角相等
对 角 线
两条对角线互相平分
两条对角线互相平分且相等
两条对角线互相垂直平分,
每条对角线平分一组对角
两条对角线互相垂直平分
且相等,每条对角线平分
一组对角
两条对角线相等
对称性
中心对称
轴对称(2条)
中心对称
轴对称(2条)
中心对称
轴对称(4条)
中心对称
轴对称(1条)
其他重要定理
1. 四边形的内角和等于
360°.
2. n 边形的内角和等于
( n – 2 )
.
180°.
3. 任意多边形的外角和等于
360°.
4. 关于中心对称的两个图形的性质:
(1)是全等形;
(2)对称点的连线都经过对称中心并且被对称中心平分。
巩固练习
(一)判断题:
1.平行四边形的对角线相等; ( )
2.矩形的四个角都相等; ( )
3.菱形的对角线互相垂直平分; ( )
4.有一个角是直角且邻边相等的平行四边形是正方形; ( )
5.一组对边平行的四边形是梯形; ( )
6.有两个角相等的梯形是等腰梯形; ( )
7.一组对边平行且相等的四边形是平行四边形; ( )
8.对角线相等的四边形是矩形; ( )
9.在梯形中上面的底叫做上底,下面的底叫做下底;( )
10.正方形既是轴对称图形又是中心对称图形。( )
(二)选择题:
D
2.正方形具有而菱形不一定具有的性质是( )。
(A)对角线互相平分。 (B)对角线相等。
(C)对角线平分一组对角。 (D)对角线互相垂直。
B
3.顺次连结四边形各边中点所得到的四边形一定是( )
(A)矩形。 (B)正方形。(C ) 菱形。(D)平行四边形
D
4.内角和等于外角和的多边形是( )
(A) 三角形。(B)四边形。(C )五边形。(D)六边形。
B
5.下列性质中,平行四边形不一定具备的是( )
(A)对角相等。(B)邻角互补。(C )对角互补。(D)内角和是360°。
C
(A)一组对边平行,另一组对边也平行;(B)一组对角相等,另一组对角也相等;
1.下面判定四边形是平行四边形的方法中,错误的是( )。
(C )一组对边平行,一组对角相等; (D)一组对边平行,另一组对边相等
6.能够判定一个四边形是平行四边形的条件是( )
(A)一组对角相等。 (B)两条对角线互相平分。
(C )两条对角线互相垂直。 (D)一对邻角的和为180°。
B
7.下列图形中,既是轴对称图形又是中心对称图形的是( )
(A)等边三角形。(B)平行四边形。(C )菱形。(D)等腰梯形。
C
D
9.不能判定四边形ABCD是平行四边形的条件是( )
//
(A) AB =CD, AD =BC。(B) BC AD。
(C ) AB//DC, AD//BC。 (D) AB =CD,AD//BC。
D
8.下列图形中,既是轴对称图形又是中心对称图形的是( )
(A)
(B)
(C )
(D)
复习题 A组
1. 观察下列挂件的图形,将它们分割成一个个你所熟悉的图形,分别指出它们的名称.
答案不唯一,看你如何分割.
2. 如图,在?ABCD中,过点P画线段EF、GH分别平行于AB、BC,试找出图中的平行四边形,与你的同伴比一比,看看谁找出的多.
解:共有9个平行四边形AGPE,GBFP,EPHD,PFCH,AGHD,GBCH,ABFE,EFCD,ABCD.
3. 如图,在?ABCD中,∠BAC=68°, ∠ACB=36°,求∠D和∠BCD的度数.
解:在?ABCD中,
∠D=∠B= 180°- ∠BAC - ∠ACB
= 180°- 68°- 36°= 76°;
∠BCD=∠BAD= 180°-∠B
= 180°- 76°= 104°.
4. 如图,在矩形ABCD中,相邻两边AB、BC分别长15cm和25cm,内角∠BAD的角平分线与边BC交于点E.试求BE与CE的长度.
解:∵内角∠BAD的角平分线与边BC交于点E
∴∠BAE= ∠BAD= ×90°= 45°
∵∠BEA= 90°- ∠BAE= 90°- 45°= 45°
∴∠BAE= ∠BEA ∴BE=BA= 15cm;
∴CE=BC-BE=25-15=10cm.
2
1
2
1
5. 已知正方形ABCD的一条对角线AC长为4cm,求它的边长和面积.
解:设正方形ABCD的边长为X,则
+
∴X=√8 cm ;
∴正方形ABCD的面积= = 8(平方厘米).
X2
X2
=42
X2
B组
6. 如图,在?ABCD中,AB=BE,连结AE,并延长与DC的延长线交于点F,∠F=62°,求这个平行四边形各内角的度数.
解:∵AB//DF,∴∠BAE= ∠F=62°,
∵ AB=BE,∴∠AEB= ∠BAE =62°
∴∠B=∠D= 180°- ∠AEB- ∠BAE
= 180°- 62°- 62°= 56°;
∵AD//BC, ∴∠EAD=∠AEB= 62°
∴∠BAD=∠BCD=∠BAE+∠EAD
= 62°+ 62°= 124°.
7. 如图,在梯形ABCD中,AD∥BC,AD=AB, BC=BD,∠A=120°,求梯形其他各内角的度数.
解:∵ AD∥BC ∴∠ABC+∠A= 180°
∴∠ABC= 180°-∠A
= 180°- 120°= 60°;
∵ AD=AB
∴∠ABD=∠ADB = (180°-∠A)
= (180°- 120°)= 30°
∴∠DBC=∠ABC-∠ABD
= 60°- 30°= 30°
∵ BC=BD
∴∠C=∠BDC = (180°-∠DBC)
= (180°- 30°)= 75°;
∴∠ADC= ∠ADB+ ∠BDC
= 30°+ 75°= 105°.
2
1
2
1
2
1
2
1
8. 如图,在正三角形ABC中,D、E、F分别为三边BC、CA、AB的中点,看一看,数一数,在整个图形中,有多少个三角形 多少个平行四边形 多少个菱形 多少个等腰梯形?(本题只要求观察,说出你数得的个数)
解:①有5个三角形(ABC,AFE,FBD,FDE,EDC)
②有3个平行四边形(AFDE,FBDE,FDCE)
③有3个菱形(AFDE,FBDE,FDCE)
④有3个等腰梯形(DEAB,DFAC,EFBC)
9. 如图,在等腰梯形ABCD中,AB=DC, ∠B=60°, DE∥AB.试说明
(1) DE=DC;
(2) △DEC是一个等边三角形.
解(1)∵在等腰梯形ABCD中,AB=DC, ∴∠C= ∠B=60°
∵ DE∥AB, ∴∠DEC= ∠B=60°,
∴∠C=∠DEC= 60°, ∴ DE=DC(等角对等边)
(2) ∵ ∠C=∠DEC= 60°,
∴∠CDE= 180°- 60°- 60°= 60°,
∴ ∠C=∠DEC= ∠CDE = 60°,
∴ △DEC是一个等边三角形.
10. 梯形ABCD中,AD∥BC,且∠A=2∠B=4∠C,求∠D的度数.
解:∵ AD∥BC,
∴∠A+∠B= 180°,∠C+∠D= 180°, ∴∠C= 180°-∠D
∵ ∠A=2∠B=4∠C,
∴ ∠A=4∠C=4(180°-∠D)
∠B=2∠C=2(180°-∠D)
∴ ∠A+∠B=4(180°-∠D)+ 2(180°-∠D)
=6(180°-∠D)= 180°
∴ 180°-∠D= 180÷6 = 30°
∴ ∠D=150°.
C组
11. 如图,D是等腰三角形ABC的底边BC上的一点,E、F分别在AC、AB上,且DE∥AB, DF∥AC.试问DE、DF与AB之间有什么关系吗 请说明理由.
解:DE+DF=AB
∵ DE∥AB, DF∥AC.
∴四边形AFDE是平行四边形
∴DE=FA
∵△ABC是等腰三角形
∴∠B=∠C
∵ DF∥AC
∴∠FDB=∠C
∴∠B=∠FDB
∴DF=BF
∴DE+DF=FA+BF=AB.
12. 如图,正方形ABCD的对角线交于点O,点O又是另一个正方形A′B′C′O的一个顶点.如果两个正方形的边长相等,那么正方形A′B′C′O绕点O无论怎样旋转,两个正方形重叠部分的面积,总等于一个正方形面积的四分之一.想一想,这是为什么?
13. 请你用不同的方法将一个矩形分成面积相等的两部分.
(1) 观察一下所分成的两部分图形之间的位置关系;
(2) 如果你用的是直线,那么这样的直线有多少条 它们之间又有什么联系呢
(3) 若将矩形分成面积相等的四部分,你又能发现什么
所分成的两部分图形关于对角线的交点成中心对称
如果用直线分割,那么这样的直线有无数条,它们都经过对角线的交点.
如果用直线分割,其中不少方法所得的面积相等的四部分中有两部分分别存在对称关系,但不是全部方法都能.
同学们再见!
平行四边形复行四边形的定义:两组对边分别平行的四边形
平行四边形的特征
对边平行
对边相等
对角相等
邻角互补
对角线互相平分
∵四边形ABCD是平行四边形 ∴AB//CD,AD//BC
∵四边形ABCD是平行四边形 ∴AB=CD,AD=BC
∵四边形ABCD是平行四边形 ∴∠A=∠C, ∠B=∠D
∵四边形ABCD是平行四边形∴∠A+∠B=180°,
∠B+∠C=180°,∠C+∠D=180°,∠D+∠A=180°
∵四边形ABCD是平行四边形
∴AO=CO,BO=DO
A
B
C
D
A
B
C
D
O
知识点:
练一练
1、在 ABCD中,已知AB=8,AO=3,∠B=50°
则CD=________,AC=________
∠A=________, ∠D=___________
A
B
C
D
A
B
C
D
O
2、在 ABCD中, ∠A+ ∠C= 150°那么
∠A=__________,∠D=_________
3、在 ABCD中, ∠A:∠B= 4:5,那么
∠B=__________,∠C=_________
4、请在横线上写出结论,在括号里填理由
∵四边形ABCD是平行四边形
∴_________________( )
8
130°
6
75°
50°
105°
80°
100°
平行四边形的特征(5个,详见前知识点)
矩形
矩形的定义:有一个角是直角的平行四边形。
矩形的特征
具有平行四边形的一切特征
四个角都是直角
对角线相等且平分
A
C
D
O
B
1、如图,在矩形ABCD中,AC、BD相交于点O, ∠AOB= 60°,AB=6,则AC=_______
练一练
2、已知矩形的周长是24,相邻两边之比是1:2,那么这个矩形的面积是_____________
3、矩形的两条对角线的夹角为60°,一条对角线与短边的和为15,则短边长为____________
A
C
D
O
B
4、请在横线上写出原因,在括号里填理由
∵四边形ABCD是矩形
∴____________________ ( )
12
32
5
1、矩形具有而一般的平行四边形不具有的性质是( )
A、对角相等 B、对边相等
C、对角线相等 D、对角线互相平分
2、把一张长方形的纸条按图那样折叠,若得到
∠AME=70o ,则∠EMN=( )
A、45o B、50o
C、55o D、60o
3、如图,矩形ABCD沿AE折叠,使D点落在BC边上的F点处,
如果∠BAF=60°,那么∠DAE等于( )
A.15° B.30°
C.45° D.60°
A
C
C
菱形
菱形的定义:有一组邻边相等的平行四边形。
菱形的特征
具有平行四边形的一切特征
四条边相等
对角线互相垂直平分
对角线分别平分两组对角
A
B
C
D
O
1、如图,在菱形ABCD中,AB=10,OA=8,OB=6,则菱形的周长是_________,面积是___________
2、如图,在菱形ABCD中, ∠B= 120°,则
∠DAC=___________
A
B
C
D
A
B
C
D
3、菱形的一个内角为120°,较短的对角线长为10,那么菱形的周长是_____________
96
40
30°
40
练一练
1、菱形有而一般的平行四边形不具有的性质是( )
A、对角相等 B、对角线互相平分
C、对边平行且相等 D、对角线互相垂直
2、如图,小强拿一张正方形的纸(图(1)),沿虚线对折
一次得图(2),再对折一次得图(3),然后用剪刀沿图(3)
中的虚线剪成两部分,再把所得的三角形的部分打开后的
形状一定是( )
A.一般的平行四边形 B、菱形 C、矩形 D、正方形
(1)
(2)
(3)
D
B
正方形
正方形的定义:有一组邻边相等且有一个角是直角的平行四边形。
正方形的特征
四条边相等
对角线互相垂直平分且相等
对角线分别平分两组对角
对边平行
四个角都是直角
练一练
A
O
D
C
B
1、如图,已知正方形ABCD对角线交于点O,则∠BOC=________
2、如图,以定点A、B为其中两个顶点作为正方形,一共可以作( )
A、4个 B、3个 C、2个 D、1个
A
B
B
90°
梯形
梯形的定义:一组对边平行而另一组对边不平行的四边形
等腰梯形的特征
两腰相等
对角线相等
两底平行
同一底上的两个内角相等
练一练
1、在直角梯形ABCD中, ∠ C=∠D=90°,且∠ A:∠B=1:3,那么∠ A=_____________
2、在四边形ABCD中, 若∠ A:∠B :∠ C:∠D=2:2:1:3,则这个四边形是________________
A
B
C
D
3、在等腰梯形ABCD中,BD⊥DC,且∠C=60°,
若AD=5㎝,则梯形的腰长为____________㎝
4、在梯形ABCD中,AB//DC,将BC平移到ED的位置,
若∠A=55°,∠C=120°,则∠ADE等于____________
D
A
B
C
E
45°
65°
5
直角梯形
几种平行四边形的特征比较
图形 元素 边 角 对角线
对边平行且相等
对边平行且相等
对边平行,四条边都
相等
对边平行,四条边
相等
对角相等,邻角互补
四个角都为直角
对角相等,邻角互补
四个角都为直角
对角线互相平分
对角线相等且互相
平分
对角线互相垂直平
分,每条对角线平分
对角
对角线互相垂直平
分且相等,每条对角线平分对角
几种特殊四边形的特征
平行
四边形
矩 形
菱 形
正方形
等腰梯形
边
对边平行
且相等
对边平行
且相等
对边平行,四
条边都相等
对边平行,
四条边
都相等
两底平行,
两腰相等
角
对角相等
四个角
都是直角
对角相等
四个角
都是直角
同一底上的
两个角相等
对 角 线
两条对角线互相平分
两条对角线互相平分且相等
两条对角线互相垂直平分,
每条对角线平分一组对角
两条对角线互相垂直平分
且相等,每条对角线平分
一组对角
两条对角线相等
对称性
中心对称
轴对称(2条)
中心对称
轴对称(2条)
中心对称
轴对称(4条)
中心对称
轴对称(1条)
其他重要定理
1. 四边形的内角和等于
360°.
2. n 边形的内角和等于
( n – 2 )
.
180°.
3. 任意多边形的外角和等于
360°.
4. 关于中心对称的两个图形的性质:
(1)是全等形;
(2)对称点的连线都经过对称中心并且被对称中心平分。
巩固练习
(一)判断题:
1.平行四边形的对角线相等; ( )
2.矩形的四个角都相等; ( )
3.菱形的对角线互相垂直平分; ( )
4.有一个角是直角且邻边相等的平行四边形是正方形; ( )
5.一组对边平行的四边形是梯形; ( )
6.有两个角相等的梯形是等腰梯形; ( )
7.一组对边平行且相等的四边形是平行四边形; ( )
8.对角线相等的四边形是矩形; ( )
9.在梯形中上面的底叫做上底,下面的底叫做下底;( )
10.正方形既是轴对称图形又是中心对称图形。( )
(二)选择题:
D
2.正方形具有而菱形不一定具有的性质是( )。
(A)对角线互相平分。 (B)对角线相等。
(C)对角线平分一组对角。 (D)对角线互相垂直。
B
3.顺次连结四边形各边中点所得到的四边形一定是( )
(A)矩形。 (B)正方形。(C ) 菱形。(D)平行四边形
D
4.内角和等于外角和的多边形是( )
(A) 三角形。(B)四边形。(C )五边形。(D)六边形。
B
5.下列性质中,平行四边形不一定具备的是( )
(A)对角相等。(B)邻角互补。(C )对角互补。(D)内角和是360°。
C
(A)一组对边平行,另一组对边也平行;(B)一组对角相等,另一组对角也相等;
1.下面判定四边形是平行四边形的方法中,错误的是( )。
(C )一组对边平行,一组对角相等; (D)一组对边平行,另一组对边相等
6.能够判定一个四边形是平行四边形的条件是( )
(A)一组对角相等。 (B)两条对角线互相平分。
(C )两条对角线互相垂直。 (D)一对邻角的和为180°。
B
7.下列图形中,既是轴对称图形又是中心对称图形的是( )
(A)等边三角形。(B)平行四边形。(C )菱形。(D)等腰梯形。
C
D
9.不能判定四边形ABCD是平行四边形的条件是( )
//
(A) AB =CD, AD =BC。(B) BC AD。
(C ) AB//DC, AD//BC。 (D) AB =CD,AD//BC。
D
8.下列图形中,既是轴对称图形又是中心对称图形的是( )
(A)
(B)
(C )
(D)
复习题 A组
1. 观察下列挂件的图形,将它们分割成一个个你所熟悉的图形,分别指出它们的名称.
答案不唯一,看你如何分割.
2. 如图,在?ABCD中,过点P画线段EF、GH分别平行于AB、BC,试找出图中的平行四边形,与你的同伴比一比,看看谁找出的多.
解:共有9个平行四边形AGPE,GBFP,EPHD,PFCH,AGHD,GBCH,ABFE,EFCD,ABCD.
3. 如图,在?ABCD中,∠BAC=68°, ∠ACB=36°,求∠D和∠BCD的度数.
解:在?ABCD中,
∠D=∠B= 180°- ∠BAC - ∠ACB
= 180°- 68°- 36°= 76°;
∠BCD=∠BAD= 180°-∠B
= 180°- 76°= 104°.
4. 如图,在矩形ABCD中,相邻两边AB、BC分别长15cm和25cm,内角∠BAD的角平分线与边BC交于点E.试求BE与CE的长度.
解:∵内角∠BAD的角平分线与边BC交于点E
∴∠BAE= ∠BAD= ×90°= 45°
∵∠BEA= 90°- ∠BAE= 90°- 45°= 45°
∴∠BAE= ∠BEA ∴BE=BA= 15cm;
∴CE=BC-BE=25-15=10cm.
2
1
2
1
5. 已知正方形ABCD的一条对角线AC长为4cm,求它的边长和面积.
解:设正方形ABCD的边长为X,则
+
∴X=√8 cm ;
∴正方形ABCD的面积= = 8(平方厘米).
X2
X2
=42
X2
B组
6. 如图,在?ABCD中,AB=BE,连结AE,并延长与DC的延长线交于点F,∠F=62°,求这个平行四边形各内角的度数.
解:∵AB//DF,∴∠BAE= ∠F=62°,
∵ AB=BE,∴∠AEB= ∠BAE =62°
∴∠B=∠D= 180°- ∠AEB- ∠BAE
= 180°- 62°- 62°= 56°;
∵AD//BC, ∴∠EAD=∠AEB= 62°
∴∠BAD=∠BCD=∠BAE+∠EAD
= 62°+ 62°= 124°.
7. 如图,在梯形ABCD中,AD∥BC,AD=AB, BC=BD,∠A=120°,求梯形其他各内角的度数.
解:∵ AD∥BC ∴∠ABC+∠A= 180°
∴∠ABC= 180°-∠A
= 180°- 120°= 60°;
∵ AD=AB
∴∠ABD=∠ADB = (180°-∠A)
= (180°- 120°)= 30°
∴∠DBC=∠ABC-∠ABD
= 60°- 30°= 30°
∵ BC=BD
∴∠C=∠BDC = (180°-∠DBC)
= (180°- 30°)= 75°;
∴∠ADC= ∠ADB+ ∠BDC
= 30°+ 75°= 105°.
2
1
2
1
2
1
2
1
8. 如图,在正三角形ABC中,D、E、F分别为三边BC、CA、AB的中点,看一看,数一数,在整个图形中,有多少个三角形 多少个平行四边形 多少个菱形 多少个等腰梯形?(本题只要求观察,说出你数得的个数)
解:①有5个三角形(ABC,AFE,FBD,FDE,EDC)
②有3个平行四边形(AFDE,FBDE,FDCE)
③有3个菱形(AFDE,FBDE,FDCE)
④有3个等腰梯形(DEAB,DFAC,EFBC)
9. 如图,在等腰梯形ABCD中,AB=DC, ∠B=60°, DE∥AB.试说明
(1) DE=DC;
(2) △DEC是一个等边三角形.
解(1)∵在等腰梯形ABCD中,AB=DC, ∴∠C= ∠B=60°
∵ DE∥AB, ∴∠DEC= ∠B=60°,
∴∠C=∠DEC= 60°, ∴ DE=DC(等角对等边)
(2) ∵ ∠C=∠DEC= 60°,
∴∠CDE= 180°- 60°- 60°= 60°,
∴ ∠C=∠DEC= ∠CDE = 60°,
∴ △DEC是一个等边三角形.
10. 梯形ABCD中,AD∥BC,且∠A=2∠B=4∠C,求∠D的度数.
解:∵ AD∥BC,
∴∠A+∠B= 180°,∠C+∠D= 180°, ∴∠C= 180°-∠D
∵ ∠A=2∠B=4∠C,
∴ ∠A=4∠C=4(180°-∠D)
∠B=2∠C=2(180°-∠D)
∴ ∠A+∠B=4(180°-∠D)+ 2(180°-∠D)
=6(180°-∠D)= 180°
∴ 180°-∠D= 180÷6 = 30°
∴ ∠D=150°.
C组
11. 如图,D是等腰三角形ABC的底边BC上的一点,E、F分别在AC、AB上,且DE∥AB, DF∥AC.试问DE、DF与AB之间有什么关系吗 请说明理由.
解:DE+DF=AB
∵ DE∥AB, DF∥AC.
∴四边形AFDE是平行四边形
∴DE=FA
∵△ABC是等腰三角形
∴∠B=∠C
∵ DF∥AC
∴∠FDB=∠C
∴∠B=∠FDB
∴DF=BF
∴DE+DF=FA+BF=AB.
12. 如图,正方形ABCD的对角线交于点O,点O又是另一个正方形A′B′C′O的一个顶点.如果两个正方形的边长相等,那么正方形A′B′C′O绕点O无论怎样旋转,两个正方形重叠部分的面积,总等于一个正方形面积的四分之一.想一想,这是为什么?
13. 请你用不同的方法将一个矩形分成面积相等的两部分.
(1) 观察一下所分成的两部分图形之间的位置关系;
(2) 如果你用的是直线,那么这样的直线有多少条 它们之间又有什么联系呢
(3) 若将矩形分成面积相等的四部分,你又能发现什么
所分成的两部分图形关于对角线的交点成中心对称
如果用直线分割,那么这样的直线有无数条,它们都经过对角线的交点.
如果用直线分割,其中不少方法所得的面积相等的四部分中有两部分分别存在对称关系,但不是全部方法都能.
同学们再见!
