安徽省亳州市谯城区古城中心中学人教版九年级数学上册(25-3 用频率估计概率》同步测试
文档属性
| 名称 | 安徽省亳州市谯城区古城中心中学人教版九年级数学上册(25-3 用频率估计概率》同步测试 |  | |
| 格式 | zip | ||
| 文件大小 | 591.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2015-10-24 20:54:20 | ||
图片预览

文档简介
自我小测
复习巩固
1.已知抛一枚均匀硬币正面朝上的概率为,则下列说法中,错误的是( )
A.连续抛一枚均匀硬币2次必有1次正面朝上
B.连续抛一枚均匀硬币10次都可能正面朝上
C.大量反复抛一枚均匀硬币,平均每100次出现正面朝上50次
D.通过抛一枚均匀硬币确定谁先发球的比赛规则是公平的
2.在一盒子里有红、黄、蓝球共100个, ( http: / / www.21cnjy.com )小明总结多次摸球的规律:红球、黄球、蓝球的概率依次是35%,25%,40%,则估计红、黄、蓝球的个数分别是( )
A.35,25,40 B.40,25,35
C.35,40,25 D.40,35,25
3.在一次质检抽测中,随机抽取某摊位20袋食盐,测得各袋的质量分别为(单位:g):
492 496 494 495 498 497 501 502
504 496 497 503 506 508 507 492
496 500 501 499
根据以上抽测结果,任买1袋该摊位的食盐,质量在497.5 g~501.5 g之间的概率为( )
A. B.
C. D.
4.某射手在同一条件下,射击200次,击中靶心100次,射击400次,击中靶心121次,射击800次,击中靶心240次,则该射手射击一次击中靶心的概率约为__________.
5.在“抛掷正六面体”的试验中,如果正六面体的六个面上分别标有数字1,2,3,4,5和6,随着试验的次数增多,出现数字“1”的频率的变化趋势是__________.
6.小颖和小红两位同学在学习“概率”时,做了抛掷骰子(质地均匀的正方体)试验,她们共做了60次,试验的结果如下:
朝上的点数 1 2 3 4 5 6
出现的次数 7 9 6 8 20 10
(1)计算“3点朝上”的频率和“5点朝上”的频率.
(2)小颖说:“根据试验,一次试验中出现5 ( http: / / www.21cnjy.com )点朝上的概率最大”;小红说:“如果抛掷600次,那么出现6点朝上的次数正好是100次.”小颖和小红的说法正确吗?为什么?
(3)小颖和小红各抛掷一枚骰子,用列表或画树状图的方法求出两个骰子朝上的点数之和为3的倍数的概率.
能力提升
7.一个不透明的盒子里有n个除颜色外其他完全相同的小球,其中有6个黄球.每次摸球前先将盒子里的球摇匀,任意摸出1个球记下颜色后再放回盒子,通过大量重复摸球试验后发现,摸到黄球的频率稳定在30%,那么可以推算出n大约是( )
A.6 B.10 C.18 D.20
8.生物工作者为了估计一片山林中雀鸟的数量,设计了如下方案:先捕捉100只雀鸟,给它们做上标记后放回山林,一段时间后,再从中随机捕获500只,其中有标记的雀鸟有5只.请你帮助工作人员估计这片山林中雀鸟的数量,约有______只.
9.在一次统计中,调查了英文文献中字母E的使用率,在几段英文文献中字母E的使用数据如下表所示.
(1)请你将下表补充完整.
文献中字母的个数 982 11 237 534 406 33 569 792 108 274 953 2 195 680 075
文献中字母E的个数 121 903 52 381 3 411 079 10 719 220 220 665 847
文献中字母E的使用率 0.123
(2)通过计算表中数据可以发现,字母E的使 ( http: / / www.21cnjy.com )用率在__________左右摆动,并且随着统计数据的增加,这种规律愈加明显,所以估计字母E在英文文献中的使用概率是__________.
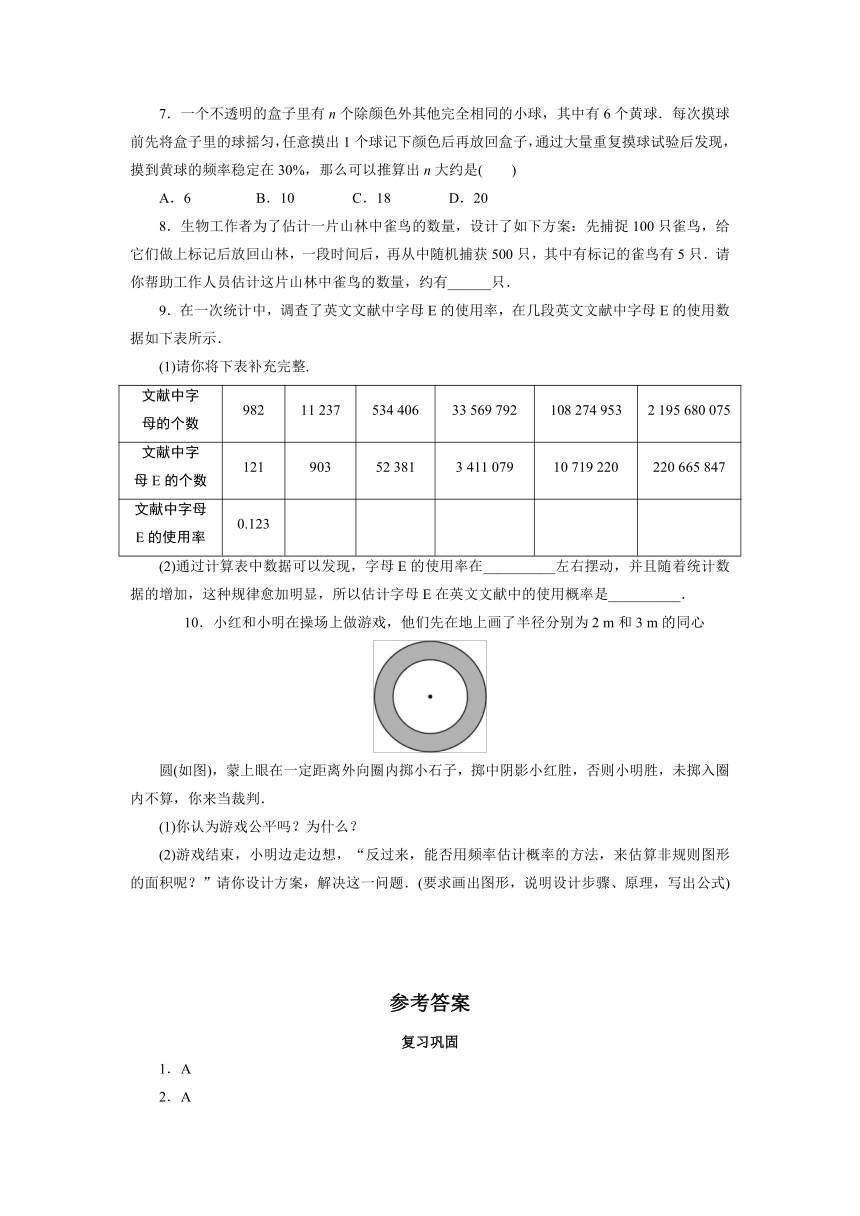
10.小红和小明在操场上做游戏,他们先在地上画了半径分别为2 m和3 m的同心
圆(如图),蒙上眼在一定距离外向圈内掷小石子,掷中阴影小红胜,否则小明胜,未掷入圈内不算,你来当裁判.
(1)你认为游戏公平吗?为什么?
(2)游戏结束,小明边走边想,“反过来,能否用频率估计概率的方法,来估算非规则图形的面积呢?”请你设计方案,解决这一问题.(要求画出图形,说明设计步骤、原理,写出公式)
参考答案
复习巩固
1.A
2.A
3.B 在随机抽取的20袋食盐中,质量在497.5 g~501.5 g之间的有5袋,由此可以估计任买1袋该摊位的食盐,质量在497.5 g~501.5 g之间的概率为.
4.30%
5.接近
6.解:(1)“3点朝上”出现的频率是;
“5点朝上”出现的频率是.
(2)小颖的说法是错误的.这是因为“5点朝上”的频率最大并不能说明“5点朝上”这一事件发生的概率最大.只有当试验的次数足够多时,该事件发生的频率才稳定在事件发生的概率附近.
小红的判断也是错误的,因为事件发生具有随机性,故“6点朝上”的次数不一定是100次.
(3)列表如下:
( http: / / www.21cnjy.com )
P(点数之和为3的倍数).
能力提升
7.D 由题意可得×100%=30%,解得n=20.故估计n大约是20.
8.10 000
9.(1)0.080 0.098 0.102 0.099 0.100
(2)0.100 0.100
10.解:(1)不公平.
因为P阴影=,
即小红胜的概率为,小明胜的概率为,
所以游戏对双方不公平.
(2)能利用频率估计概率的试验方法估算非规则图形的面积.
设计方案:①设计一个可测量面积的规则图形将非规则图形围起来(如正方形,其面积为S),如图所示;
( http: / / www.21cnjy.com )
②往图形中掷点(如蒙上眼往图形中随意掷石子,掷在图外不做记录);
③当掷点数充分大(如1万次)时,记录并统计结果,设掷入正方形内n次,其中m次掷入图形内;
④设非规则图形的面积为S1,用频率估计概率,即掷入非规则图形内的频率为≈P(掷入非规则图形内)=,故≈ S1≈.
复习巩固
1.已知抛一枚均匀硬币正面朝上的概率为,则下列说法中,错误的是( )
A.连续抛一枚均匀硬币2次必有1次正面朝上
B.连续抛一枚均匀硬币10次都可能正面朝上
C.大量反复抛一枚均匀硬币,平均每100次出现正面朝上50次
D.通过抛一枚均匀硬币确定谁先发球的比赛规则是公平的
2.在一盒子里有红、黄、蓝球共100个, ( http: / / www.21cnjy.com )小明总结多次摸球的规律:红球、黄球、蓝球的概率依次是35%,25%,40%,则估计红、黄、蓝球的个数分别是( )
A.35,25,40 B.40,25,35
C.35,40,25 D.40,35,25
3.在一次质检抽测中,随机抽取某摊位20袋食盐,测得各袋的质量分别为(单位:g):
492 496 494 495 498 497 501 502
504 496 497 503 506 508 507 492
496 500 501 499
根据以上抽测结果,任买1袋该摊位的食盐,质量在497.5 g~501.5 g之间的概率为( )
A. B.
C. D.
4.某射手在同一条件下,射击200次,击中靶心100次,射击400次,击中靶心121次,射击800次,击中靶心240次,则该射手射击一次击中靶心的概率约为__________.
5.在“抛掷正六面体”的试验中,如果正六面体的六个面上分别标有数字1,2,3,4,5和6,随着试验的次数增多,出现数字“1”的频率的变化趋势是__________.
6.小颖和小红两位同学在学习“概率”时,做了抛掷骰子(质地均匀的正方体)试验,她们共做了60次,试验的结果如下:
朝上的点数 1 2 3 4 5 6
出现的次数 7 9 6 8 20 10
(1)计算“3点朝上”的频率和“5点朝上”的频率.
(2)小颖说:“根据试验,一次试验中出现5 ( http: / / www.21cnjy.com )点朝上的概率最大”;小红说:“如果抛掷600次,那么出现6点朝上的次数正好是100次.”小颖和小红的说法正确吗?为什么?
(3)小颖和小红各抛掷一枚骰子,用列表或画树状图的方法求出两个骰子朝上的点数之和为3的倍数的概率.
能力提升
7.一个不透明的盒子里有n个除颜色外其他完全相同的小球,其中有6个黄球.每次摸球前先将盒子里的球摇匀,任意摸出1个球记下颜色后再放回盒子,通过大量重复摸球试验后发现,摸到黄球的频率稳定在30%,那么可以推算出n大约是( )
A.6 B.10 C.18 D.20
8.生物工作者为了估计一片山林中雀鸟的数量,设计了如下方案:先捕捉100只雀鸟,给它们做上标记后放回山林,一段时间后,再从中随机捕获500只,其中有标记的雀鸟有5只.请你帮助工作人员估计这片山林中雀鸟的数量,约有______只.
9.在一次统计中,调查了英文文献中字母E的使用率,在几段英文文献中字母E的使用数据如下表所示.
(1)请你将下表补充完整.
文献中字母的个数 982 11 237 534 406 33 569 792 108 274 953 2 195 680 075
文献中字母E的个数 121 903 52 381 3 411 079 10 719 220 220 665 847
文献中字母E的使用率 0.123
(2)通过计算表中数据可以发现,字母E的使 ( http: / / www.21cnjy.com )用率在__________左右摆动,并且随着统计数据的增加,这种规律愈加明显,所以估计字母E在英文文献中的使用概率是__________.
10.小红和小明在操场上做游戏,他们先在地上画了半径分别为2 m和3 m的同心
圆(如图),蒙上眼在一定距离外向圈内掷小石子,掷中阴影小红胜,否则小明胜,未掷入圈内不算,你来当裁判.
(1)你认为游戏公平吗?为什么?
(2)游戏结束,小明边走边想,“反过来,能否用频率估计概率的方法,来估算非规则图形的面积呢?”请你设计方案,解决这一问题.(要求画出图形,说明设计步骤、原理,写出公式)
参考答案
复习巩固
1.A
2.A
3.B 在随机抽取的20袋食盐中,质量在497.5 g~501.5 g之间的有5袋,由此可以估计任买1袋该摊位的食盐,质量在497.5 g~501.5 g之间的概率为.
4.30%
5.接近
6.解:(1)“3点朝上”出现的频率是;
“5点朝上”出现的频率是.
(2)小颖的说法是错误的.这是因为“5点朝上”的频率最大并不能说明“5点朝上”这一事件发生的概率最大.只有当试验的次数足够多时,该事件发生的频率才稳定在事件发生的概率附近.
小红的判断也是错误的,因为事件发生具有随机性,故“6点朝上”的次数不一定是100次.
(3)列表如下:
( http: / / www.21cnjy.com )
P(点数之和为3的倍数).
能力提升
7.D 由题意可得×100%=30%,解得n=20.故估计n大约是20.
8.10 000
9.(1)0.080 0.098 0.102 0.099 0.100
(2)0.100 0.100
10.解:(1)不公平.
因为P阴影=,
即小红胜的概率为,小明胜的概率为,
所以游戏对双方不公平.
(2)能利用频率估计概率的试验方法估算非规则图形的面积.
设计方案:①设计一个可测量面积的规则图形将非规则图形围起来(如正方形,其面积为S),如图所示;
( http: / / www.21cnjy.com )
②往图形中掷点(如蒙上眼往图形中随意掷石子,掷在图外不做记录);
③当掷点数充分大(如1万次)时,记录并统计结果,设掷入正方形内n次,其中m次掷入图形内;
④设非规则图形的面积为S1,用频率估计概率,即掷入非规则图形内的频率为≈P(掷入非规则图形内)=,故≈ S1≈.
同课章节目录
