冀教版七年级数学下学期期中达标测评卷(A卷)(含解析)
文档属性
| 名称 | 冀教版七年级数学下学期期中达标测评卷(A卷)(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 527.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-04-18 00:00:00 | ||
图片预览



文档简介
冀教版七年级数学下学期期中达标测评卷(A卷)
【满分120分 考试时间120分钟】
一、选择题(本大题共10小题,每小题3分,共30分.在每小题给出的四个选项中,只有一项是符合题目要求的)
1.中国倡导的“一带一路”建设将促进我国与世界各国的互利合作,据统计“一带一路”地区覆盖总人口约为4400000000人,这个数用科学记数法表示是( )
A.人 B.人 C.人 D.人
2.如图直线AB,CD被EF所截,图中标注的角中是同位角的是( )
A.∠1与∠3 B.∠2与∠6 C.∠3与∠8 D.∠4与∠7
3.对于方程组用加减法消去x得到的方程为( )
A. B. C. D.
4.下列语句中,
①有公共顶点且相等的角是对顶角;
②直线外一点到这条直线的垂线段,叫做点到直线的距离;
③平行于同一条直线的两条直线平行;
④经过一点有且只有一条直线与已知直线垂直.其中正确的有( )
A.1个 B.2个 C.3个 D.4个
5.已知是关于x、y的二元一次方程组的解,则△和?代表的数分别是( )
A.3和 B.和3 C.1和5 D.5和1
6.下列运算正确的是( )
A. B. C. D.
7.小华在利用完全平方公式计算一个二项整式的平方时,不小心用墨水把中间一项的系数染黑了,得到正确的结果为,则中间一项的系数是( )
A. B. C.或 D.
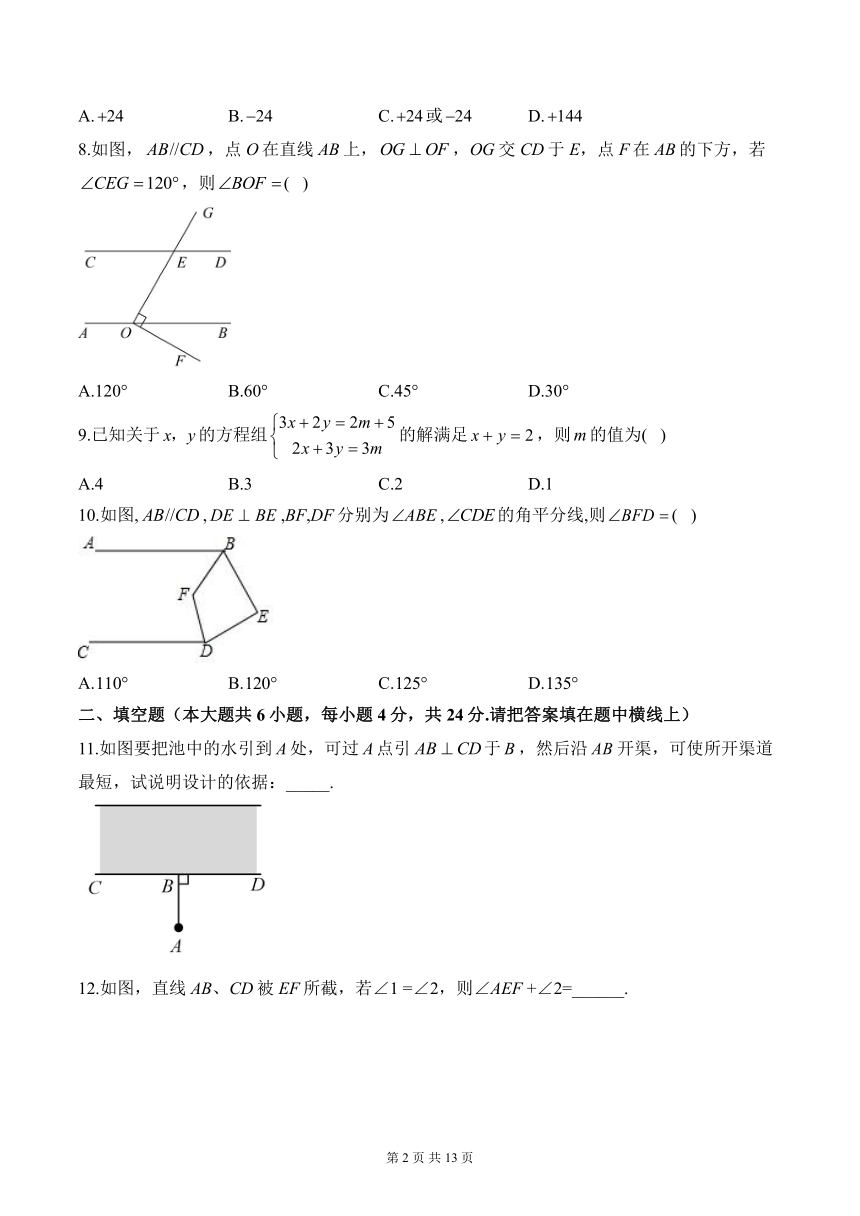
8.如图,,点O在直线AB上,,OG交CD于E,点F在AB的下方,若,则( )
A.120° B.60° C.45° D.30°
9.已知关于的方程组的解满足,则的值为( )
A.4 B.3 C.2 D.1
10.如图,,,BF,DF分别为,的角平分线,则( )
A. B. C. D.
二、填空题(本大题共6小题,每小题4分,共24分.请把答案填在题中横线上)
11.如图要把池中的水引到处,可过点引于,然后沿开渠,可使所开渠道最短,试说明设计的依据:_____.
12.如图,直线AB、CD被EF所截,若∠1 =∠2,则∠AEF +∠2=______.
13.化简:________________.
14.,则m的值为___________.
15.已知和都是方程的解,则_______,_______.
16.如图,,BF,DF分别平分和,,与互补,则的度数为______.
三、解答题(本大题共8小题,共66分.解答应写出必要的文字说明,证明过程或演算步骤)
17.(6分)解方程组:
(1)
(2)
18.(6分)某文具店用13600元购进了一批篮球和排球,共计500个,它们的成本价和销售价如表所示:
单价(元/个) 成本价 销售价
篮球 32 48
排球 24 36
(1)购进的这批篮球和排球各多少个?
(2)该店销售完这批篮球和排球后可获利多少元?
19.(7分)(1)已知,,求的值.
(2)已知,,求的值;
20.(7分)如图,,直线分别交、于点E、F,平分,若,求的度数.
21.(8分)计算:
(1);
(2)先化简,再求值,其中.
22.(10分)已知:如图,平分,且于点D,,请在括号中补全步骤的推理理由.
(1)证明;
证明:(___________)
,(___________).
又(___________),
(___________),
,,
又平分(___________),
(___________),
(___________),
(___________).
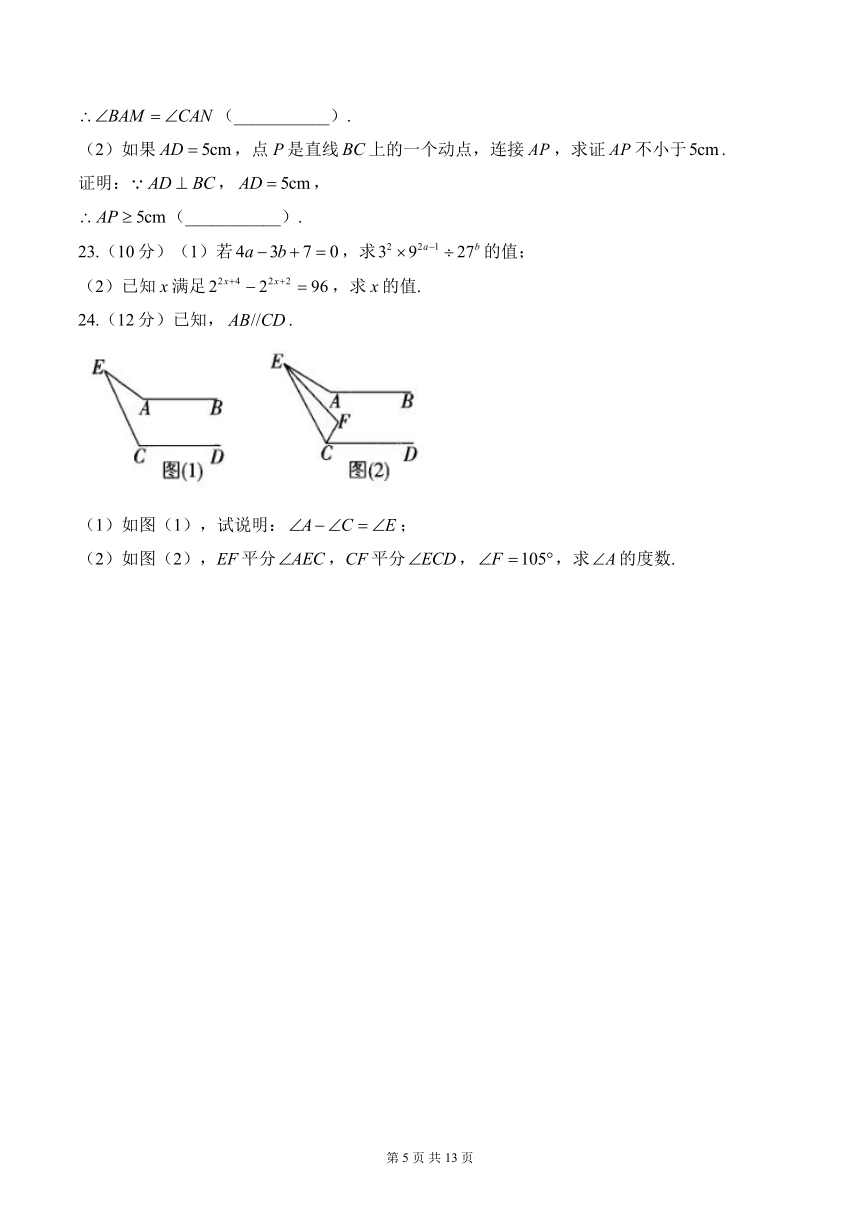
(2)如果,点P是直线上的一个动点,连接,求证不小于.
证明:,,
(___________).
23.(10分)(1)若,求的值;
(2)已知x满足,求x的值.
24.(12分)已知,.
(1)如图(1),试说明:;
(2)如图(2),EF平分,CF平分,,求的度数.
答案以及解析
1.答案:C
解析:.
故选C.
2.答案:D
解析:同位角是∠4与∠7,
故选:D.
3.答案:C
解析:由得:,
即
故选:C.
4.答案:A
解析:①有公共顶点且两边互为反向延长线的两个角是对顶角,故该说法错误;
②直线外一点到这条直线的垂线段的长度,叫做点到直线的距离,故该说法错误;
③平行于同一直线的两直线平行,正确;
④同一平面内,经过一点有且只有一条直线与已知直线垂直,故该说法错误.
故正确的有1个,
故选:A.
5.答案:D
解析:
将代入①得,
,
解得:,
,
△和?代表的数分别是5和1;
故选:D.
6.答案:D
解析:A选项中不是同类项,无法合并,故错误;
B选项中,,故错误;
C选项中,,故错误;
D选项计算正确;
故选:D.
7.答案:C
解析:依题意,,
则中间一项的系数是或,能使左右两边相等,
即,
或,
故选:C.
8.答案:D
解析:,
,
,
,
即,
.
故选:D.
9.答案:D
解析:,
由①②得到,
∴,
∵,∴,解得,
故选:D.
10.答案:D
解析:如图所示,过E作,
,,
,,
,
,,
BFDF分别为,的角平分线,
四边形BFDF中
,
故选:D
11.答案:垂线段最短
解析:由题意,得:设计的依据为:点到直线的距离,垂线段最短;
故答案为:垂线段最短.
12.答案:
解析:因为,所以,所以,
故答案为:.
13.答案:
解析:,
故答案为:.
14.答案:
解析:因为,所以,所以,解得.
15.答案:4;
解析:和都是方程的解,
将和带入成立,
得:,
解得:
.
故答案为:4;
16.答案:
解析:如图延长FB交CD于G
∵BF∥ED∴∠F=∠EDF
又∵DF平分∠CDE,∴∠CDE=2∠F,
∵BF∥ED∴∠CGF=∠CDE=2∠F,
∵AB∥CD∴∠ABF=∠CGF=2∠F,
∵BF平分∠ABE∴∠ABE=2∠ABF=4∠F,
又∵∠F与∠ABE互补∴∠F+∠ABE=180°即5∠F=180°,
解得∠F=36°
故答案为36°.
17.答案:(1)
(2)
解析:(1)
整理得,
得,
解得
将代入①得,
解得
原方程组的解为;
(2)
由①得,
将④代入②,③得,
整理得,
得,
解得,
将代入⑤得,
解得,
将,代入④得,
原方程组的解为.
18.答案:(1)购进的这批篮球有200个,排球有300个
(2)可获利6800元
解析:(1)设购进的这批篮球有个,排球有个,
由题意得:,
解得,
答:购进的这批篮球有200个,排球有300个.
(2)(元),
答:该店销售完这批篮球和排球后可获利6800元.
19.答案:(1)576
(2)28
解析:(1),,
;
(2),,
.
20.答案:
解析:,,,
,,
平分,,
.
21.答案:(1)
(2),11
解析:(1)
.
(2)原式,
当时,.
22.答案:(1)已知;两直线平行,内错角相等;已知;垂直的定义;已知;角平分线的定义;等角的余角相等;等量代换
(2)垂线段最短
解析:(1)证明:(已知),
,
(两直线平行,内错角相等).
又(已知),
(垂直的定义),
,,
又平分(已知),
(角平分线的定义),
(等角的余角相等),
(等量代换).
故答案为:已知;两直线平行,内错角相等;已知;垂直的定义;已知;角平分线的定义;等角的余角相等;等量代换.
(2)证明:,,
(垂线段最短).
故答案为:垂线段最短.
23.答案:(1)
(2)
解析:(1)原式.
因为,所以,所以原式.
(2),,,,,所以,解得.
24.答案:(1)见解析
(2)
解析:(1)如图(1),延长EA交CD于点M.
因为,所以.
因为,所以,
所以.
(2)如图(2),过点E作,过点F作.
因为,所以,
所以,,.
因为EF平分,CF平分.
所以,,
所以,,
所以,
所以,
即.
由(1)知,,
所以,所以,
所以.
(
第
1
页 共
14
页
)
【满分120分 考试时间120分钟】
一、选择题(本大题共10小题,每小题3分,共30分.在每小题给出的四个选项中,只有一项是符合题目要求的)
1.中国倡导的“一带一路”建设将促进我国与世界各国的互利合作,据统计“一带一路”地区覆盖总人口约为4400000000人,这个数用科学记数法表示是( )
A.人 B.人 C.人 D.人
2.如图直线AB,CD被EF所截,图中标注的角中是同位角的是( )
A.∠1与∠3 B.∠2与∠6 C.∠3与∠8 D.∠4与∠7
3.对于方程组用加减法消去x得到的方程为( )
A. B. C. D.
4.下列语句中,
①有公共顶点且相等的角是对顶角;
②直线外一点到这条直线的垂线段,叫做点到直线的距离;
③平行于同一条直线的两条直线平行;
④经过一点有且只有一条直线与已知直线垂直.其中正确的有( )
A.1个 B.2个 C.3个 D.4个
5.已知是关于x、y的二元一次方程组的解,则△和?代表的数分别是( )
A.3和 B.和3 C.1和5 D.5和1
6.下列运算正确的是( )
A. B. C. D.
7.小华在利用完全平方公式计算一个二项整式的平方时,不小心用墨水把中间一项的系数染黑了,得到正确的结果为,则中间一项的系数是( )
A. B. C.或 D.
8.如图,,点O在直线AB上,,OG交CD于E,点F在AB的下方,若,则( )
A.120° B.60° C.45° D.30°
9.已知关于的方程组的解满足,则的值为( )
A.4 B.3 C.2 D.1
10.如图,,,BF,DF分别为,的角平分线,则( )
A. B. C. D.
二、填空题(本大题共6小题,每小题4分,共24分.请把答案填在题中横线上)
11.如图要把池中的水引到处,可过点引于,然后沿开渠,可使所开渠道最短,试说明设计的依据:_____.
12.如图,直线AB、CD被EF所截,若∠1 =∠2,则∠AEF +∠2=______.
13.化简:________________.
14.,则m的值为___________.
15.已知和都是方程的解,则_______,_______.
16.如图,,BF,DF分别平分和,,与互补,则的度数为______.
三、解答题(本大题共8小题,共66分.解答应写出必要的文字说明,证明过程或演算步骤)
17.(6分)解方程组:
(1)
(2)
18.(6分)某文具店用13600元购进了一批篮球和排球,共计500个,它们的成本价和销售价如表所示:
单价(元/个) 成本价 销售价
篮球 32 48
排球 24 36
(1)购进的这批篮球和排球各多少个?
(2)该店销售完这批篮球和排球后可获利多少元?
19.(7分)(1)已知,,求的值.
(2)已知,,求的值;
20.(7分)如图,,直线分别交、于点E、F,平分,若,求的度数.
21.(8分)计算:
(1);
(2)先化简,再求值,其中.
22.(10分)已知:如图,平分,且于点D,,请在括号中补全步骤的推理理由.
(1)证明;
证明:(___________)
,(___________).
又(___________),
(___________),
,,
又平分(___________),
(___________),
(___________),
(___________).
(2)如果,点P是直线上的一个动点,连接,求证不小于.
证明:,,
(___________).
23.(10分)(1)若,求的值;
(2)已知x满足,求x的值.
24.(12分)已知,.
(1)如图(1),试说明:;
(2)如图(2),EF平分,CF平分,,求的度数.
答案以及解析
1.答案:C
解析:.
故选C.
2.答案:D
解析:同位角是∠4与∠7,
故选:D.
3.答案:C
解析:由得:,
即
故选:C.
4.答案:A
解析:①有公共顶点且两边互为反向延长线的两个角是对顶角,故该说法错误;
②直线外一点到这条直线的垂线段的长度,叫做点到直线的距离,故该说法错误;
③平行于同一直线的两直线平行,正确;
④同一平面内,经过一点有且只有一条直线与已知直线垂直,故该说法错误.
故正确的有1个,
故选:A.
5.答案:D
解析:
将代入①得,
,
解得:,
,
△和?代表的数分别是5和1;
故选:D.
6.答案:D
解析:A选项中不是同类项,无法合并,故错误;
B选项中,,故错误;
C选项中,,故错误;
D选项计算正确;
故选:D.
7.答案:C
解析:依题意,,
则中间一项的系数是或,能使左右两边相等,
即,
或,
故选:C.
8.答案:D
解析:,
,
,
,
即,
.
故选:D.
9.答案:D
解析:,
由①②得到,
∴,
∵,∴,解得,
故选:D.
10.答案:D
解析:如图所示,过E作,
,,
,,
,
,,
BFDF分别为,的角平分线,
四边形BFDF中
,
故选:D
11.答案:垂线段最短
解析:由题意,得:设计的依据为:点到直线的距离,垂线段最短;
故答案为:垂线段最短.
12.答案:
解析:因为,所以,所以,
故答案为:.
13.答案:
解析:,
故答案为:.
14.答案:
解析:因为,所以,所以,解得.
15.答案:4;
解析:和都是方程的解,
将和带入成立,
得:,
解得:
.
故答案为:4;
16.答案:
解析:如图延长FB交CD于G
∵BF∥ED∴∠F=∠EDF
又∵DF平分∠CDE,∴∠CDE=2∠F,
∵BF∥ED∴∠CGF=∠CDE=2∠F,
∵AB∥CD∴∠ABF=∠CGF=2∠F,
∵BF平分∠ABE∴∠ABE=2∠ABF=4∠F,
又∵∠F与∠ABE互补∴∠F+∠ABE=180°即5∠F=180°,
解得∠F=36°
故答案为36°.
17.答案:(1)
(2)
解析:(1)
整理得,
得,
解得
将代入①得,
解得
原方程组的解为;
(2)
由①得,
将④代入②,③得,
整理得,
得,
解得,
将代入⑤得,
解得,
将,代入④得,
原方程组的解为.
18.答案:(1)购进的这批篮球有200个,排球有300个
(2)可获利6800元
解析:(1)设购进的这批篮球有个,排球有个,
由题意得:,
解得,
答:购进的这批篮球有200个,排球有300个.
(2)(元),
答:该店销售完这批篮球和排球后可获利6800元.
19.答案:(1)576
(2)28
解析:(1),,
;
(2),,
.
20.答案:
解析:,,,
,,
平分,,
.
21.答案:(1)
(2),11
解析:(1)
.
(2)原式,
当时,.
22.答案:(1)已知;两直线平行,内错角相等;已知;垂直的定义;已知;角平分线的定义;等角的余角相等;等量代换
(2)垂线段最短
解析:(1)证明:(已知),
,
(两直线平行,内错角相等).
又(已知),
(垂直的定义),
,,
又平分(已知),
(角平分线的定义),
(等角的余角相等),
(等量代换).
故答案为:已知;两直线平行,内错角相等;已知;垂直的定义;已知;角平分线的定义;等角的余角相等;等量代换.
(2)证明:,,
(垂线段最短).
故答案为:垂线段最短.
23.答案:(1)
(2)
解析:(1)原式.
因为,所以,所以原式.
(2),,,,,所以,解得.
24.答案:(1)见解析
(2)
解析:(1)如图(1),延长EA交CD于点M.
因为,所以.
因为,所以,
所以.
(2)如图(2),过点E作,过点F作.
因为,所以,
所以,,.
因为EF平分,CF平分.
所以,,
所以,,
所以,
所以,
即.
由(1)知,,
所以,所以,
所以.
(
第
1
页 共
14
页
)
同课章节目录
