19.3课题学习-选择方案-—次函数的实际应用-方案选择问题 专题提升训练(含解析)2023—2024学年人教版八年级数学下册
文档属性
| 名称 | 19.3课题学习-选择方案-—次函数的实际应用-方案选择问题 专题提升训练(含解析)2023—2024学年人教版八年级数学下册 |

|
|
| 格式 | docx | ||
| 文件大小 | 196.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-04-17 19:52:55 | ||
图片预览




文档简介
2023-2024学年人教版八年级数学下册《19.3课题学习-选择方案-—次函数的实际应用-方案选择问题》专题提升训练(附答案)
一、单选题
1.已知某租车公司有A,B两种租车方案:A方案为先支付500元,再按每千米元收费;B方案直接按每千米1元收费,已知小明租车花费了800元,若他使用的是最优租车方案,则他的行驶里程是( )
A.600千米 B.700千米 C.800千米 D.900千米
2.暑假里父母带小明外出旅行,了解到东方旅行社规定:若父母各买一张全票,则孩子的 费用可按全票价七折优惠(即优惠30%);而光明旅行社规定:三人旅行可按团体票计价,即按全票价的90%收费,若已知旅行社的全票价相同,则实际收费( )
A.东方旅行社比光明旅行社低
B.东方旅行社与光明旅行社相同
C.东方旅行社比光明旅行社高
D.谁高谁低视全票价多少而定
3.某学校计划租用甲、乙两种客车送240名师生(其中学生233名、教师7名)集体外出活动,要求每辆客车上至少要有1名教师.甲、乙两种客车的载客量和租金如下表:
甲种客车 乙种客车
载客量(单位:人/辆) 45 30
租金(单位:元/辆) 400 280
则最节省费用的租车方案是( )
A.租甲种车4辆,租乙种车2辆 B.租甲种车5辆,租乙种车1辆
C.租甲种车2辆,租乙种车5辆 D.租甲种车3辆,租乙种车4辆
4.水果店购买一种葡萄所付款金额(元)与购买量(千克)情况如图,萌萌一次购买6千克这种葡萄比她分三次购买每次购2千克这种葡萄可节省( )元.
A.18 B.12 C.9 D.6
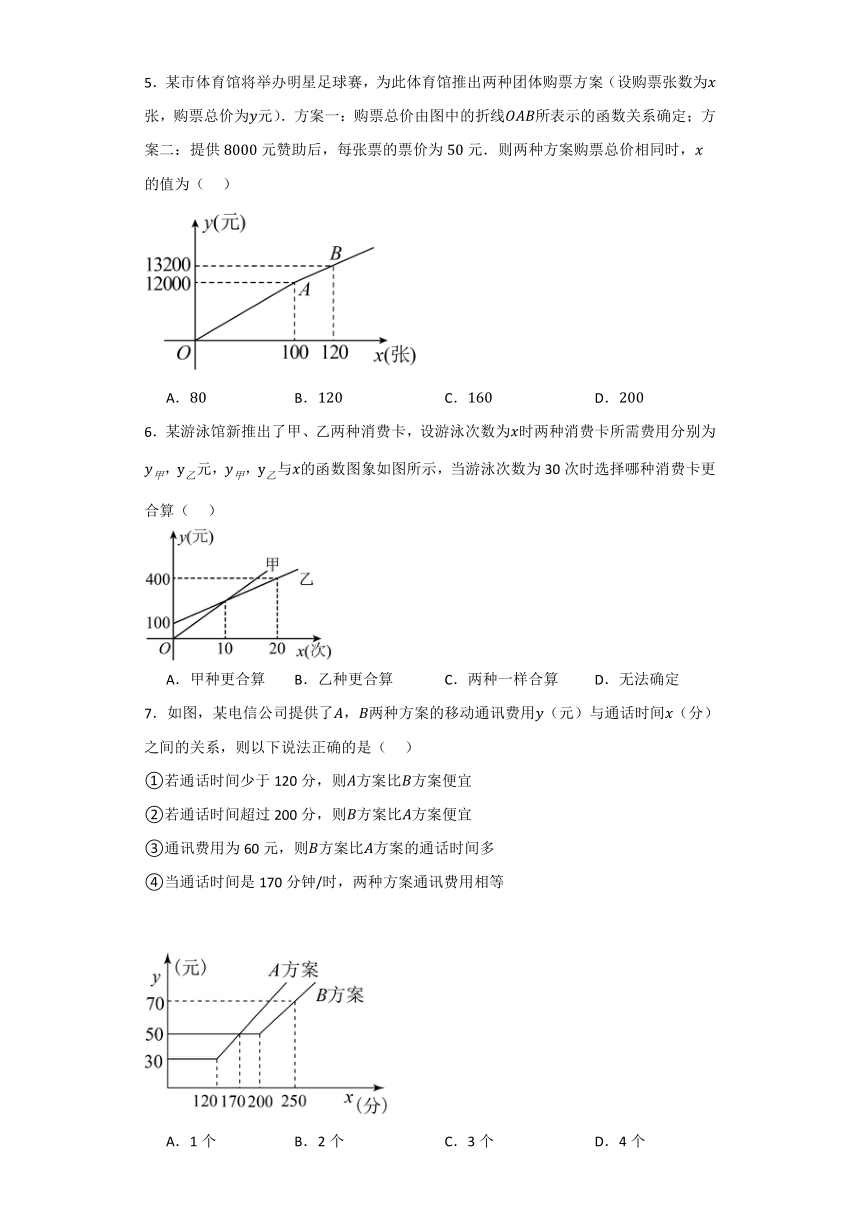
5.某市体育馆将举办明星足球赛,为此体育馆推出两种团体购票方案(设购票张数为张,购票总价为元).方案一:购票总价由图中的折线所表示的函数关系确定;方案二:提供元赞助后,每张票的票价为元.则两种方案购票总价相同时,的值为( )
A. B. C. D.
6.某游泳馆新推出了甲、乙两种消费卡,设游泳次数为时两种消费卡所需费用分别为,元,,与的函数图象如图所示,当游泳次数为30次时选择哪种消费卡更合算( )
A.甲种更合算 B.乙种更合算 C.两种一样合算 D.无法确定
7.如图,某电信公司提供了,两种方案的移动通讯费用(元)与通话时间(分)之间的关系,则以下说法正确的是( )
①若通话时间少于120分,则方案比方案便宜
②若通话时间超过200分,则方案比方案便宜
③通讯费用为60元,则方案比方案的通话时间多
④当通话时间是170分钟/时,两种方案通讯费用相等
A.1个 B.2个 C.3个 D.4个
二、填空题
8.假期学校组织360名师生外出旅游,某客车出租公司有两种大客车可供选择:甲种客车每辆车有40个座,租金400元;乙种客车每辆车有50个座,租金480元.则租用该公司客车最少需用租金 元.
9.A城有种农机30台,B城有该农机40台,现要将这些农机全部运往C,D两乡,调运任务承包给某运输公司.已知C乡需要农机34台,D乡需要农机36台,从A城往C,D两乡运送农机的费用分别为250元/台和200元/台,从B城往C,D两乡运送农机的费用分别为150元/台和240元/台.设A城运往C乡该农机x台,运送全部农机的总费用为W元,则W关于x的函数关系式为 .
10.2019年1月18日,重庆经开区新时代文明实践“五进企业”系列活动----2019年新春游园会成功矩形,这次新春游园会的门票分为个人票和团体票两大类其中个人票设置有三种,票得种类 夜票(A) 平日普通票(B)指定日普通票(C)某社区居委会欲购买个人票100张,其中B种票的张数是A种票的3倍还多8张,设购买A种票的张数为x,C种票张数为y,则化简后y与x之间的关系式为: (不必写出x的取值范围)
11.某公司为用户提供上网服务的两种收费方式如下表:
收费标准/方式 基础费用(单位:元/月) 单价(单位:元/分)
A 0 0.1
B 20 0.05
若设用户每月上网的时间为x分钟,A,B两种收费方式的费用分别为(元)、(元),则当每月上网时间多于400分钟时,选择 种方式省钱(填“A”或“B”).
12.小静准备到甲或乙商场购买一些商品,两商场同种商品的标价相同,而各自推出不同的优惠方案:在甲商场累计购买满一定数额a元后,再购买的商品按原价的收费;在乙商场累计购买50元商品后,再购买的商品按原价的收费.若累计购物x元,当时,在甲商场需付钱数,当时,在乙商场需付钱数为.下列说法:①;②当累计购物大于50元时,选择乙商场一定优惠些;③当累计购物超过150元时,选择甲商场一定优惠些;④.其中正确的说法是 (填序号)
13.本年度某单位常有集体外出学习活动,因此准备与出租车公司签订租车协议.现有甲、乙两家出租车公司供选择.设每月行驶千米,应付给甲公司元,应付给乙公司元,、分别与之间的函数关系如图所示,若这个单位估计每月需要行驶的路程为3500千米,那么为了省钱,这个单位应租 公司.
三、解答题
14.甲、乙两商场出售相同的某种商品,每件售价均为3000元,并且多买都有一定的优惠.甲商场的优惠条件是:第一件按原价收费,其余每件优惠;乙商场的优惠条件是:每件优惠.设所买商品为()件,甲商场收费为元,乙商场收费为元.
(1)分别求出,与之间的关系式;
(2)当所买商品为5件时,选择哪家商场更优惠?请说明理由.
15.某零件制造车间有工人20名,已知每名工人每天可制造甲种零件6个或乙种零件5个,且每制造一个甲种零件可获利150元,每制造一个乙种零件可获利260元,在这20名工人中,设该车间每天安排x名工作制造甲种零件,其余工人制造乙种零件.
(1)请写出此车间每天所获利润y(元)与x(人)之间的函数关系式;
(2)若只考虑利润问题,要使每天所获利润不低于24000元,你认为至多要派多少名工人制造甲种零件才合适?
16.某公司要印制大运会这传材料,甲印刷厂提出:每份材料收1元印制费,另收元制版费:乙印刷厂提出:每份材料收3元印制费,不收制版费.
(1)分别写出两印刷厂的收费y(元)与印制数量x(份)之间的关系式;
请你用自己的方法,回答下列问题:
(2)印刷份宣传材料时,选择哪家印刷厂比较合算?
(3)该公司拟拿出元用于印制宣传材料,找哪家印刷厂印制宣传材料能多一些?
17.随着生活水平的日益提高,人们的健康意识逐渐增强,越来越多的人把健身作为一种时尚的生活方式,某商家抓住机遇推出促销活动,向客户提供了两种优惠方案:
方案一:买一件运动外套送一件卫衣;
方案二:运动外套和卫衣均在定价的基础上打8折.
运动外套每件定价300元,卫衣每件定价100元.在开展促销活动期间,某俱乐部要到该商场购买运动外套100件,卫衣件().
(1)方案一需付款:______元,方案二需付款:______元;
(2)当时,请计算并比较这两种方案哪种更划算;
(3)当时,如果两种方案可以组合使用,你能帮助俱乐部设计一种最省钱的方案吗?请直接写出你的方案.
18.某游泳馆夏季推出两种游泳付费方式.方式一:先购买会员证,每张会员证100元,只限本人当年使用,凭证游泳每次再付费15元;方式二:不购买会员证,每次游泳付费20元.设小明计划今年夏季游泳次数为x次(x为正整数).
(1)根据题意,将表格填写完整.
游泳次数 10 15 20 …
采用方式一付费(元) 250 325 __ …
采用方式二付费(元) 200 __ 400 …
(2)设方式一的总费用为元,方式二的总费用为元,分别用x表示和;
(3)通过计算说明,当和时,分别应选择哪种付费方式较合算?
19.某超市鸡蛋供应紧张,需每天从外地调运鸡蛋千克.超市决定从甲、乙两大型养殖场调运鸡蛋,已知甲养殖场每天最多可调出千克,乙养殖场每天最多可调出千克,从甲、乙两养殖场调运鸡蛋到该超市的路程和运费如表:
到超市的路程(千米) 运费(元/千克·千米)
甲养殖场
乙养殖场
设从甲养殖场调运鸡蛋千克,总运费为元.
(1)从甲养殖场调运鸡蛋的运费,用代数式表示为______,从乙养殖场需要调运鸡蛋的数量,用代数式表示为______;
(2)试写出与的函数关系式;
(3)请求出自变量取值范围,说明怎样安排调运方案才能使每天的总运费最少?
20.为响应政府低碳生活,绿色出行的号召,某公交公司决定购买一批节能环保的新能源公交车,计划购买型和型两种公交车,其中每辆的价格、年载客量如表:
型 型
价格(万元/辆)
年载客量(万人/年) 60 100
若购买型公交车1辆,型公交车2辆,共需400万元;若购买型公交车2辆,型公交车1辆,共需350万元.
(1)求,的值;
(2)计划购买型和型两种公交车共10辆,如果该公司购买型和型公交车的总费用不超过1200万元,且确保这10辆公交车在该线路的年均载客总和不少于640万人次,问有几种购买方案
(3)在(2)的条件下,请用一次函数的性质说明哪种方案使得购车总费用最少 最少费用是多少万元
参考答案
1.解:设小明行驶里程是x千米,需要花费y元,
A方案:一共需要花费:,
B方案∶ 一共需要花费:,
若选择A方案,,解得:,
若选择B方案,得,
由于,则选择B方案是最优租车方案,行驶里程为800米,
故选:C.
2.解:依题意设旅行社全票价为x元,三人旅行实际收费为y元.可知东方旅行社三人旅行实际收费为:y=2x+70%x=2.7x(元)而光明旅行社三人旅行实际收费为:=2.7x.可知两家旅行社实际收费相同.
3.解:设租用甲客车x辆,租车总费用y元,由每辆客车上至少要有1名教师可知客车总数不能大于7辆,
要保证240名师生有车坐,客车总数不能小于,客车总数不能小于6,
∴客车总数为6,,
由题意可得,,
整理可得,
由题意,,
解得,
∵,
∴,
∵中,,y随x的增大而增大,
∴x取最小值时,即,y有最小值,
即当租甲种车4辆,租乙种车2辆,费用最少,
故选:A.
4.解:设直线AB的解析式为,
将(2,38)、(4,70)代入得,,
解得:,
当时,,
即萌萌一次购买6千克这种葡萄需要元;
她分三次购买每次购2千克这种葡萄需要(元),
∴(元),
萌萌一次购买6千克这种葡萄比她分三次购买每次购2千克这种葡萄可节省12元.
故选:B.
5.解:在方案一中,设OA表示的解析式为,且
解得,
表示的解析式为:;
设表示的解析式为,
又,
解得,,
表示的解析式为:;
方案二的解析式为:;
当时,
故的图象与的图象无交点,
当时,,
所以,当时,两种方案购票总价相同.
故选:D.
6.解:利用图象,当游泳次数大于10次时,
在上面,即>,
∴当游泳次数为30次时,选择乙种方式省钱.
故选:B.
7.解:依题意得
A:(1)当0≤x≤120,yA=30,
(2)当x>120,yA=30+(x-120)×[(50-30)÷(170-120)]=0.4x-18;
B:(1)当0≤x<200,yB=50,
当x>200,yB=50+[(70-50)÷(250-200)](x-200)=0.4x-30,
所以当x≤120时,A方案比B方案便宜20元,故(1)正确;
当x≥200时,B方案比A方案便宜12元,故(2)正确;
当y=60时,A:60=0.4x-18,∴x=195,
B:60=0.4x-30,∴x=225,故(3)正确;
当A方案与B方案的费用相等,通话时间为170分钟,故(4)正确;
故选:D.
8.解:若只租甲种客车需要辆.若只租乙种客车需要8辆,因而两种客车用共租8辆.
设甲车有x辆,乙车有辆,则,
解得:,
整数解为1、2、3、4.
设汽车的租金为,
则:,即,
的值随的增大而减小,因而当时,最小.
故取,的最小值是3520元.
9.解:由题意得:因为A城运往C乡x台农机,则A城运往D乡(30﹣x)台农机,B城运往C乡(34﹣x)台农机,B城运往D乡[40﹣(34﹣x)]台农机
W=250x+200(30﹣x)+150(34﹣x)+240[40﹣(34﹣x)]
=140x+12540,
故答案为:W=140x+12540.
10.解:由题可知,,
∴.
故答案为.
11.解:由题意可知:=0.1x,=20+0.05x,
当=时,由0.1x=20+0.05x得:x=400,两种收费方式一样省钱;
当>时,由0.1x>20+0.05x得:x>400,B种方式省钱;
当<时,由0.1x<20+0.05x得:x<400,A种方式省钱,
∴当每月上网时间多于400分钟时,选择B种方式省钱,
故答案为:B.
12.解:①、,正确,符合题意;
②、当累计购物大于50时上没封顶,选择乙商场一定优惠显然不对,不符合题意;
③、当时,即,解之得.所以当累计购物超150元时,选择甲商场一定优惠些,符合题意;
④、根据题意,所以,符合题意;
故答案为:①③④.
13.解:根据图象可知当x>1500时,,此时甲省钱.
∵x=3500>1500,此时,
∴此时甲省钱.
故答案为:甲.
14.(1)解:由题意可得,
.
(2)当时,,
,
∵,
∴所买商品为5件时,应选择乙商场更优惠.
15.(1)解:设该车间每天安排x名工作制造甲种零件,则安排人制造乙种零件,
根据题意:
即;
(2)解:根据题意:令
解得:,
在中,
∵,
∴y的值随x的值的增大而减少,
∴要使,需,
答:至多要派5名工人制造甲种零件才合适.
16.解:(1)由题意得:甲厂收费y(元)与印制数量x(份)之间的关系式为,乙厂收费y(元)与印制数量x(份)之间的关系式为;
解:(2)当时,甲厂:(元);乙厂:(元).
∵
乙厂比较合算;
解:(3)当时,
甲厂:,解得(份);
乙厂:,解得(份),
∵.
甲厂印制宣传材料多一些.
17.(1)解:方案一∶ 购买运动外套100件,送100件卫衣,则还需购买件卫衣,
方案一需付款元;
方案二∶ 购买运动外套100件,卫衣x件,均打8折,
方案二 需付款元.
(2)当时,
方案一需付款:(元)
方案二需付款:(元)
(3)设购买a件运动外套使用方案一,则购买件运动外套使用方案二,
购买a件卫衣使用方案一,购买件卫衣使用方案二,
设总费用为w元,
则,
∵,费用w随着a的增大而减小.
∴当时,w取的最小值46000,即总费用最小,
∴最省钱的方案:按照方案一购买100件运动外套再按照方案二购买200件卫衣.
18.(1)解:当时,方式一:元,
当时,方式二:元;
(2)解:由题意,方式一的总费用:,
方式二的总费用:;
(3)解:当时,方式一:,
方式二:,
,方式二更划算;
当时,方式一:,
方式二:,
,方式一更划算.
综上所示,当时,选择方式二,当时,选择方式一.
19.解:(1)从甲养殖场调运鸡蛋千克,则从乙养殖场调运鸡蛋千克,
则从甲养殖场调运鸡蛋的运费为元,
故答案为:元,千克;
(2)由题意得,
与的函数关系式为;
(3)由题意得, ,,
,
由()知,
,
随的增大而增大,
当时,取得最小值,此时,
此时,
答:当从甲养殖场调运斤鸡蛋,从乙养殖场调运斤鸡蛋时,每天的总运费最省,总运费最低是元.
20.(1)解:依题意得:,解得:,
答:的值为100,的值为150;
(2)解:设购买型公交车辆,则购买型公交车辆,
依题意得:
解得:
又为整数
有4购买方案;
(3)解:设购车总费用为万元,
则,(且为整数)
,
随的增大而减小
当时,最小,最小值为(元),
购车总费用最少的方案是购买型公交车9辆,购买型公交车1辆,购车总费用为1050万元.
一、单选题
1.已知某租车公司有A,B两种租车方案:A方案为先支付500元,再按每千米元收费;B方案直接按每千米1元收费,已知小明租车花费了800元,若他使用的是最优租车方案,则他的行驶里程是( )
A.600千米 B.700千米 C.800千米 D.900千米
2.暑假里父母带小明外出旅行,了解到东方旅行社规定:若父母各买一张全票,则孩子的 费用可按全票价七折优惠(即优惠30%);而光明旅行社规定:三人旅行可按团体票计价,即按全票价的90%收费,若已知旅行社的全票价相同,则实际收费( )
A.东方旅行社比光明旅行社低
B.东方旅行社与光明旅行社相同
C.东方旅行社比光明旅行社高
D.谁高谁低视全票价多少而定
3.某学校计划租用甲、乙两种客车送240名师生(其中学生233名、教师7名)集体外出活动,要求每辆客车上至少要有1名教师.甲、乙两种客车的载客量和租金如下表:
甲种客车 乙种客车
载客量(单位:人/辆) 45 30
租金(单位:元/辆) 400 280
则最节省费用的租车方案是( )
A.租甲种车4辆,租乙种车2辆 B.租甲种车5辆,租乙种车1辆
C.租甲种车2辆,租乙种车5辆 D.租甲种车3辆,租乙种车4辆
4.水果店购买一种葡萄所付款金额(元)与购买量(千克)情况如图,萌萌一次购买6千克这种葡萄比她分三次购买每次购2千克这种葡萄可节省( )元.
A.18 B.12 C.9 D.6
5.某市体育馆将举办明星足球赛,为此体育馆推出两种团体购票方案(设购票张数为张,购票总价为元).方案一:购票总价由图中的折线所表示的函数关系确定;方案二:提供元赞助后,每张票的票价为元.则两种方案购票总价相同时,的值为( )
A. B. C. D.
6.某游泳馆新推出了甲、乙两种消费卡,设游泳次数为时两种消费卡所需费用分别为,元,,与的函数图象如图所示,当游泳次数为30次时选择哪种消费卡更合算( )
A.甲种更合算 B.乙种更合算 C.两种一样合算 D.无法确定
7.如图,某电信公司提供了,两种方案的移动通讯费用(元)与通话时间(分)之间的关系,则以下说法正确的是( )
①若通话时间少于120分,则方案比方案便宜
②若通话时间超过200分,则方案比方案便宜
③通讯费用为60元,则方案比方案的通话时间多
④当通话时间是170分钟/时,两种方案通讯费用相等
A.1个 B.2个 C.3个 D.4个
二、填空题
8.假期学校组织360名师生外出旅游,某客车出租公司有两种大客车可供选择:甲种客车每辆车有40个座,租金400元;乙种客车每辆车有50个座,租金480元.则租用该公司客车最少需用租金 元.
9.A城有种农机30台,B城有该农机40台,现要将这些农机全部运往C,D两乡,调运任务承包给某运输公司.已知C乡需要农机34台,D乡需要农机36台,从A城往C,D两乡运送农机的费用分别为250元/台和200元/台,从B城往C,D两乡运送农机的费用分别为150元/台和240元/台.设A城运往C乡该农机x台,运送全部农机的总费用为W元,则W关于x的函数关系式为 .
10.2019年1月18日,重庆经开区新时代文明实践“五进企业”系列活动----2019年新春游园会成功矩形,这次新春游园会的门票分为个人票和团体票两大类其中个人票设置有三种,票得种类 夜票(A) 平日普通票(B)指定日普通票(C)某社区居委会欲购买个人票100张,其中B种票的张数是A种票的3倍还多8张,设购买A种票的张数为x,C种票张数为y,则化简后y与x之间的关系式为: (不必写出x的取值范围)
11.某公司为用户提供上网服务的两种收费方式如下表:
收费标准/方式 基础费用(单位:元/月) 单价(单位:元/分)
A 0 0.1
B 20 0.05
若设用户每月上网的时间为x分钟,A,B两种收费方式的费用分别为(元)、(元),则当每月上网时间多于400分钟时,选择 种方式省钱(填“A”或“B”).
12.小静准备到甲或乙商场购买一些商品,两商场同种商品的标价相同,而各自推出不同的优惠方案:在甲商场累计购买满一定数额a元后,再购买的商品按原价的收费;在乙商场累计购买50元商品后,再购买的商品按原价的收费.若累计购物x元,当时,在甲商场需付钱数,当时,在乙商场需付钱数为.下列说法:①;②当累计购物大于50元时,选择乙商场一定优惠些;③当累计购物超过150元时,选择甲商场一定优惠些;④.其中正确的说法是 (填序号)
13.本年度某单位常有集体外出学习活动,因此准备与出租车公司签订租车协议.现有甲、乙两家出租车公司供选择.设每月行驶千米,应付给甲公司元,应付给乙公司元,、分别与之间的函数关系如图所示,若这个单位估计每月需要行驶的路程为3500千米,那么为了省钱,这个单位应租 公司.
三、解答题
14.甲、乙两商场出售相同的某种商品,每件售价均为3000元,并且多买都有一定的优惠.甲商场的优惠条件是:第一件按原价收费,其余每件优惠;乙商场的优惠条件是:每件优惠.设所买商品为()件,甲商场收费为元,乙商场收费为元.
(1)分别求出,与之间的关系式;
(2)当所买商品为5件时,选择哪家商场更优惠?请说明理由.
15.某零件制造车间有工人20名,已知每名工人每天可制造甲种零件6个或乙种零件5个,且每制造一个甲种零件可获利150元,每制造一个乙种零件可获利260元,在这20名工人中,设该车间每天安排x名工作制造甲种零件,其余工人制造乙种零件.
(1)请写出此车间每天所获利润y(元)与x(人)之间的函数关系式;
(2)若只考虑利润问题,要使每天所获利润不低于24000元,你认为至多要派多少名工人制造甲种零件才合适?
16.某公司要印制大运会这传材料,甲印刷厂提出:每份材料收1元印制费,另收元制版费:乙印刷厂提出:每份材料收3元印制费,不收制版费.
(1)分别写出两印刷厂的收费y(元)与印制数量x(份)之间的关系式;
请你用自己的方法,回答下列问题:
(2)印刷份宣传材料时,选择哪家印刷厂比较合算?
(3)该公司拟拿出元用于印制宣传材料,找哪家印刷厂印制宣传材料能多一些?
17.随着生活水平的日益提高,人们的健康意识逐渐增强,越来越多的人把健身作为一种时尚的生活方式,某商家抓住机遇推出促销活动,向客户提供了两种优惠方案:
方案一:买一件运动外套送一件卫衣;
方案二:运动外套和卫衣均在定价的基础上打8折.
运动外套每件定价300元,卫衣每件定价100元.在开展促销活动期间,某俱乐部要到该商场购买运动外套100件,卫衣件().
(1)方案一需付款:______元,方案二需付款:______元;
(2)当时,请计算并比较这两种方案哪种更划算;
(3)当时,如果两种方案可以组合使用,你能帮助俱乐部设计一种最省钱的方案吗?请直接写出你的方案.
18.某游泳馆夏季推出两种游泳付费方式.方式一:先购买会员证,每张会员证100元,只限本人当年使用,凭证游泳每次再付费15元;方式二:不购买会员证,每次游泳付费20元.设小明计划今年夏季游泳次数为x次(x为正整数).
(1)根据题意,将表格填写完整.
游泳次数 10 15 20 …
采用方式一付费(元) 250 325 __ …
采用方式二付费(元) 200 __ 400 …
(2)设方式一的总费用为元,方式二的总费用为元,分别用x表示和;
(3)通过计算说明,当和时,分别应选择哪种付费方式较合算?
19.某超市鸡蛋供应紧张,需每天从外地调运鸡蛋千克.超市决定从甲、乙两大型养殖场调运鸡蛋,已知甲养殖场每天最多可调出千克,乙养殖场每天最多可调出千克,从甲、乙两养殖场调运鸡蛋到该超市的路程和运费如表:
到超市的路程(千米) 运费(元/千克·千米)
甲养殖场
乙养殖场
设从甲养殖场调运鸡蛋千克,总运费为元.
(1)从甲养殖场调运鸡蛋的运费,用代数式表示为______,从乙养殖场需要调运鸡蛋的数量,用代数式表示为______;
(2)试写出与的函数关系式;
(3)请求出自变量取值范围,说明怎样安排调运方案才能使每天的总运费最少?
20.为响应政府低碳生活,绿色出行的号召,某公交公司决定购买一批节能环保的新能源公交车,计划购买型和型两种公交车,其中每辆的价格、年载客量如表:
型 型
价格(万元/辆)
年载客量(万人/年) 60 100
若购买型公交车1辆,型公交车2辆,共需400万元;若购买型公交车2辆,型公交车1辆,共需350万元.
(1)求,的值;
(2)计划购买型和型两种公交车共10辆,如果该公司购买型和型公交车的总费用不超过1200万元,且确保这10辆公交车在该线路的年均载客总和不少于640万人次,问有几种购买方案
(3)在(2)的条件下,请用一次函数的性质说明哪种方案使得购车总费用最少 最少费用是多少万元
参考答案
1.解:设小明行驶里程是x千米,需要花费y元,
A方案:一共需要花费:,
B方案∶ 一共需要花费:,
若选择A方案,,解得:,
若选择B方案,得,
由于,则选择B方案是最优租车方案,行驶里程为800米,
故选:C.
2.解:依题意设旅行社全票价为x元,三人旅行实际收费为y元.可知东方旅行社三人旅行实际收费为:y=2x+70%x=2.7x(元)而光明旅行社三人旅行实际收费为:=2.7x.可知两家旅行社实际收费相同.
3.解:设租用甲客车x辆,租车总费用y元,由每辆客车上至少要有1名教师可知客车总数不能大于7辆,
要保证240名师生有车坐,客车总数不能小于,客车总数不能小于6,
∴客车总数为6,,
由题意可得,,
整理可得,
由题意,,
解得,
∵,
∴,
∵中,,y随x的增大而增大,
∴x取最小值时,即,y有最小值,
即当租甲种车4辆,租乙种车2辆,费用最少,
故选:A.
4.解:设直线AB的解析式为,
将(2,38)、(4,70)代入得,,
解得:,
当时,,
即萌萌一次购买6千克这种葡萄需要元;
她分三次购买每次购2千克这种葡萄需要(元),
∴(元),
萌萌一次购买6千克这种葡萄比她分三次购买每次购2千克这种葡萄可节省12元.
故选:B.
5.解:在方案一中,设OA表示的解析式为,且
解得,
表示的解析式为:;
设表示的解析式为,
又,
解得,,
表示的解析式为:;
方案二的解析式为:;
当时,
故的图象与的图象无交点,
当时,,
所以,当时,两种方案购票总价相同.
故选:D.
6.解:利用图象,当游泳次数大于10次时,
在上面,即>,
∴当游泳次数为30次时,选择乙种方式省钱.
故选:B.
7.解:依题意得
A:(1)当0≤x≤120,yA=30,
(2)当x>120,yA=30+(x-120)×[(50-30)÷(170-120)]=0.4x-18;
B:(1)当0≤x<200,yB=50,
当x>200,yB=50+[(70-50)÷(250-200)](x-200)=0.4x-30,
所以当x≤120时,A方案比B方案便宜20元,故(1)正确;
当x≥200时,B方案比A方案便宜12元,故(2)正确;
当y=60时,A:60=0.4x-18,∴x=195,
B:60=0.4x-30,∴x=225,故(3)正确;
当A方案与B方案的费用相等,通话时间为170分钟,故(4)正确;
故选:D.
8.解:若只租甲种客车需要辆.若只租乙种客车需要8辆,因而两种客车用共租8辆.
设甲车有x辆,乙车有辆,则,
解得:,
整数解为1、2、3、4.
设汽车的租金为,
则:,即,
的值随的增大而减小,因而当时,最小.
故取,的最小值是3520元.
9.解:由题意得:因为A城运往C乡x台农机,则A城运往D乡(30﹣x)台农机,B城运往C乡(34﹣x)台农机,B城运往D乡[40﹣(34﹣x)]台农机
W=250x+200(30﹣x)+150(34﹣x)+240[40﹣(34﹣x)]
=140x+12540,
故答案为:W=140x+12540.
10.解:由题可知,,
∴.
故答案为.
11.解:由题意可知:=0.1x,=20+0.05x,
当=时,由0.1x=20+0.05x得:x=400,两种收费方式一样省钱;
当>时,由0.1x>20+0.05x得:x>400,B种方式省钱;
当<时,由0.1x<20+0.05x得:x<400,A种方式省钱,
∴当每月上网时间多于400分钟时,选择B种方式省钱,
故答案为:B.
12.解:①、,正确,符合题意;
②、当累计购物大于50时上没封顶,选择乙商场一定优惠显然不对,不符合题意;
③、当时,即,解之得.所以当累计购物超150元时,选择甲商场一定优惠些,符合题意;
④、根据题意,所以,符合题意;
故答案为:①③④.
13.解:根据图象可知当x>1500时,,此时甲省钱.
∵x=3500>1500,此时,
∴此时甲省钱.
故答案为:甲.
14.(1)解:由题意可得,
.
(2)当时,,
,
∵,
∴所买商品为5件时,应选择乙商场更优惠.
15.(1)解:设该车间每天安排x名工作制造甲种零件,则安排人制造乙种零件,
根据题意:
即;
(2)解:根据题意:令
解得:,
在中,
∵,
∴y的值随x的值的增大而减少,
∴要使,需,
答:至多要派5名工人制造甲种零件才合适.
16.解:(1)由题意得:甲厂收费y(元)与印制数量x(份)之间的关系式为,乙厂收费y(元)与印制数量x(份)之间的关系式为;
解:(2)当时,甲厂:(元);乙厂:(元).
∵
乙厂比较合算;
解:(3)当时,
甲厂:,解得(份);
乙厂:,解得(份),
∵.
甲厂印制宣传材料多一些.
17.(1)解:方案一∶ 购买运动外套100件,送100件卫衣,则还需购买件卫衣,
方案一需付款元;
方案二∶ 购买运动外套100件,卫衣x件,均打8折,
方案二 需付款元.
(2)当时,
方案一需付款:(元)
方案二需付款:(元)
(3)设购买a件运动外套使用方案一,则购买件运动外套使用方案二,
购买a件卫衣使用方案一,购买件卫衣使用方案二,
设总费用为w元,
则,
∵,费用w随着a的增大而减小.
∴当时,w取的最小值46000,即总费用最小,
∴最省钱的方案:按照方案一购买100件运动外套再按照方案二购买200件卫衣.
18.(1)解:当时,方式一:元,
当时,方式二:元;
(2)解:由题意,方式一的总费用:,
方式二的总费用:;
(3)解:当时,方式一:,
方式二:,
,方式二更划算;
当时,方式一:,
方式二:,
,方式一更划算.
综上所示,当时,选择方式二,当时,选择方式一.
19.解:(1)从甲养殖场调运鸡蛋千克,则从乙养殖场调运鸡蛋千克,
则从甲养殖场调运鸡蛋的运费为元,
故答案为:元,千克;
(2)由题意得,
与的函数关系式为;
(3)由题意得, ,,
,
由()知,
,
随的增大而增大,
当时,取得最小值,此时,
此时,
答:当从甲养殖场调运斤鸡蛋,从乙养殖场调运斤鸡蛋时,每天的总运费最省,总运费最低是元.
20.(1)解:依题意得:,解得:,
答:的值为100,的值为150;
(2)解:设购买型公交车辆,则购买型公交车辆,
依题意得:
解得:
又为整数
有4购买方案;
(3)解:设购车总费用为万元,
则,(且为整数)
,
随的增大而减小
当时,最小,最小值为(元),
购车总费用最少的方案是购买型公交车9辆,购买型公交车1辆,购车总费用为1050万元.
