19.3课题学习-选择方案-—次函数的实际应用-几何问题 专题提升训练(含解析)2023-2024学年人教版八年级数学下册
文档属性
| 名称 | 19.3课题学习-选择方案-—次函数的实际应用-几何问题 专题提升训练(含解析)2023-2024学年人教版八年级数学下册 |  | |
| 格式 | docx | ||
| 文件大小 | 612.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-04-17 21:58:38 | ||
图片预览



文档简介
2023-2024学年人教版八年级数学下册《19.3课题学习-选择方案-—次函数的实际应用-几何问题》专题提升训练(附答案)
一、单选题
1.已知等腰三角形的周长为,则底边长与腰长的函数关系式是( )
A. B.
C. D.
2.直线与x轴交于点A,与y轴交于点B,点O为坐标原点,若,则( ).
A.8 B. C. D.
3.直线与x轴交于点A,以为斜边在x轴上方做等腰直角三角形,其中,将沿着x轴方向向右平移,当点B落在直线上时,则平移的距离是( )
A.2 B. C.6 D.10
4.如图,直线交轴,轴于点,,点在第一象限内,且纵坐标为1.若点关于直线的对称点恰好落在轴的正半轴上,则点的横坐标为( )
A. B. C. D.
5.如图,在直角坐标系中,点的坐标分别为和,点是轴上一个动点,当的周长最小时点的坐标为( )
A. B. C. D.
6.如图,已知点,,点为轴上一点当最大值时,点的坐标为( )
A. B. C. D.
7.如图,已知直线与轴、轴分别交于点和点,是线段上一点,若将沿折叠,点恰好落在x轴上的点处,则直线所对应的函数表达式是( )
A. B.
C. D.
二、填空题
8.若第四象限内的一点P在一次函数的图像上,且点P到y轴的距离等于3,则点P的坐标是 .
9.已知直线:与x轴交于点A,与y轴交于点B,点C是直线上的一点,且满足.则点C的坐标为 .
10.已知直线与x轴交于点A,与y轴交于点B,点C是y轴上一动点,是以为腰的等腰三角形,则满足条件的点C的坐标为 .
11.如图,在平面直角坐标系中,已知点,,点C在直线上.若,则点C的坐标为 .
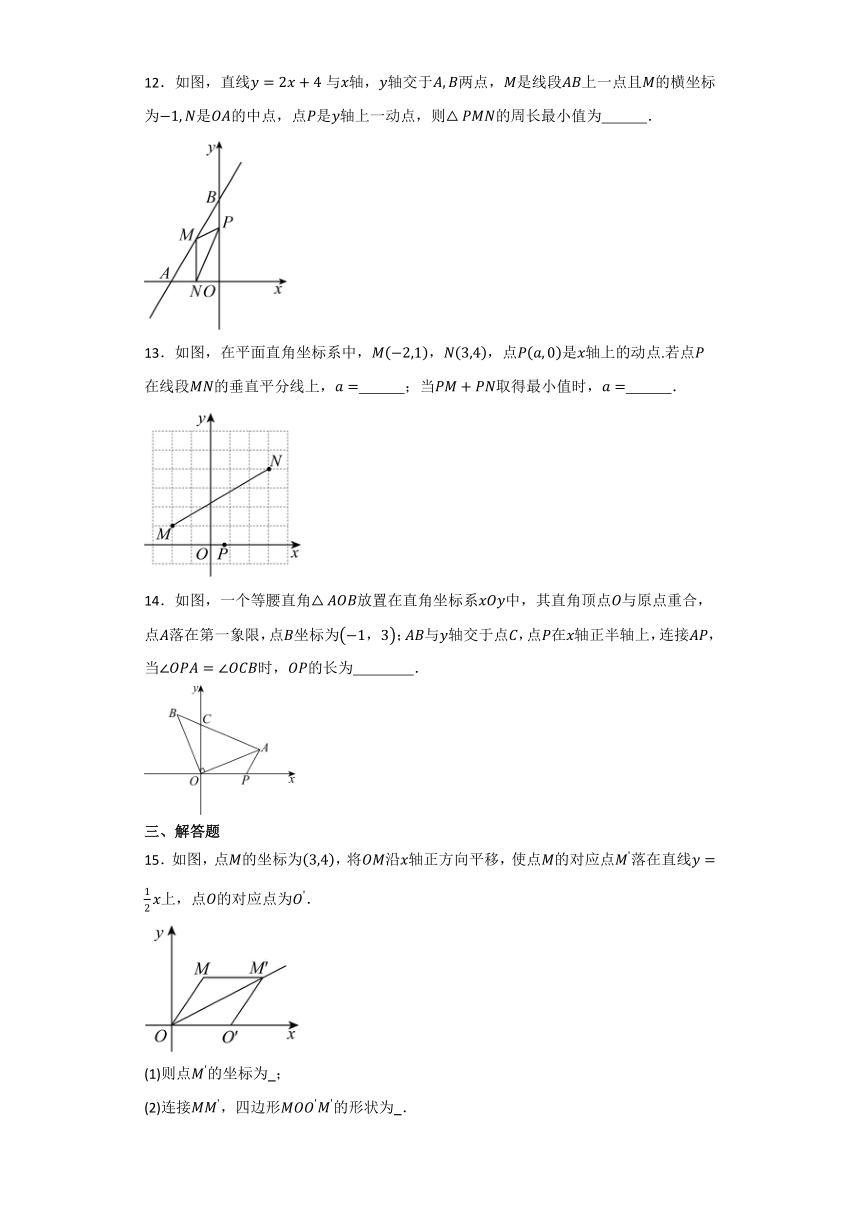
12.如图,直线与轴,轴交于两点,是线段上一点且的横坐标为是的中点,点是轴上一动点,则的周长最小值为 .
13.如图,在平面直角坐标系中,,,点是轴上的动点.若点在线段的垂直平分线上, ;当取得最小值时, .
14.如图,一个等腰直角放置在直角坐标系中,其直角顶点与原点重合,点落在第一象限,点坐标为;与轴交于点,点在轴正半轴上,连接,当时,的长为 .
三、解答题
15.如图,点的坐标为,将沿轴正方向平移,使点的对应点落在直线上,点的对应点为.
(1)则点的坐标为 ;
(2)连接,四边形的形状为 .
16.如图所示,在同一个坐标系中一次函数和的图象,分别与轴交于点、,两直线交于点.已知点坐标为,点坐标为,观察图象并回答下列问题:
(1)关于x的方程的解是___;关于的不等式的解集是______.
(2)直接写出关于x的不等式组解集是______.
(3)若点坐标为,
①关于的不等式的解集是______;
②的面积为______.
③在轴上找点,使得的值最大,则点坐标为______.
17.如图,在平面直角坐标系中,直线与x轴、y轴分别交A、B两点,与直线y相交于点.
(1)求m和b的值;
(2)若直线与x轴相交于点D,动点P从点D开始,以每秒1个单位的速度向x轴负方向运动,设点P的运动时间为t秒.
①若点P在线段上,且的面积为10,求t的值;
②是否存在t的值,使为等腰三角形?若存在,求出t的值;若不存在,请说明理由.
18.如图,在平面直角坐标系中,矩形的顶点A在轴的正半轴上,点在轴的正半轴上,线段的长分别是且满足,点是线段上一点,将沿直线翻折,点落在矩形的对角线上的点处.
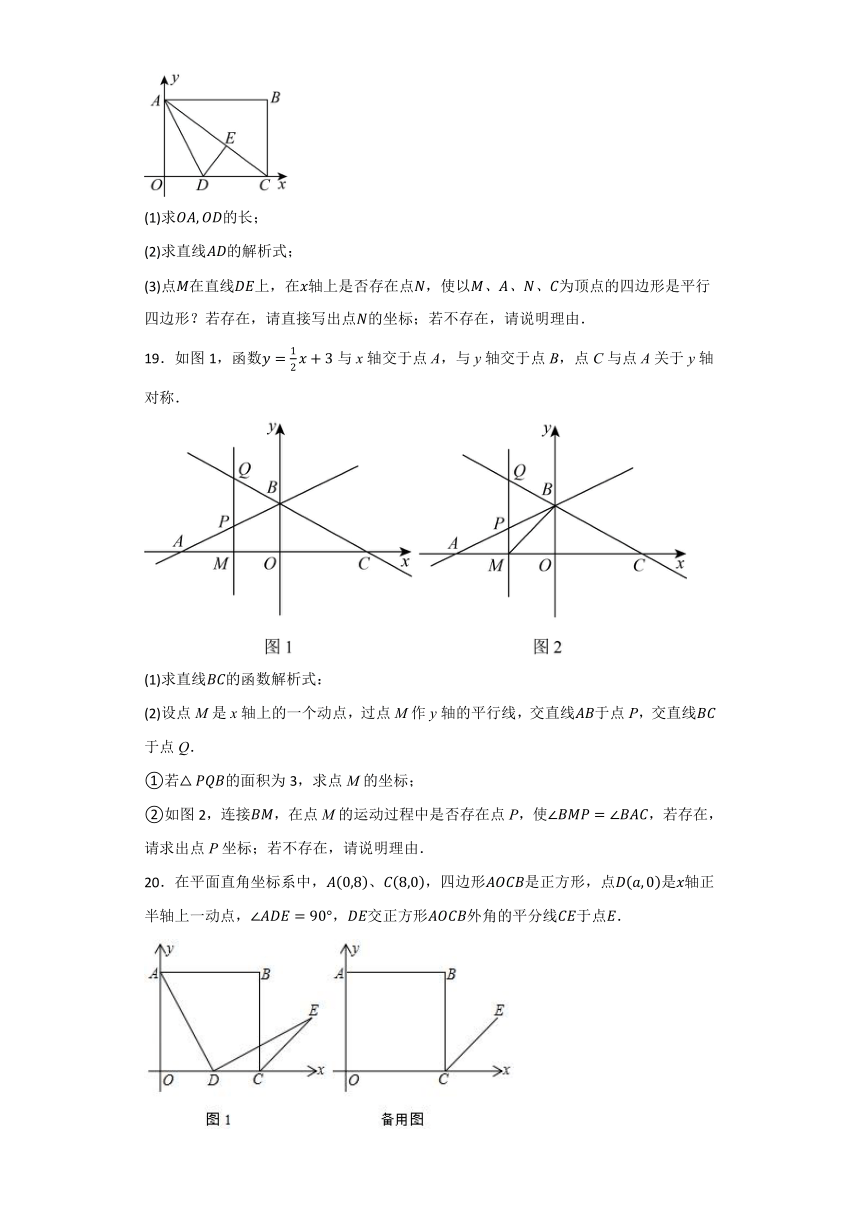
(1)求的长;
(2)求直线的解析式;
(3)点在直线上,在轴上是否存在点,使以为顶点的四边形是平行四边形?若存在,请直接写出点的坐标;若不存在,请说明理由.
19.如图1,函数与x轴交于点A,与y轴交于点B,点C与点A关于y轴对称.
(1)求直线的函数解析式:
(2)设点M是x轴上的一个动点,过点M作y轴的平行线,交直线于点P,交直线于点Q.
①若的面积为3,求点M的坐标;
②如图2,连接,在点M的运动过程中是否存在点P,使,若存在,请求出点P坐标;若不存在,请说明理由.
20.在平面直角坐标系中,、,四边形是正方形,点是轴正半轴上一动点,,交正方形外角的平分线于点.
(1)如图1,当点是的中点时,求证:;
(2)点在轴正半轴上运动,点在轴上.若四边形为菱形,求直线的解析式.
(3)连,点是的中点,当点在轴正半轴上运动时,点随之而运动,点到的距离是否为定值?若为定值,求出这个值;若不是定值,请说明理由.
参考答案
1.解:
,
,
即,
,
又两边之和大于第三边,即,
解得:,
故底边长与腰长的函数关系式是:.
故选:A.
2.解: ∵一次函数的图象与x轴交于点A,与y轴交于点B,
∵的面积为4,
即
解得:
故选:C.
3.解:在,当时,,
解得:,
∴,即,
过作于,
是以为斜边的等腰直角三角形,
,即点的坐标是,
设平移的距离为,
则点的对称点的坐标为,
代入得:,
解得:,即平移的距离是6,
故选:C.
4.解:直线交轴,轴于点,,
,,即,,
连接,,,
点在第一象限内,且纵坐标为1,
轴,
,
点关于直线的对称点恰好落在轴的正半轴上,
,
,
,
设,则,
,
,即,解得,
点的横坐标为.
故选:C.
5.解:如下图,作点关于轴的对称点,作直线,交轴于点,此时的周长最小,
∵,
∴,
设直线的解析式为,
将点,代入,
可得,解得,,
∴直线的解析式为,
令,可有,,
解得,
∴.
故选:B.
6.解:作关于轴对称点,连接并延长交轴于点,
,
的坐标为,
设直线的解析式为:,
,
解得:,
直线的解析式为:,
当时,,
点的坐标为:,,
当,,不共线时,根据三角形三边的关系可得:,
此时取得最大值.
故选:B.
7.解:在中,当时,,当时,,解得,
,,
,,
,
由折叠的性质可得:,,
,
设,
,则,
,
,
解得:,
,
设直线的解析式为,
将,代入解析式得,
解得:,
直线的解析式为,
故选:B.
8.解:∵点P到y轴的距离等于3,
∴,
∵点P在第四象限内,
∴,
∴,
∴点P的坐标是,
故答案为:.
9.解:在中,当时,,
∴,
∴,
∵,
∴,
∴,
∴,
在中,当时,,当时,,
∴点C的坐标为或,
故答案为;或.
10.解:如图:
当时,
∴点B的坐标为,
∴;
当时,
解得:,
∴点A的坐标为,
∴.
在中,,,,
当为腰时,,
∴点C的坐标为;
当为腰时,,
又∵点B的坐标为,
∴点C的坐标为或.
综上所述,满足条件的点C的坐标为或或.
故答案为:或或.
11.解:过点B作直线轴,过点B作交于点D,过点A,D作直线l的垂线,垂足分别为E,F,如图所示:
∵点,
∴,
在中,由勾股定理得:,
在中,,
由勾股定理得:,
∵,
∴为等腰直角三角形,
∴,
∵直线l,直线l,
∴,
∵,
∴,
在和中,
,
∴,
∴点D的横坐标为,设点D的纵坐标y,
由两点间的距离公式得:,
∴,
解得:,
∴点D的坐标为或,
①当点时,由两点间的距离公式得:,
∴点,符合题意,
②当时,由两点间的距离公式得:,
∴点不符合题意,舍去,
设直线的表达式为,
将点,点代入得:
,解得:,
∴直线的表达式为:,
解方程组,得:,
∴点C的坐标为.
故答案为:.
12.解:在中,令,则,令,则,
∴,,
∵N是的中点,
∴,
∴;
作点关于轴对称的点,连接,则的坐标为,
,
∴,
∵的周长,
∴当M、P、Q三点共线时最小,即此时的周长最小,最小值为,
∵,,
∴
∴的周长的最小值为.
故答案为:.
13.解:当点P在线段的垂直平分线上时:有,
∴,
解得,
当取得最小值时:
取关于x轴的对称点,连接交x轴于点P,如图,
设直线的解析式为:
将,代入,得
,
解得,
∴直线的解析式为:,
当时,,
解得,
∴.
故答案为:2,.
14.解:如图:过点B作轴,过A作轴,
则,
∵等腰直三角形,
∴,
∴,
∴,
∴,
∵点B的坐标为,
∴,
∴点A的坐标为,
又∵,
∴,
∴,
设直线的解析式为
把点A的坐标为和点B的坐标为分别代入,
得
解得
由点的坐标可得直线的解析式为,
当时,,
∴,
∴,
∴.
故答案为:.
15.解:(1)把代入
得,
点坐标为,
故答案为:;
(2)四边形为菱形.
理由如下:过点作轴于点,
由平移得,,
四边形为平行四边形,
点的坐标为,
点的坐标为,点坐标为,
平行四边形为菱形,
故答案为:菱形.
16.(1)解:一次函数和的图象,分别与轴交于点、,点坐标为,点坐标为,
关于的方程的解是,关于的不等式的解集为,
(2)根据图象可以得到关于的不等式组的解集;
(3)①∵点,
结合图象可知,不等式的解集是;
②,,
;
③,记交轴于点,
此时,此时最大,
设直线为,
∴,解得,
直线为,
令,则,
,
17.解:(1)在中,当时,;
当时,;
∴;
∵点C在直线上,
∴,
又∵点也在直线上,
∴,
解得:;
(2)①在中,当时,,
∴,
∴,
∵,
∴,
∴;
设,则,过C作于E,如图1所示:
则,
∵的面积为10,
∴,
解得:;
②存在,理由如下:
过C作于E,如图1所示:
则,
∴,
∴;
a、当时,,
∴,
∴;
b、当时,如图2所示:
则,
∴,,
∴,或;
c、当时,如图3所示:
设,则,,
∴,
解得:,
∴P与E重合,,
∴,
∴;
t的值为4或或或8.
18.(1)解:∵线段的长分别是且满足,
∴,,
∴,;
设,
由翻折的性质可得:,,,
而,
∴,
在中,由勾股定理可得:,
即,
解得:,
∴,
(2)由(1)点D的坐标为,
设的解析式为:,
把,代入解析式可得: ,
解得: ,
∴直线的解析式为:;
(3)过E作,在中,,
即,
解得:,
在中, ,
∴点E的坐标为,
设直线的解析式为:,
把,代入解析式可得: ,
解得: ,
所以的解析式为:,
把代入的解析式,可得:,
此时,
即,
当以M、A、N、C为顶点的四边形是平行四边形且为边时,
∴,
∴,,
∴点N的坐标为或.
如图,当为平行四边形的对角线时,
设,,而,,
∴,
解得:,
∴;
综上:的坐标为或或.
19.(1)解:对于,
当时,,
当时,,
解得:,
∴点,
∵点C与点A关于y轴对称,
∴点,
设直线的解析式为,
∴,解得:,
∴直线的解析式为;
(2)解:①设,则点,
如图,过点B作于点D,
则,
∵的面积为3,
∴,
解得:,
∴点M的坐标为或;
②如图,当点M在y轴的左侧时,
∵点C与点A关于y轴对称,
∴,
∴,
∵,
∴,
∵,
∴,
∴,
∴,
设,则,
∴,
∴,
解得:,
∴,
当点M在y轴的右侧时,
同理可得,
综上所述,点P的坐标为或.
20.(1)证明:如图1中,取的中点,连接.
为正方形的外角平分线,
∴,
∴,
∵分别为的中点,
∴,
∴是等腰直角三角形,
∴,
∴,
∴,
∵,
∴,
∴,
∴.
(2)解:如图2中,作交作于,由四边形是正方形,可证,
,
∴,
由(1)可知,
∴,
∴四边形是平行四边形,当点在边上时,点在上,,
∴四边形不可能是菱形,
∴点在点的右侧,
如图3中,
∵四边形是菱形,
∴,
∵,,
∴,
∴,
设直线的解析式为,则有,
解得,
∴直线的解析式为.
(3)解:如图4或5,连接.
∵,
∴,
∵是中点,
∴,
∴点在的垂直平分线上,
∵垂直平分,
∴点在直线上,
∵,
∴,
∴点到的距离为定值且等于平行线之间的距离,
∴点到的距离.
一、单选题
1.已知等腰三角形的周长为,则底边长与腰长的函数关系式是( )
A. B.
C. D.
2.直线与x轴交于点A,与y轴交于点B,点O为坐标原点,若,则( ).
A.8 B. C. D.
3.直线与x轴交于点A,以为斜边在x轴上方做等腰直角三角形,其中,将沿着x轴方向向右平移,当点B落在直线上时,则平移的距离是( )
A.2 B. C.6 D.10
4.如图,直线交轴,轴于点,,点在第一象限内,且纵坐标为1.若点关于直线的对称点恰好落在轴的正半轴上,则点的横坐标为( )
A. B. C. D.
5.如图,在直角坐标系中,点的坐标分别为和,点是轴上一个动点,当的周长最小时点的坐标为( )
A. B. C. D.
6.如图,已知点,,点为轴上一点当最大值时,点的坐标为( )
A. B. C. D.
7.如图,已知直线与轴、轴分别交于点和点,是线段上一点,若将沿折叠,点恰好落在x轴上的点处,则直线所对应的函数表达式是( )
A. B.
C. D.
二、填空题
8.若第四象限内的一点P在一次函数的图像上,且点P到y轴的距离等于3,则点P的坐标是 .
9.已知直线:与x轴交于点A,与y轴交于点B,点C是直线上的一点,且满足.则点C的坐标为 .
10.已知直线与x轴交于点A,与y轴交于点B,点C是y轴上一动点,是以为腰的等腰三角形,则满足条件的点C的坐标为 .
11.如图,在平面直角坐标系中,已知点,,点C在直线上.若,则点C的坐标为 .
12.如图,直线与轴,轴交于两点,是线段上一点且的横坐标为是的中点,点是轴上一动点,则的周长最小值为 .
13.如图,在平面直角坐标系中,,,点是轴上的动点.若点在线段的垂直平分线上, ;当取得最小值时, .
14.如图,一个等腰直角放置在直角坐标系中,其直角顶点与原点重合,点落在第一象限,点坐标为;与轴交于点,点在轴正半轴上,连接,当时,的长为 .
三、解答题
15.如图,点的坐标为,将沿轴正方向平移,使点的对应点落在直线上,点的对应点为.
(1)则点的坐标为 ;
(2)连接,四边形的形状为 .
16.如图所示,在同一个坐标系中一次函数和的图象,分别与轴交于点、,两直线交于点.已知点坐标为,点坐标为,观察图象并回答下列问题:
(1)关于x的方程的解是___;关于的不等式的解集是______.
(2)直接写出关于x的不等式组解集是______.
(3)若点坐标为,
①关于的不等式的解集是______;
②的面积为______.
③在轴上找点,使得的值最大,则点坐标为______.
17.如图,在平面直角坐标系中,直线与x轴、y轴分别交A、B两点,与直线y相交于点.
(1)求m和b的值;
(2)若直线与x轴相交于点D,动点P从点D开始,以每秒1个单位的速度向x轴负方向运动,设点P的运动时间为t秒.
①若点P在线段上,且的面积为10,求t的值;
②是否存在t的值,使为等腰三角形?若存在,求出t的值;若不存在,请说明理由.
18.如图,在平面直角坐标系中,矩形的顶点A在轴的正半轴上,点在轴的正半轴上,线段的长分别是且满足,点是线段上一点,将沿直线翻折,点落在矩形的对角线上的点处.
(1)求的长;
(2)求直线的解析式;
(3)点在直线上,在轴上是否存在点,使以为顶点的四边形是平行四边形?若存在,请直接写出点的坐标;若不存在,请说明理由.
19.如图1,函数与x轴交于点A,与y轴交于点B,点C与点A关于y轴对称.
(1)求直线的函数解析式:
(2)设点M是x轴上的一个动点,过点M作y轴的平行线,交直线于点P,交直线于点Q.
①若的面积为3,求点M的坐标;
②如图2,连接,在点M的运动过程中是否存在点P,使,若存在,请求出点P坐标;若不存在,请说明理由.
20.在平面直角坐标系中,、,四边形是正方形,点是轴正半轴上一动点,,交正方形外角的平分线于点.
(1)如图1,当点是的中点时,求证:;
(2)点在轴正半轴上运动,点在轴上.若四边形为菱形,求直线的解析式.
(3)连,点是的中点,当点在轴正半轴上运动时,点随之而运动,点到的距离是否为定值?若为定值,求出这个值;若不是定值,请说明理由.
参考答案
1.解:
,
,
即,
,
又两边之和大于第三边,即,
解得:,
故底边长与腰长的函数关系式是:.
故选:A.
2.解: ∵一次函数的图象与x轴交于点A,与y轴交于点B,
∵的面积为4,
即
解得:
故选:C.
3.解:在,当时,,
解得:,
∴,即,
过作于,
是以为斜边的等腰直角三角形,
,即点的坐标是,
设平移的距离为,
则点的对称点的坐标为,
代入得:,
解得:,即平移的距离是6,
故选:C.
4.解:直线交轴,轴于点,,
,,即,,
连接,,,
点在第一象限内,且纵坐标为1,
轴,
,
点关于直线的对称点恰好落在轴的正半轴上,
,
,
,
设,则,
,
,即,解得,
点的横坐标为.
故选:C.
5.解:如下图,作点关于轴的对称点,作直线,交轴于点,此时的周长最小,
∵,
∴,
设直线的解析式为,
将点,代入,
可得,解得,,
∴直线的解析式为,
令,可有,,
解得,
∴.
故选:B.
6.解:作关于轴对称点,连接并延长交轴于点,
,
的坐标为,
设直线的解析式为:,
,
解得:,
直线的解析式为:,
当时,,
点的坐标为:,,
当,,不共线时,根据三角形三边的关系可得:,
此时取得最大值.
故选:B.
7.解:在中,当时,,当时,,解得,
,,
,,
,
由折叠的性质可得:,,
,
设,
,则,
,
,
解得:,
,
设直线的解析式为,
将,代入解析式得,
解得:,
直线的解析式为,
故选:B.
8.解:∵点P到y轴的距离等于3,
∴,
∵点P在第四象限内,
∴,
∴,
∴点P的坐标是,
故答案为:.
9.解:在中,当时,,
∴,
∴,
∵,
∴,
∴,
∴,
在中,当时,,当时,,
∴点C的坐标为或,
故答案为;或.
10.解:如图:
当时,
∴点B的坐标为,
∴;
当时,
解得:,
∴点A的坐标为,
∴.
在中,,,,
当为腰时,,
∴点C的坐标为;
当为腰时,,
又∵点B的坐标为,
∴点C的坐标为或.
综上所述,满足条件的点C的坐标为或或.
故答案为:或或.
11.解:过点B作直线轴,过点B作交于点D,过点A,D作直线l的垂线,垂足分别为E,F,如图所示:
∵点,
∴,
在中,由勾股定理得:,
在中,,
由勾股定理得:,
∵,
∴为等腰直角三角形,
∴,
∵直线l,直线l,
∴,
∵,
∴,
在和中,
,
∴,
∴点D的横坐标为,设点D的纵坐标y,
由两点间的距离公式得:,
∴,
解得:,
∴点D的坐标为或,
①当点时,由两点间的距离公式得:,
∴点,符合题意,
②当时,由两点间的距离公式得:,
∴点不符合题意,舍去,
设直线的表达式为,
将点,点代入得:
,解得:,
∴直线的表达式为:,
解方程组,得:,
∴点C的坐标为.
故答案为:.
12.解:在中,令,则,令,则,
∴,,
∵N是的中点,
∴,
∴;
作点关于轴对称的点,连接,则的坐标为,
,
∴,
∵的周长,
∴当M、P、Q三点共线时最小,即此时的周长最小,最小值为,
∵,,
∴
∴的周长的最小值为.
故答案为:.
13.解:当点P在线段的垂直平分线上时:有,
∴,
解得,
当取得最小值时:
取关于x轴的对称点,连接交x轴于点P,如图,
设直线的解析式为:
将,代入,得
,
解得,
∴直线的解析式为:,
当时,,
解得,
∴.
故答案为:2,.
14.解:如图:过点B作轴,过A作轴,
则,
∵等腰直三角形,
∴,
∴,
∴,
∴,
∵点B的坐标为,
∴,
∴点A的坐标为,
又∵,
∴,
∴,
设直线的解析式为
把点A的坐标为和点B的坐标为分别代入,
得
解得
由点的坐标可得直线的解析式为,
当时,,
∴,
∴,
∴.
故答案为:.
15.解:(1)把代入
得,
点坐标为,
故答案为:;
(2)四边形为菱形.
理由如下:过点作轴于点,
由平移得,,
四边形为平行四边形,
点的坐标为,
点的坐标为,点坐标为,
平行四边形为菱形,
故答案为:菱形.
16.(1)解:一次函数和的图象,分别与轴交于点、,点坐标为,点坐标为,
关于的方程的解是,关于的不等式的解集为,
(2)根据图象可以得到关于的不等式组的解集;
(3)①∵点,
结合图象可知,不等式的解集是;
②,,
;
③,记交轴于点,
此时,此时最大,
设直线为,
∴,解得,
直线为,
令,则,
,
17.解:(1)在中,当时,;
当时,;
∴;
∵点C在直线上,
∴,
又∵点也在直线上,
∴,
解得:;
(2)①在中,当时,,
∴,
∴,
∵,
∴,
∴;
设,则,过C作于E,如图1所示:
则,
∵的面积为10,
∴,
解得:;
②存在,理由如下:
过C作于E,如图1所示:
则,
∴,
∴;
a、当时,,
∴,
∴;
b、当时,如图2所示:
则,
∴,,
∴,或;
c、当时,如图3所示:
设,则,,
∴,
解得:,
∴P与E重合,,
∴,
∴;
t的值为4或或或8.
18.(1)解:∵线段的长分别是且满足,
∴,,
∴,;
设,
由翻折的性质可得:,,,
而,
∴,
在中,由勾股定理可得:,
即,
解得:,
∴,
(2)由(1)点D的坐标为,
设的解析式为:,
把,代入解析式可得: ,
解得: ,
∴直线的解析式为:;
(3)过E作,在中,,
即,
解得:,
在中, ,
∴点E的坐标为,
设直线的解析式为:,
把,代入解析式可得: ,
解得: ,
所以的解析式为:,
把代入的解析式,可得:,
此时,
即,
当以M、A、N、C为顶点的四边形是平行四边形且为边时,
∴,
∴,,
∴点N的坐标为或.
如图,当为平行四边形的对角线时,
设,,而,,
∴,
解得:,
∴;
综上:的坐标为或或.
19.(1)解:对于,
当时,,
当时,,
解得:,
∴点,
∵点C与点A关于y轴对称,
∴点,
设直线的解析式为,
∴,解得:,
∴直线的解析式为;
(2)解:①设,则点,
如图,过点B作于点D,
则,
∵的面积为3,
∴,
解得:,
∴点M的坐标为或;
②如图,当点M在y轴的左侧时,
∵点C与点A关于y轴对称,
∴,
∴,
∵,
∴,
∵,
∴,
∴,
∴,
设,则,
∴,
∴,
解得:,
∴,
当点M在y轴的右侧时,
同理可得,
综上所述,点P的坐标为或.
20.(1)证明:如图1中,取的中点,连接.
为正方形的外角平分线,
∴,
∴,
∵分别为的中点,
∴,
∴是等腰直角三角形,
∴,
∴,
∴,
∵,
∴,
∴,
∴.
(2)解:如图2中,作交作于,由四边形是正方形,可证,
,
∴,
由(1)可知,
∴,
∴四边形是平行四边形,当点在边上时,点在上,,
∴四边形不可能是菱形,
∴点在点的右侧,
如图3中,
∵四边形是菱形,
∴,
∵,,
∴,
∴,
设直线的解析式为,则有,
解得,
∴直线的解析式为.
(3)解:如图4或5,连接.
∵,
∴,
∵是中点,
∴,
∴点在的垂直平分线上,
∵垂直平分,
∴点在直线上,
∵,
∴,
∴点到的距离为定值且等于平行线之间的距离,
∴点到的距离.
