19.3课题学习-选择方案-—次函数的实际应用-销售利润问题 专题提升训练(含解析)2023—2024学年人教版八年级数学下册
文档属性
| 名称 | 19.3课题学习-选择方案-—次函数的实际应用-销售利润问题 专题提升训练(含解析)2023—2024学年人教版八年级数学下册 |  | |
| 格式 | docx | ||
| 文件大小 | 163.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-04-18 08:06:04 | ||
图片预览



文档简介
2023-2024学年人教版八年级数学下册《19.3课题学习-选择方案-—次函数的实际应用-销售利润问题》专题提升训练(附答案)
一、单选题
1.元旦期间,某商场搞优惠促销活动,其活动内容是:“凡在本商场一次性购物超过100元者,超过100元的部分按9折优惠”.在此活动中,李明到该商场为单位一次性购买单价为60元的办公用品x(x>2)件,则应付款y(元)与商品件数x(件)之间的关系式是( )
A.y=54x B.y=54x+10
C.y=54x-90 D.y=54x+45
2.某公司市场营销部的个人收入(元)与其每月的销售量(万件)成一次函数关系,其图象如图所示,营销人员没有销售时(最低工资)的收入是( )
A.2000元 B.3000元 C.3500元 D.4000元
3.某电脑公司经营A,B两种台式电脑,分析过去的销售记录可以知道:每台A型电脑可盈利200元,每台B型电脑可盈利300元;在同一时期内,A型电脑的销售量不小于B型电脑销售量的4倍.已知该公司在同一时期内销售这两种电脑共210台,则该公司在这一时期内销售这两种电脑能获得的最大利润是( )
A.42000元 B.46200元 C.52500元 D.63000元
4.“五一”期间,一体育用品商店搞优惠促销活动,其活动内容是:“凡在该商店一次性购物超过100元者,超过100元的部分按九折优惠”在此活动中,小东到该商店为学校一次性购买单价为70元的篮球个(),则小东应付货款(元)与篮球个数(个)的函数关系式是( )
A. B.
C. D.
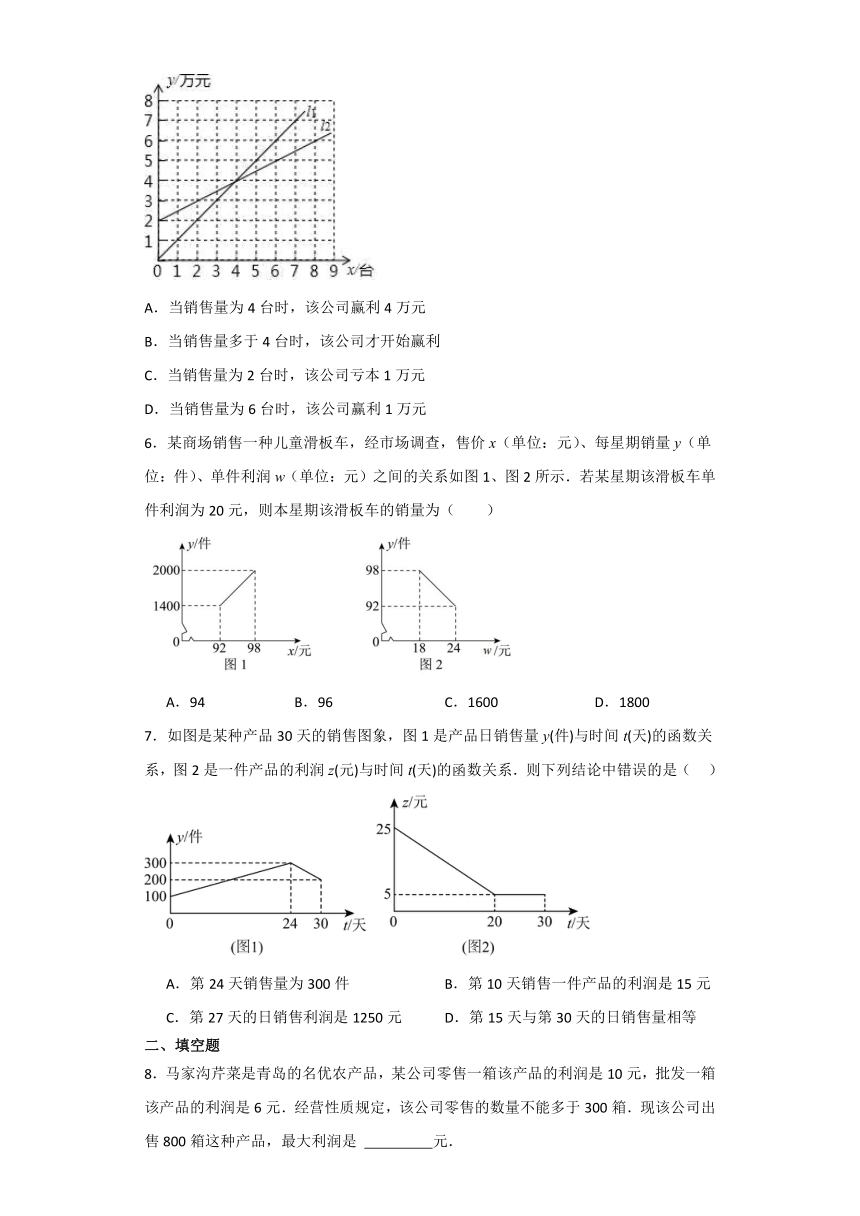
5.如图,l1反映了某公司销售一种医疗器械的销售收入(万元)与销售量(台)之间的关系,l2反映了该公司销售该种医疗器械的销售成本(万元)与销售量(台)之间的关系.当销售收入大于销售成本时,该医疗器械才开始赢利.根据图象,则下列判断中错误的是( )
当销售量为4台时,该公司赢利4万元
B.当销售量多于4台时,该公司才开始赢利
C.当销售量为2台时,该公司亏本1万元
D.当销售量为6台时,该公司赢利1万元
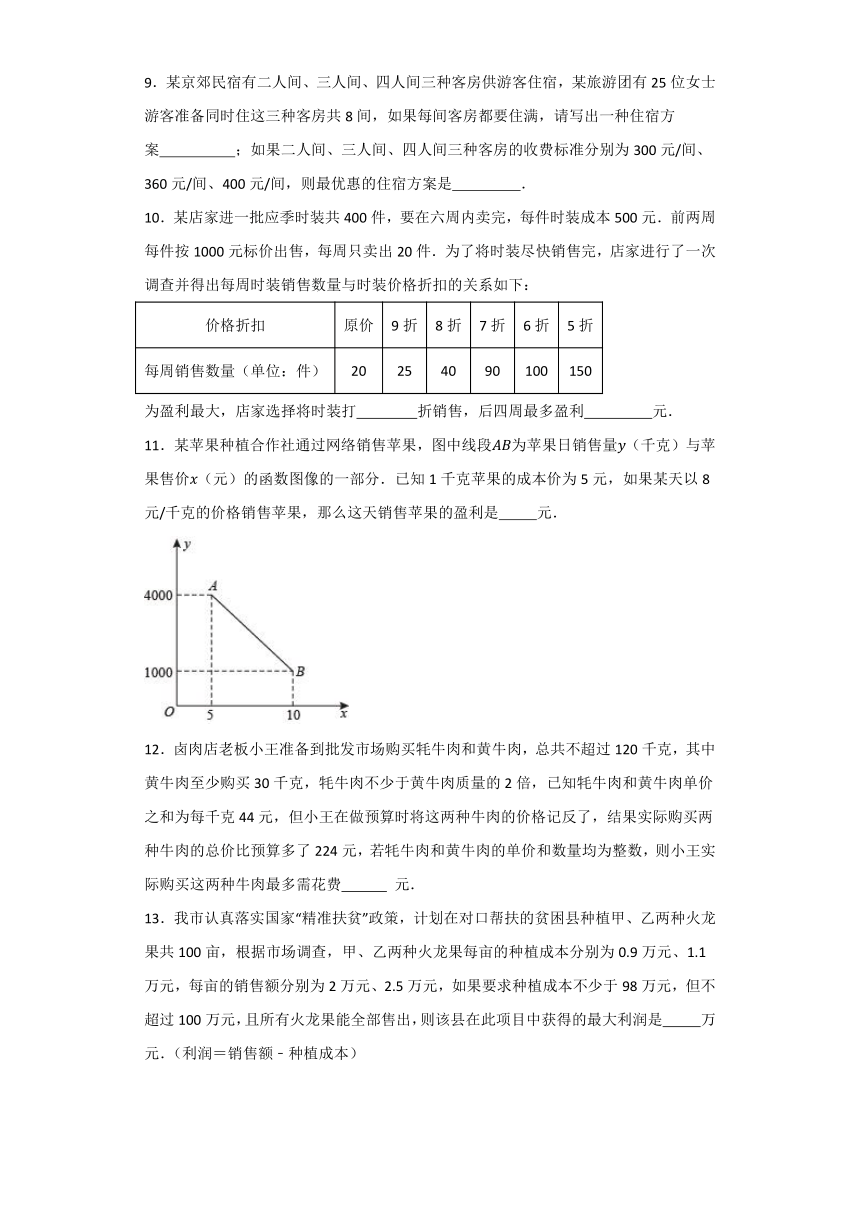
6.某商场销售一种儿童滑板车,经市场调查,售价x(单位:元)、每星期销量y(单位:件)、单件利润w(单位:元)之间的关系如图1、图2所示.若某星期该滑板车单件利润为20元,则本星期该滑板车的销量为( )
A.94 B.96 C.1600 D.1800
7.如图是某种产品30天的销售图象,图1是产品日销售量y(件)与时间t(天)的函数关系,图2是一件产品的利润z(元)与时间t(天)的函数关系.则下列结论中错误的是( )
A.第24天销售量为300件 B.第10天销售一件产品的利润是15元
C.第27天的日销售利润是1250元 D.第15天与第30天的日销售量相等
二、填空题
8.马家沟芹菜是青岛的名优农产品,某公司零售一箱该产品的利润是10元,批发一箱该产品的利润是6元.经营性质规定,该公司零售的数量不能多于300箱.现该公司出售800箱这种产品,最大利润是 元.
9.某京郊民宿有二人间、三人间、四人间三种客房供游客住宿,某旅游团有25位女士游客准备同时住这三种客房共8间,如果每间客房都要住满,请写出一种住宿方案 ;如果二人间、三人间、四人间三种客房的收费标准分别为300元/间、360元/间、400元/间,则最优惠的住宿方案是 .
10.某店家进一批应季时装共400件,要在六周内卖完,每件时装成本500元.前两周每件按1000元标价出售,每周只卖出20件.为了将时装尽快销售完,店家进行了一次调查并得出每周时装销售数量与时装价格折扣的关系如下:
价格折扣 原价 9折 8折 7折 6折 5折
每周销售数量(单位:件) 20 25 40 90 100 150
为盈利最大,店家选择将时装打 折销售,后四周最多盈利 元.
11.某苹果种植合作社通过网络销售苹果,图中线段为苹果日销售量(千克)与苹果售价(元)的函数图像的一部分.已知1千克苹果的成本价为5元,如果某天以8元/千克的价格销售苹果,那么这天销售苹果的盈利是 元.
12.卤肉店老板小王准备到批发市场购买牦牛肉和黄牛肉,总共不超过120千克,其中黄牛肉至少购买30千克,牦牛肉不少于黄牛肉质量的2倍,已知牦牛肉和黄牛肉单价之和为每千克44元,但小王在做预算时将这两种牛肉的价格记反了,结果实际购买两种牛肉的总价比预算多了224元,若牦牛肉和黄牛肉的单价和数量均为整数,则小王实际购买这两种牛肉最多需花费 元.
13.我市认真落实国家“精准扶贫”政策,计划在对口帮扶的贫困县种植甲、乙两种火龙果共100亩,根据市场调查,甲、乙两种火龙果每亩的种植成本分别为0.9万元、1.1万元,每亩的销售额分别为2万元、2.5万元,如果要求种植成本不少于98万元,但不超过100万元,且所有火龙果能全部售出,则该县在此项目中获得的最大利润是 万元.(利润=销售额﹣种植成本)
14.某公司新产品上市天全部售完,图1表示产品的市场日销售量与上市时间之间的关系,图2表示单件产品的销售利润与上市时间之间的关系,则最大日销售利润是 元.
三、解答题
15.“双减”政策受到各地教育部门的积极响应,学校为增加学生的课外活动实践,现决定增购两种体育器材:购买3件A种器材、4件B种器材需要180元,购买4件A种器材、3件B种器材需要170元.
(1)购买一件A种器材和一件B种器材各需要多少元?
(2)今年计划购买A、B两种体育器材共40件,且A种器材的数量不超过B种器材数量的3倍,那么购买A种器材和B种器材各多少件时花费最少?最少花费为多少元?
16.河南省开封市是中国历史文化名城,有“八朝古都”之称,每年都吸引了无数的游客前来观光,开封特产“花生糕”“菊花茶”“灌汤小笼包”等也大受欢迎.某经销商抓住商机,计划购进“花生糕”和“菊花茶”共100盒,已知购进10盒“花生糕”和20盒“菊花茶”共需620元,购进30盒“花生糕”和40盒“菊花茶”共需1360元.
(1)每盒“花生糕”和“菊花茶”的进价分别是多少元?
(2)结合游客的实际需求,该经销商决定购进“花生糕”的数量不超过“菊花茶”数量的,请你帮他计算如何进货才能使所花费用最少,最少费用是多少元?
17.某社区采购春节慰问礼品,购买了甲、乙两种类型的粮油套装.甲种粮油套装单价比乙种粮油套装单价多元,用元购买甲种粮油套装和用元购买乙种粮油套装的数量相同.
(1)求甲、乙两种粮油套装的单价分别是多少元?
(2)社区准备再次购买甲种和乙种粮油套装共件,购买乙种粮油套装不超过甲种粮油套装的倍,且商家给出了两种粮油套装均打八折的优惠.问购买甲种和乙种粮油套装各多少件时花费最少?最少花费是多少元?
18.某商场购进、两种商品共件进行销售,其中商品的件数不大于商品的件数,且不小于件,、两种商品的进价、售价如表:
进价元件
售价元件
请利用本章所学知识解决下列问题:
(1)设商场购进商品的件数为件,购进、两种商品全部售出后获得利润为元,求和之间的函数关系式,并写出的取值范围;
(2)在(1)的条件下,要使商场获得最大利润,该公司应购进多少件?最大利润是多少?
(3)在(1)的条件下,商场决定在销售活动中每售出一件,就从一件的利润中拿出元捐给慈善基金,则该商场应购进 件,方可获得最大利润.
19.为了缓解大气污染,贵阳市公交公司决定将某一条线路上的柴油公交车替换为新能源公交车,计划购买A型和B型两种新能源公交车共10辆.若购买A型公交车3辆,B型公交车 2辆,共需180万元;若购买A型公交车2辆,B型公交车3辆,共需195 万元.
(1)求购买A型和B型公交车每辆各需多少万元;
(2)预计在该线路上A型和B型公交车每辆年均载客量分别为60万人次和100 万人次,若该公司购买A型和B型公交车的总费用不超过 360万元,且确保这10辆公交车在该线路的年均载客总和不少于 680 万人次,则该公司有哪几种购车方案,哪种购车方案总费用最少 最少总费用是多少
20.我校举办了首届“数学展示”活动,为表彰在本次活动中表现优秀的学生,老师决定购买笔袋或彩色铅笔作为奖品.已知1个笔袋、2筒彩色铅笔原价共需44元;2个笔袋、3筒彩色铅笔原价共需73元.
(1)每个笔袋、每筒彩色铅笔原价各多少元
(2)正巧商家举行“优惠促销”活动,具体办法如下:笔袋“九折”优惠;彩色铅笔不超过10筒不优惠,超出10筒的部分“八折”优惠.若买个笔袋需要元,买筒彩色铅笔需要元.请用含的代数式表示;
(3)若在(2)的条件下购买同一种奖品100件,请你分析买哪种奖品省钱.
参考答案
1.解:∵凡在该商店一次性购物超过100元者,超过100元的部分按九折优惠,
∴李明到该商场为单位一次性买单价为60元的办公用品,x(x>2)件,
则李明应付贷款y(元)与办公用品件数x(件)的函数关系式是:
.
故答案选B.
2.解:设销售收入y(元)与销售量x(万件)的关系为y=kx+b,
由题意得,
解得,
∴y=5000x+3000,
∴当x=0时,y=3000,
即营销人员没有销售时的收入是3000元.
故选:B.
3.解:设该公司在这一时期内销售获得的利润是W元,销售A型电脑x台,则销售B型电脑台,
根据题意得:,
解得:,
∵,,
∴随的增大而减小,
∴当时,W取最大值,最大值为(元),
答:该公司在这一时期内销售这两种电脑能获得的最大利润是46200元.
故选:B.
4.解:∵凡在该商店一次性购物超过 100元者,超过100元的部分按九折优惠,
∴小东到该商店为学校一次性购买单价为70元的篮球x个(x>2),
则小东应付货款y(元)与篮球个数x(个)的函数关系式是:
y=(70x-100)×0.9+100=63x+10(x>2),
故选:C.
5.解:A、当销售量为4台时,该公司赢利0万元,错误;
B、当销售量多于4台时,该公司才开始赢利,正确;
C、当销售量为2台时,该公司亏本1万元,正确;
D、当销售量为6台时,该公司赢利1万元,正确;
故选A.
6.解:由图1可设y与x的函数解析式为y=kx+b,
把(92,1400)和(98,2000)代入得,
解得:,
∴y与x的函数解析式为:y=100x﹣7800;
由图2可设x与w的函数解析式为x=mw+n,
把(18,98)和(24,92)代入得:
解得:
∴x与w的函数解析式为:x=﹣w+116,
当w=20时,x=﹣20+116=96,
y=100×96﹣7800=9600﹣7800=1800(件),
∴本星期该滑板车的销量为1800件,
故选:D.
7.解:A、根据图①可得第24天的销售量为300件,故A正确;
B、设当0≤t≤20,一件产品的销售利润z(单位:元)与时间t(单位:天)的函数关系为z=kx+b,
把(0,25),(20,5)代入得:
,
解得:,
∴z=-x+25,
当x=10时,z=-10+25=15,
故B正确;
C、当24≤t≤30时,设产品日销售量y(单位:件)与时间t(单位;天)的函数关系为y=k1t+b1,
把(30,200),(24,300)代入得:
,
解得:
∴y=-+700,
当t=27时,y=250,
∴第27天的日销售利润为;250×5=1250(元),故C正确;
D、当0<t<24时,可得y=t+100,t=15时,y≠200,故D错误,
故选D.
8.解:设该公司当月零售这种农产品m箱,则批发这种农产品箱,依题意得:,
设该公司获得利润为y元,依题意得:
,
即,
∵,y随着m的增大而增大,
∴当时,y取最大值,此时(元),
答:该公司要经营800箱这种农产品,最大利润是6000元.
故答案为:6000.
9.解:设二人间、三人间分别需要间,间,则四人间需要间,则
,
整理得:,
∵,,都为非负整数,
∴当时,,,
∴可行的住宿方案为:二人间2间,三人间3间,四人间3间;
设住宿总费用为:元,而,则
,
∵,
∴当最大,有最小值,
∵,,,都为非负整数,
∴时最大,
此时,;
∴最佳住宿方案为:二人间3间,三人间1间,四人间4间.
故答案为:二人间2间,三人间3间,四人间3间(答案不唯一);二人间3间,三人间1间,四人间4间.
10.解:设后四周的利润为w,折扣为x,
由题意,前两周已售出40件,
∴剩余360件应在余下4周内售完,
由表格分析可知,折扣在8折及以下时,无法满足尽快售完的条件,
∴要满足条件应该选择8折以上的折扣,
∴,
其中,,
∵,
∴w随x的增大而增大,
∴当时,w取最大值,此时,
∴当折扣为7折时,后四周利润最大,最大利润为72000元,
故答案为:7;72000.
11.解:设线段AB的解析式为y=kx+b,点A、B的坐标代入,得
,解得,
∴y=-600x+7000,
当x=8时,y=,
∴这天销售苹果的盈利是=6600(元),
故答案为:6600.
12.解:设牦牛肉和黄牛肉的单价分别为每千克x元和(44-x)元,购买牛肉牦牛肉和黄牛肉的数量分别为m千克和n千克;
由题意:mx+n(44-x)-[m(44-x)+nx]=224,
∴x(m-n)=22(m-n)+112,
∵实际购买这两种牛肉的价格=mx+n(44-x)=x(m-n)+44n=22(m+n)+112,
∵m+n≤120,
∴当m+n=120时,22(m+n)+112有最大值,最大值=2752(元),
答:小游实际购买这两种牛肉最多需要花费2752元.
13.解:设甲种火龙果种植亩,乙钟火龙果种植亩,此项目获得利润,
甲、乙两种火龙果每亩利润为1.1万元,1.4万元,
由题意可知:,
解得:,
此项目获得利润,
∵
∴随的增大而减小,
∴当时,
的最大值为万元,
故答案为:125.
14.解:由图1知,当天数t=30时,市场日销售量达到最大60件;
从图2知,当天数t=30时,每件产品销售利润达到最大30元,
所以当天数t=30时,市场的日销售利润最大,最大利润为60×30=1800元,
故答案为:1800
15.解:(1)设购买一件A种器材需要x元,购买一件B种器材需要y元
由题意得:,解得:
答:设购买一件A种器材需要20元,购买一件B种器材需要30元.
(2)设购买A种器材a件,则购买B种器材件,总费用为w元.
由题意得:,解得:,
由题意得:,
∵,∴w随a的增大而减小,
∴当时,w的值最小,.
答:购买A种器材30件,购买B种器材10件时花费最少,最少花费为900元.
16.(1)解:设花生糕每盒进价x元,菊花茶商品每盒进价y元,得
,
解得:,
答:花生糕每盒进价12元,菊花茶商品每盒进价25元;
(2)解:设花生糕进a盒,菊花茶进盒,由题意得,
,
,
设花费为y元,则,
,
∵,则y随a的增大而减小,
∴要使花费最少,则a取最大值,
∵a为整数且,
∴时,花费最少,
∴,
,
答:花生糕进40盒,菊花茶商品进60盒,花费最少是1980元.
17.(1)解:设乙种粮油套装的单价为元,则甲种粮油套装的单价为元,
由题意可得,,
解得,
经检验,是原方程的解,符合题意,
∴,
答:甲种粮油套装的单价为元,乙种粮油套装的单价为元;
(2)解:设购买了甲种粮油套装件,则乙种粮油套装件,费用为元,
则 ,
∵购买乙种粮油套装不超过甲种粮油套装的倍,
∴,
解得,
∴当时,即购买甲种粮油套装件,乙种粮油套装件,花费最少,
此时,元.
18.(1)解:由题意可得,
,
商品的件数不大于商品的件数,且不小于件,
,
解得,
即与之间的函数关系式是;
(2)与之间的函数关系式是;
随的增大而增大,
当时,利润最大,最大利润为:.
(3)设最后获得的利润为元,
由题意可得:,
,
,
随的增大而减小,
,
当时,取得最大值,此时,
答:该商场应购进商品件,方可获得最大利润.
故答案为:.
19.解:(1)设购买每辆A型公交车需要x万元,每辆B型公交车需要y万元,
依题意,得: ,解得:
答:购买每辆A型公交车需要30万元,每辆B型公交车需要45万元.
(2)设购进A型公交车m辆,则购进B型公交车辆,
依题意,得:,
解得:,因为m为整数,所有,
所以,该公司有三种购车方案,
方案1:购进6辆A型公交车,4辆B型公交车;
方案2:购进7辆A型公交车,3辆B型公交车;
方案3:购进8辆A型公交车,2辆B型公交车.
该公司购买这10辆公交车的总费用为w元,则
,
因为,,w随m的增大而减小,当时,w取得最小值,最小值为330,
答:购进8辆A型公交车,2辆B型公交车时总费用最少,最少费用为330万元.
20.(1)解:设每个笔袋原价元,每筒彩色铅笔原价元,根据题意,得:
解得:
所以每个笔袋原价14元,每筒彩色铅笔原价15元.
(2),
当超过10筒时:即,
(3)当时,有,解得,因此当购买同一种奖品的数量少于50件时,买笔袋省钱.
当时,有,解得,因此当购买同一种奖品的数量为50件时,两者费用一样.
当时,有,解得,因此当购买同一种奖品的数量大于50件时,买彩色铅笔省钱.
奖品的数量为100件,,
买彩色铅笔省钱.
一、单选题
1.元旦期间,某商场搞优惠促销活动,其活动内容是:“凡在本商场一次性购物超过100元者,超过100元的部分按9折优惠”.在此活动中,李明到该商场为单位一次性购买单价为60元的办公用品x(x>2)件,则应付款y(元)与商品件数x(件)之间的关系式是( )
A.y=54x B.y=54x+10
C.y=54x-90 D.y=54x+45
2.某公司市场营销部的个人收入(元)与其每月的销售量(万件)成一次函数关系,其图象如图所示,营销人员没有销售时(最低工资)的收入是( )
A.2000元 B.3000元 C.3500元 D.4000元
3.某电脑公司经营A,B两种台式电脑,分析过去的销售记录可以知道:每台A型电脑可盈利200元,每台B型电脑可盈利300元;在同一时期内,A型电脑的销售量不小于B型电脑销售量的4倍.已知该公司在同一时期内销售这两种电脑共210台,则该公司在这一时期内销售这两种电脑能获得的最大利润是( )
A.42000元 B.46200元 C.52500元 D.63000元
4.“五一”期间,一体育用品商店搞优惠促销活动,其活动内容是:“凡在该商店一次性购物超过100元者,超过100元的部分按九折优惠”在此活动中,小东到该商店为学校一次性购买单价为70元的篮球个(),则小东应付货款(元)与篮球个数(个)的函数关系式是( )
A. B.
C. D.
5.如图,l1反映了某公司销售一种医疗器械的销售收入(万元)与销售量(台)之间的关系,l2反映了该公司销售该种医疗器械的销售成本(万元)与销售量(台)之间的关系.当销售收入大于销售成本时,该医疗器械才开始赢利.根据图象,则下列判断中错误的是( )
当销售量为4台时,该公司赢利4万元
B.当销售量多于4台时,该公司才开始赢利
C.当销售量为2台时,该公司亏本1万元
D.当销售量为6台时,该公司赢利1万元
6.某商场销售一种儿童滑板车,经市场调查,售价x(单位:元)、每星期销量y(单位:件)、单件利润w(单位:元)之间的关系如图1、图2所示.若某星期该滑板车单件利润为20元,则本星期该滑板车的销量为( )
A.94 B.96 C.1600 D.1800
7.如图是某种产品30天的销售图象,图1是产品日销售量y(件)与时间t(天)的函数关系,图2是一件产品的利润z(元)与时间t(天)的函数关系.则下列结论中错误的是( )
A.第24天销售量为300件 B.第10天销售一件产品的利润是15元
C.第27天的日销售利润是1250元 D.第15天与第30天的日销售量相等
二、填空题
8.马家沟芹菜是青岛的名优农产品,某公司零售一箱该产品的利润是10元,批发一箱该产品的利润是6元.经营性质规定,该公司零售的数量不能多于300箱.现该公司出售800箱这种产品,最大利润是 元.
9.某京郊民宿有二人间、三人间、四人间三种客房供游客住宿,某旅游团有25位女士游客准备同时住这三种客房共8间,如果每间客房都要住满,请写出一种住宿方案 ;如果二人间、三人间、四人间三种客房的收费标准分别为300元/间、360元/间、400元/间,则最优惠的住宿方案是 .
10.某店家进一批应季时装共400件,要在六周内卖完,每件时装成本500元.前两周每件按1000元标价出售,每周只卖出20件.为了将时装尽快销售完,店家进行了一次调查并得出每周时装销售数量与时装价格折扣的关系如下:
价格折扣 原价 9折 8折 7折 6折 5折
每周销售数量(单位:件) 20 25 40 90 100 150
为盈利最大,店家选择将时装打 折销售,后四周最多盈利 元.
11.某苹果种植合作社通过网络销售苹果,图中线段为苹果日销售量(千克)与苹果售价(元)的函数图像的一部分.已知1千克苹果的成本价为5元,如果某天以8元/千克的价格销售苹果,那么这天销售苹果的盈利是 元.
12.卤肉店老板小王准备到批发市场购买牦牛肉和黄牛肉,总共不超过120千克,其中黄牛肉至少购买30千克,牦牛肉不少于黄牛肉质量的2倍,已知牦牛肉和黄牛肉单价之和为每千克44元,但小王在做预算时将这两种牛肉的价格记反了,结果实际购买两种牛肉的总价比预算多了224元,若牦牛肉和黄牛肉的单价和数量均为整数,则小王实际购买这两种牛肉最多需花费 元.
13.我市认真落实国家“精准扶贫”政策,计划在对口帮扶的贫困县种植甲、乙两种火龙果共100亩,根据市场调查,甲、乙两种火龙果每亩的种植成本分别为0.9万元、1.1万元,每亩的销售额分别为2万元、2.5万元,如果要求种植成本不少于98万元,但不超过100万元,且所有火龙果能全部售出,则该县在此项目中获得的最大利润是 万元.(利润=销售额﹣种植成本)
14.某公司新产品上市天全部售完,图1表示产品的市场日销售量与上市时间之间的关系,图2表示单件产品的销售利润与上市时间之间的关系,则最大日销售利润是 元.
三、解答题
15.“双减”政策受到各地教育部门的积极响应,学校为增加学生的课外活动实践,现决定增购两种体育器材:购买3件A种器材、4件B种器材需要180元,购买4件A种器材、3件B种器材需要170元.
(1)购买一件A种器材和一件B种器材各需要多少元?
(2)今年计划购买A、B两种体育器材共40件,且A种器材的数量不超过B种器材数量的3倍,那么购买A种器材和B种器材各多少件时花费最少?最少花费为多少元?
16.河南省开封市是中国历史文化名城,有“八朝古都”之称,每年都吸引了无数的游客前来观光,开封特产“花生糕”“菊花茶”“灌汤小笼包”等也大受欢迎.某经销商抓住商机,计划购进“花生糕”和“菊花茶”共100盒,已知购进10盒“花生糕”和20盒“菊花茶”共需620元,购进30盒“花生糕”和40盒“菊花茶”共需1360元.
(1)每盒“花生糕”和“菊花茶”的进价分别是多少元?
(2)结合游客的实际需求,该经销商决定购进“花生糕”的数量不超过“菊花茶”数量的,请你帮他计算如何进货才能使所花费用最少,最少费用是多少元?
17.某社区采购春节慰问礼品,购买了甲、乙两种类型的粮油套装.甲种粮油套装单价比乙种粮油套装单价多元,用元购买甲种粮油套装和用元购买乙种粮油套装的数量相同.
(1)求甲、乙两种粮油套装的单价分别是多少元?
(2)社区准备再次购买甲种和乙种粮油套装共件,购买乙种粮油套装不超过甲种粮油套装的倍,且商家给出了两种粮油套装均打八折的优惠.问购买甲种和乙种粮油套装各多少件时花费最少?最少花费是多少元?
18.某商场购进、两种商品共件进行销售,其中商品的件数不大于商品的件数,且不小于件,、两种商品的进价、售价如表:
进价元件
售价元件
请利用本章所学知识解决下列问题:
(1)设商场购进商品的件数为件,购进、两种商品全部售出后获得利润为元,求和之间的函数关系式,并写出的取值范围;
(2)在(1)的条件下,要使商场获得最大利润,该公司应购进多少件?最大利润是多少?
(3)在(1)的条件下,商场决定在销售活动中每售出一件,就从一件的利润中拿出元捐给慈善基金,则该商场应购进 件,方可获得最大利润.
19.为了缓解大气污染,贵阳市公交公司决定将某一条线路上的柴油公交车替换为新能源公交车,计划购买A型和B型两种新能源公交车共10辆.若购买A型公交车3辆,B型公交车 2辆,共需180万元;若购买A型公交车2辆,B型公交车3辆,共需195 万元.
(1)求购买A型和B型公交车每辆各需多少万元;
(2)预计在该线路上A型和B型公交车每辆年均载客量分别为60万人次和100 万人次,若该公司购买A型和B型公交车的总费用不超过 360万元,且确保这10辆公交车在该线路的年均载客总和不少于 680 万人次,则该公司有哪几种购车方案,哪种购车方案总费用最少 最少总费用是多少
20.我校举办了首届“数学展示”活动,为表彰在本次活动中表现优秀的学生,老师决定购买笔袋或彩色铅笔作为奖品.已知1个笔袋、2筒彩色铅笔原价共需44元;2个笔袋、3筒彩色铅笔原价共需73元.
(1)每个笔袋、每筒彩色铅笔原价各多少元
(2)正巧商家举行“优惠促销”活动,具体办法如下:笔袋“九折”优惠;彩色铅笔不超过10筒不优惠,超出10筒的部分“八折”优惠.若买个笔袋需要元,买筒彩色铅笔需要元.请用含的代数式表示;
(3)若在(2)的条件下购买同一种奖品100件,请你分析买哪种奖品省钱.
参考答案
1.解:∵凡在该商店一次性购物超过100元者,超过100元的部分按九折优惠,
∴李明到该商场为单位一次性买单价为60元的办公用品,x(x>2)件,
则李明应付贷款y(元)与办公用品件数x(件)的函数关系式是:
.
故答案选B.
2.解:设销售收入y(元)与销售量x(万件)的关系为y=kx+b,
由题意得,
解得,
∴y=5000x+3000,
∴当x=0时,y=3000,
即营销人员没有销售时的收入是3000元.
故选:B.
3.解:设该公司在这一时期内销售获得的利润是W元,销售A型电脑x台,则销售B型电脑台,
根据题意得:,
解得:,
∵,,
∴随的增大而减小,
∴当时,W取最大值,最大值为(元),
答:该公司在这一时期内销售这两种电脑能获得的最大利润是46200元.
故选:B.
4.解:∵凡在该商店一次性购物超过 100元者,超过100元的部分按九折优惠,
∴小东到该商店为学校一次性购买单价为70元的篮球x个(x>2),
则小东应付货款y(元)与篮球个数x(个)的函数关系式是:
y=(70x-100)×0.9+100=63x+10(x>2),
故选:C.
5.解:A、当销售量为4台时,该公司赢利0万元,错误;
B、当销售量多于4台时,该公司才开始赢利,正确;
C、当销售量为2台时,该公司亏本1万元,正确;
D、当销售量为6台时,该公司赢利1万元,正确;
故选A.
6.解:由图1可设y与x的函数解析式为y=kx+b,
把(92,1400)和(98,2000)代入得,
解得:,
∴y与x的函数解析式为:y=100x﹣7800;
由图2可设x与w的函数解析式为x=mw+n,
把(18,98)和(24,92)代入得:
解得:
∴x与w的函数解析式为:x=﹣w+116,
当w=20时,x=﹣20+116=96,
y=100×96﹣7800=9600﹣7800=1800(件),
∴本星期该滑板车的销量为1800件,
故选:D.
7.解:A、根据图①可得第24天的销售量为300件,故A正确;
B、设当0≤t≤20,一件产品的销售利润z(单位:元)与时间t(单位:天)的函数关系为z=kx+b,
把(0,25),(20,5)代入得:
,
解得:,
∴z=-x+25,
当x=10时,z=-10+25=15,
故B正确;
C、当24≤t≤30时,设产品日销售量y(单位:件)与时间t(单位;天)的函数关系为y=k1t+b1,
把(30,200),(24,300)代入得:
,
解得:
∴y=-+700,
当t=27时,y=250,
∴第27天的日销售利润为;250×5=1250(元),故C正确;
D、当0<t<24时,可得y=t+100,t=15时,y≠200,故D错误,
故选D.
8.解:设该公司当月零售这种农产品m箱,则批发这种农产品箱,依题意得:,
设该公司获得利润为y元,依题意得:
,
即,
∵,y随着m的增大而增大,
∴当时,y取最大值,此时(元),
答:该公司要经营800箱这种农产品,最大利润是6000元.
故答案为:6000.
9.解:设二人间、三人间分别需要间,间,则四人间需要间,则
,
整理得:,
∵,,都为非负整数,
∴当时,,,
∴可行的住宿方案为:二人间2间,三人间3间,四人间3间;
设住宿总费用为:元,而,则
,
∵,
∴当最大,有最小值,
∵,,,都为非负整数,
∴时最大,
此时,;
∴最佳住宿方案为:二人间3间,三人间1间,四人间4间.
故答案为:二人间2间,三人间3间,四人间3间(答案不唯一);二人间3间,三人间1间,四人间4间.
10.解:设后四周的利润为w,折扣为x,
由题意,前两周已售出40件,
∴剩余360件应在余下4周内售完,
由表格分析可知,折扣在8折及以下时,无法满足尽快售完的条件,
∴要满足条件应该选择8折以上的折扣,
∴,
其中,,
∵,
∴w随x的增大而增大,
∴当时,w取最大值,此时,
∴当折扣为7折时,后四周利润最大,最大利润为72000元,
故答案为:7;72000.
11.解:设线段AB的解析式为y=kx+b,点A、B的坐标代入,得
,解得,
∴y=-600x+7000,
当x=8时,y=,
∴这天销售苹果的盈利是=6600(元),
故答案为:6600.
12.解:设牦牛肉和黄牛肉的单价分别为每千克x元和(44-x)元,购买牛肉牦牛肉和黄牛肉的数量分别为m千克和n千克;
由题意:mx+n(44-x)-[m(44-x)+nx]=224,
∴x(m-n)=22(m-n)+112,
∵实际购买这两种牛肉的价格=mx+n(44-x)=x(m-n)+44n=22(m+n)+112,
∵m+n≤120,
∴当m+n=120时,22(m+n)+112有最大值,最大值=2752(元),
答:小游实际购买这两种牛肉最多需要花费2752元.
13.解:设甲种火龙果种植亩,乙钟火龙果种植亩,此项目获得利润,
甲、乙两种火龙果每亩利润为1.1万元,1.4万元,
由题意可知:,
解得:,
此项目获得利润,
∵
∴随的增大而减小,
∴当时,
的最大值为万元,
故答案为:125.
14.解:由图1知,当天数t=30时,市场日销售量达到最大60件;
从图2知,当天数t=30时,每件产品销售利润达到最大30元,
所以当天数t=30时,市场的日销售利润最大,最大利润为60×30=1800元,
故答案为:1800
15.解:(1)设购买一件A种器材需要x元,购买一件B种器材需要y元
由题意得:,解得:
答:设购买一件A种器材需要20元,购买一件B种器材需要30元.
(2)设购买A种器材a件,则购买B种器材件,总费用为w元.
由题意得:,解得:,
由题意得:,
∵,∴w随a的增大而减小,
∴当时,w的值最小,.
答:购买A种器材30件,购买B种器材10件时花费最少,最少花费为900元.
16.(1)解:设花生糕每盒进价x元,菊花茶商品每盒进价y元,得
,
解得:,
答:花生糕每盒进价12元,菊花茶商品每盒进价25元;
(2)解:设花生糕进a盒,菊花茶进盒,由题意得,
,
,
设花费为y元,则,
,
∵,则y随a的增大而减小,
∴要使花费最少,则a取最大值,
∵a为整数且,
∴时,花费最少,
∴,
,
答:花生糕进40盒,菊花茶商品进60盒,花费最少是1980元.
17.(1)解:设乙种粮油套装的单价为元,则甲种粮油套装的单价为元,
由题意可得,,
解得,
经检验,是原方程的解,符合题意,
∴,
答:甲种粮油套装的单价为元,乙种粮油套装的单价为元;
(2)解:设购买了甲种粮油套装件,则乙种粮油套装件,费用为元,
则 ,
∵购买乙种粮油套装不超过甲种粮油套装的倍,
∴,
解得,
∴当时,即购买甲种粮油套装件,乙种粮油套装件,花费最少,
此时,元.
18.(1)解:由题意可得,
,
商品的件数不大于商品的件数,且不小于件,
,
解得,
即与之间的函数关系式是;
(2)与之间的函数关系式是;
随的增大而增大,
当时,利润最大,最大利润为:.
(3)设最后获得的利润为元,
由题意可得:,
,
,
随的增大而减小,
,
当时,取得最大值,此时,
答:该商场应购进商品件,方可获得最大利润.
故答案为:.
19.解:(1)设购买每辆A型公交车需要x万元,每辆B型公交车需要y万元,
依题意,得: ,解得:
答:购买每辆A型公交车需要30万元,每辆B型公交车需要45万元.
(2)设购进A型公交车m辆,则购进B型公交车辆,
依题意,得:,
解得:,因为m为整数,所有,
所以,该公司有三种购车方案,
方案1:购进6辆A型公交车,4辆B型公交车;
方案2:购进7辆A型公交车,3辆B型公交车;
方案3:购进8辆A型公交车,2辆B型公交车.
该公司购买这10辆公交车的总费用为w元,则
,
因为,,w随m的增大而减小,当时,w取得最小值,最小值为330,
答:购进8辆A型公交车,2辆B型公交车时总费用最少,最少费用为330万元.
20.(1)解:设每个笔袋原价元,每筒彩色铅笔原价元,根据题意,得:
解得:
所以每个笔袋原价14元,每筒彩色铅笔原价15元.
(2),
当超过10筒时:即,
(3)当时,有,解得,因此当购买同一种奖品的数量少于50件时,买笔袋省钱.
当时,有,解得,因此当购买同一种奖品的数量为50件时,两者费用一样.
当时,有,解得,因此当购买同一种奖品的数量大于50件时,买彩色铅笔省钱.
奖品的数量为100件,,
买彩色铅笔省钱.
