19.3课题学习-选择方案-—次函数的实际应用-行程问题 专题提升训练(含解析)2023—2024学年人教版八年级数学下册
文档属性
| 名称 | 19.3课题学习-选择方案-—次函数的实际应用-行程问题 专题提升训练(含解析)2023—2024学年人教版八年级数学下册 |
|
|
| 格式 | docx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-04-18 00:00:00 | ||
图片预览


文档简介
2023-2024学年人教版八年级数学下册《19.3课题学习-选择方案-—次函数的实际应用-行程问题》专题提升训练(附答案)
一、单选题
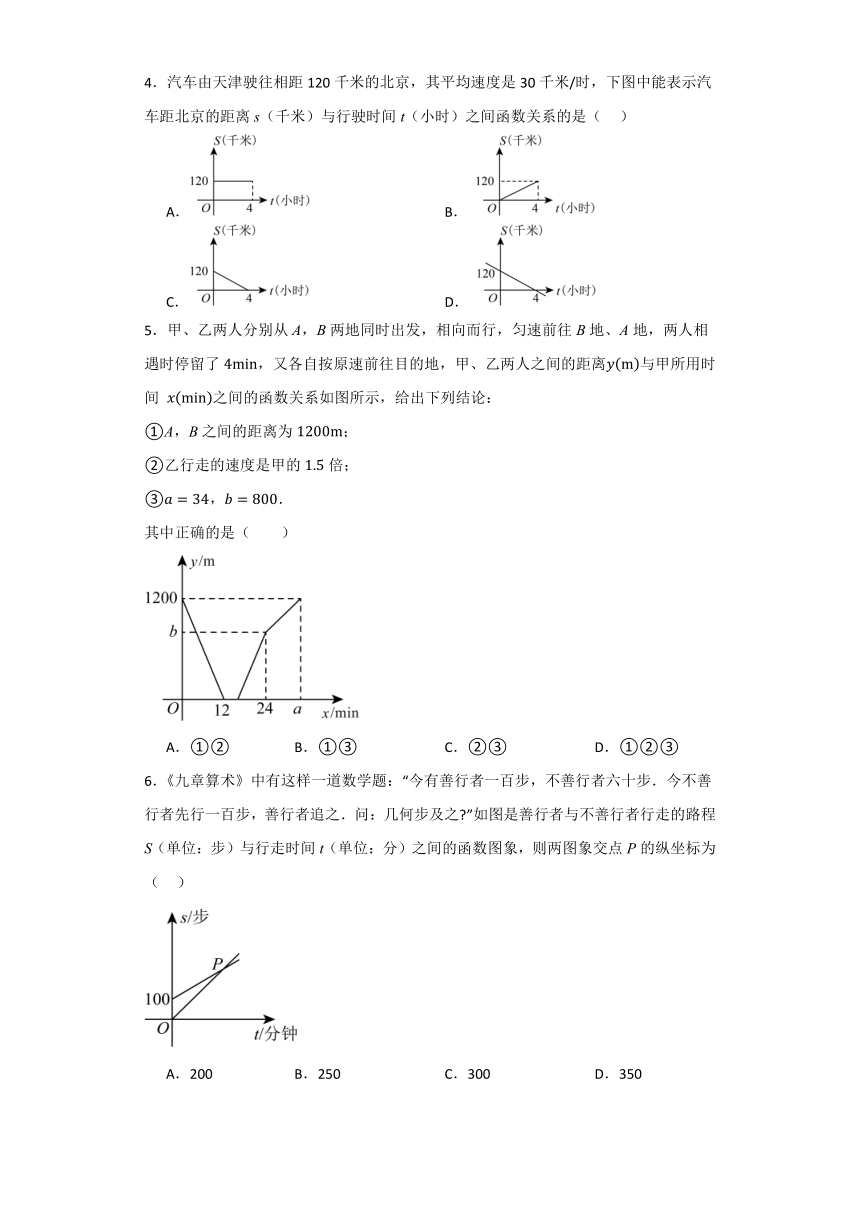
1.图中反映某网约车平台收费y(元)与所行驶的路程x(千米)的函数关系,根据图中的信息,当小明通过该网约车从家到机场共收费64元,若车速始终保持60千米/时不变,不考虑其它因素(红绿灯、堵车等),他从家到机场需要( )
A.10分钟 B.15分钟 C.18分钟 D.20分钟
2.小明和爸爸两人从相距4千米的甲地前往乙地,两人同时出发,小明骑自行车,爸爸骑电瓶车.线段,折线分别表示小明和爸爸距离甲地路程S(千米)与时间t(分)之间的函数关系.下列说法正确的是( )
A.小明骑车速度为千米/小时 B.爸爸中途停留了20分钟
C.小明在第15分钟追上爸爸 D.小明比爸爸早到5分钟
3.一辆快车和一辆慢车将一批物资从甲地运往乙地,其中快车送达后立即沿原路返回,且往返速度不变.两车离甲地的距离与慢车行驶时间的函数关系如图所示,那么两车先后两次相遇的间隔时间为( )
A. B. C. D.
4.汽车由天津驶往相距120千米的北京,其平均速度是30千米/时,下图中能表示汽车距北京的距离s(千米)与行驶时间t(小时)之间函数关系的是( )
A. B.
C. D.
5.甲、乙两人分别从A,B两地同时出发,相向而行,匀速前往B地、A地,两人相遇时停留了,又各自按原速前往目的地,甲、乙两人之间的距离与甲所用时间 之间的函数关系如图所示,给出下列结论:
①A,B之间的距离为;
②乙行走的速度是甲的倍;
③,.
其中正确的是( )
A.①② B.①③ C.②③ D.①②③
6.《九章算术》中有这样一道数学题:“今有善行者一百步,不善行者六十步.今不善行者先行一百步,善行者追之.问:几何步及之 ”如图是善行者与不善行者行走的路程S(单位:步)与行走时间t(单位:分)之间的函数图象,则两图象交点P的纵坐标为( )
A.200 B.250 C.300 D.350
7.如图(折线)描述了一辆汽车在某一直路上行驶的过程中,汽车离出发地的距离(千米)与行驶时间(小时)之间的变量关系,根据图中提供的信息,给出下列说法:
①汽车共行驶了100千米;②汽车在1.5至2小时之间匀速行驶;③汽车在整个行驶过程中(含停留过程)的平均速度为千米/时;④汽车出发后3小时至4.5小时之间,其行驶的速度在逐渐减小,其中正确的是( )
A.① B.② C.③ D.④
二、填空题
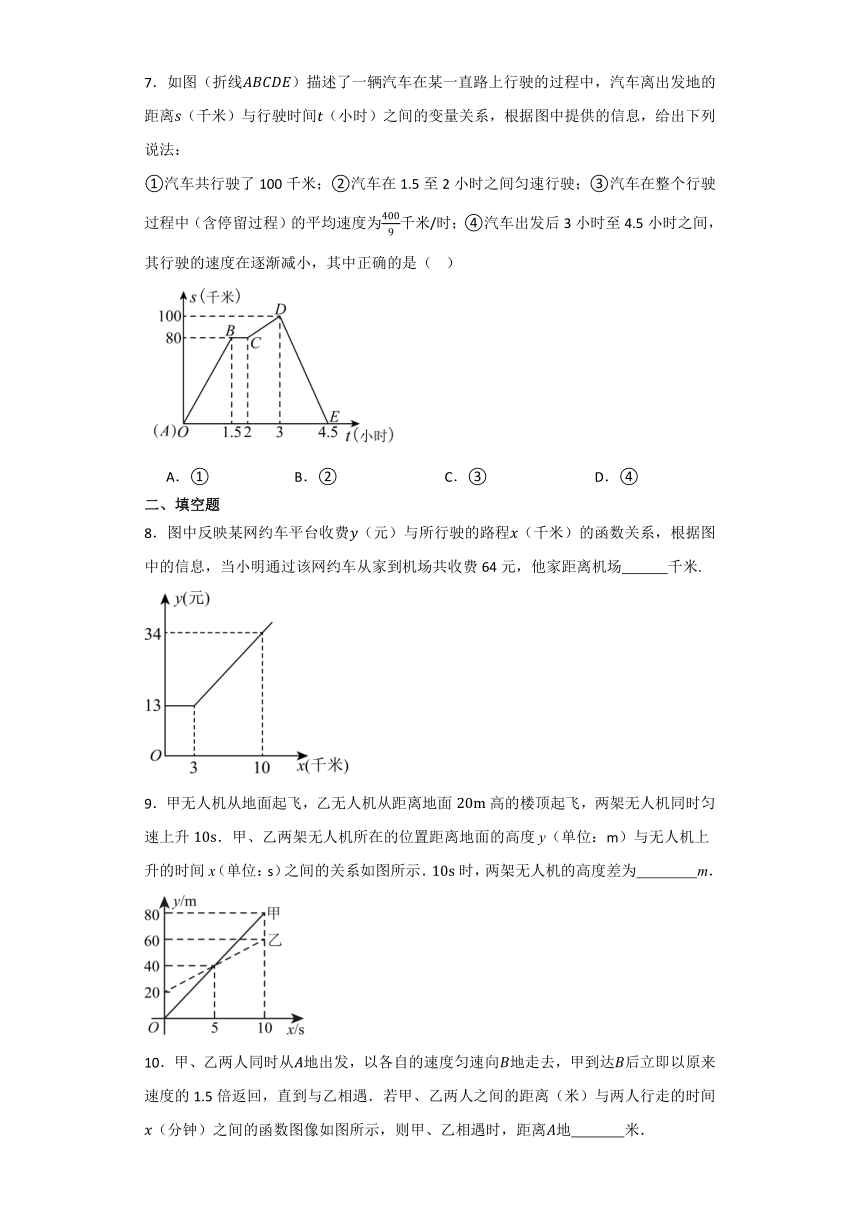
8.图中反映某网约车平台收费(元)与所行驶的路程(千米)的函数关系,根据图中的信息,当小明通过该网约车从家到机场共收费64元,他家距离机场 千米.
9.甲无人机从地面起飞,乙无人机从距离地面高的楼顶起飞,两架无人机同时匀速上升.甲、乙两架无人机所在的位置距离地面的高度y(单位:m)与无人机上升的时间x(单位:s)之间的关系如图所示.时,两架无人机的高度差为 m.
10.甲、乙两人同时从地出发,以各自的速度匀速向地走去,甲到达后立即以原来速度的1.5倍返回,直到与乙相遇.若甲、乙两人之间的距离(米)与两人行走的时间(分钟)之间的函数图像如图所示,则甲、乙相遇时,距离地 米.
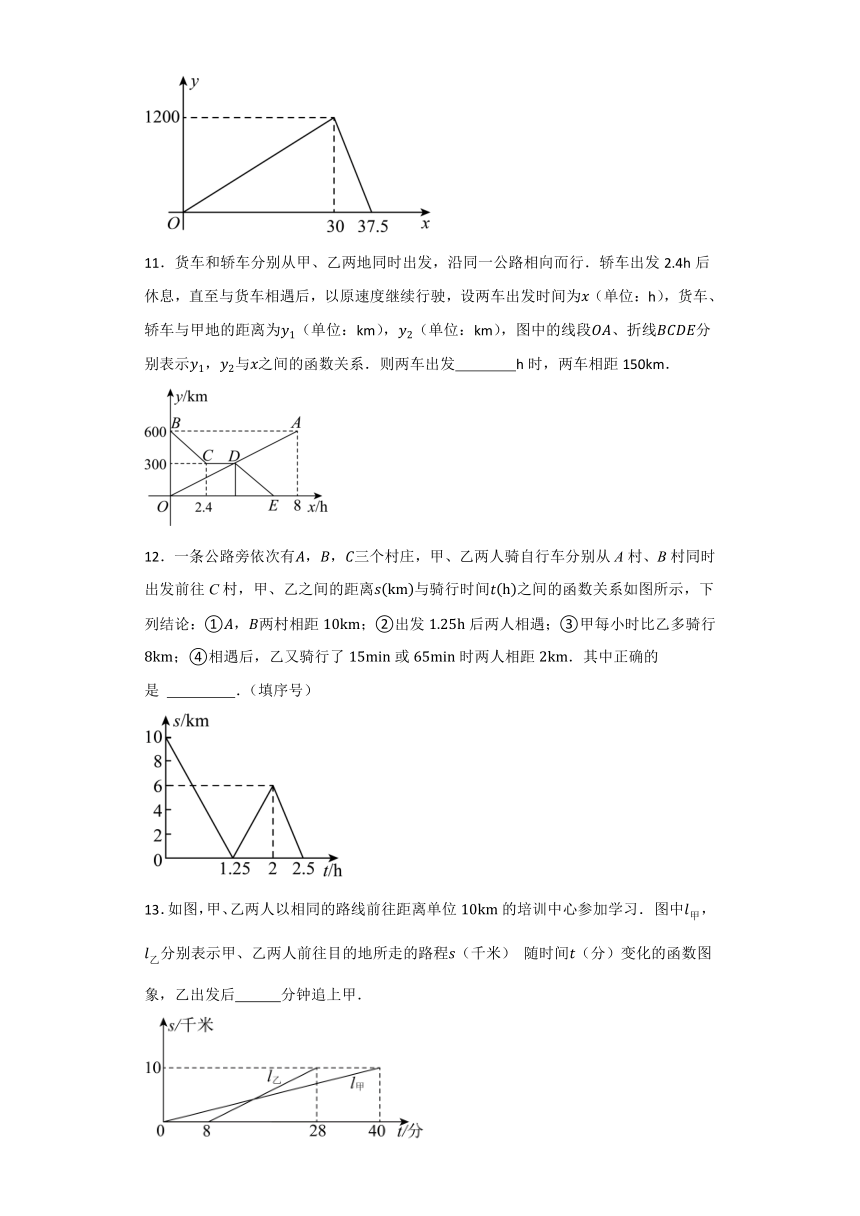
11.货车和轿车分别从甲、乙两地同时出发,沿同一公路相向而行.轿车出发2.4h后休息,直至与货车相遇后,以原速度继续行驶,设两车出发时间为(单位:h),货车、轿车与甲地的距离为(单位:km),(单位:km),图中的线段、折线分别表示,与之间的函数关系.则两车出发 h时,两车相距150km.
12.一条公路旁依次有三个村庄,甲、乙两人骑自行车分别从A村、B村同时出发前往C村,甲、乙之间的距离与骑行时间之间的函数关系如图所示,下列结论:①两村相距;②出发后两人相遇;③甲每小时比乙多骑行;④相遇后,乙又骑行了或时两人相距.其中正确的是 .(填序号)
13.如图,甲、乙两人以相同的路线前往距离单位的培训中心参加学习. 图中分别表示甲、乙两人前往目的地所走的路程(千米) 随时间(分)变化的函数图象,乙出发后 分钟追上甲.
14.如图所示,一列快车从甲地驶往乙地,一列慢车从乙地驶往甲地,两车同时出发,设慢车行驶的时间为,两车之间的距离为,图中的折线表示y与x之间的关系,下列说法中正确的为 .
①甲乙两地相距;②C点表示快车到达乙地;③快车的速度为;④慢车的速度为;⑤快车到达乙地后,慢车到达甲地.
三、解答题
15.2023年,哈尔滨的“冰雪大世界”吸引了众多游客,小明的爸爸将容量为60升的私家车油箱加满后,带着全家从大连自驾到哈尔滨游玩,行驶过程中,车离哈尔滨的路程(千米)与行驶时间(小时)的关系如图所示(中途休息、加油的时间不计).当油箱中剩余油量不超过10升时,车会自动显示加油提醒.设车平均耗油量为0.1升/千米,请根据图象解答下列问题:
(1)直接写出大连到哈尔滨的路程___________千米;
(2)求关于的函数表达式;
(3)当车显示加油提醒后,问行驶时间在怎样的范围内车应进站加油?
16.能源和环境问题是目前全球性急需解决的问题,虽然近百年人类文明有了前所未有的发展,但对于能源的使用和环境的破坏也造成了严重的后果,发展新能源是时代的要求,是未来生存的要求.新能源汽车不仅对环境保护具有重大的意义而且还能够减少对不可再生资源的开发,是全球汽车发展的重要方向.为了解某品牌一款新能源汽车的耗电量,相关技术人员在汽车试验基地对该款新能源汽车做了耗电量试验,发现汽车剩余电量Q()是汽车行驶路程s()的一次函数,试验数据记录如下.
汽车行驶路程s/ 0 50 100 150 200 …
汽车剩余电量Q/ 80 71.5 63 54.5 46 …
(1)根据表中的数据,求Q与s之间的函数表达式;
(2)当汽车剩余电量为39.2 时,若以75的速度匀速行驶,该汽车最多还能行驶多长时间?
17.一辆快递车和一辆轿车先后从甲地出发驶向乙地,到达乙地停止,快递车始终匀速行驶,轿车先以和快递车相同的速度行驶了一段时间后,又提高了速度继续匀速行驶到乙地停止()与快递车行驶的时间x()之间的图象如图所示
(1)快递车的速度为 , ;
(2)在轿车提高速度到乙地的行驶过程中,求轿车距甲地的路程y与x之间的函数关系式,并写出自变量x的取值范围;
(3)当两车在途中相遇时,直接写出两车距乙地的路程.
18.某运输公司派出甲、乙两车负责运送一批货物,已知两车同时从M城出发驶往N城,甲车到达N城后立即按原路返回M城(卸载货物的时间忽略不计),乙车到达N城后停止,如图是甲车、乙车离M城的距离y(千米)与甲车行驶的时间x(小时)的关系,请结合图象回答下列问题:
(1)甲车返回M城的速度为___________千米/小时;
(2)当甲车从N城返回M城的途中与乙车相遇时,相遇处离M城的距离为多少千米?
(3)在甲、乙两车相遇之前,当两车相距10千米时出发时间为何时?
19.小优和小秀家住同一小区,两人同时从小区门口出发到吉林省图书馆查阅资料,小区与图书馆的路程是3600米,小优骑自行车,小秀步行,当小优从小区到图书馆并原路原速返回到小区门口时,小秀刚好到达图书馆,图中折线和线段OD分别表示两人距离小区门口的路程与所经过的时间之间的函数关系.
(1)小优在图书馆查阅资料的时间为______分钟,小秀的速度为______米/分钟;
(2)求线段对应的函数表达式;
(3)当小优与小秀相距不超过时,称为小优与小秀“互相可见”,则小优与小秀“互相可见”持续的时长为______分钟.
20.周末,小明和小亮去植物园,两人同时骑自行车从各自家中沿同一条道路出发,如图中和分别表示小明和小亮距离植物园的路程(千米)与骑行时间(分钟)的关系,请根据图象解答下列问题:
(1)分别求出直线和的函数表达式;
(2)小明出发多长时间追上小亮?此时距离植物园还有多远?
(3)两人在前往植物园的过程中始终保持各自速度不变,请通过计算说明:谁先到达植物园?先到了多长时间?
参考答案
1.解:根据图象可知,收费64元,行程以超过3千米,
设当时,y与x的函数关系式为,
根据题意,得:,
解得,
∴,
当时,,
解得,
(分钟).
故选:D.
2.解:A.根据图象可知,小明骑车的速度为:(千米/小时),故A错误;
B.爸爸中途停留了(分钟),故B错误;
C.(小时),
小时分钟,
即小明在第15分钟追上爸爸,故C正确;
D.根据图象可知,爸爸比小明早到5分钟,故D错误.
故选:C.
3.解:由图象可得,快车的速度为:,
慢车的速度为:,
设快车行驶两车第一次相遇,行驶两车第二次相遇,
则,,
解得,,
∴两车先后两次相遇的间隔时间为,
故选:.
4.解:汽车行驶路程为:,
∴车距天津的路程S(千米)与行驶时间t(时)的函数关系及自变量的取值范围是:.
故选:C.
5.解:①当时,,
∴A、B之间的距离为,结论①正确;
②乙的速度为,
甲的速度为,
,
∴乙行走的速度是甲的1.5倍,结论②正确;
③,,结论③正确;
故结论正确的有①②③.
故选:D.
6.解:设点A、B的坐标为:,
则直线的表达式为:t①,
设直线的表达式为:,
将点B的坐标代入上式得:,
解得:,
则直线的表达式为:②,
联立①②得:,
解得:,两图象交点P的纵坐标为250,
故选:B
7.解:①由图知,汽车单趟行驶了100千米,往返一共行驶了200千米,故①错误;
②汽车在1.5至2小时之间是休息状态没有行驶,故②错误;
③汽车在整个行驶过程中平均速度为(千米/时),故③正确;
④汽车出发后3小时至4.5小时之间,图象为一条直线,
其行驶的速度为匀速,故④错误;
综上所述,正确的为③;
故选:C.
8.解:设
把代入
得
解得
∴
当时,则
解得
故答案为:20
9.解:设甲无人机所在的位置距离地面的高度与无人机上升的时间x之间的为,
当时,,
,解得,
;
设乙无人机所在的位置距离地面的高度与无人机上升的时间x之间的为,
当时,;当时,,
,
解得:,
;
当时,,,
,
时,两架无人机的高度差为,
故答案为:20
10.解:设甲到达B地前的速度是x,到达B地后速度是,乙的速度是y,
,
根据题意可得:,
解得:,
当甲到达B地时,与乙相距1200,
可得:,
解得:,
将代入,
解得:,
所以,
乙相遇时,距离地,
故答案为:1500
11.解:设:段直线解析式为,
把代入中得:,
解得:,
∴,
当时,,
∴点的坐标为:,
设段直线解析式为,
把代入中得:
,解得:,
∴,
∵轿车再休息前行驶300km,休息后按原速度行驶,
∴轿车行驶后300km需,
∴点的坐标为,
设段直线解析式为,
把代入中得:
,解得:,
∴,
∵两车相距150km分两种情况:
①当轿车休息前与货车相距150km时,有:,解得,
②当轿车休息后与货车相距150km时,有:,解得:,
综上所述:两车出发h或h时,两车相距150km.
12.解:由图象可知A村、B村相离,故①正确;
当时,甲、乙相距为,故在此时相遇,故②正确;
当时,设一次函数的解析式为,把,代入得:
,
解得:,
∴一次函数的解析式为,
故甲的速度比乙的速度快,即甲每小时比乙多骑行,故③正确;
当时,函数图象经过点,,
设一次函数的解析式为,代入得:
,
解得:,
,
当时,得,
解得,
;
当时,函数图象经过点,,设一次函数的解析式为,代入得:
,
解得:,
,
当时,得,
解得,
,
综上所述,相遇后,乙又骑行了或时两人相距;
故④正确.
故答案为:①②③④.
13.解:由图象可得,甲的速度为,
乙的速度为,
设乙出发后钟追上甲,则,
解得,
故答案为:.
14.解:①由图像可知甲乙两地相距,故①错误;
②段表示两车相遇后距离逐渐变大,段表示快车到达乙地,慢车去甲地的过程,故②正确;
④慢车的速度为,故④错误;
③快车的速度为,故③正确;
⑤,
∴快车到达乙地后,慢车到达甲地,故⑤正确;
故答案为:②③⑤.
15.(1)解:(1)由图象,得时,,
大连到哈尔滨的路程为900千米,
故答案为:900;
(2)设,
将和代入得,
,
解得:,
关于的函数表达式:;
(3)当油箱中剩余油量为10升时,
(千米),
,
解得:(小时),
当油箱中剩余油量为0升时,
(千米),
,解得:(小时),
,
随的增大而减小,
的取值范围是.
16.(1)解:设Q与s之间的函数表达式为,
根据表中数据可得,,
解得,
Q与s之间的函数表达式为;
(2)解:当时,有,
解得,
汽车以75的速度匀速行驶,
汽车行驶时间为:(),
答:该汽车最多还能行驶.
17.(1)解:快递车的速度为,
∵轿车开始的速度与快递车相同,
∴,
解得.
故答案为:60,;
(2)设轿车距甲地的路程y与x之间的函数关系式为,
把和
,
解得,
∴轿车距甲地的路程y与x之间的函数关系式为;
(3)快递车距甲地的路程y与x之间的函数关系式为,
联立解析式为,
解得,
,
∴当两车在途中相遇时,两车距乙地的路程为.
18.(1)解:根据图像可得当小时时,离M城的距离是90千米,当小时时,离甲地的距离是0千米,
∴甲车返回M城的速度为(千米/小时) .
故答案为:90.
(2)解:设货车离M城的距离y(千米)与甲车行驶时间的函数解析式是,则,解得:,
所以函数解析式是;
设甲车在返回M城过程中离M城的距离y(千米)与甲车行驶时间x(小时)的的解析式是,
则,解得:,
所以函数解析式是,
联立,解得:.
则甲车从N地返回M地的途中与货车相遇时,相遇处到甲地的距离是千米.
(3)解:设两车出发a小时相距10千米,甲到达N地前,解得:;
甲车到达N城后与乙车相遇前:,解得:.
答:在甲、乙两车相遇之前,当两车相距10千米时出发时间或.
19.(1)解:由图象可知,小优在图书馆查阅资料的时间为分钟,
小秀的速度为米/分钟,
故答案为:16,75;
(2)设的解析式为,
将,,代入,
可得:,解得:,
∴线段对应的函数表达式为;
(3)由题意可知,小优的速度为米/分钟,
线段的解析式为,
线段的解析式为,
当小优从小区到图书馆时,即:时,,解得:,
即:小优与小秀“互相可见”持续的时长为分钟;
当小优在图书馆查阅资料时,即:时,当时,两人相距米,当时,两人相距米,故此时不符合题意;
当小优从图书馆回小区时,即:时,,解得:,
即:小优与小秀“互相可见”持续的时长为分钟;
则
综上,小优与小秀“互相可见”持续的时长为分钟,
故答案为:.
20.(1)解:设直线的函数表达式为(、为常数,且).
将和代入,
得,
解得,
∴直线的函数表达式为.
设直线的函数表达式为(、为常数,且).
将和代入,
得,
解得,
∴直线的函数表达式为.
(2)解:当小明追上小亮时,得,
解得,
此时距离植物园为(千米),
∴小明出发50分钟追上小亮,此时距离植物园还有5千米.
(3)解:当小明到达植物园时,得,
解得;
当小亮到达植物园时,得,
解得;
(分钟),
∴小明先到达植物园,先到了25分钟.
一、单选题
1.图中反映某网约车平台收费y(元)与所行驶的路程x(千米)的函数关系,根据图中的信息,当小明通过该网约车从家到机场共收费64元,若车速始终保持60千米/时不变,不考虑其它因素(红绿灯、堵车等),他从家到机场需要( )
A.10分钟 B.15分钟 C.18分钟 D.20分钟
2.小明和爸爸两人从相距4千米的甲地前往乙地,两人同时出发,小明骑自行车,爸爸骑电瓶车.线段,折线分别表示小明和爸爸距离甲地路程S(千米)与时间t(分)之间的函数关系.下列说法正确的是( )
A.小明骑车速度为千米/小时 B.爸爸中途停留了20分钟
C.小明在第15分钟追上爸爸 D.小明比爸爸早到5分钟
3.一辆快车和一辆慢车将一批物资从甲地运往乙地,其中快车送达后立即沿原路返回,且往返速度不变.两车离甲地的距离与慢车行驶时间的函数关系如图所示,那么两车先后两次相遇的间隔时间为( )
A. B. C. D.
4.汽车由天津驶往相距120千米的北京,其平均速度是30千米/时,下图中能表示汽车距北京的距离s(千米)与行驶时间t(小时)之间函数关系的是( )
A. B.
C. D.
5.甲、乙两人分别从A,B两地同时出发,相向而行,匀速前往B地、A地,两人相遇时停留了,又各自按原速前往目的地,甲、乙两人之间的距离与甲所用时间 之间的函数关系如图所示,给出下列结论:
①A,B之间的距离为;
②乙行走的速度是甲的倍;
③,.
其中正确的是( )
A.①② B.①③ C.②③ D.①②③
6.《九章算术》中有这样一道数学题:“今有善行者一百步,不善行者六十步.今不善行者先行一百步,善行者追之.问:几何步及之 ”如图是善行者与不善行者行走的路程S(单位:步)与行走时间t(单位:分)之间的函数图象,则两图象交点P的纵坐标为( )
A.200 B.250 C.300 D.350
7.如图(折线)描述了一辆汽车在某一直路上行驶的过程中,汽车离出发地的距离(千米)与行驶时间(小时)之间的变量关系,根据图中提供的信息,给出下列说法:
①汽车共行驶了100千米;②汽车在1.5至2小时之间匀速行驶;③汽车在整个行驶过程中(含停留过程)的平均速度为千米/时;④汽车出发后3小时至4.5小时之间,其行驶的速度在逐渐减小,其中正确的是( )
A.① B.② C.③ D.④
二、填空题
8.图中反映某网约车平台收费(元)与所行驶的路程(千米)的函数关系,根据图中的信息,当小明通过该网约车从家到机场共收费64元,他家距离机场 千米.
9.甲无人机从地面起飞,乙无人机从距离地面高的楼顶起飞,两架无人机同时匀速上升.甲、乙两架无人机所在的位置距离地面的高度y(单位:m)与无人机上升的时间x(单位:s)之间的关系如图所示.时,两架无人机的高度差为 m.
10.甲、乙两人同时从地出发,以各自的速度匀速向地走去,甲到达后立即以原来速度的1.5倍返回,直到与乙相遇.若甲、乙两人之间的距离(米)与两人行走的时间(分钟)之间的函数图像如图所示,则甲、乙相遇时,距离地 米.
11.货车和轿车分别从甲、乙两地同时出发,沿同一公路相向而行.轿车出发2.4h后休息,直至与货车相遇后,以原速度继续行驶,设两车出发时间为(单位:h),货车、轿车与甲地的距离为(单位:km),(单位:km),图中的线段、折线分别表示,与之间的函数关系.则两车出发 h时,两车相距150km.
12.一条公路旁依次有三个村庄,甲、乙两人骑自行车分别从A村、B村同时出发前往C村,甲、乙之间的距离与骑行时间之间的函数关系如图所示,下列结论:①两村相距;②出发后两人相遇;③甲每小时比乙多骑行;④相遇后,乙又骑行了或时两人相距.其中正确的是 .(填序号)
13.如图,甲、乙两人以相同的路线前往距离单位的培训中心参加学习. 图中分别表示甲、乙两人前往目的地所走的路程(千米) 随时间(分)变化的函数图象,乙出发后 分钟追上甲.
14.如图所示,一列快车从甲地驶往乙地,一列慢车从乙地驶往甲地,两车同时出发,设慢车行驶的时间为,两车之间的距离为,图中的折线表示y与x之间的关系,下列说法中正确的为 .
①甲乙两地相距;②C点表示快车到达乙地;③快车的速度为;④慢车的速度为;⑤快车到达乙地后,慢车到达甲地.
三、解答题
15.2023年,哈尔滨的“冰雪大世界”吸引了众多游客,小明的爸爸将容量为60升的私家车油箱加满后,带着全家从大连自驾到哈尔滨游玩,行驶过程中,车离哈尔滨的路程(千米)与行驶时间(小时)的关系如图所示(中途休息、加油的时间不计).当油箱中剩余油量不超过10升时,车会自动显示加油提醒.设车平均耗油量为0.1升/千米,请根据图象解答下列问题:
(1)直接写出大连到哈尔滨的路程___________千米;
(2)求关于的函数表达式;
(3)当车显示加油提醒后,问行驶时间在怎样的范围内车应进站加油?
16.能源和环境问题是目前全球性急需解决的问题,虽然近百年人类文明有了前所未有的发展,但对于能源的使用和环境的破坏也造成了严重的后果,发展新能源是时代的要求,是未来生存的要求.新能源汽车不仅对环境保护具有重大的意义而且还能够减少对不可再生资源的开发,是全球汽车发展的重要方向.为了解某品牌一款新能源汽车的耗电量,相关技术人员在汽车试验基地对该款新能源汽车做了耗电量试验,发现汽车剩余电量Q()是汽车行驶路程s()的一次函数,试验数据记录如下.
汽车行驶路程s/ 0 50 100 150 200 …
汽车剩余电量Q/ 80 71.5 63 54.5 46 …
(1)根据表中的数据,求Q与s之间的函数表达式;
(2)当汽车剩余电量为39.2 时,若以75的速度匀速行驶,该汽车最多还能行驶多长时间?
17.一辆快递车和一辆轿车先后从甲地出发驶向乙地,到达乙地停止,快递车始终匀速行驶,轿车先以和快递车相同的速度行驶了一段时间后,又提高了速度继续匀速行驶到乙地停止()与快递车行驶的时间x()之间的图象如图所示
(1)快递车的速度为 , ;
(2)在轿车提高速度到乙地的行驶过程中,求轿车距甲地的路程y与x之间的函数关系式,并写出自变量x的取值范围;
(3)当两车在途中相遇时,直接写出两车距乙地的路程.
18.某运输公司派出甲、乙两车负责运送一批货物,已知两车同时从M城出发驶往N城,甲车到达N城后立即按原路返回M城(卸载货物的时间忽略不计),乙车到达N城后停止,如图是甲车、乙车离M城的距离y(千米)与甲车行驶的时间x(小时)的关系,请结合图象回答下列问题:
(1)甲车返回M城的速度为___________千米/小时;
(2)当甲车从N城返回M城的途中与乙车相遇时,相遇处离M城的距离为多少千米?
(3)在甲、乙两车相遇之前,当两车相距10千米时出发时间为何时?
19.小优和小秀家住同一小区,两人同时从小区门口出发到吉林省图书馆查阅资料,小区与图书馆的路程是3600米,小优骑自行车,小秀步行,当小优从小区到图书馆并原路原速返回到小区门口时,小秀刚好到达图书馆,图中折线和线段OD分别表示两人距离小区门口的路程与所经过的时间之间的函数关系.
(1)小优在图书馆查阅资料的时间为______分钟,小秀的速度为______米/分钟;
(2)求线段对应的函数表达式;
(3)当小优与小秀相距不超过时,称为小优与小秀“互相可见”,则小优与小秀“互相可见”持续的时长为______分钟.
20.周末,小明和小亮去植物园,两人同时骑自行车从各自家中沿同一条道路出发,如图中和分别表示小明和小亮距离植物园的路程(千米)与骑行时间(分钟)的关系,请根据图象解答下列问题:
(1)分别求出直线和的函数表达式;
(2)小明出发多长时间追上小亮?此时距离植物园还有多远?
(3)两人在前往植物园的过程中始终保持各自速度不变,请通过计算说明:谁先到达植物园?先到了多长时间?
参考答案
1.解:根据图象可知,收费64元,行程以超过3千米,
设当时,y与x的函数关系式为,
根据题意,得:,
解得,
∴,
当时,,
解得,
(分钟).
故选:D.
2.解:A.根据图象可知,小明骑车的速度为:(千米/小时),故A错误;
B.爸爸中途停留了(分钟),故B错误;
C.(小时),
小时分钟,
即小明在第15分钟追上爸爸,故C正确;
D.根据图象可知,爸爸比小明早到5分钟,故D错误.
故选:C.
3.解:由图象可得,快车的速度为:,
慢车的速度为:,
设快车行驶两车第一次相遇,行驶两车第二次相遇,
则,,
解得,,
∴两车先后两次相遇的间隔时间为,
故选:.
4.解:汽车行驶路程为:,
∴车距天津的路程S(千米)与行驶时间t(时)的函数关系及自变量的取值范围是:.
故选:C.
5.解:①当时,,
∴A、B之间的距离为,结论①正确;
②乙的速度为,
甲的速度为,
,
∴乙行走的速度是甲的1.5倍,结论②正确;
③,,结论③正确;
故结论正确的有①②③.
故选:D.
6.解:设点A、B的坐标为:,
则直线的表达式为:t①,
设直线的表达式为:,
将点B的坐标代入上式得:,
解得:,
则直线的表达式为:②,
联立①②得:,
解得:,两图象交点P的纵坐标为250,
故选:B
7.解:①由图知,汽车单趟行驶了100千米,往返一共行驶了200千米,故①错误;
②汽车在1.5至2小时之间是休息状态没有行驶,故②错误;
③汽车在整个行驶过程中平均速度为(千米/时),故③正确;
④汽车出发后3小时至4.5小时之间,图象为一条直线,
其行驶的速度为匀速,故④错误;
综上所述,正确的为③;
故选:C.
8.解:设
把代入
得
解得
∴
当时,则
解得
故答案为:20
9.解:设甲无人机所在的位置距离地面的高度与无人机上升的时间x之间的为,
当时,,
,解得,
;
设乙无人机所在的位置距离地面的高度与无人机上升的时间x之间的为,
当时,;当时,,
,
解得:,
;
当时,,,
,
时,两架无人机的高度差为,
故答案为:20
10.解:设甲到达B地前的速度是x,到达B地后速度是,乙的速度是y,
,
根据题意可得:,
解得:,
当甲到达B地时,与乙相距1200,
可得:,
解得:,
将代入,
解得:,
所以,
乙相遇时,距离地,
故答案为:1500
11.解:设:段直线解析式为,
把代入中得:,
解得:,
∴,
当时,,
∴点的坐标为:,
设段直线解析式为,
把代入中得:
,解得:,
∴,
∵轿车再休息前行驶300km,休息后按原速度行驶,
∴轿车行驶后300km需,
∴点的坐标为,
设段直线解析式为,
把代入中得:
,解得:,
∴,
∵两车相距150km分两种情况:
①当轿车休息前与货车相距150km时,有:,解得,
②当轿车休息后与货车相距150km时,有:,解得:,
综上所述:两车出发h或h时,两车相距150km.
12.解:由图象可知A村、B村相离,故①正确;
当时,甲、乙相距为,故在此时相遇,故②正确;
当时,设一次函数的解析式为,把,代入得:
,
解得:,
∴一次函数的解析式为,
故甲的速度比乙的速度快,即甲每小时比乙多骑行,故③正确;
当时,函数图象经过点,,
设一次函数的解析式为,代入得:
,
解得:,
,
当时,得,
解得,
;
当时,函数图象经过点,,设一次函数的解析式为,代入得:
,
解得:,
,
当时,得,
解得,
,
综上所述,相遇后,乙又骑行了或时两人相距;
故④正确.
故答案为:①②③④.
13.解:由图象可得,甲的速度为,
乙的速度为,
设乙出发后钟追上甲,则,
解得,
故答案为:.
14.解:①由图像可知甲乙两地相距,故①错误;
②段表示两车相遇后距离逐渐变大,段表示快车到达乙地,慢车去甲地的过程,故②正确;
④慢车的速度为,故④错误;
③快车的速度为,故③正确;
⑤,
∴快车到达乙地后,慢车到达甲地,故⑤正确;
故答案为:②③⑤.
15.(1)解:(1)由图象,得时,,
大连到哈尔滨的路程为900千米,
故答案为:900;
(2)设,
将和代入得,
,
解得:,
关于的函数表达式:;
(3)当油箱中剩余油量为10升时,
(千米),
,
解得:(小时),
当油箱中剩余油量为0升时,
(千米),
,解得:(小时),
,
随的增大而减小,
的取值范围是.
16.(1)解:设Q与s之间的函数表达式为,
根据表中数据可得,,
解得,
Q与s之间的函数表达式为;
(2)解:当时,有,
解得,
汽车以75的速度匀速行驶,
汽车行驶时间为:(),
答:该汽车最多还能行驶.
17.(1)解:快递车的速度为,
∵轿车开始的速度与快递车相同,
∴,
解得.
故答案为:60,;
(2)设轿车距甲地的路程y与x之间的函数关系式为,
把和
,
解得,
∴轿车距甲地的路程y与x之间的函数关系式为;
(3)快递车距甲地的路程y与x之间的函数关系式为,
联立解析式为,
解得,
,
∴当两车在途中相遇时,两车距乙地的路程为.
18.(1)解:根据图像可得当小时时,离M城的距离是90千米,当小时时,离甲地的距离是0千米,
∴甲车返回M城的速度为(千米/小时) .
故答案为:90.
(2)解:设货车离M城的距离y(千米)与甲车行驶时间的函数解析式是,则,解得:,
所以函数解析式是;
设甲车在返回M城过程中离M城的距离y(千米)与甲车行驶时间x(小时)的的解析式是,
则,解得:,
所以函数解析式是,
联立,解得:.
则甲车从N地返回M地的途中与货车相遇时,相遇处到甲地的距离是千米.
(3)解:设两车出发a小时相距10千米,甲到达N地前,解得:;
甲车到达N城后与乙车相遇前:,解得:.
答:在甲、乙两车相遇之前,当两车相距10千米时出发时间或.
19.(1)解:由图象可知,小优在图书馆查阅资料的时间为分钟,
小秀的速度为米/分钟,
故答案为:16,75;
(2)设的解析式为,
将,,代入,
可得:,解得:,
∴线段对应的函数表达式为;
(3)由题意可知,小优的速度为米/分钟,
线段的解析式为,
线段的解析式为,
当小优从小区到图书馆时,即:时,,解得:,
即:小优与小秀“互相可见”持续的时长为分钟;
当小优在图书馆查阅资料时,即:时,当时,两人相距米,当时,两人相距米,故此时不符合题意;
当小优从图书馆回小区时,即:时,,解得:,
即:小优与小秀“互相可见”持续的时长为分钟;
则
综上,小优与小秀“互相可见”持续的时长为分钟,
故答案为:.
20.(1)解:设直线的函数表达式为(、为常数,且).
将和代入,
得,
解得,
∴直线的函数表达式为.
设直线的函数表达式为(、为常数,且).
将和代入,
得,
解得,
∴直线的函数表达式为.
(2)解:当小明追上小亮时,得,
解得,
此时距离植物园为(千米),
∴小明出发50分钟追上小亮,此时距离植物园还有5千米.
(3)解:当小明到达植物园时,得,
解得;
当小亮到达植物园时,得,
解得;
(分钟),
∴小明先到达植物园,先到了25分钟.
