2023~2024学年苏科版数学七年级下册期中复习专题讲义(7.5-多边形的内角和与外角和)(无答案)
文档属性
| 名称 | 2023~2024学年苏科版数学七年级下册期中复习专题讲义(7.5-多边形的内角和与外角和)(无答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 359.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-04-18 00:00:00 | ||
图片预览



文档简介
2023-2024学年苏科版数学七年级下册期中复习专题讲义
(专题5-多边形的内角和与外角和)
【考点一】三角形的内角和
【知识梳理】 三角形的内角和是180°. 当已知三角形两个内角的度数或两个内角的度数和时,利用它可求第三个内角的度数,当已知三个内角间的一些数量关系时,也可利用它列方程求各个角的度数. 2. 直角三角形两个锐角和是90°,即直角三角形的两个锐角互余; 3. 三角形的三个内角中,至少有两个锐角,最多有一个钝角或直角,三角形中最大内角不小于60°. 【典型例题】 1.在△ABC中,若∠A=40°,∠B=35°,则△ABC是( ) A.直角三角形 B.钝角三角形 C.锐角三角形 D.等边三角形 2.直角三角形的一锐角是50°,那么另一锐角是( ) A.40° B.50° C.60° D.70° 3.在下列条件中:①,②,③,④中,能确定是直角三角形的条件有 A.1个 B.2个 C.3个 D.4个 4.如图,已知AD和AE分别是△ABC的高线和角平分线,若∠B=56°,∠EAD=10°,则∠C的度数为( ) A.80° B.76° C.74° D.66° 5.如图,将纸片沿折叠,使点落在点处,且平分,平分,若,则的度数为 A. B. C. D. 6.如图,△ABC中,∠B=40°,∠BAC=90°,CD平分∠ACB,AD∥BC,则∠D的度数为 . 7.如图,在△ABC中,AD是△ABC的角平分线,F在射线AD上,FE⊥BC于E,∠C=80°,∠B=36°,则∠F= 度. 8.如图,在△ABC中,AD是高,AE、BF是角平分线,它们相交于点O,∠C=70°. (1)∠AOB的度数为 ; (2)若∠ABC=60°,求∠DAE的度数.
【考点二】多边形的内角和
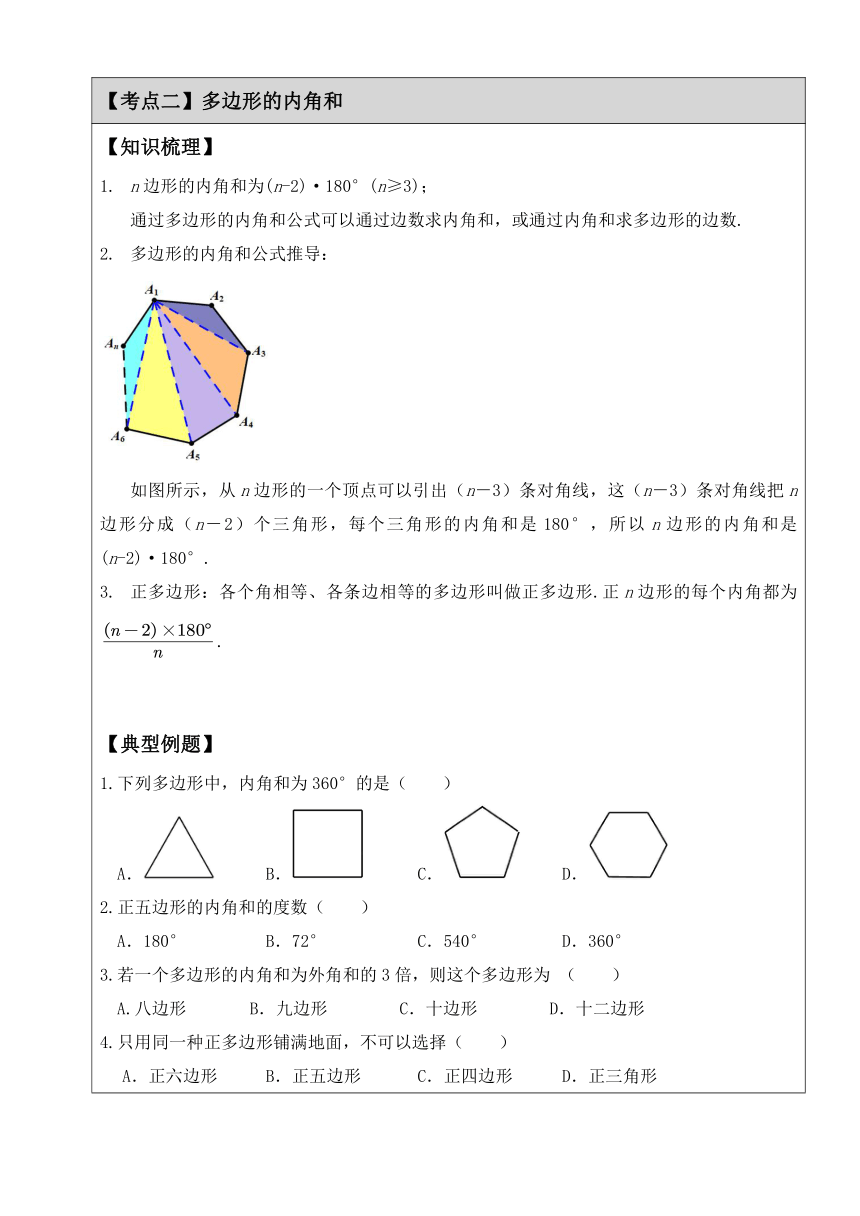
【知识梳理】 1. n边形的内角和为(n-2)·180°(n≥3); 通过多边形的内角和公式可以通过边数求内角和,或通过内角和求多边形的边数. 2. 多边形的内角和公式推导: 如图所示,从n边形的一个顶点可以引出(n-3)条对角线,这(n-3)条对角线把n边形分成(n-2)个三角形,每个三角形的内角和是180°,所以n边形的内角和是(n-2)·180°. 3. 正多边形:各个角相等、各条边相等的多边形叫做正多边形.正n边形的每个内角都为. 【典型例题】 1.下列多边形中,内角和为360°的是( ) A. B. C. D. 2.正五边形的内角和的度数( ) A.180° B.72° C.540° D.360° 3.若一个多边形的内角和为外角和的3倍,则这个多边形为 ( ) A.八边形 B.九边形 C.十边形 D.十二边形 4.只用同一种正多边形铺满地面,不可以选择( ) A.正六边形 B.正五边形 C.正四边形 D.正三角形 5.在一个多边形中,小于108°的内角最多有( )个. A.2 B.3 C.4 D.5 6.如图,已知,设,,则( ) A. B. C. D. 7.已知一个多边形的内角和比外角和多900°,并且这个多边形各个内角的度数都相等.这个多边形的每个内角是多少度? 8.如图是一个凹多边形,∠A=90°,∠C=106°,∠D=116°,∠E=100°;求∠1+∠2的值.
【考点三】多边形的外角和
【知识梳理】 1. 多边形的外角:多边形的一边与它的邻边的延长线组成的角,叫做多边形的外角. 2. 多边形的外角和:在多边形的每个顶点处分别取一个外角,这些外角的和叫做多边形的外角和,多边形的外角和恒等于360°,与边数的多少没有关系. 如图所示:∠1+∠2+∠3+∠4+∠5就是五边形ABCDE的外角和,为360°. 3. 正n边形的每个内角都相等,所以它的每个外角都相等,都等于. 4. 多边形的外角和的推导:多边形的每个内角加上与它相邻的外角都等于180°,所以n边形的外角和等于n个180°的平角减去多边形的内角和,即. 【典型例题】 1.一个多边形的每个外角都是,则这个多边形的边数为 A.八 B.九 C.十 D.七 2.一个多边形的每一个外角都为40°,那么这个多边形的内角和为( ) A.360° B.1080° C.1260° D.1620° 3.如图,四边形中,,,,则的度数为 A. B. C. D. 4.如图,在五边形ABCDE中,AB∥ED,∠1,∠2,∠3分别是∠ABC,∠BCD,∠CDE的外角,则∠1+∠2+∠3的度数为( ) A.180° B.210° C.240° D.270° 5.如图,在七边形中,和都是它的外角,且,则的结果为( ) A. B. C. D. 6.如图,在五边形ABCDE中,∠A=35°,去掉∠A后得到一个六边形BCDENM,则∠1+∠2的度数为 . 7.若一个多边形的外角和是其内角和的,则这个多边形是 边形. 8.如图,贾玲从点出发,前进5米后向右转,再前进5米后又向右转,这样一直下去,直到她第一次回到出发点为止,她所走的路径构成了一个多边形. (1)贾玲一共走了多少米? (2)求这个多边形的内角和.
【考点四】不规则图形的内角和与外角和
【典型例题】 1.如图.∠A+∠B+∠C+∠D+∠E的度数为( ) A.90° B.180° C.120° D.360° 2小明一笔画成了如图所示的图形,则的度数为( ) A. B. C. D. 3.如图,求∠A+∠B+∠C+∠D+∠E+∠F+∠G+∠H的度数等于( ) A.180° B.360° C.540° D.720° 4.如图所示,则∠A+∠B+∠C+∠D+∠E+∠F的度数是( ) A.180° B.270° C.360° D.540° 5.如图,∠A+∠B+∠C+∠D+∠E+∠F+∠G+∠H= . 6.如图1所示,△ABO与△CDO称为对角“三角形”,其中∠A+∠B=∠C+∠D,利用这个结论,在图2中,求∠A+∠B+∠C+∠D+∠E+∠F∠G= . 7.已知:如图所示的图形中,有6个顶角分别是,,,,,.求证:. 8.已知如图,求:∠A+∠B+∠C+∠D+∠E+∠F+∠G的度数。
(专题5-多边形的内角和与外角和)
【考点一】三角形的内角和
【知识梳理】 三角形的内角和是180°. 当已知三角形两个内角的度数或两个内角的度数和时,利用它可求第三个内角的度数,当已知三个内角间的一些数量关系时,也可利用它列方程求各个角的度数. 2. 直角三角形两个锐角和是90°,即直角三角形的两个锐角互余; 3. 三角形的三个内角中,至少有两个锐角,最多有一个钝角或直角,三角形中最大内角不小于60°. 【典型例题】 1.在△ABC中,若∠A=40°,∠B=35°,则△ABC是( ) A.直角三角形 B.钝角三角形 C.锐角三角形 D.等边三角形 2.直角三角形的一锐角是50°,那么另一锐角是( ) A.40° B.50° C.60° D.70° 3.在下列条件中:①,②,③,④中,能确定是直角三角形的条件有 A.1个 B.2个 C.3个 D.4个 4.如图,已知AD和AE分别是△ABC的高线和角平分线,若∠B=56°,∠EAD=10°,则∠C的度数为( ) A.80° B.76° C.74° D.66° 5.如图,将纸片沿折叠,使点落在点处,且平分,平分,若,则的度数为 A. B. C. D. 6.如图,△ABC中,∠B=40°,∠BAC=90°,CD平分∠ACB,AD∥BC,则∠D的度数为 . 7.如图,在△ABC中,AD是△ABC的角平分线,F在射线AD上,FE⊥BC于E,∠C=80°,∠B=36°,则∠F= 度. 8.如图,在△ABC中,AD是高,AE、BF是角平分线,它们相交于点O,∠C=70°. (1)∠AOB的度数为 ; (2)若∠ABC=60°,求∠DAE的度数.
【考点二】多边形的内角和
【知识梳理】 1. n边形的内角和为(n-2)·180°(n≥3); 通过多边形的内角和公式可以通过边数求内角和,或通过内角和求多边形的边数. 2. 多边形的内角和公式推导: 如图所示,从n边形的一个顶点可以引出(n-3)条对角线,这(n-3)条对角线把n边形分成(n-2)个三角形,每个三角形的内角和是180°,所以n边形的内角和是(n-2)·180°. 3. 正多边形:各个角相等、各条边相等的多边形叫做正多边形.正n边形的每个内角都为. 【典型例题】 1.下列多边形中,内角和为360°的是( ) A. B. C. D. 2.正五边形的内角和的度数( ) A.180° B.72° C.540° D.360° 3.若一个多边形的内角和为外角和的3倍,则这个多边形为 ( ) A.八边形 B.九边形 C.十边形 D.十二边形 4.只用同一种正多边形铺满地面,不可以选择( ) A.正六边形 B.正五边形 C.正四边形 D.正三角形 5.在一个多边形中,小于108°的内角最多有( )个. A.2 B.3 C.4 D.5 6.如图,已知,设,,则( ) A. B. C. D. 7.已知一个多边形的内角和比外角和多900°,并且这个多边形各个内角的度数都相等.这个多边形的每个内角是多少度? 8.如图是一个凹多边形,∠A=90°,∠C=106°,∠D=116°,∠E=100°;求∠1+∠2的值.
【考点三】多边形的外角和
【知识梳理】 1. 多边形的外角:多边形的一边与它的邻边的延长线组成的角,叫做多边形的外角. 2. 多边形的外角和:在多边形的每个顶点处分别取一个外角,这些外角的和叫做多边形的外角和,多边形的外角和恒等于360°,与边数的多少没有关系. 如图所示:∠1+∠2+∠3+∠4+∠5就是五边形ABCDE的外角和,为360°. 3. 正n边形的每个内角都相等,所以它的每个外角都相等,都等于. 4. 多边形的外角和的推导:多边形的每个内角加上与它相邻的外角都等于180°,所以n边形的外角和等于n个180°的平角减去多边形的内角和,即. 【典型例题】 1.一个多边形的每个外角都是,则这个多边形的边数为 A.八 B.九 C.十 D.七 2.一个多边形的每一个外角都为40°,那么这个多边形的内角和为( ) A.360° B.1080° C.1260° D.1620° 3.如图,四边形中,,,,则的度数为 A. B. C. D. 4.如图,在五边形ABCDE中,AB∥ED,∠1,∠2,∠3分别是∠ABC,∠BCD,∠CDE的外角,则∠1+∠2+∠3的度数为( ) A.180° B.210° C.240° D.270° 5.如图,在七边形中,和都是它的外角,且,则的结果为( ) A. B. C. D. 6.如图,在五边形ABCDE中,∠A=35°,去掉∠A后得到一个六边形BCDENM,则∠1+∠2的度数为 . 7.若一个多边形的外角和是其内角和的,则这个多边形是 边形. 8.如图,贾玲从点出发,前进5米后向右转,再前进5米后又向右转,这样一直下去,直到她第一次回到出发点为止,她所走的路径构成了一个多边形. (1)贾玲一共走了多少米? (2)求这个多边形的内角和.
【考点四】不规则图形的内角和与外角和
【典型例题】 1.如图.∠A+∠B+∠C+∠D+∠E的度数为( ) A.90° B.180° C.120° D.360° 2小明一笔画成了如图所示的图形,则的度数为( ) A. B. C. D. 3.如图,求∠A+∠B+∠C+∠D+∠E+∠F+∠G+∠H的度数等于( ) A.180° B.360° C.540° D.720° 4.如图所示,则∠A+∠B+∠C+∠D+∠E+∠F的度数是( ) A.180° B.270° C.360° D.540° 5.如图,∠A+∠B+∠C+∠D+∠E+∠F+∠G+∠H= . 6.如图1所示,△ABO与△CDO称为对角“三角形”,其中∠A+∠B=∠C+∠D,利用这个结论,在图2中,求∠A+∠B+∠C+∠D+∠E+∠F∠G= . 7.已知:如图所示的图形中,有6个顶角分别是,,,,,.求证:. 8.已知如图,求:∠A+∠B+∠C+∠D+∠E+∠F+∠G的度数。
同课章节目录
- 第7章 平面图形的认识(二)
- 7.1 探索直线平行的条件
- 7.2 探索平行线的性质
- 7.3 图形的平移
- 7.4 认识三角形
- 7.5 多边形的内角和与外角和
- 第8章 幂的运算
- 8.1 同底数幂的乘法
- 8.2 幂的乘方与积的乘方
- 8.3 同底数幂的除法
- 第9章 整式乘法与因式分解
- 9.1 单项式乘单项式
- 9.2 单项式乘多项式
- 9.3 多项式乘多项式
- 9.4 乘法公式
- 9.5 多项式的因式分解
- 第10章 二元一次方程组
- 10.1 二元一次方程
- 10.2 二元一次方程组
- 10.3 解二元一次方程组
- 10.4 三元一次方程组
- 10.5 用二元一次方程解决问题
- 第11章 一元一次不等式
- 11.1 生活中的不等式
- 11.2 不等式的解集
- 11.3 不等式的性质
- 11.4 解一元一次不等式
- 11.5 用一元一次不等式解决问题
- 11.6 一元一次不等式组
- 第12章 证明
- 12.1 定义与命题
- 12.2 证明
- 12.3 互逆命题
