两角和差的三角函数
图片预览








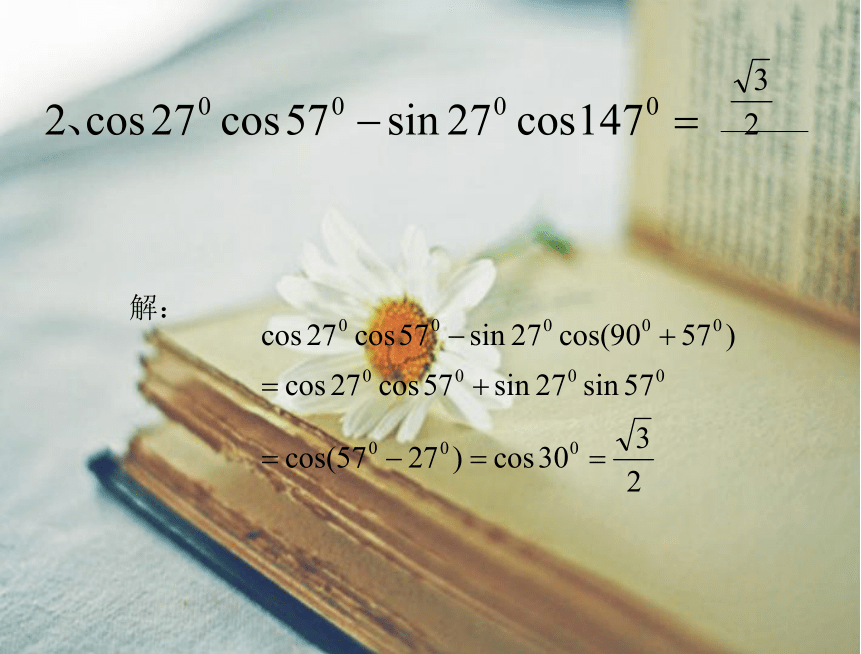



文档简介
课件30张PPT。第 5 讲两角和与差及二倍角的三角函数公式 已知两个非零向量a与b,它们的夹角为θ,则数量|a||b|cosθ
叫做 a 与 b 的数量积(或内积),记作 a·b,即 a·b=|a||b|cosθ.规定
零向量与任一向量的数量积为 0,即 0·a=0.1、两个向量的数量积的定义 2、任意角的三角函数的定义
设α是一个任意角,角α的终边上任意一点 P(x,y),它与原
点的距离是 r(r>0),那么如图:点A,B的坐标分别可记为(cos ,sin ),(cos ,sin )的夹角为根据向量的数量积的定义得:cos(α+β)=1.两角和与差的三角函数cosαcosβ-sinαsinβCα+β:cos(α+β)=______________________;
Cα-β:cos(α-β)=cosαcosβ+sinαsinβ;
Sα+β:sin(α+β)=sinαcosβ+cosαsinβ;
Sα-β:sin(α-β)=sinαcosβ-cosαsinβ;Tα+β:tan(α+β)=___________________; tanα+tanβ
1-tanαtanβ公式要牢记2.二倍角的三角函数S2α:sin2α=____________;2sinαcosα1-2sin2αC2α:cos2α=cos2α-sin2α=2cos2α-1=__________;解:———考点:1给值求角问题cos(α+β) D同步练习解:4.已知α为第二象限角,sinα= ,则 tan2α=____.2 .(2014 年上海) 函数 y =1 -2cos2(2x) 的最小正周期是________.3.已知角α的终边过点(3,-4),则 cos2α=_______.3
5考点:2给角求值问题例 1:化简求值:(1)tan15°;课时2:
【规律方法】三角函数的给角求值,关键是把待求角用已
知角表示:
①已知角为两个时,待求角一般表示为已知角的和或差;
②已知角为一个时,待求角一般与已知角成“倍的关系”
或“互余、互补”的关系.【互动探究】考点3给值求值问题 ●难点突破●
⊙三角函数公式的综合应用
叫做 a 与 b 的数量积(或内积),记作 a·b,即 a·b=|a||b|cosθ.规定
零向量与任一向量的数量积为 0,即 0·a=0.1、两个向量的数量积的定义 2、任意角的三角函数的定义
设α是一个任意角,角α的终边上任意一点 P(x,y),它与原
点的距离是 r(r>0),那么如图:点A,B的坐标分别可记为(cos ,sin ),(cos ,sin )的夹角为根据向量的数量积的定义得:cos(α+β)=1.两角和与差的三角函数cosαcosβ-sinαsinβCα+β:cos(α+β)=______________________;
Cα-β:cos(α-β)=cosαcosβ+sinαsinβ;
Sα+β:sin(α+β)=sinαcosβ+cosαsinβ;
Sα-β:sin(α-β)=sinαcosβ-cosαsinβ;Tα+β:tan(α+β)=___________________; tanα+tanβ
1-tanαtanβ公式要牢记2.二倍角的三角函数S2α:sin2α=____________;2sinαcosα1-2sin2αC2α:cos2α=cos2α-sin2α=2cos2α-1=__________;解:———考点:1给值求角问题cos(α+β) D同步练习解:4.已知α为第二象限角,sinα= ,则 tan2α=____.2 .(2014 年上海) 函数 y =1 -2cos2(2x) 的最小正周期是________.3.已知角α的终边过点(3,-4),则 cos2α=_______.3
5考点:2给角求值问题例 1:化简求值:(1)tan15°;课时2:
【规律方法】三角函数的给角求值,关键是把待求角用已
知角表示:
①已知角为两个时,待求角一般表示为已知角的和或差;
②已知角为一个时,待求角一般与已知角成“倍的关系”
或“互余、互补”的关系.【互动探究】考点3给值求值问题 ●难点突破●
⊙三角函数公式的综合应用
