5.4 平移同步练习(含解析)
图片预览



文档简介
中小学教育资源及组卷应用平台
人教版七年级下册数学5.1.1相交线 同步练习
选择题(本大题共10小题,每小题3分,共30分。下列各题的备选答案中,只有一项是最符合题意的,请选出。)
1.如图所示,△FDE经过怎样的平移可得到△ABC
A.沿射线EC的方向移动DB长
B.沿射线CE的方向移动DB长
C.沿射线EC的方向移动CD长
D.沿射线BD的方向移动BD长
2.将长度为5cm的线段向上平移10cm所得线段长度是
A.10cm B.5cm
C.0cm D.无法确定
3.下列现象不包含平移的是
A.飞机起飞前在跑道上加速滑行
B.汽车在笔直的公路上行驶
C.游乐场的过山车在翻筋斗
D.起重机将重物由地面竖直吊起到一定高度
3.下列现象不包含平移的是
A.飞机起飞前在跑道上加速滑行
B.汽车在笔直的公路上行驶
C.游乐场的过山车在翻筋斗
D.起重机将重物由地面竖直吊起到一定高度
5.如图,将直线l1沿从A到B的方向平移得到l2,若∠1=40°,则∠2=
A.40° B.50°
C.90° D.140°
6.如图,直线∥,∠1=70°,∠2=30°,则∠A的度数是( )
A.30° B.35° C. 40° D. 50°
7.如图所示,直线l1∥l2,点A、B在直线l2上,点C、D在直线l1上,若△ABC的面积为S1,△ABD的面积为S2,则( )
S1>S2 B.S1=S2 C.S1<S2 D.不确定
8.下列说法:①两直线平行,同旁内角互补;②内错角相等,两直线平行;③同位角相等,两直线平行;④垂直于同一条直线的两条直线平行,其中是平行线的性质的是 ( )
A.① B.②和③ C.④ D.①和④
9.如图所示,AB∥CD,若∠2是∠1的2倍,则∠2等于 ( )
A.60° B.90° C.120° D.150°
10.下列图形中,由AB∥CD,能得到∠1=∠2的是( )
填空题(本大题共5小题,每小题4分,共20分。)
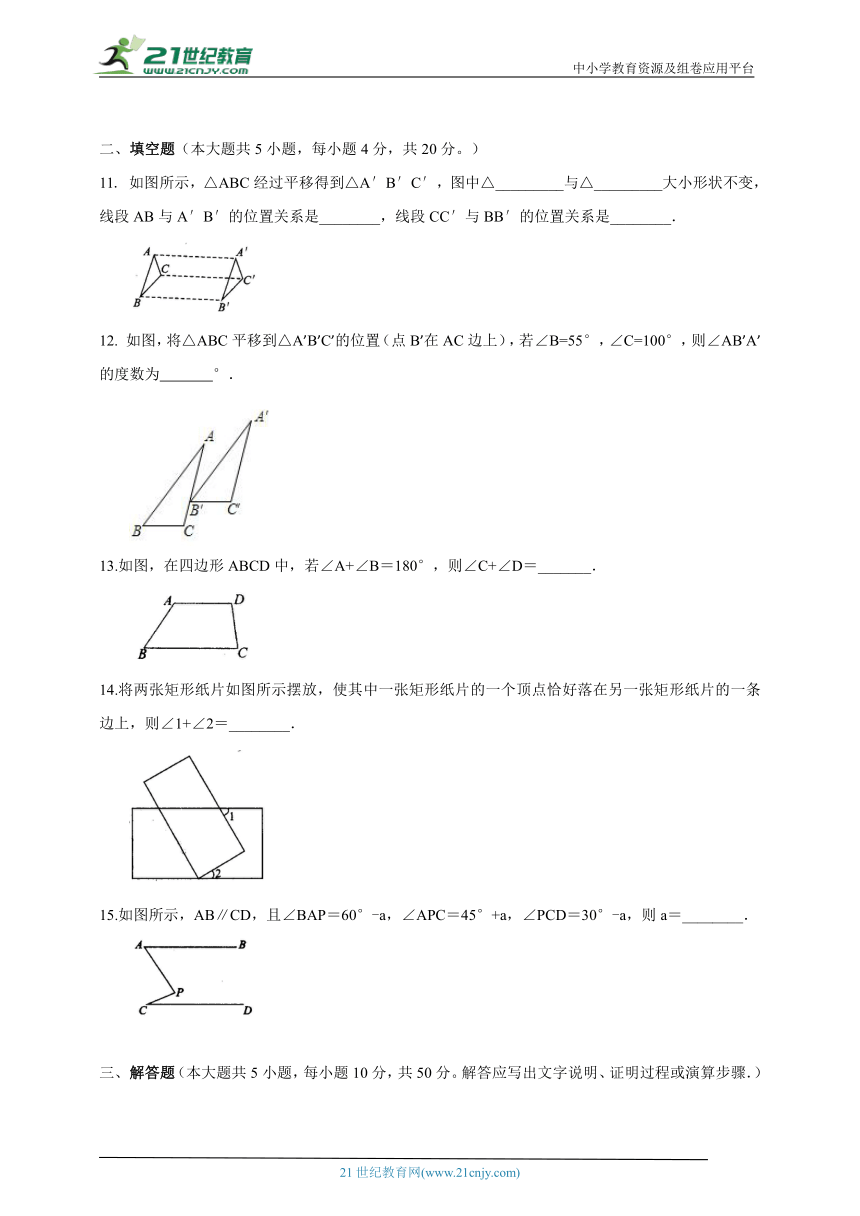
11. 如图所示,△ABC经过平移得到△A′B′C′,图中△_________与△_________大小形状不变,线段AB与A′B′的位置关系是________,线段CC′与BB′的位置关系是________.
12. 如图,将△ABC平移到△A’B’C’的位置(点B’在AC边上),若∠B=55°,∠C=100°,则∠AB’A’的度数为 °.
13.如图,在四边形ABCD中,若∠A+∠B=180°,则∠C+∠D=_______.
14.将两张矩形纸片如图所示摆放,使其中一张矩形纸片的一个顶点恰好落在另一张矩形纸片的一条边上,则∠1+∠2=________.
15.如图所示,AB∥CD,且∠BAP=60°-a,∠APC=45°+a,∠PCD=30°-a,则a=________.
解答题(本大题共5小题,每小题10分,共50分。解答应写出文字说明、证明过程或演算步骤.)
16.如图,直线AB∥CD,BC平分∠ABD,∠1=65°,求∠2的度数.
17.如图,a∥b∥c,∠1=60°,∠2=36°,AP平分∠BAC,求∠PAQ的度数.
18.给出下列语句,先判断是否为命题,如果是命题请指明其题设和结论.
(1)同旁内角互补,两直线平行;
(2)直角都相等;
(3)画直线AB;
(4)凡内错角都相等.
19. 如图,将四边形ABCD平移到四边形EFGH的位置,根据平移后对应点所连的线段平行且相等,写出图中平行的线段和相等的线段.
20.如图,凯瑞酒店准备进行装修,把楼梯铺上地毯,已知楼梯的宽度是2米,楼梯的总长度为8米,总高度为6米,已知这种地毯每平方米的售价是60元.请你帮助酒店老板算下,购买地毯至少需要多少元?
参考答案
选择题
1.【答案】A
2.【答案】B
【解析】平移不改变图形的大小和形状.故线段长度不变,仍为5cm.
3.【答案】C
【解析】A.飞机起飞前在跑道上加速滑行,是平移.
B.汽车在笔直的公路上行驶,车身的移动是平移.
C.游乐场的过山车在翻筋斗,不是平移,是旋转.
D.起重机将重物由地面竖直吊起到一定高度,是平移.
故选C.
4.【答案】C
5.【答案】A
6.【解析】∵将直线l1沿AB的方向平移得到l2,∴l1∥l2,∵∠1=40°,∴∠2=40°,故选
【答案】C.
【解析】
解:∵直线∥,∠1=70°,
∴∠3=∠1=70°,
∵∠2+∠A=∠3,
∴∠A=∠3﹣∠2=70°﹣30°=40°.
7.【答案】B
【解析】因为l1∥l2,所以C、D两点到l2的距离相等.同时△ABC和△ABD有共同的底AB,所以它们的面积相等.
8.【答案】A;
【解析】两直线平行角的关系.
9.【答案】C;
【解析】∠2+∠1=180°,又∠2=2∠1,所以∠2=120°.
10.【答案】B;
【解析】∠2与∠1的对顶角是同位角的关系.
二、填空题
11.【答案】ABC, A′B′C′,平行,平行;
【解析】平移的性质.
12.【答案】25.
【解析】由∠B=55°,∠C=100°,推出∠A=180°-∠B-∠C=25°,由平移得到
AB∥A’B’,由平行性质可得∠AB’A’=∠A=25°.
13.【答案】180°;
【解析】由已知可得:AD∥BC,由平行的性质可得:∠D+∠C=180°.
14.【答案】90°;
15.【答案】15°;
【解析】由图可知:∠APC=∠BAP+∠PCD,即有45°+a=60°-a+30°-a,
解得:a=15°.
四、解答题
16.【解析】
解:∵AB∥CD,
∴∠ABC=∠1=65°,∠ABD+∠BDC=180°,
∵BC平分∠ABD,
∴∠ABD=2∠ABC=130°,
∴∠BDC=180°﹣∠ABD=50°,
∴∠2=∠BDC=50°.
17【解析】
解:∵a∥b∥c,
∴∠BAQ=∠1=60°,∠CAQ=∠2=36°,∠BAC=60°+36°=96°,
又AP平分∠BAC,∠BAP=×96°=48°,
∴∠PAQ=∠BAQ-∠BAP=60°-48°=12°.
18.【解析】
解: (3)不是命题,(1)、(2)、(4)是命题,题设和结论见下表.
19.【解析】
解:平行的线段:AE∥CG∥DH,AE∥BF∥DH,相等的线段:AE=BF=CG=DH.
20.【解析】
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
人教版七年级下册数学5.1.1相交线 同步练习
选择题(本大题共10小题,每小题3分,共30分。下列各题的备选答案中,只有一项是最符合题意的,请选出。)
1.如图所示,△FDE经过怎样的平移可得到△ABC
A.沿射线EC的方向移动DB长
B.沿射线CE的方向移动DB长
C.沿射线EC的方向移动CD长
D.沿射线BD的方向移动BD长
2.将长度为5cm的线段向上平移10cm所得线段长度是
A.10cm B.5cm
C.0cm D.无法确定
3.下列现象不包含平移的是
A.飞机起飞前在跑道上加速滑行
B.汽车在笔直的公路上行驶
C.游乐场的过山车在翻筋斗
D.起重机将重物由地面竖直吊起到一定高度
3.下列现象不包含平移的是
A.飞机起飞前在跑道上加速滑行
B.汽车在笔直的公路上行驶
C.游乐场的过山车在翻筋斗
D.起重机将重物由地面竖直吊起到一定高度
5.如图,将直线l1沿从A到B的方向平移得到l2,若∠1=40°,则∠2=
A.40° B.50°
C.90° D.140°
6.如图,直线∥,∠1=70°,∠2=30°,则∠A的度数是( )
A.30° B.35° C. 40° D. 50°
7.如图所示,直线l1∥l2,点A、B在直线l2上,点C、D在直线l1上,若△ABC的面积为S1,△ABD的面积为S2,则( )
S1>S2 B.S1=S2 C.S1<S2 D.不确定
8.下列说法:①两直线平行,同旁内角互补;②内错角相等,两直线平行;③同位角相等,两直线平行;④垂直于同一条直线的两条直线平行,其中是平行线的性质的是 ( )
A.① B.②和③ C.④ D.①和④
9.如图所示,AB∥CD,若∠2是∠1的2倍,则∠2等于 ( )
A.60° B.90° C.120° D.150°
10.下列图形中,由AB∥CD,能得到∠1=∠2的是( )
填空题(本大题共5小题,每小题4分,共20分。)
11. 如图所示,△ABC经过平移得到△A′B′C′,图中△_________与△_________大小形状不变,线段AB与A′B′的位置关系是________,线段CC′与BB′的位置关系是________.
12. 如图,将△ABC平移到△A’B’C’的位置(点B’在AC边上),若∠B=55°,∠C=100°,则∠AB’A’的度数为 °.
13.如图,在四边形ABCD中,若∠A+∠B=180°,则∠C+∠D=_______.
14.将两张矩形纸片如图所示摆放,使其中一张矩形纸片的一个顶点恰好落在另一张矩形纸片的一条边上,则∠1+∠2=________.
15.如图所示,AB∥CD,且∠BAP=60°-a,∠APC=45°+a,∠PCD=30°-a,则a=________.
解答题(本大题共5小题,每小题10分,共50分。解答应写出文字说明、证明过程或演算步骤.)
16.如图,直线AB∥CD,BC平分∠ABD,∠1=65°,求∠2的度数.
17.如图,a∥b∥c,∠1=60°,∠2=36°,AP平分∠BAC,求∠PAQ的度数.
18.给出下列语句,先判断是否为命题,如果是命题请指明其题设和结论.
(1)同旁内角互补,两直线平行;
(2)直角都相等;
(3)画直线AB;
(4)凡内错角都相等.
19. 如图,将四边形ABCD平移到四边形EFGH的位置,根据平移后对应点所连的线段平行且相等,写出图中平行的线段和相等的线段.
20.如图,凯瑞酒店准备进行装修,把楼梯铺上地毯,已知楼梯的宽度是2米,楼梯的总长度为8米,总高度为6米,已知这种地毯每平方米的售价是60元.请你帮助酒店老板算下,购买地毯至少需要多少元?
参考答案
选择题
1.【答案】A
2.【答案】B
【解析】平移不改变图形的大小和形状.故线段长度不变,仍为5cm.
3.【答案】C
【解析】A.飞机起飞前在跑道上加速滑行,是平移.
B.汽车在笔直的公路上行驶,车身的移动是平移.
C.游乐场的过山车在翻筋斗,不是平移,是旋转.
D.起重机将重物由地面竖直吊起到一定高度,是平移.
故选C.
4.【答案】C
5.【答案】A
6.【解析】∵将直线l1沿AB的方向平移得到l2,∴l1∥l2,∵∠1=40°,∴∠2=40°,故选
【答案】C.
【解析】
解:∵直线∥,∠1=70°,
∴∠3=∠1=70°,
∵∠2+∠A=∠3,
∴∠A=∠3﹣∠2=70°﹣30°=40°.
7.【答案】B
【解析】因为l1∥l2,所以C、D两点到l2的距离相等.同时△ABC和△ABD有共同的底AB,所以它们的面积相等.
8.【答案】A;
【解析】两直线平行角的关系.
9.【答案】C;
【解析】∠2+∠1=180°,又∠2=2∠1,所以∠2=120°.
10.【答案】B;
【解析】∠2与∠1的对顶角是同位角的关系.
二、填空题
11.【答案】ABC, A′B′C′,平行,平行;
【解析】平移的性质.
12.【答案】25.
【解析】由∠B=55°,∠C=100°,推出∠A=180°-∠B-∠C=25°,由平移得到
AB∥A’B’,由平行性质可得∠AB’A’=∠A=25°.
13.【答案】180°;
【解析】由已知可得:AD∥BC,由平行的性质可得:∠D+∠C=180°.
14.【答案】90°;
15.【答案】15°;
【解析】由图可知:∠APC=∠BAP+∠PCD,即有45°+a=60°-a+30°-a,
解得:a=15°.
四、解答题
16.【解析】
解:∵AB∥CD,
∴∠ABC=∠1=65°,∠ABD+∠BDC=180°,
∵BC平分∠ABD,
∴∠ABD=2∠ABC=130°,
∴∠BDC=180°﹣∠ABD=50°,
∴∠2=∠BDC=50°.
17【解析】
解:∵a∥b∥c,
∴∠BAQ=∠1=60°,∠CAQ=∠2=36°,∠BAC=60°+36°=96°,
又AP平分∠BAC,∠BAP=×96°=48°,
∴∠PAQ=∠BAQ-∠BAP=60°-48°=12°.
18.【解析】
解: (3)不是命题,(1)、(2)、(4)是命题,题设和结论见下表.
19.【解析】
解:平行的线段:AE∥CG∥DH,AE∥BF∥DH,相等的线段:AE=BF=CG=DH.
20.【解析】
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
