2024年中考数学一轮复习讲义---反比例函数的综合应用 培优练习(含答案)
文档属性
| 名称 | 2024年中考数学一轮复习讲义---反比例函数的综合应用 培优练习(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-04-18 21:19:26 | ||
图片预览




文档简介
比例函数的综合应用 培优练习
一、课标导航
课标内容 课标要求 目标层次
反比例函数的综合应用 应用反比例函数的知识解决问题 ★★
二、核心纲要
1.反比例函数与实际问题.
2.反比例函数与一次函数的综合.
3.反比例函数与二次函数的综合.
4.反比例函数与几何的综合.
本节重点讲解:反比例函数的综合运用.
三、全能突破
基础演练
1.如图26-2-1所示,反比例函数 的图像与一次函数y=kx+b的图像交于点M、N,已知点M 的坐标为(1,3),点 N的纵坐标为-1,根据图像信息可得关于 x的方程 的解为( ).
B. -3,3 C.-1,1 D.3,-1
2.如图26-2-2所示,函数. 和函数 的图像相交于点M(2,m),N(--1,n),若. 则x的取值范围是( ).
A. x<-1或02 C.-12
3.给出下列命题及函数 和 的图像,如图26-2-3所示.
①如果 那么01;
③如果 那么-1A.正确的命题是①④ B.错误的命题是②③④
C.正确的命题是①② D.错误的命题只有③
4.阅读以下材料并填空:
问题:当x满足什么条件时,
解:设 则在同一直角坐标系中画出这两个函数的草图.如图 26-2-4(a)所示.
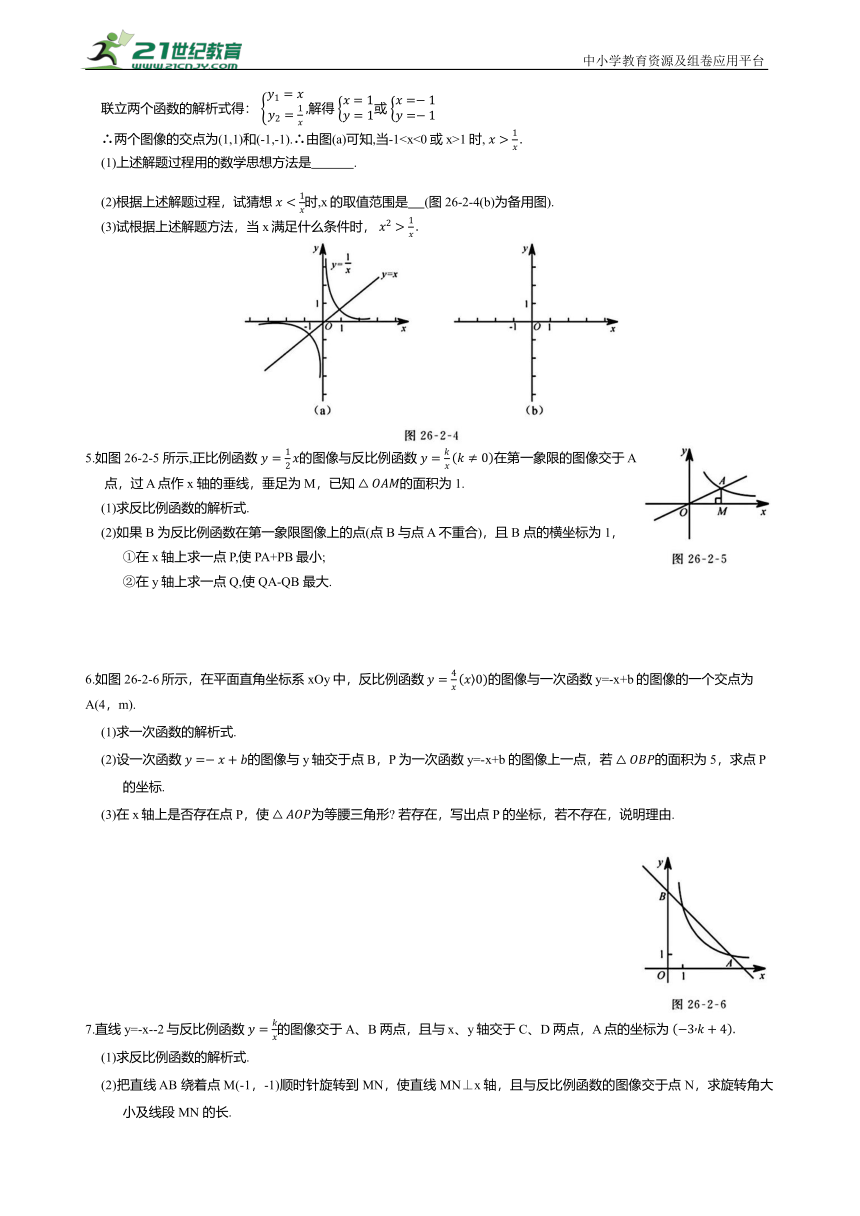
联立两个函数的解析式得: 解得 或
∴两个图像的交点为(1,1)和(-1,-1).∴由图(a)可知,当-11时,
(1)上述解题过程用的数学思想方法是 .
(2)根据上述解题过程,试猜想 时,x的取值范围是 (图26-2-4(b)为备用图).
(3)试根据上述解题方法,当x满足什么条件时,
5.如图26-2-5 所示,正比例函数 的图像与反比例函数 在第一象限的图像交于 A 点,过 A 点作x 轴的垂线,垂足为 M,已知 的面积为1.
(1)求反比例函数的解析式.
(2)如果 B 为反比例函数在第一象限图像上的点(点 B 与点 A 不重合),且 B 点的横坐标为1,
①在x轴上求一点P,使 PA+PB最小;
②在 y轴上求一点Q,使 QA-QB 最大.
6.如图 26-2-6所示,在平面直角坐标系xOy中,反比例函数 的图像与一次函数y=-x+b的图像的一个交点为A(4,m).
(1)求一次函数的解析式.
(2)设一次函数 的图像与y轴交于点B,P 为一次函数y=-x+b的图像上一点,若 的面积为5,求点 P 的坐标.
(3)在x轴上是否存在点P,使 为等腰三角形 若存在,写出点 P 的坐标,若不存在,说明理由.
7.直线y=-x--2与反比例函数 的图像交于A、B 两点,且与x、y轴交于C、D 两点,A 点的坐标为
(1)求反比例函数的解析式.
(2)把直线 AB 绕着点M(-1,-1)顺时针旋转到 MN,使直线 MN⊥x轴,且与反比例函数的图像交于点 N,求旋转角大小及线段 MN 的长.
8.据媒体报道,近期“手足口病”可能进入发病高峰期,某校根据《学校卫生工作条例》,为预防“手足口病”,对教室进行“薰药消毒”。已知药物在燃烧及释放过程中,室内空气中每立方米含药量y(毫克)与燃烧时间x(分钟)之间的关系如图26-2-7 所示(即图中线段 OA 和双曲线在A 点右侧的部分),根据图像所示信息,解答下列问题:
(1)写出从药物释放开始,y与x之间的函数关系式及自变量的取值范围.
(2)据测定,当空气中每立方米的含药量低于2毫克时,对人体无毒害作用,那么从消毒开始,至少在多长时间内,师生不能进入教室
能力提升
9.(1)若一次函数 y=kx+1的图像绕点(0,1)旋转一定角度得到的图像与反比例函数 的图像没有公共点,则实数 k的取值范围是 .
(2)如果一次函数 y=mx+n(m≠0)与反比例函数 的图像相交于点 ,那么该直线与双曲线的另一个交点为
10.如图 26-2-8 所示,A(-1,6)是双曲线 上的一点,P 为 y 轴正半轴上一点,将 A 点绕 P点逆时针旋转 90°,恰好落在双曲线上的另一点 B,则 P 点的坐标为 .
11.如图26-2-9 所示,已知一次函数和函数 的图像交于A、B 两点,过点 A 作AE⊥x轴于点E,若△AOE 的面积为2,P 是坐标平面上的点,且以点 B、O、E、P 为顶点的四边形是平行四边形,则满足条件的 P 点坐标是 .
12.在平面直角坐标系xOy中,已知反比例函数 满足:当x<0时,y随x的增大而减小.若该反比例函数的图像与直线 都经过点P,且 则实数 k= .
13.如图26-2-10 所示,过点 C(1,2)分别作 x轴、y轴的平行线,交直线 y=-x+6于 A、B 两点,若反比例函数 的图像与△ABC有公共点,则k的取值范围是 .
14.如图 26-2-11所示,M为双曲线 上的一点,过点 M 作x轴、y轴的垂线,分别交直线 y=-x+m于点 D、C两点,若直线y=--x+m与y轴交于点A,与 x轴相交于点 B,则 AD·BC 的值为 .
15.探究与应用:
已知点 P 的坐标为(m,0),在x轴上存在点Q(不与 P 点重合),以 PQ为边作正方形 PQMN,使点 M落在反比例函数 的图像上.小明对上述问题进行了探究,发现不论m取何值,符合上述条件的正方形只有两个,且一个正方形的顶点 M 在第四象限,另一个正方形的顶点 M 在第二象限.
(1)如图26-2-12所示,若反比例函数解析式为 P点坐标为(1,0),图中已画出一符合条件的一个正方形 PQMN,请你在图中画出符合条件的另一个正方形 PQ M N .
(2)请你通过改变 P 点坐标,对直线 M M的解析式y=kx+b进行探究可得k= ,若点 P 的坐标为(m,0)时,则
(3)依据(2)的规律,如果点 P 的坐标为(6,0),请你直接写出点. 和点 M 的坐标.
16.“三等分角”是数学史上一个著名问题,但仅用尺规不可能“三等分角”.下面是数学家帕普斯借助函数给出的一种“三等分锐角”的方法(如图 26-2-13 所示),将给定的锐角. 置于直角坐标系中,边 OB 在x 轴上、边 OA与函数 的图像交于点 P,以 P 为圆心,以 2OP 为半径作弧交图像于点R.分别过点 P 和 R 作 x 轴和 y 轴的平行线,两直线相交于点 M,连接 OM 得到得到 则 要明白帕普斯的方法,请你研究以下问题:
(1)设 求直线 OM 相对应的函数解析式(用含 a,b的代数式表示).
(2)分别过 P 和R 作 y 轴和x 轴的平行线,两直线相交于点 Q,请说明 Q点在直线OM 上,据此证明
17.已知反比例函数 的图像经过点.
(1)试确定此反比例函数的解析式.
(2)点O是坐标原点,将线段OA 绕O 点顺时针旋转 30°得到线段 OB,判断点 B 是否在此反比例函数的图像上,并说明理由.
(3)已知点 也在此反比例函数的图像上(其中m<0),过P点作x轴的垂线,交x轴于点 M.若线段 PM上存在一点 Q,使得△OQM的面积是 设Q点的纵坐标为n,求 的值.
18.如图26-2-14所示,抛物线 过点A(--1,0),B(3,0),其对称轴与x轴的交点为C,反比例函数 k是常数)的图像经过抛物线的顶点 D.
(1)求抛物线和反比例函数的解析式.
(2)在线段 DC上任取一点E,过点 E 作x轴平行线,交 y轴于点 F、交双曲线于点 G,连接 DF、DG、FC、GC.
①若 的面积为4,求点G的坐标;
②当 DF=GC时,求直线 DG的函数解析式.
中考链接
19.(安徽)如图 26-2-15(a)所示,在矩形 ABCD 中, ,y与x满足的反比例函数关系如图26-2-15(b)所示,等腰直角三角形 AEF 的斜边EF 过点C,M是EF 的中点,下列结论正确的是( ).
A.当 时, B.当 时,
C.当x增大时,EC·CF的值增大 D.当 y增大时,BE·DF 的值不变
20.(杭州)在平面直角坐标系内,反比例函数和二次函数 的图像交于点A(1,k)和点
(1)当 时,求反比例函数的解析式.
(2)要使反比例函数和二次函数都是 y 随着x的增大而增大,求 k应满足的条件以及x的取值范围.
中小学教育资源及组卷应用平台
(3)设二次函数的图像的顶点为 Q,当 是以AB 为斜边的直角三角形时,求 k的值.
巅峰突破
21.阅读理解:对于任意正实数a、b, 只有当a=b时,等号成立.
结论:在(a+b≥2 /ab(a、b均为正实数)中,若ab为定值p,则( 只有当a=b时,a+b有最小值
根据上述内容,回答下列问题:若 m>0,只有当 m= 时, 有最小值 .
探索应用:
(1)过原点O的直线l与反比例函数. 的图像交于P、Q两点,则线段 PQ长度的最小值为 ;若点 A 为反比例函数 在第一象限的图像上的一动点,过点 A 分别作AB⊥x轴、AC⊥y轴,垂足分别为 B、C.则四边形 OBAC 周长的最小值为 .
(2)如图26-2-16 所示,已知A(-3,0),B(0,-4),P 为双曲线. >0)上的任意一点,过点 P 作 PC⊥x轴于点C,PD⊥y轴于点 D.求四边形 ABCD 面积的最小值,并说明此时四边形 ABCD 的形状.
22.在平面直角坐标系xOy中,A,B两点在函数 的图像上,其中 轴于点C,BD⊥x轴于点 D,且 AC=1.
(1)若k =2,,则 AO的长为 ,△BOD的面积为 .
(2)如图26-2-17(a)所示,若点 B 的横坐标为k ,且k >1,当AO=AB时,求 k 的值.
(3)如图26-2-17(b)所示,OC=4,BE⊥y轴于点E,函数 的图像分别与线段 BE,BD 交于点M,N,其中( 将△OMN的面积记为S ,△BMN的面积记为S ,若. —S ,求 S与k 的函数关系式以及 S的最大值.
基础演练
1. A 2. D 3. A
4.(1)数形相结合 (2)0(3)由图像可知: 与 的交点坐标为(1.1).
∴当x>1或x<0时,
5.(1)设A 点的坐标为(a,b),则
反比例函数的解析式为
(2)由 y . A为(2.1).
又 B点横坐标为1.∴B为(1.2).
①设A点关于x轴的对称点为C,则C点的坐标为(2,-1).
令直线 BC的解析式为.y=mx+n.
∵B为( BC的解析式为y=-3x+5.
当y=0时, ∴P点为( .0).
②连接AB 并延长与y轴交于点Q,此时QA-QB 最大.
设直线 AB的解析式为y=kx+b(k≠0),则有
解得
∴直线AB的解析式为y=-x+3.
∴点Q坐标为(0,3).
6.(1)y=-x+5.
(2)由题意,得 B(0,5),∴OB=5.设 P点的横坐标为xp.
∵△OBP的面积为5.
∴点 P 的坐标为(2,3)或(-2,7).
(3)(8,0),(- /17.0),( /17.0).( .0).
7.(1)将点 A(-3,k+4)代入直线y=-x-2
得k+4=-(-3)-2解得k=-3.
∴点 A(-3.1)于是反比例函数的解析式为
(2)C、D两点的坐标为(-2,0)、(0,-2).∴在△OCD 中, 所以旋转角为 45°. 点 M、N 的坐标为(-1.-1),(-1,3)∴MN的长度为4.
8.(1)设反比例函数解析式为 将(25.6)代入解析式得,k=25×6=150,则函数解析式为
将 y=10代入解析式得 故 A(15.10).
设正比例函数解析式为y=nx.
将A(15.10)代入上式可得 则正比例函数解析式为
(2)当 得x=75.
答:从消毒开始,师生至少在75分钟内不能进入教室.
能力提升
9.(1)k<-1/4(2)(-1.-1)10. P(0.3)或P(0.4)
11. P (0.-4). P (-2.-4). P (2.4) 12.
13.2≤k≤9
14.2
15.(1)如下图所示
(2)k=-1. b=m
(3)M 的坐标为( ,M的坐标为(3+
16.(1)设直线OM的函数关系式为y=kx,P(a, )、R(b, 则M(
∴直线OM的函数关系式为
(2)∵Q的坐标 满足
∴点Q在直线OM 上.
∵四边形 PQRM是矩形。
∴∠SQR=∠SRQ.
∵PR=2OP,∴PS=OP= PR.
∴∠POS=∠PSO.
∵∠PSQ是△SQR的一个外角。
∴∠PSQ=2∠SQR.
∴∠POS=2∠SQR.
∵QR∥OB.
∴∠MOB=∠SQR.
∴∠POS=2∠MOB.
(2)如下图所示,过点A作x轴的垂线交x轴于点C.
在 Rt△AOC 中, OC= , AC = 1.可得 OA =
由题意,∠AOB=30°,OB=OA=2,∴∠BOC=60°.
过点 B作x轴的垂线交x轴于点 D.
在 Rt△BOD 中,可得 BD= . OD=1.
∴B点坐标为(-1, ).
将x=-1代入 中,得
∴点B(-1. )在反比例函数 的图像上.
(3)由 得
∵点 在反比例函数 的图像上,其中
∵PQ⊥x轴,∴Q点的坐标为(m,n).
∵△OQM的面积是
18.(1)∵抛物线 过点A(-1,0),B(3,0)
解得
∴抛物线的解析式为. ∴顶点 D(1.4)函数 m是常数)图像经过 D(1,4),
∴k=4.
(2)①设G点的坐标为
据题意,可得 E 点 的 坐 标 为(1.4/m). F.点 的坐标为((0.4m).
∵m>1,∴FG=m,DE=4- /m.
由△DFG的面积为4,即 得m=3.
∴点G的坐标为
②∵FC∥DG,∴当FD=CG时,有两种情况:
当 FD∥CG时,四边形 DFCG是平行四边形.
由上题得 得m=2.
∴点G的坐标是(2.2).
设直线 DG的函数解析式为y=kx+b,把点 D,G的坐标代入。
得 解得
∴直线AB的函数解析式是y=-2x+6.
当 FD与CG 所在直线不平行时,四边形 ADCB 是等腰梯形.
则 DC=FG,∴m=4,∴点G的坐标是(4,1).
设直线AB的函数解析式为y=kx+b.把点 D,G 的坐标代入。
得 解得
∴直线AB的函数解析式是y=-x+5.
综上所述,所求直线 DG的函数解析式是y=-2x+6或y=-x+5.
中考链接
19. D
20.(1)当k=-2时,A(1,-2).∵A在反比例函数图像上。
∴设反比例函数的解析式为: 代入A(1,-2)得: 解得:m=-2.
∴反比例函数的解析式为
(2)∵要使反比例函数和二次函数都是 y随着x的增大而增大,∴k<0.
∵二次函数 的对称轴为:直线
要使二次函数. 满足上述条件,在 k<0的情况下,x必须在对称轴的左边。
即 时,才能使得y随着x的增大而增大,∴综上所述。,k<0」且
(3)由(2)可得
∵△ABQ是以AB 为斜边的直角三角形,A 点与B 点关于原点对称(下图是其中的一种情况)
∴原点O平分AB,∴OQ=OA=OB,
作 AD⊥OC,QC⊥OC.
解得
21.阅读理解:1:2
探索应用:(1)2/2;4
(2)设P(x, ),则C(x,0), D(0. ).
化简得
只有当x= ,即x=3|时,等号成立.
∴S≥2×6+12=24.∴S四边形ABCD有最小值24.
此时,P(3,4),C(3,0),D(0,4),AB=BC=CD=DA=5.
∴四边形ABCD 是菱形.
22.(1) AO的长为 ,△BOD 的面积为1;
(2)∵A,B 两点在函数 的图像上,
∴点A,B的坐标分别为(1,k ),(k ,1).
∵AO=AB,由勾股定理得
解得 或
(3) 如下图所示,∵OC=4,∴点A的坐标为(1,4).
设点 B的坐标为
∵BE⊥y轴于点E,BD⊥x轴于点 D,
∴四边形 ODBE 为矩形,且 S四边形ODBE=4,点 M 的纵坐标为 ,点N的横坐标为m.
∵点M,N在函数 的图像上,
∴点M的坐标为 点 N 的坐标为
·
其中 而
∴当k =2时,S的最大值为1.
一、课标导航
课标内容 课标要求 目标层次
反比例函数的综合应用 应用反比例函数的知识解决问题 ★★
二、核心纲要
1.反比例函数与实际问题.
2.反比例函数与一次函数的综合.
3.反比例函数与二次函数的综合.
4.反比例函数与几何的综合.
本节重点讲解:反比例函数的综合运用.
三、全能突破
基础演练
1.如图26-2-1所示,反比例函数 的图像与一次函数y=kx+b的图像交于点M、N,已知点M 的坐标为(1,3),点 N的纵坐标为-1,根据图像信息可得关于 x的方程 的解为( ).
B. -3,3 C.-1,1 D.3,-1
2.如图26-2-2所示,函数. 和函数 的图像相交于点M(2,m),N(--1,n),若. 则x的取值范围是( ).
A. x<-1或0
3.给出下列命题及函数 和 的图像,如图26-2-3所示.
①如果 那么0
③如果 那么-1
C.正确的命题是①② D.错误的命题只有③
4.阅读以下材料并填空:
问题:当x满足什么条件时,
解:设 则在同一直角坐标系中画出这两个函数的草图.如图 26-2-4(a)所示.
联立两个函数的解析式得: 解得 或
∴两个图像的交点为(1,1)和(-1,-1).∴由图(a)可知,当-1
(1)上述解题过程用的数学思想方法是 .
(2)根据上述解题过程,试猜想 时,x的取值范围是 (图26-2-4(b)为备用图).
(3)试根据上述解题方法,当x满足什么条件时,
5.如图26-2-5 所示,正比例函数 的图像与反比例函数 在第一象限的图像交于 A 点,过 A 点作x 轴的垂线,垂足为 M,已知 的面积为1.
(1)求反比例函数的解析式.
(2)如果 B 为反比例函数在第一象限图像上的点(点 B 与点 A 不重合),且 B 点的横坐标为1,
①在x轴上求一点P,使 PA+PB最小;
②在 y轴上求一点Q,使 QA-QB 最大.
6.如图 26-2-6所示,在平面直角坐标系xOy中,反比例函数 的图像与一次函数y=-x+b的图像的一个交点为A(4,m).
(1)求一次函数的解析式.
(2)设一次函数 的图像与y轴交于点B,P 为一次函数y=-x+b的图像上一点,若 的面积为5,求点 P 的坐标.
(3)在x轴上是否存在点P,使 为等腰三角形 若存在,写出点 P 的坐标,若不存在,说明理由.
7.直线y=-x--2与反比例函数 的图像交于A、B 两点,且与x、y轴交于C、D 两点,A 点的坐标为
(1)求反比例函数的解析式.
(2)把直线 AB 绕着点M(-1,-1)顺时针旋转到 MN,使直线 MN⊥x轴,且与反比例函数的图像交于点 N,求旋转角大小及线段 MN 的长.
8.据媒体报道,近期“手足口病”可能进入发病高峰期,某校根据《学校卫生工作条例》,为预防“手足口病”,对教室进行“薰药消毒”。已知药物在燃烧及释放过程中,室内空气中每立方米含药量y(毫克)与燃烧时间x(分钟)之间的关系如图26-2-7 所示(即图中线段 OA 和双曲线在A 点右侧的部分),根据图像所示信息,解答下列问题:
(1)写出从药物释放开始,y与x之间的函数关系式及自变量的取值范围.
(2)据测定,当空气中每立方米的含药量低于2毫克时,对人体无毒害作用,那么从消毒开始,至少在多长时间内,师生不能进入教室
能力提升
9.(1)若一次函数 y=kx+1的图像绕点(0,1)旋转一定角度得到的图像与反比例函数 的图像没有公共点,则实数 k的取值范围是 .
(2)如果一次函数 y=mx+n(m≠0)与反比例函数 的图像相交于点 ,那么该直线与双曲线的另一个交点为
10.如图 26-2-8 所示,A(-1,6)是双曲线 上的一点,P 为 y 轴正半轴上一点,将 A 点绕 P点逆时针旋转 90°,恰好落在双曲线上的另一点 B,则 P 点的坐标为 .
11.如图26-2-9 所示,已知一次函数和函数 的图像交于A、B 两点,过点 A 作AE⊥x轴于点E,若△AOE 的面积为2,P 是坐标平面上的点,且以点 B、O、E、P 为顶点的四边形是平行四边形,则满足条件的 P 点坐标是 .
12.在平面直角坐标系xOy中,已知反比例函数 满足:当x<0时,y随x的增大而减小.若该反比例函数的图像与直线 都经过点P,且 则实数 k= .
13.如图26-2-10 所示,过点 C(1,2)分别作 x轴、y轴的平行线,交直线 y=-x+6于 A、B 两点,若反比例函数 的图像与△ABC有公共点,则k的取值范围是 .
14.如图 26-2-11所示,M为双曲线 上的一点,过点 M 作x轴、y轴的垂线,分别交直线 y=-x+m于点 D、C两点,若直线y=--x+m与y轴交于点A,与 x轴相交于点 B,则 AD·BC 的值为 .
15.探究与应用:
已知点 P 的坐标为(m,0),在x轴上存在点Q(不与 P 点重合),以 PQ为边作正方形 PQMN,使点 M落在反比例函数 的图像上.小明对上述问题进行了探究,发现不论m取何值,符合上述条件的正方形只有两个,且一个正方形的顶点 M 在第四象限,另一个正方形的顶点 M 在第二象限.
(1)如图26-2-12所示,若反比例函数解析式为 P点坐标为(1,0),图中已画出一符合条件的一个正方形 PQMN,请你在图中画出符合条件的另一个正方形 PQ M N .
(2)请你通过改变 P 点坐标,对直线 M M的解析式y=kx+b进行探究可得k= ,若点 P 的坐标为(m,0)时,则
(3)依据(2)的规律,如果点 P 的坐标为(6,0),请你直接写出点. 和点 M 的坐标.
16.“三等分角”是数学史上一个著名问题,但仅用尺规不可能“三等分角”.下面是数学家帕普斯借助函数给出的一种“三等分锐角”的方法(如图 26-2-13 所示),将给定的锐角. 置于直角坐标系中,边 OB 在x 轴上、边 OA与函数 的图像交于点 P,以 P 为圆心,以 2OP 为半径作弧交图像于点R.分别过点 P 和 R 作 x 轴和 y 轴的平行线,两直线相交于点 M,连接 OM 得到得到 则 要明白帕普斯的方法,请你研究以下问题:
(1)设 求直线 OM 相对应的函数解析式(用含 a,b的代数式表示).
(2)分别过 P 和R 作 y 轴和x 轴的平行线,两直线相交于点 Q,请说明 Q点在直线OM 上,据此证明
17.已知反比例函数 的图像经过点.
(1)试确定此反比例函数的解析式.
(2)点O是坐标原点,将线段OA 绕O 点顺时针旋转 30°得到线段 OB,判断点 B 是否在此反比例函数的图像上,并说明理由.
(3)已知点 也在此反比例函数的图像上(其中m<0),过P点作x轴的垂线,交x轴于点 M.若线段 PM上存在一点 Q,使得△OQM的面积是 设Q点的纵坐标为n,求 的值.
18.如图26-2-14所示,抛物线 过点A(--1,0),B(3,0),其对称轴与x轴的交点为C,反比例函数 k是常数)的图像经过抛物线的顶点 D.
(1)求抛物线和反比例函数的解析式.
(2)在线段 DC上任取一点E,过点 E 作x轴平行线,交 y轴于点 F、交双曲线于点 G,连接 DF、DG、FC、GC.
①若 的面积为4,求点G的坐标;
②当 DF=GC时,求直线 DG的函数解析式.
中考链接
19.(安徽)如图 26-2-15(a)所示,在矩形 ABCD 中, ,y与x满足的反比例函数关系如图26-2-15(b)所示,等腰直角三角形 AEF 的斜边EF 过点C,M是EF 的中点,下列结论正确的是( ).
A.当 时, B.当 时,
C.当x增大时,EC·CF的值增大 D.当 y增大时,BE·DF 的值不变
20.(杭州)在平面直角坐标系内,反比例函数和二次函数 的图像交于点A(1,k)和点
(1)当 时,求反比例函数的解析式.
(2)要使反比例函数和二次函数都是 y 随着x的增大而增大,求 k应满足的条件以及x的取值范围.
中小学教育资源及组卷应用平台
(3)设二次函数的图像的顶点为 Q,当 是以AB 为斜边的直角三角形时,求 k的值.
巅峰突破
21.阅读理解:对于任意正实数a、b, 只有当a=b时,等号成立.
结论:在(a+b≥2 /ab(a、b均为正实数)中,若ab为定值p,则( 只有当a=b时,a+b有最小值
根据上述内容,回答下列问题:若 m>0,只有当 m= 时, 有最小值 .
探索应用:
(1)过原点O的直线l与反比例函数. 的图像交于P、Q两点,则线段 PQ长度的最小值为 ;若点 A 为反比例函数 在第一象限的图像上的一动点,过点 A 分别作AB⊥x轴、AC⊥y轴,垂足分别为 B、C.则四边形 OBAC 周长的最小值为 .
(2)如图26-2-16 所示,已知A(-3,0),B(0,-4),P 为双曲线. >0)上的任意一点,过点 P 作 PC⊥x轴于点C,PD⊥y轴于点 D.求四边形 ABCD 面积的最小值,并说明此时四边形 ABCD 的形状.
22.在平面直角坐标系xOy中,A,B两点在函数 的图像上,其中 轴于点C,BD⊥x轴于点 D,且 AC=1.
(1)若k =2,,则 AO的长为 ,△BOD的面积为 .
(2)如图26-2-17(a)所示,若点 B 的横坐标为k ,且k >1,当AO=AB时,求 k 的值.
(3)如图26-2-17(b)所示,OC=4,BE⊥y轴于点E,函数 的图像分别与线段 BE,BD 交于点M,N,其中( 将△OMN的面积记为S ,△BMN的面积记为S ,若. —S ,求 S与k 的函数关系式以及 S的最大值.
基础演练
1. A 2. D 3. A
4.(1)数形相结合 (2)0
∴当x>1或x<0时,
5.(1)设A 点的坐标为(a,b),则
反比例函数的解析式为
(2)由 y . A为(2.1).
又 B点横坐标为1.∴B为(1.2).
①设A点关于x轴的对称点为C,则C点的坐标为(2,-1).
令直线 BC的解析式为.y=mx+n.
∵B为( BC的解析式为y=-3x+5.
当y=0时, ∴P点为( .0).
②连接AB 并延长与y轴交于点Q,此时QA-QB 最大.
设直线 AB的解析式为y=kx+b(k≠0),则有
解得
∴直线AB的解析式为y=-x+3.
∴点Q坐标为(0,3).
6.(1)y=-x+5.
(2)由题意,得 B(0,5),∴OB=5.设 P点的横坐标为xp.
∵△OBP的面积为5.
∴点 P 的坐标为(2,3)或(-2,7).
(3)(8,0),(- /17.0),( /17.0).( .0).
7.(1)将点 A(-3,k+4)代入直线y=-x-2
得k+4=-(-3)-2解得k=-3.
∴点 A(-3.1)于是反比例函数的解析式为
(2)C、D两点的坐标为(-2,0)、(0,-2).∴在△OCD 中, 所以旋转角为 45°. 点 M、N 的坐标为(-1.-1),(-1,3)∴MN的长度为4.
8.(1)设反比例函数解析式为 将(25.6)代入解析式得,k=25×6=150,则函数解析式为
将 y=10代入解析式得 故 A(15.10).
设正比例函数解析式为y=nx.
将A(15.10)代入上式可得 则正比例函数解析式为
(2)当 得x=75.
答:从消毒开始,师生至少在75分钟内不能进入教室.
能力提升
9.(1)k<-1/4(2)(-1.-1)10. P(0.3)或P(0.4)
11. P (0.-4). P (-2.-4). P (2.4) 12.
13.2≤k≤9
14.2
15.(1)如下图所示
(2)k=-1. b=m
(3)M 的坐标为( ,M的坐标为(3+
16.(1)设直线OM的函数关系式为y=kx,P(a, )、R(b, 则M(
∴直线OM的函数关系式为
(2)∵Q的坐标 满足
∴点Q在直线OM 上.
∵四边形 PQRM是矩形。
∴∠SQR=∠SRQ.
∵PR=2OP,∴PS=OP= PR.
∴∠POS=∠PSO.
∵∠PSQ是△SQR的一个外角。
∴∠PSQ=2∠SQR.
∴∠POS=2∠SQR.
∵QR∥OB.
∴∠MOB=∠SQR.
∴∠POS=2∠MOB.
(2)如下图所示,过点A作x轴的垂线交x轴于点C.
在 Rt△AOC 中, OC= , AC = 1.可得 OA =
由题意,∠AOB=30°,OB=OA=2,∴∠BOC=60°.
过点 B作x轴的垂线交x轴于点 D.
在 Rt△BOD 中,可得 BD= . OD=1.
∴B点坐标为(-1, ).
将x=-1代入 中,得
∴点B(-1. )在反比例函数 的图像上.
(3)由 得
∵点 在反比例函数 的图像上,其中
∵PQ⊥x轴,∴Q点的坐标为(m,n).
∵△OQM的面积是
18.(1)∵抛物线 过点A(-1,0),B(3,0)
解得
∴抛物线的解析式为. ∴顶点 D(1.4)函数 m是常数)图像经过 D(1,4),
∴k=4.
(2)①设G点的坐标为
据题意,可得 E 点 的 坐 标 为(1.4/m). F.点 的坐标为((0.4m).
∵m>1,∴FG=m,DE=4- /m.
由△DFG的面积为4,即 得m=3.
∴点G的坐标为
②∵FC∥DG,∴当FD=CG时,有两种情况:
当 FD∥CG时,四边形 DFCG是平行四边形.
由上题得 得m=2.
∴点G的坐标是(2.2).
设直线 DG的函数解析式为y=kx+b,把点 D,G的坐标代入。
得 解得
∴直线AB的函数解析式是y=-2x+6.
当 FD与CG 所在直线不平行时,四边形 ADCB 是等腰梯形.
则 DC=FG,∴m=4,∴点G的坐标是(4,1).
设直线AB的函数解析式为y=kx+b.把点 D,G 的坐标代入。
得 解得
∴直线AB的函数解析式是y=-x+5.
综上所述,所求直线 DG的函数解析式是y=-2x+6或y=-x+5.
中考链接
19. D
20.(1)当k=-2时,A(1,-2).∵A在反比例函数图像上。
∴设反比例函数的解析式为: 代入A(1,-2)得: 解得:m=-2.
∴反比例函数的解析式为
(2)∵要使反比例函数和二次函数都是 y随着x的增大而增大,∴k<0.
∵二次函数 的对称轴为:直线
要使二次函数. 满足上述条件,在 k<0的情况下,x必须在对称轴的左边。
即 时,才能使得y随着x的增大而增大,∴综上所述。,k<0」且
(3)由(2)可得
∵△ABQ是以AB 为斜边的直角三角形,A 点与B 点关于原点对称(下图是其中的一种情况)
∴原点O平分AB,∴OQ=OA=OB,
作 AD⊥OC,QC⊥OC.
解得
21.阅读理解:1:2
探索应用:(1)2/2;4
(2)设P(x, ),则C(x,0), D(0. ).
化简得
只有当x= ,即x=3|时,等号成立.
∴S≥2×6+12=24.∴S四边形ABCD有最小值24.
此时,P(3,4),C(3,0),D(0,4),AB=BC=CD=DA=5.
∴四边形ABCD 是菱形.
22.(1) AO的长为 ,△BOD 的面积为1;
(2)∵A,B 两点在函数 的图像上,
∴点A,B的坐标分别为(1,k ),(k ,1).
∵AO=AB,由勾股定理得
解得 或
(3) 如下图所示,∵OC=4,∴点A的坐标为(1,4).
设点 B的坐标为
∵BE⊥y轴于点E,BD⊥x轴于点 D,
∴四边形 ODBE 为矩形,且 S四边形ODBE=4,点 M 的纵坐标为 ,点N的横坐标为m.
∵点M,N在函数 的图像上,
∴点M的坐标为 点 N 的坐标为
·
其中 而
∴当k =2时,S的最大值为1.
同课章节目录
