2024年中考数学一轮复习讲义---相似三角形的综合应用(含答案)
文档属性
| 名称 | 2024年中考数学一轮复习讲义---相似三角形的综合应用(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-04-18 21:18:54 | ||
图片预览


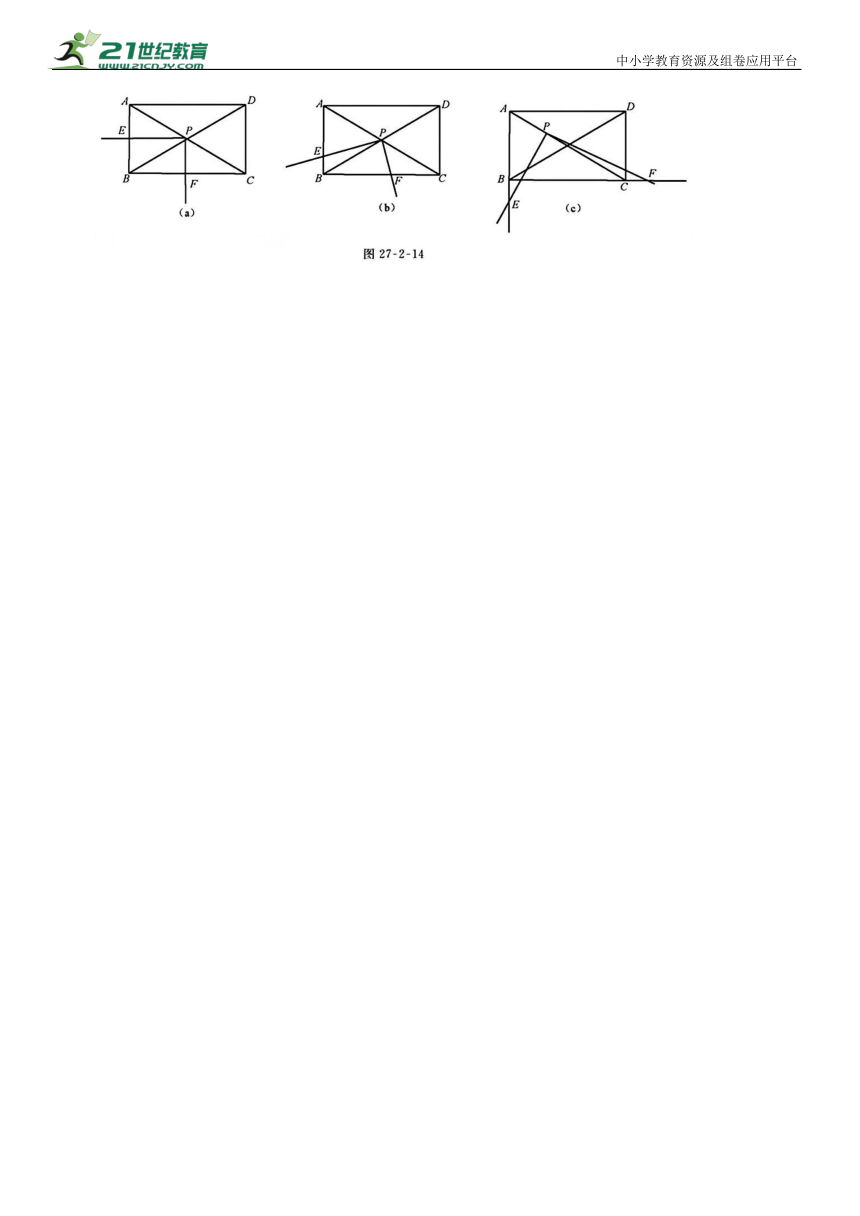
文档简介
相似三角形的综合应用
一、课标导航
课标内容 课标要求 目标层次
相似三角形的综合应用 利用相似三角形的知识解决问题 ★★
二、核心纲要
常见的相似模型如下:
(1)母子型 (2)双垂型 (3)三垂直型
本节重点讲解:模型的应用,相似三角形与其他知识的综合.
三、全能突破
基础演练
1.如图27-2-1 所示,正方形 ABCD 的边长为4,M、N 分别是 BC、CD 上的两个动点,且始终保持 当 时,四边形 ABCN的面积最大.
2.如图27-2-2所示,在等边 中,P 为BC 上一点,D为AC 上一点,且 则△AB 的周长为 .
3.如图27-2-3 所示,在△ABC中,AB=AC= 5,BC= 8,D,E 分别为BC、AB边上一点,
(1)求证:△BDE∽△CAD.
(2)若CD=2,求 BE的长.
(3)设CD=x,AE=y,求 y关于x 的函数关系式,并写出自变量 x的取值范围.
4.如图27-2-4 所示,C 是以AB 为直径的⊙O上一点,过点 O 作OE⊥AC 于点 E,过点 A 作⊙O的切线交OE 的延长线于点F,连接CF 并延长交 BA 的延长线于点 P.
(1)求证:PC是⊙O的切线.
(2)若 AB=4,AP: PC=1:2,求CF的长.
5.如图27-2-5 所示,AB 为⊙O 的直径,BC 切⊙O 于点 B,AC 交⊙O 于点 D,E 为 BC中点.
求证:(1)DE为⊙O的切线.
(2)延长 ED 交 BA 的延长线于 F,若DF=4,AF=2,求 BC的长.
能力提升
6.如图27-2-6所示,已知AB∥EF∥CD,AB=30,CD=50,则 EF的长为 .
7.如图27-2-7所示,在Rt△ABC中,∠ABC 是直角,. ,P 是BC 边上的动点,设.BP=x,若能在 AC 边上找到一点Q,使 则x的取值范围是 .
8.如图27-2-8 所示,正方形 ABCD的边长为10,内部有6个全等的正方形,小正方形的顶点 E、F、G、H分别落在边AD、AB、BC、CD上,则 DE 的长为 .
9.操作:如图 27-2-9 所示,在正方形 ABCD中,P 是CD上一动点(与C、D 不重合),使三角板的直角顶点与点 P 重合,并且一条直角边始终经过点 B,另一直角边与正方形的某一边所在直线交于点 E.
探究:①观察操作结果,哪一个三角形与△BPC 相似,写出你的结论(找出两对即可);并选择其中一组说明理由.
②当点 P 位于CD 的中点时,直接写出①中找到的两对相似三角形的相似比和面积比.
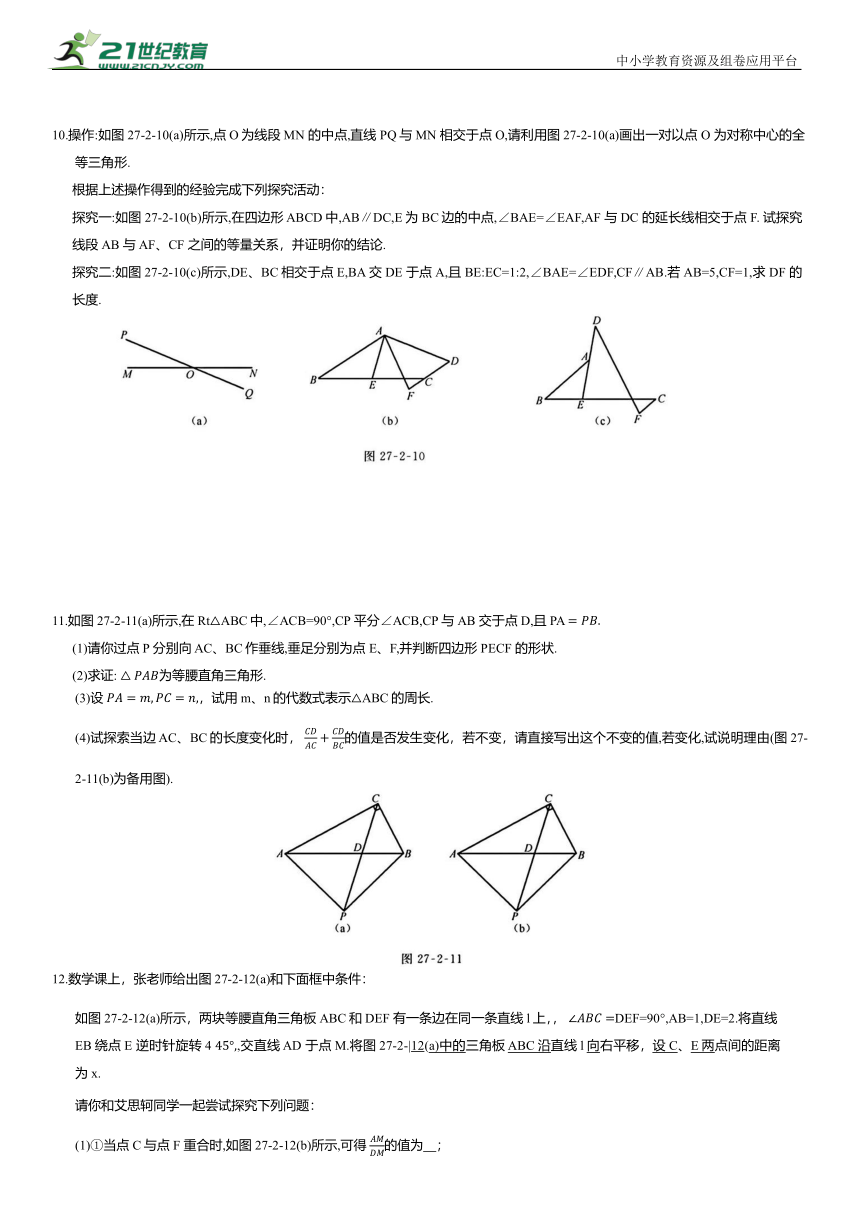
10.操作:如图 27-2-10(a)所示,点O为线段MN 的中点,直线 PQ与MN 相交于点O,请利用图27-2-10(a)画出一对以点 O 为对称中心的全等三角形.
根据上述操作得到的经验完成下列探究活动:
探究一:如图 27-2-10(b)所示,在四边形 ABCD中,AB∥DC,E为BC边的中点,∠BAE=∠EAF,AF 与DC 的延长线相交于点 F. 试探究线段AB 与AF、CF 之间的等量关系,并证明你的结论.
探究二:如图27-2-10(c)所示,DE、BC相交于点E,BA交DE 于点A,且 BE:EC=1:2,∠BAE=∠EDF,CF∥AB.若AB=5,CF=1,求 DF 的长度.
11.如图27-2-11(a)所示,在 Rt△ABC中,∠ACB=90°,CP 平分∠ACB,CP 与AB 交于点D,且 PA
(1)请你过点 P 分别向 AC、BC作垂线,垂足分别为点 E、F,并判断四边形 PECF 的形状.
(2)求证: 为等腰直角三角形.
(3)设 ,试用m、n的代数式表示△ABC的周长.
(4)试探索当边 AC、BC的长度变化时, 的值是否发生变化,若不变,请直接写出这个不变的值,若变化,试说明理由(图27-2-11(b)为备用图).
12.数学课上,张老师给出图27-2-12(a)和下面框中条件:
如图27-2-12(a)所示,两块等腰直角三角板ABC和DEF 有一条边在同一条直线l上,, DEF=90°,AB=1,DE=2.将直线 EB绕点 E 逆时针旋转4 ,交直线 AD 于点M.将图27-2-|12(a)中的三角板 ABC沿直线l向右平移,设C、E两点间的距离为x.
请你和艾思轲同学一起尝试探究下列问题:
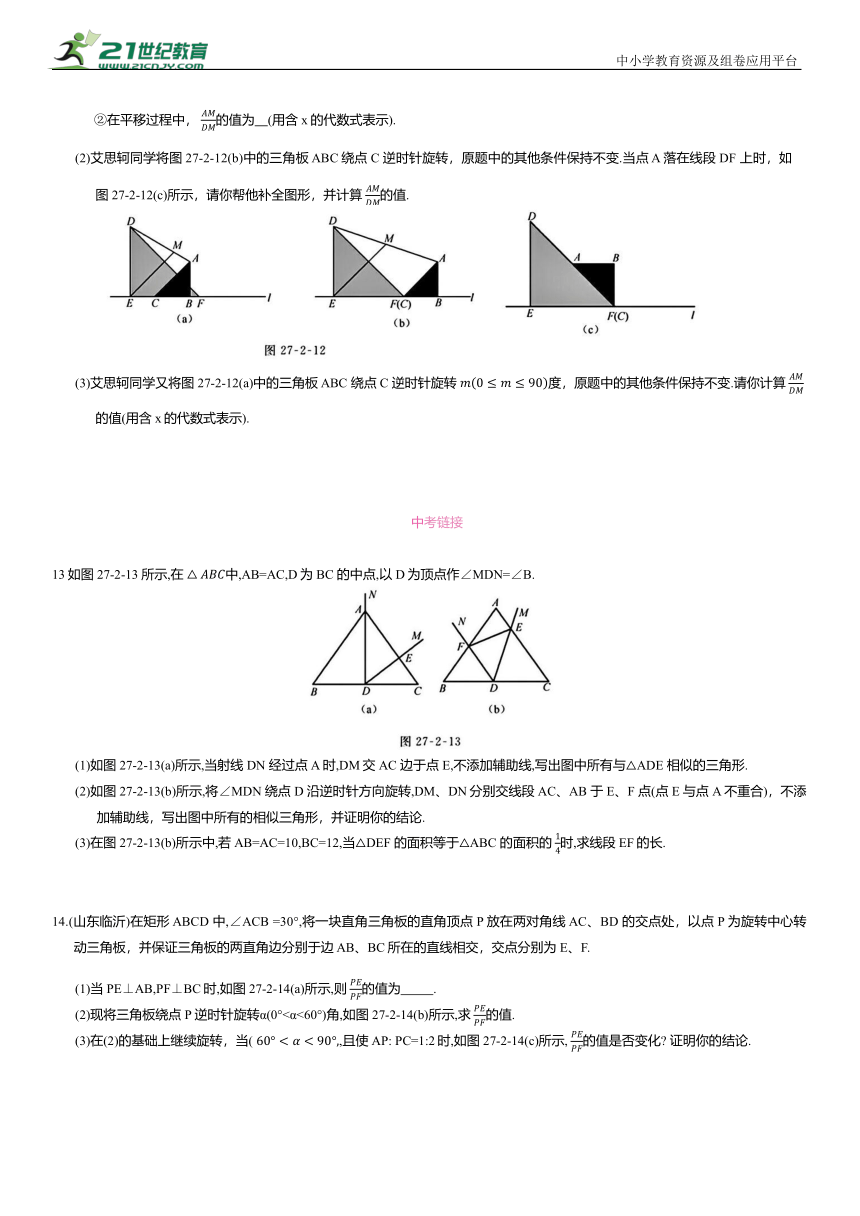
(1)①当点C与点 F 重合时,如图27-2-12(b)所示,可得 的值为 ;
②在平移过程中, 的值为 (用含 x的代数式表示).
(2)艾思轲同学将图27-2-12(b)中的三角板 ABC绕点C 逆时针旋转,原题中的其他条件保持不变.当点 A 落在线段 DF 上时,如图 27-2-12(c)所示,请你帮他补全图形,并计算 的值.
(3)艾思轲同学又将图27-2-12(a)中的三角板 ABC 绕点C 逆时针旋转 度,原题中的其他条件保持不变.请你计算 的值(用含x的代数式表示).
中考链接
13如图 27-2-13 所示,在 中,AB=AC,D为BC 的中点,以 D为顶点作∠MDN=∠B.
(1)如图27-2-13(a)所示,当射线 DN 经过点A 时,DM交AC 边于点 E,不添加辅助线,写出图中所有与△ADE 相似的三角形.
(2)如图27-2-13(b)所示,将∠MDN 绕点D 沿逆时针方向旋转,DM、DN分别交线段AC、AB 于 E、F 点(点 E 与点A 不重合),不添加辅助线,写出图中所有的相似三角形,并证明你的结论.
(3)在图27-2-13(b)所示中,若AB=AC=10,BC=12,当△DEF 的面积等于△ABC 的面积的 时,求线段EF的长.
14.(山东临沂)在矩形 ABCD 中,∠ACB =30°,将一块直角三角板的直角顶点 P 放在两对角线AC、BD 的交点处,以点 P 为旋转中心转动三角板,并保证三角板的两直角边分别于边 AB、BC所在的直线相交,交点分别为 E、F.
(1)当 PE⊥AB,PF⊥BC时,如图27-2-14(a)所示,则 的值为 .
(2)现将三角板绕点 P 逆时针旋转α(0°<α<60°)角,如图 27-2-14(b)所示,求 的值.
(3)在(2)的基础上继续旋转,当( ,且使AP: PC=1:2时,如图27-2-14(c)所示, 的值是否变化 证明你的结论.
中小学教育资源及组卷应用平台
巅峰突破
15.在平面内,先将一个多边形以点O为位似中心放大或缩小,使所得多边形与原多边形对应线段的比为 k,并且原多边形上的任一点 P,它的对应点 在线段OP 或其延长线上;接着将所得多边形以点O为旋转中心,逆时针旋转一个角度θ,这种经过缩放和旋转的图形变换叫做旋转相似变换,记为O(k,θ),其中点O叫做旋转相似中心,k叫做相似比,θ叫做旋转角.
(1)填空
①如图 27-2-15(a)所示,将 以点A 为旋转相似中心放大为原来的 2 倍,再逆时针旋转60°,得到 ,这个旋转相似变换记为 A( , );
②如图27-2-15(b)所示,. 是边长为 1cm的等边三角形,将它作旋转相似变换 90),得到 ,则线段 BD的长为 cm.
(2)如图27-2-15(c)所示,分别以锐角三角形 ABC 的三边 AB、BC、CA 为边向外作正方形 ADEB、BF-GC、CHIA,点 分别是这三个正方形的对角线交点,试分别利用, 与 与 之间的关系,运用旋转相似变换的知识说明线段( 与 之间的关系.
16.(1)如图27-2-16(a)所示,在四边形 ABDC中,. 猜想 与 的11大小关系(直接写出结论)
(2)如图27-2-16(b)所示,在四边形 ABDC 中,. 猜想 2AD 与 的大小关系并证明.
基础演练
1.2 2.9
3.(1)∵AB=AC,∴∠B=∠C.∵ ∠ADE+∠BDE=∠ADB =∠C+∠CAD,∠ADE=∠C,
∴∠BDE =∠CAD. ∴△BDE∽△CAD.
(2)由(1)得DB=△D.∵AB=AC= 5,BC= 8,CD=2,
∴DB=BC-CD=6.
(3)由已知BE=5-y;BD=8-x.∵△BDE∽△CAD.
即
4.(1)连接OC,如下图所示 .∵ OE⊥AC,∴AE=CE.
∴FA=FC.
∴∠FAC=∠FCA.∵OA=OC,∴∠OAC=∠OCA.
∴ ∠OAC+∠FAC=∠OCA+∠FCA. 即∠FAO=∠FCO.
∵FA与⊙O相切,且AB是⊙O的直径,∴ FA⊥AB.
∴∠FCO=∠FAO=90°.∴ PC 是⊙O的切线.
(2)∵∠PCO=90°,即∠ACO +∠ACP =90°.
又∵∠BCO+∠ACO=90°,∴∠ACP=∠BCO.
∵BO=CO.∴∠BCO=∠B.∴∠ACP=∠B.
∵∠P公共角,∴△PCA∽△PBC.
∵FA与⊙O相切,∴∠FAO=90°.∴ OF∥BC.
∴∠AOF=∠ABC.∴△ABC∽△FOA.
∴AF=1.∴CF=1.
5.(1)如下图所示,连接OD、BD.
∵在⊙O 中,OD=OB,∴∠1=∠2.
∵AB是⊙O的直径,∴∠ADB=∠CDB=90°.
∵E为BC中点,
∴∠3=∠4.∵BC切⊙O于点B,∴∠EBA=90°.
∴∠1+∠3=∠2+∠4=90°,
即∠ODE=90°.∴OD⊥DE.∵点 D 在⊙O上,∴DE是⊙O的切线.
(2)∵OD⊥DE,∴∠FDO=90°.
设( ,
解得r=3.
∴OA=OD=3,FB=8.
∵∠F=∠F,∠FDO=∠FBE=90°.
∵E为BC中点,∴BC=2BE=12.
能力提升
6. 7.3≤x≤4 8.2
9.分两种情况:
①如图(a)所示,
∵∠BPE=90°.
∴∠BPC+∠DPE=90°,
又∠BPC+∠PBC=90°,
∴∠PBC=∠DPE,
又∠C=∠D=90°.
∴△BPC∽△PED.
如图(b)所示,同理可证△BPC∽△BEP∽△PEC.
②如图(a)所示,
∵△BPC∽△PED,
∴△PED与△BPC 的周长比等于对应边的比,即 PD与BC 的比,
∵点P位于CD 的中点,
∴PD与BC 的比为1:2,
∴△PED与△BPC的周长比1:2,面积比1:4.
如图(b)所示,
∵△BPC∽△BEP,∴△BEP与△BPC 的周长比等于对应边的比,即 BP与BC的比.
∵点 P位于CD的中点,设 BC=2k,则 PC=k,BP=/5k,
∴BP与BC的比为 :2,
△BEP与△BPC的周长比为 :2.
△BEP与△BPC的面积比为5:4.
同理:△PCE∽△BPC,周长比1:2,面积比1:4.
10.图略;
探究一:
结论:AB=AF+CF.
证明:分别延长AE、DF 交于点M,∵E为BC 的中点,
∴BE=CE.∵AB∥CD.∴∠BAE=∠M.
∵∠AEB=∠MEC,∴△ABE≌△MCE.∴AB=MC.
又∵∠BAE=∠EAF,∴∠M=∠EAF.∴MF=AF.
又∵MC=MF+CF,∴AB=AF+CF.
探究二:
分别延长 DE、CF交于点G,
∵AB∥CF,∴∠B=∠C,∠BAE=∠G.
∴△ABE∽△GCE∴△C=BC.
∵FC=1,∴GF=9.
又∵∠BAE=∠EDF.∴∠G=∠EDF.∴GF=DF.
∴DF=9.
11.(1)过点 P分别作 PE⊥AC、PF⊥CB,垂足分别为E、F,∵∠ACB=90°,PE⊥AC,PF⊥CB,∴四边形 PECF 是矩形.
又∵点 P 在∠ACB 的角平分线上,且 PE⊥AC、PF⊥CB,∴PE=PF.
∴四边形 PECF 是正方形.
(2)在 Rt△AEP和Rt△BFP中,
∵PE=PF,PA=PB,
∴Rt△AEP≌Rt△BFP.∴∠APE=∠BPF.
∵∠EPF= 90°,∴∠APB= 90°.∵PA=PB.
∴△PAB是等腰直角三角形.
(3)如下图所示,在 Rt△PAB中,∠APB=90°,PA=PB,
由(2)可知,Rt△AEP≌Rt△BFP,可得 AE=BF,CE=CF,
∴CA+CB=CE+EA+CB=CE+CF=2CE.
又
的周长为:AB+BC+
(4)不变
如下图所示.∵∠1=∠2=∠3=∠4=45°,且∠ADC=∠PDB.
∴△ADC∽△PDB.∴≌D=△FB.(即
同理可得,△CDB∽△ADP,得到
又 PA= PB,则①+②得:
12.(1)①1.② .
(2)连接AE,补全图形如下图所示.
∵△ABC 和△DEF 是等腰直角三角形,AB = 1. DE
= 2.
∴BC= 1,EF = 2,∠DFE =∠ACB = 45°.
∴AC= ,DF=2 .∠EFB= 90°.
∴AD=DF-AC= .∴点A为DF的中点.
∴EA⊥DF. EA平分∠DEF.
∴∠MAE = 90°.∠AEF = 45°. AE=/2.
∵∠MEB =∠AEF = 45°.∴∠MEA =∠BEF.
(3)如下图所示,过点 B作BE 的垂线交直线EM 于点G.连接AG,BG.
∵∠EBG = 90°,∠BEM = 45°,
∴∠BGE=∠BEM=45°.
∴BE = BG.
∵∠ABC=∠EBG= 90°,∴∠ABG =∠CBE.
又∵BA= BC,∴△ABG≌△CBE.
∴AG = CE = x,∠AGB =∠CEB.
∵∠AGB +∠AGM =∠CEB +∠DEM = 45°.
∴∠AGM =∠DEM,∴AG∥DE.∴DN=DE=π/2.
中考链接
13.(1)图(a)中与△ADE 相似的有△ABD,△ACD,△DCE.
(2)△BDF∽△CED∽△DEF,证明如下:
∵∠B+∠BDF+∠BFD=180°,∠EDF+∠BDF+∠CDE=180°,又∵∠EDF=∠B,∴∠BFD=∠CDE.
∵AB=AC,∴∠B=∠C.∴△BDF∽△CED.
即
又∵∠C=∠EDF,∴△CED∽△DEF.
∴△BDF∽△CED∽△DEF.
(3)如下图所示,连接AD,过 D点作DG⊥EF,DH⊥BF,垂足分别为G、H.
∵AB=AC,D是BC的中点,
在 Rt△ABD中,AD =AB -BD ,即.
∴AD=8.
∵△BDF∽△DEF,∴∠DFB=∠EFD.
∵DH⊥BF,DG⊥EF,∴∠DHF=∠DGF.
又∵DF=DF,∴△DHF≌△DGF,∴DH=DG= .
∴EF=5.
14.(1)/3
(2)如下图所示,过点 P 作PH⊥AB,PG⊥BC,垂足分别为H. G.
∵在矩形ABCD中,∠ABC=90°,∴PH∥BC.
又∵∠ACB=30°,∴∠APH=∠PCG=30°.
由题意可知∠HPE=∠GPF=∠α,
又∵点 P在矩形ABCD 对角线交点上,
(3)变化
证明:过点 P作PH⊥AB,PG⊥BC,垂足分别为 H,G.根据(2),同理可证
又∵AP: PC=1:2
巅峰突破
15.(1)①2.60°;②2;
(2)结论:O O =AO ,O O ⊥AO .
△AO O 经过旋转相似变换A( .45'),得到△ABI,此时.线段 O O 变为线段 BI:
△CIB 经过旋转相似变换 得到△CAO ,此时,线段 BI变为线段AO .
16.(1)DB+DC≥ AD.
(2)BD+ DC≥2AD.
证明:如下图所示,作∠ADE=60°,过点 A 作AE⊥AD交 DE 于点E,连 BE.
在 Rt△ADE中,∠ADE=60°,∴∠AED=30°.若= .在Rt△ABC中.
∵∠EAB+∠BAD=∠CAD+∠BAD=90°.
∴∠EAB=∠CAD.∴△ABE∽△ACD.
则
Rt△ADE中,DE=2AD.
∵BD+BE≥DE,∴BD+/3DC≥2AD.
一、课标导航
课标内容 课标要求 目标层次
相似三角形的综合应用 利用相似三角形的知识解决问题 ★★
二、核心纲要
常见的相似模型如下:
(1)母子型 (2)双垂型 (3)三垂直型
本节重点讲解:模型的应用,相似三角形与其他知识的综合.
三、全能突破
基础演练
1.如图27-2-1 所示,正方形 ABCD 的边长为4,M、N 分别是 BC、CD 上的两个动点,且始终保持 当 时,四边形 ABCN的面积最大.
2.如图27-2-2所示,在等边 中,P 为BC 上一点,D为AC 上一点,且 则△AB 的周长为 .
3.如图27-2-3 所示,在△ABC中,AB=AC= 5,BC= 8,D,E 分别为BC、AB边上一点,
(1)求证:△BDE∽△CAD.
(2)若CD=2,求 BE的长.
(3)设CD=x,AE=y,求 y关于x 的函数关系式,并写出自变量 x的取值范围.
4.如图27-2-4 所示,C 是以AB 为直径的⊙O上一点,过点 O 作OE⊥AC 于点 E,过点 A 作⊙O的切线交OE 的延长线于点F,连接CF 并延长交 BA 的延长线于点 P.
(1)求证:PC是⊙O的切线.
(2)若 AB=4,AP: PC=1:2,求CF的长.
5.如图27-2-5 所示,AB 为⊙O 的直径,BC 切⊙O 于点 B,AC 交⊙O 于点 D,E 为 BC中点.
求证:(1)DE为⊙O的切线.
(2)延长 ED 交 BA 的延长线于 F,若DF=4,AF=2,求 BC的长.
能力提升
6.如图27-2-6所示,已知AB∥EF∥CD,AB=30,CD=50,则 EF的长为 .
7.如图27-2-7所示,在Rt△ABC中,∠ABC 是直角,. ,P 是BC 边上的动点,设.BP=x,若能在 AC 边上找到一点Q,使 则x的取值范围是 .
8.如图27-2-8 所示,正方形 ABCD的边长为10,内部有6个全等的正方形,小正方形的顶点 E、F、G、H分别落在边AD、AB、BC、CD上,则 DE 的长为 .
9.操作:如图 27-2-9 所示,在正方形 ABCD中,P 是CD上一动点(与C、D 不重合),使三角板的直角顶点与点 P 重合,并且一条直角边始终经过点 B,另一直角边与正方形的某一边所在直线交于点 E.
探究:①观察操作结果,哪一个三角形与△BPC 相似,写出你的结论(找出两对即可);并选择其中一组说明理由.
②当点 P 位于CD 的中点时,直接写出①中找到的两对相似三角形的相似比和面积比.
10.操作:如图 27-2-10(a)所示,点O为线段MN 的中点,直线 PQ与MN 相交于点O,请利用图27-2-10(a)画出一对以点 O 为对称中心的全等三角形.
根据上述操作得到的经验完成下列探究活动:
探究一:如图 27-2-10(b)所示,在四边形 ABCD中,AB∥DC,E为BC边的中点,∠BAE=∠EAF,AF 与DC 的延长线相交于点 F. 试探究线段AB 与AF、CF 之间的等量关系,并证明你的结论.
探究二:如图27-2-10(c)所示,DE、BC相交于点E,BA交DE 于点A,且 BE:EC=1:2,∠BAE=∠EDF,CF∥AB.若AB=5,CF=1,求 DF 的长度.
11.如图27-2-11(a)所示,在 Rt△ABC中,∠ACB=90°,CP 平分∠ACB,CP 与AB 交于点D,且 PA
(1)请你过点 P 分别向 AC、BC作垂线,垂足分别为点 E、F,并判断四边形 PECF 的形状.
(2)求证: 为等腰直角三角形.
(3)设 ,试用m、n的代数式表示△ABC的周长.
(4)试探索当边 AC、BC的长度变化时, 的值是否发生变化,若不变,请直接写出这个不变的值,若变化,试说明理由(图27-2-11(b)为备用图).
12.数学课上,张老师给出图27-2-12(a)和下面框中条件:
如图27-2-12(a)所示,两块等腰直角三角板ABC和DEF 有一条边在同一条直线l上,, DEF=90°,AB=1,DE=2.将直线 EB绕点 E 逆时针旋转4 ,交直线 AD 于点M.将图27-2-|12(a)中的三角板 ABC沿直线l向右平移,设C、E两点间的距离为x.
请你和艾思轲同学一起尝试探究下列问题:
(1)①当点C与点 F 重合时,如图27-2-12(b)所示,可得 的值为 ;
②在平移过程中, 的值为 (用含 x的代数式表示).
(2)艾思轲同学将图27-2-12(b)中的三角板 ABC绕点C 逆时针旋转,原题中的其他条件保持不变.当点 A 落在线段 DF 上时,如图 27-2-12(c)所示,请你帮他补全图形,并计算 的值.
(3)艾思轲同学又将图27-2-12(a)中的三角板 ABC 绕点C 逆时针旋转 度,原题中的其他条件保持不变.请你计算 的值(用含x的代数式表示).
中考链接
13如图 27-2-13 所示,在 中,AB=AC,D为BC 的中点,以 D为顶点作∠MDN=∠B.
(1)如图27-2-13(a)所示,当射线 DN 经过点A 时,DM交AC 边于点 E,不添加辅助线,写出图中所有与△ADE 相似的三角形.
(2)如图27-2-13(b)所示,将∠MDN 绕点D 沿逆时针方向旋转,DM、DN分别交线段AC、AB 于 E、F 点(点 E 与点A 不重合),不添加辅助线,写出图中所有的相似三角形,并证明你的结论.
(3)在图27-2-13(b)所示中,若AB=AC=10,BC=12,当△DEF 的面积等于△ABC 的面积的 时,求线段EF的长.
14.(山东临沂)在矩形 ABCD 中,∠ACB =30°,将一块直角三角板的直角顶点 P 放在两对角线AC、BD 的交点处,以点 P 为旋转中心转动三角板,并保证三角板的两直角边分别于边 AB、BC所在的直线相交,交点分别为 E、F.
(1)当 PE⊥AB,PF⊥BC时,如图27-2-14(a)所示,则 的值为 .
(2)现将三角板绕点 P 逆时针旋转α(0°<α<60°)角,如图 27-2-14(b)所示,求 的值.
(3)在(2)的基础上继续旋转,当( ,且使AP: PC=1:2时,如图27-2-14(c)所示, 的值是否变化 证明你的结论.
中小学教育资源及组卷应用平台
巅峰突破
15.在平面内,先将一个多边形以点O为位似中心放大或缩小,使所得多边形与原多边形对应线段的比为 k,并且原多边形上的任一点 P,它的对应点 在线段OP 或其延长线上;接着将所得多边形以点O为旋转中心,逆时针旋转一个角度θ,这种经过缩放和旋转的图形变换叫做旋转相似变换,记为O(k,θ),其中点O叫做旋转相似中心,k叫做相似比,θ叫做旋转角.
(1)填空
①如图 27-2-15(a)所示,将 以点A 为旋转相似中心放大为原来的 2 倍,再逆时针旋转60°,得到 ,这个旋转相似变换记为 A( , );
②如图27-2-15(b)所示,. 是边长为 1cm的等边三角形,将它作旋转相似变换 90),得到 ,则线段 BD的长为 cm.
(2)如图27-2-15(c)所示,分别以锐角三角形 ABC 的三边 AB、BC、CA 为边向外作正方形 ADEB、BF-GC、CHIA,点 分别是这三个正方形的对角线交点,试分别利用, 与 与 之间的关系,运用旋转相似变换的知识说明线段( 与 之间的关系.
16.(1)如图27-2-16(a)所示,在四边形 ABDC中,. 猜想 与 的11大小关系(直接写出结论)
(2)如图27-2-16(b)所示,在四边形 ABDC 中,. 猜想 2AD 与 的大小关系并证明.
基础演练
1.2 2.9
3.(1)∵AB=AC,∴∠B=∠C.∵ ∠ADE+∠BDE=∠ADB =∠C+∠CAD,∠ADE=∠C,
∴∠BDE =∠CAD. ∴△BDE∽△CAD.
(2)由(1)得DB=△D.∵AB=AC= 5,BC= 8,CD=2,
∴DB=BC-CD=6.
(3)由已知BE=5-y;BD=8-x.∵△BDE∽△CAD.
即
4.(1)连接OC,如下图所示 .∵ OE⊥AC,∴AE=CE.
∴FA=FC.
∴∠FAC=∠FCA.∵OA=OC,∴∠OAC=∠OCA.
∴ ∠OAC+∠FAC=∠OCA+∠FCA. 即∠FAO=∠FCO.
∵FA与⊙O相切,且AB是⊙O的直径,∴ FA⊥AB.
∴∠FCO=∠FAO=90°.∴ PC 是⊙O的切线.
(2)∵∠PCO=90°,即∠ACO +∠ACP =90°.
又∵∠BCO+∠ACO=90°,∴∠ACP=∠BCO.
∵BO=CO.∴∠BCO=∠B.∴∠ACP=∠B.
∵∠P公共角,∴△PCA∽△PBC.
∵FA与⊙O相切,∴∠FAO=90°.∴ OF∥BC.
∴∠AOF=∠ABC.∴△ABC∽△FOA.
∴AF=1.∴CF=1.
5.(1)如下图所示,连接OD、BD.
∵在⊙O 中,OD=OB,∴∠1=∠2.
∵AB是⊙O的直径,∴∠ADB=∠CDB=90°.
∵E为BC中点,
∴∠3=∠4.∵BC切⊙O于点B,∴∠EBA=90°.
∴∠1+∠3=∠2+∠4=90°,
即∠ODE=90°.∴OD⊥DE.∵点 D 在⊙O上,∴DE是⊙O的切线.
(2)∵OD⊥DE,∴∠FDO=90°.
设( ,
解得r=3.
∴OA=OD=3,FB=8.
∵∠F=∠F,∠FDO=∠FBE=90°.
∵E为BC中点,∴BC=2BE=12.
能力提升
6. 7.3≤x≤4 8.2
9.分两种情况:
①如图(a)所示,
∵∠BPE=90°.
∴∠BPC+∠DPE=90°,
又∠BPC+∠PBC=90°,
∴∠PBC=∠DPE,
又∠C=∠D=90°.
∴△BPC∽△PED.
如图(b)所示,同理可证△BPC∽△BEP∽△PEC.
②如图(a)所示,
∵△BPC∽△PED,
∴△PED与△BPC 的周长比等于对应边的比,即 PD与BC 的比,
∵点P位于CD 的中点,
∴PD与BC 的比为1:2,
∴△PED与△BPC的周长比1:2,面积比1:4.
如图(b)所示,
∵△BPC∽△BEP,∴△BEP与△BPC 的周长比等于对应边的比,即 BP与BC的比.
∵点 P位于CD的中点,设 BC=2k,则 PC=k,BP=/5k,
∴BP与BC的比为 :2,
△BEP与△BPC的周长比为 :2.
△BEP与△BPC的面积比为5:4.
同理:△PCE∽△BPC,周长比1:2,面积比1:4.
10.图略;
探究一:
结论:AB=AF+CF.
证明:分别延长AE、DF 交于点M,∵E为BC 的中点,
∴BE=CE.∵AB∥CD.∴∠BAE=∠M.
∵∠AEB=∠MEC,∴△ABE≌△MCE.∴AB=MC.
又∵∠BAE=∠EAF,∴∠M=∠EAF.∴MF=AF.
又∵MC=MF+CF,∴AB=AF+CF.
探究二:
分别延长 DE、CF交于点G,
∵AB∥CF,∴∠B=∠C,∠BAE=∠G.
∴△ABE∽△GCE∴△C=BC.
∵FC=1,∴GF=9.
又∵∠BAE=∠EDF.∴∠G=∠EDF.∴GF=DF.
∴DF=9.
11.(1)过点 P分别作 PE⊥AC、PF⊥CB,垂足分别为E、F,∵∠ACB=90°,PE⊥AC,PF⊥CB,∴四边形 PECF 是矩形.
又∵点 P 在∠ACB 的角平分线上,且 PE⊥AC、PF⊥CB,∴PE=PF.
∴四边形 PECF 是正方形.
(2)在 Rt△AEP和Rt△BFP中,
∵PE=PF,PA=PB,
∴Rt△AEP≌Rt△BFP.∴∠APE=∠BPF.
∵∠EPF= 90°,∴∠APB= 90°.∵PA=PB.
∴△PAB是等腰直角三角形.
(3)如下图所示,在 Rt△PAB中,∠APB=90°,PA=PB,
由(2)可知,Rt△AEP≌Rt△BFP,可得 AE=BF,CE=CF,
∴CA+CB=CE+EA+CB=CE+CF=2CE.
又
的周长为:AB+BC+
(4)不变
如下图所示.∵∠1=∠2=∠3=∠4=45°,且∠ADC=∠PDB.
∴△ADC∽△PDB.∴≌D=△FB.(即
同理可得,△CDB∽△ADP,得到
又 PA= PB,则①+②得:
12.(1)①1.② .
(2)连接AE,补全图形如下图所示.
∵△ABC 和△DEF 是等腰直角三角形,AB = 1. DE
= 2.
∴BC= 1,EF = 2,∠DFE =∠ACB = 45°.
∴AC= ,DF=2 .∠EFB= 90°.
∴AD=DF-AC= .∴点A为DF的中点.
∴EA⊥DF. EA平分∠DEF.
∴∠MAE = 90°.∠AEF = 45°. AE=/2.
∵∠MEB =∠AEF = 45°.∴∠MEA =∠BEF.
(3)如下图所示,过点 B作BE 的垂线交直线EM 于点G.连接AG,BG.
∵∠EBG = 90°,∠BEM = 45°,
∴∠BGE=∠BEM=45°.
∴BE = BG.
∵∠ABC=∠EBG= 90°,∴∠ABG =∠CBE.
又∵BA= BC,∴△ABG≌△CBE.
∴AG = CE = x,∠AGB =∠CEB.
∵∠AGB +∠AGM =∠CEB +∠DEM = 45°.
∴∠AGM =∠DEM,∴AG∥DE.∴DN=DE=π/2.
中考链接
13.(1)图(a)中与△ADE 相似的有△ABD,△ACD,△DCE.
(2)△BDF∽△CED∽△DEF,证明如下:
∵∠B+∠BDF+∠BFD=180°,∠EDF+∠BDF+∠CDE=180°,又∵∠EDF=∠B,∴∠BFD=∠CDE.
∵AB=AC,∴∠B=∠C.∴△BDF∽△CED.
即
又∵∠C=∠EDF,∴△CED∽△DEF.
∴△BDF∽△CED∽△DEF.
(3)如下图所示,连接AD,过 D点作DG⊥EF,DH⊥BF,垂足分别为G、H.
∵AB=AC,D是BC的中点,
在 Rt△ABD中,AD =AB -BD ,即.
∴AD=8.
∵△BDF∽△DEF,∴∠DFB=∠EFD.
∵DH⊥BF,DG⊥EF,∴∠DHF=∠DGF.
又∵DF=DF,∴△DHF≌△DGF,∴DH=DG= .
∴EF=5.
14.(1)/3
(2)如下图所示,过点 P 作PH⊥AB,PG⊥BC,垂足分别为H. G.
∵在矩形ABCD中,∠ABC=90°,∴PH∥BC.
又∵∠ACB=30°,∴∠APH=∠PCG=30°.
由题意可知∠HPE=∠GPF=∠α,
又∵点 P在矩形ABCD 对角线交点上,
(3)变化
证明:过点 P作PH⊥AB,PG⊥BC,垂足分别为 H,G.根据(2),同理可证
又∵AP: PC=1:2
巅峰突破
15.(1)①2.60°;②2;
(2)结论:O O =AO ,O O ⊥AO .
△AO O 经过旋转相似变换A( .45'),得到△ABI,此时.线段 O O 变为线段 BI:
△CIB 经过旋转相似变换 得到△CAO ,此时,线段 BI变为线段AO .
16.(1)DB+DC≥ AD.
(2)BD+ DC≥2AD.
证明:如下图所示,作∠ADE=60°,过点 A 作AE⊥AD交 DE 于点E,连 BE.
在 Rt△ADE中,∠ADE=60°,∴∠AED=30°.若= .在Rt△ABC中.
∵∠EAB+∠BAD=∠CAD+∠BAD=90°.
∴∠EAB=∠CAD.∴△ABE∽△ACD.
则
Rt△ADE中,DE=2AD.
∵BD+BE≥DE,∴BD+/3DC≥2AD.
同课章节目录
