【备课参考】沪科版八年级数学上册教学设计:15-4 角的平分线
文档属性
| 名称 | 【备课参考】沪科版八年级数学上册教学设计:15-4 角的平分线 |

|
|
| 格式 | zip | ||
| 文件大小 | 137.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2015-10-26 00:18:42 | ||
图片预览

文档简介
15.4 角的平分线
教学目标
【知识与技能】
1.会阐述角平分线的性质定理及其逆定理.
2.会应用角平分线定理及其逆定理证明两条线段相等或两个角相等.
【过程与方法】
1.经历探索角平分线作法的过程,进一步体验轴对称的特点,发展空间观察能力.
2.探索角平分线定理,培养学生认真探究、积极思考的能力.
【情感 、态度与价值观】
1.体验数学与生活的联系,发展学生的空间观念和审美观.
2.活动与探究的过程可以更大程度地激发学生学习的主动性和积极性,使学生具有一些初步研究问题的能力.
重点难点
【重点】
角平分线的性质定理及其逆定理.
【难点】
理解并证明角平分线的性质定理及其逆定理.
教学过程
一、创设情境,导入新知
师:同学们知道怎样作出角的平分线吗
生1:可以通过折纸得到一个角的平分线.
生2:也可以用量角器来画一个角的平分线.
师:下面我们来学习用尺规作图的方法作出∠AOB的平分线.
作法:
1.以O为圆心、任意长为半径圆弧分别交OA、OB于点M、N,如图(1).
( http: / / www.21cnjy.com )
2.分别以点M、N为圆心,以大于MN长为半径在角的内部画弧交于点P,如图(2).
3.作射线OP,则OP为所要求作的∠AOB的平分线,如图(3).
师:通过上面的作图,启发我们可以用尺规完成:“经过一点作已知直线的垂线.”
由于这一点可能在直线上或直线外,这个作图要分两种情况:
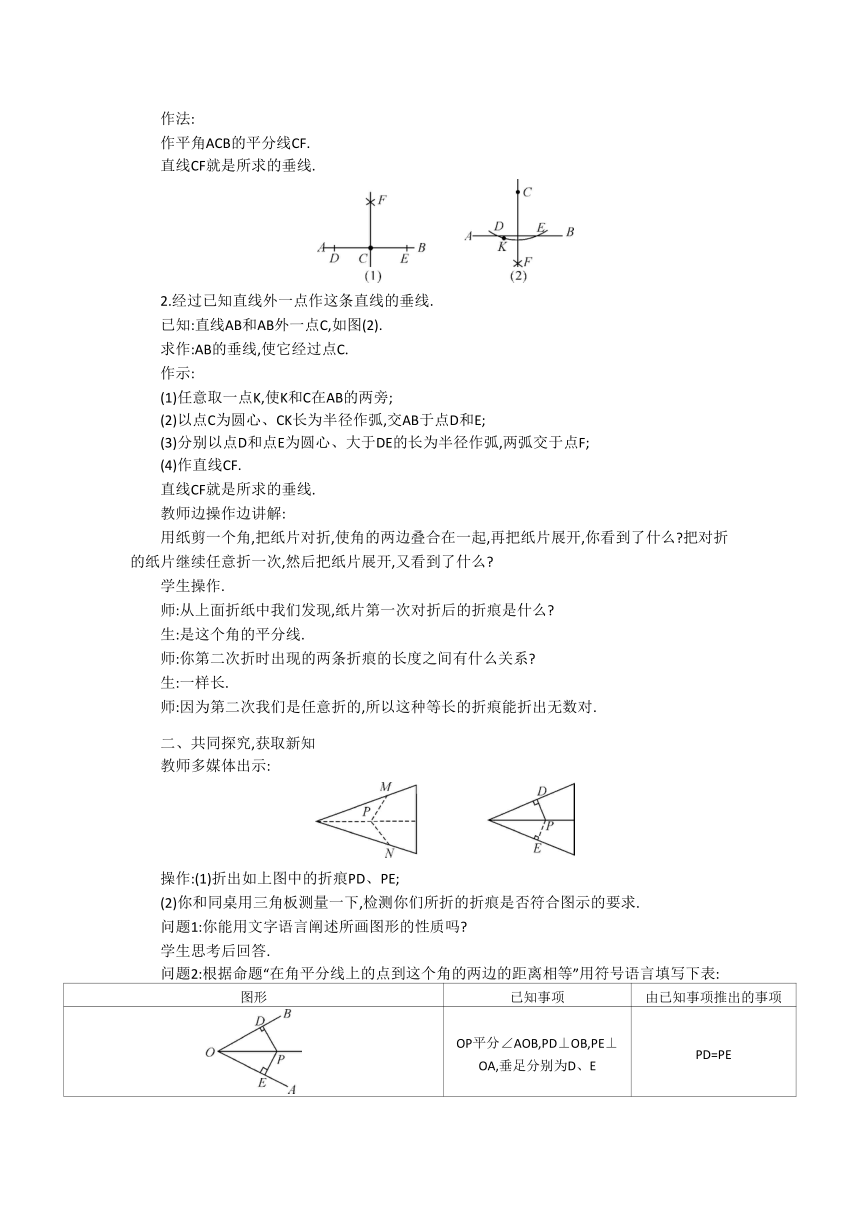
1.经过已知直线上的一点作这条直线的垂线.
已知:直线AB和AB上一点C,如图(1).
求作:AB的垂线,使它经过点C.
作法:
作平角ACB的平分线CF.
直线CF就是所求的垂线.
( http: / / www.21cnjy.com )
2.经过已知直线外一点作这条直线的垂线.
已知:直线AB和AB外一点C,如图(2).
求作:AB的垂线,使它经过点C.
作示:
(1)任意取一点K,使K和C在AB的两旁;
(2)以点C为圆心、CK长为半径作弧,交AB于点D和E;
(3)分别以点D和点E为圆心、大于DE的长为半径作弧,两弧交于点F;
(4)作直线CF.
直线CF就是所求的垂线.
教师边操作边讲解:
用纸剪一个角,把纸片对折,使角的两边叠合在一起,再把纸片展开,你看到了什么 把对折的纸片继续任意折一次,然后把纸片展开,又看到了什么
学生操作.
师:从上面折纸中我们发现,纸片第一次对折后的折痕是什么
生:是这个角的平分线.
师:你第二次折时出现的两条折痕的长度之间有什么关系
生:一样长.
师:因为第二次我们是任意折的,所以这种等长的折痕能折出无数对.
二、共同探究,获取新知
教师多媒体出示:
( http: / / www.21cnjy.com )
操作:(1)折出如上图中的折痕PD、PE;
(2)你和同桌用三角板测量一下,检测你们所折的折痕是否符合图示的要求.
问题1:你能用文字语言阐述所画图形的性质吗
学生思考后回答.
问题2:根据命题“在角平分线上的点到这个角的两边的距离相等”用符号语言填写下表:
图形 已知事项 由已知事项推出的事项
( http: / / www.21cnjy.com ) OP平分∠AOB,PD⊥OB,PE⊥OA,垂足分别为D、E PD=PE
(推证定理1)
问题3:根据下表中的图形和已知事项,猜想由已知事项可推出的事项,并用符号语言填写下表:
图形 已知事项 由已知事项推出的事项
( http: / / www.21cnjy.com ) DE⊥AB,BC⊥AC,垂足分别为E、C,DE=DC. ∠DAE=∠DAC
问题4:用文字语言表述上表中的已知事项和由已知事项推出的事项.
(推证定理2)
三、练习新知,加深理解
师:下面我们接着来探讨上面的问题3.
教师多媒体出示:
(1)∵AD平分∠BAC,
DC⊥AC,DE⊥AB,(已知)
∴DC=DE.( )
(2)∵DC⊥AC,DE⊥AB,DC=DE,(已知)
∴点D在∠BAC的平分线上.( )
学生思考后抢答,教师板书.
第1个括号中填“角平分线上任意一点到角的两边的距离相等”,第2个括号中填“到角的两边距离相等的点在这个角的平分线上”.
教师多媒体出示:
【例1】 已知:如图所示,∠C=∠C'=90°,AC=AC'.
( http: / / www.21cnjy.com )
求证:(1)∠ABC=∠ABC';(2)BC=BC'.(要求不用三角形全等判定)
学生思考后交流讨论.
教师找一名学生板演,其余同学在下面做,然后集体订正.
证明:(1)∵∠C=∠C'=90°,(已知)
∴AC⊥BC,AC'⊥BC'.(垂直的定义)
又∵AC=AC',(已知)
∴点A在∠CBC'的角平分线上.(到一个角的两边的距离相等的点,在这个角的平分线上)
∴∠ABC=∠ABC'.
(2)∵∠C=∠C',∠ABC=∠ABC',
∴180°-(∠C+∠ABC)=180°-(∠C'+∠ABC').(三角形内角和定理)
即∠BAC=∠ABC'.
∵BC⊥AC,BC'⊥AC',
∴BC=BC'.(角平分线上的点到这个角的两边的距离相等)
【例2】 已知:如图,△ABC中,∠B、∠C的平分线BE、CF相交于点P.
求证:AP平分∠BAC.
( http: / / www.21cnjy.com )
证明:过点P分别作PM⊥BC、PN⊥AC、PQ⊥AB,垂足分别为M、N、Q.
∵BE是∠B的平分线,点P在BE上,(已知)
∴PQ=PM.(角平分线上任意一点到角的两边的距离相等)
同理PN=PM.
∴PN=PQ.(等量代换)
∴AP平分∠BAC.(到角的两边距离相等的点在这个角的平分线上)
四、课堂小结
师:你今天学习了什么知识 有什么新的收获
学生回答,教师点评.
教学反思
本节课开头设计的折纸和画一画的活动,旨在 ( http: / / www.21cnjy.com )丰富学生对角平分线性质的感知,有利于学生借助直观图从而准确地用文字语言揭示角平分线的性质.由于部分学生常常把“过角平分线上一点向角两边画垂线段”与“过角平分线上一点画角平分线的垂线”混为一谈,因此设计操作(1)、(2),为学生能正确画出符合要求的图形,从直观上以及三角板的正确使用上都作了恰当的铺垫,同时也为定理1的推理论证作准备.通过学生自己动后操作、自己推导、自己发现,从而得到角平分线的性质定理及其逆定理,充分发挥学生的探究意识,使学生在学习中体验并掌握合作交流的学习方法,同时进一步锻炼学生的数学语言表达能力,能写出规范的证明过程.
教学目标
【知识与技能】
1.会阐述角平分线的性质定理及其逆定理.
2.会应用角平分线定理及其逆定理证明两条线段相等或两个角相等.
【过程与方法】
1.经历探索角平分线作法的过程,进一步体验轴对称的特点,发展空间观察能力.
2.探索角平分线定理,培养学生认真探究、积极思考的能力.
【情感 、态度与价值观】
1.体验数学与生活的联系,发展学生的空间观念和审美观.
2.活动与探究的过程可以更大程度地激发学生学习的主动性和积极性,使学生具有一些初步研究问题的能力.
重点难点
【重点】
角平分线的性质定理及其逆定理.
【难点】
理解并证明角平分线的性质定理及其逆定理.
教学过程
一、创设情境,导入新知
师:同学们知道怎样作出角的平分线吗
生1:可以通过折纸得到一个角的平分线.
生2:也可以用量角器来画一个角的平分线.
师:下面我们来学习用尺规作图的方法作出∠AOB的平分线.
作法:
1.以O为圆心、任意长为半径圆弧分别交OA、OB于点M、N,如图(1).
( http: / / www.21cnjy.com )
2.分别以点M、N为圆心,以大于MN长为半径在角的内部画弧交于点P,如图(2).
3.作射线OP,则OP为所要求作的∠AOB的平分线,如图(3).
师:通过上面的作图,启发我们可以用尺规完成:“经过一点作已知直线的垂线.”
由于这一点可能在直线上或直线外,这个作图要分两种情况:
1.经过已知直线上的一点作这条直线的垂线.
已知:直线AB和AB上一点C,如图(1).
求作:AB的垂线,使它经过点C.
作法:
作平角ACB的平分线CF.
直线CF就是所求的垂线.
( http: / / www.21cnjy.com )
2.经过已知直线外一点作这条直线的垂线.
已知:直线AB和AB外一点C,如图(2).
求作:AB的垂线,使它经过点C.
作示:
(1)任意取一点K,使K和C在AB的两旁;
(2)以点C为圆心、CK长为半径作弧,交AB于点D和E;
(3)分别以点D和点E为圆心、大于DE的长为半径作弧,两弧交于点F;
(4)作直线CF.
直线CF就是所求的垂线.
教师边操作边讲解:
用纸剪一个角,把纸片对折,使角的两边叠合在一起,再把纸片展开,你看到了什么 把对折的纸片继续任意折一次,然后把纸片展开,又看到了什么
学生操作.
师:从上面折纸中我们发现,纸片第一次对折后的折痕是什么
生:是这个角的平分线.
师:你第二次折时出现的两条折痕的长度之间有什么关系
生:一样长.
师:因为第二次我们是任意折的,所以这种等长的折痕能折出无数对.
二、共同探究,获取新知
教师多媒体出示:
( http: / / www.21cnjy.com )
操作:(1)折出如上图中的折痕PD、PE;
(2)你和同桌用三角板测量一下,检测你们所折的折痕是否符合图示的要求.
问题1:你能用文字语言阐述所画图形的性质吗
学生思考后回答.
问题2:根据命题“在角平分线上的点到这个角的两边的距离相等”用符号语言填写下表:
图形 已知事项 由已知事项推出的事项
( http: / / www.21cnjy.com ) OP平分∠AOB,PD⊥OB,PE⊥OA,垂足分别为D、E PD=PE
(推证定理1)
问题3:根据下表中的图形和已知事项,猜想由已知事项可推出的事项,并用符号语言填写下表:
图形 已知事项 由已知事项推出的事项
( http: / / www.21cnjy.com ) DE⊥AB,BC⊥AC,垂足分别为E、C,DE=DC. ∠DAE=∠DAC
问题4:用文字语言表述上表中的已知事项和由已知事项推出的事项.
(推证定理2)
三、练习新知,加深理解
师:下面我们接着来探讨上面的问题3.
教师多媒体出示:
(1)∵AD平分∠BAC,
DC⊥AC,DE⊥AB,(已知)
∴DC=DE.( )
(2)∵DC⊥AC,DE⊥AB,DC=DE,(已知)
∴点D在∠BAC的平分线上.( )
学生思考后抢答,教师板书.
第1个括号中填“角平分线上任意一点到角的两边的距离相等”,第2个括号中填“到角的两边距离相等的点在这个角的平分线上”.
教师多媒体出示:
【例1】 已知:如图所示,∠C=∠C'=90°,AC=AC'.
( http: / / www.21cnjy.com )
求证:(1)∠ABC=∠ABC';(2)BC=BC'.(要求不用三角形全等判定)
学生思考后交流讨论.
教师找一名学生板演,其余同学在下面做,然后集体订正.
证明:(1)∵∠C=∠C'=90°,(已知)
∴AC⊥BC,AC'⊥BC'.(垂直的定义)
又∵AC=AC',(已知)
∴点A在∠CBC'的角平分线上.(到一个角的两边的距离相等的点,在这个角的平分线上)
∴∠ABC=∠ABC'.
(2)∵∠C=∠C',∠ABC=∠ABC',
∴180°-(∠C+∠ABC)=180°-(∠C'+∠ABC').(三角形内角和定理)
即∠BAC=∠ABC'.
∵BC⊥AC,BC'⊥AC',
∴BC=BC'.(角平分线上的点到这个角的两边的距离相等)
【例2】 已知:如图,△ABC中,∠B、∠C的平分线BE、CF相交于点P.
求证:AP平分∠BAC.
( http: / / www.21cnjy.com )
证明:过点P分别作PM⊥BC、PN⊥AC、PQ⊥AB,垂足分别为M、N、Q.
∵BE是∠B的平分线,点P在BE上,(已知)
∴PQ=PM.(角平分线上任意一点到角的两边的距离相等)
同理PN=PM.
∴PN=PQ.(等量代换)
∴AP平分∠BAC.(到角的两边距离相等的点在这个角的平分线上)
四、课堂小结
师:你今天学习了什么知识 有什么新的收获
学生回答,教师点评.
教学反思
本节课开头设计的折纸和画一画的活动,旨在 ( http: / / www.21cnjy.com )丰富学生对角平分线性质的感知,有利于学生借助直观图从而准确地用文字语言揭示角平分线的性质.由于部分学生常常把“过角平分线上一点向角两边画垂线段”与“过角平分线上一点画角平分线的垂线”混为一谈,因此设计操作(1)、(2),为学生能正确画出符合要求的图形,从直观上以及三角板的正确使用上都作了恰当的铺垫,同时也为定理1的推理论证作准备.通过学生自己动后操作、自己推导、自己发现,从而得到角平分线的性质定理及其逆定理,充分发挥学生的探究意识,使学生在学习中体验并掌握合作交流的学习方法,同时进一步锻炼学生的数学语言表达能力,能写出规范的证明过程.
