人教版八年级数学上册13.1.2线段垂直平分线的性质教学设计
文档属性
| 名称 | 人教版八年级数学上册13.1.2线段垂直平分线的性质教学设计 |
|
|
| 格式 | doc | ||
| 文件大小 | 75.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-04-18 12:25:15 | ||
图片预览

文档简介
线段垂直平分线的性质
教学目标 1.理解线段垂直平分线的性质. 2.能运用线段垂直平分线的性质解决有关问题. 3.能用尺规作线段的垂直平分线.了解作图的道理.
教学重点教学难点 线段垂直平分线的性质.运用线段垂直平分线的性质及尺规作图.
学情分析 从心理特征来说,初中阶段的学生逻辑思维从经验型逐步向理论型发展,观察能力,推理能力和想象能力也随着迅速发展。但同时,这一阶段的学生好动,注意力易分散,爱发表见解,希望得到老师的表扬,所以在教学中应抓住这些特点,一方面运用直观生动几何画板演示,引发学生的兴趣,使他们的注意力始终集中在课堂上;另一方面,要创造条件和机会,让学生发表见解,发挥学生学习的主动性。认知状况来说,学生在此之前已经学习了轴对称图形,对线段的垂直平分线已经有了初步的认识,这为顺利完成本节课的教学任务打下了基础,所以教学中应具体生动,深入浅出的让学生发现知识.
教学方法 探究发现法,小组合作.
教学手段 多媒体 几何画板 电子白板 高拍仪 微视频等辅助教学
教学过程
问题与情境 师生行为 设计意图
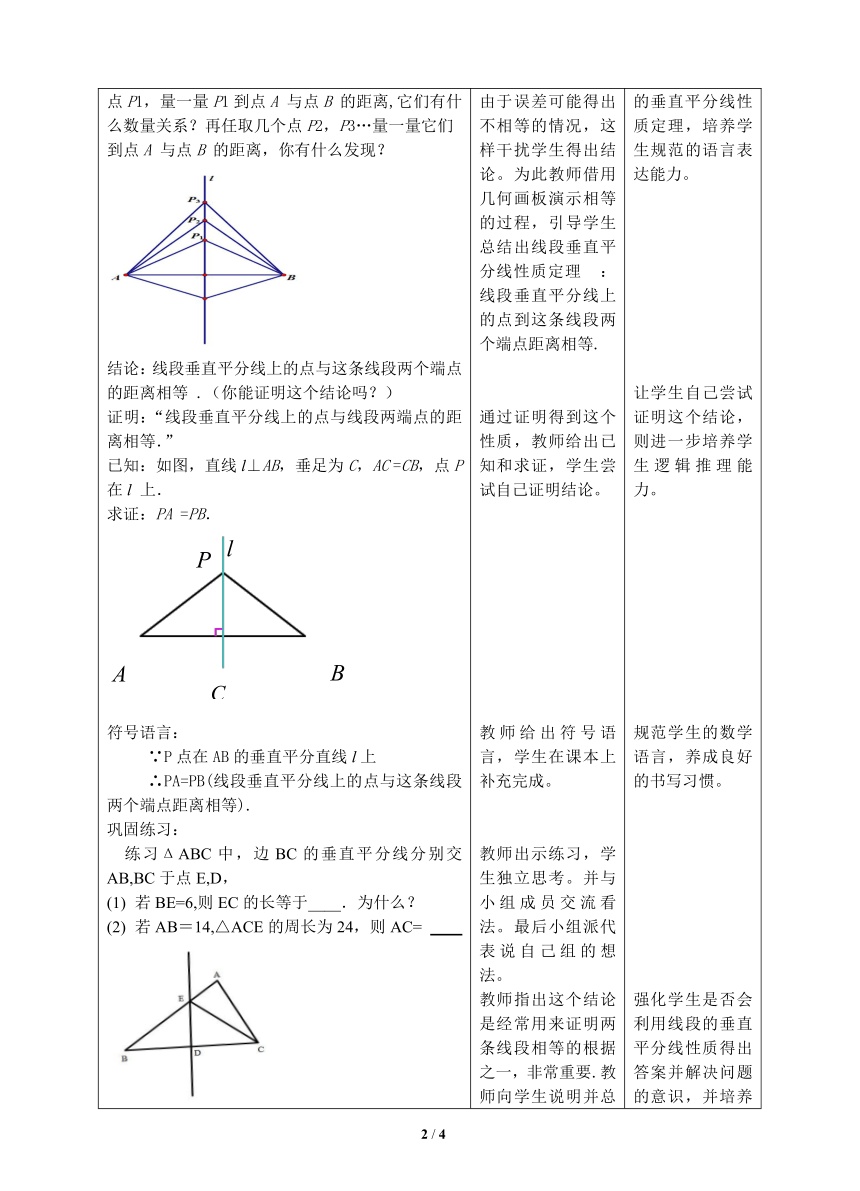
[活动1] 复习旧知:线段是不是轴对称图形?(生易回答是)它的对称轴是什么?垂直平分线的定义是什么? 教师提出问题,学生回答. 复习上节轴对称图形和对称轴,为本节课内容做铺垫.
[活动2] 探究新知画图:直线l 垂直平分线段AB,在直线l上任取一点P1,量一量P1到点A 与点B 的距离,它们有什么数量关系?再任取几个点P2,P3…量一量它们到点A 与点B 的距离,你有什么发现?结论:线段垂直平分线上的点与这条线段两个端点的距离相等 .(你能证明这个结论吗?)证明:“线段垂直平分线上的点与线段两端点的距离相等.”已知:如图,直线l⊥AB,垂足为C,AC =CB,点P 在l 上.求证:PA =PB.符号语言: ∵P点在AB的垂直平分直线l上 ∴PA=PB(线段垂直平分线上的点与这条线段两个端点距离相等). 巩固练习: 练习ΔABC中,边BC的垂直平分线分别交AB,BC于点E,D,若BE=6,则EC的长等于____.为什么?若AB=14,△ACE的周长为24,则AC= 反过来,与一条线段两个端点距离相等的点,在这条线段的垂直平分线上吗?如果PA=PB,那么p点是否在线段的垂直平分线上呢?你能证明吗?已知:PA=PB,求证:点P在线段AB的垂直平分线上。反过来:与一条线段两个端点距离相等的点,在这条线段的垂直平分线上.符号语言:∵PA=PB(已知),∴点P在AB的垂直平分线上 两个定理是什么关系? 教师追问:你能再找一些到线段AB 两端点的距离相等的点吗? 能找到多少个到线段AB 两端点距离相等的点?这些点能组成什么几何图形? 线段垂直平分线是到线段两端点的距离相等的所有点的集合,这条线包含了满足条件的所有的点。【活动3】演示思考:尺规作图:做线段的垂直平分线怎样作线段AB 的垂直平分线呢?作法:如图.(1)分别以点A,B 为圆心,以大于 AB的长为半径作弧,两弧相交于C,D 两点;(2)作直线CD. CD 就是所求作的直线. 这种作法的依据是什么? 这种作图方法还有哪些作用? 例1 :课本62页例1 学生动手画图,并测量PA,PB的长度,由于误差可能得出不相等的情况,这样干扰学生得出结论。为此教师借用几何画板演示相等的过程,引导学生总结出线段垂直平分线性质定理 : 线段垂直平分线上的点到这条线段两个端点距离相等.通过证明得到这个性质,教师给出已知和求证,学生尝试自己证明结论。教师给出符号语言,学生在课本上补充完成。教师出示练习,学生独立思考。并与小组成员交流看法。最后小组派代表说自己组的想法。教师指出这个结论是经常用来证明两条线段相等的根据之一,非常重要.教师向学生说明并总结证明两条线段相等的方法。教师出示问题,并借助几何画板演示。学生独立思考,并小组讨论,辅助线的做法是关键,必要时由老师引导学生得出答案,完成证明过程。学生完成符号语言的书写,归纳两个定理的关系,教师指出在线段AB 的垂直平分线l 上的点与A,B 的距离都相等;反过来,与A,B 的距离相等的点都在直线l上,所以直线l 可以看成与两点A、B 的距离相等的所有点的集合.教师用问题串提问学生,学生作答。教师一步步在黑板上演示作图过程,并让学生观察并思考问题。最后在练习本上完成作图。学生动手完成练习(课上或课下) 学生在演示思考环节基础上,观看微视频 学习过直线外一点作这条直线的垂线(时间充裕一起分析作图原理,时间不够让学生回家反复观看视频并思考作图原理) 让学生总结线段的垂直平分线性质定理,培养学生规范的语言表达能力。让学生自己尝试证明这个结论,则进一步培养学生逻辑推理能力。规范学生的数学语言,养成良好的书写习惯。强化学生是否会利用线段的垂直平分线性质得出答案并解决问题的意识,并培养学生表达自己的意见的习惯。教师给出辅助线的做法,旨在降低证明的难度,通过线段的垂直平分线的性质定理让学生感受几何中的互逆命题的关系。总结线段垂直平分线的性质定理的过程,培养了学生的归纳总结和逆向思维能力。抛给学生问题串旨在降低作图院里的难度,为学生搭台阶,让学生掌握作直线的垂直平分线的方法,并弄清楚原理。通过尺规作图,培养学生的动手实践能力以及分析解决问题的能力。
【活动4】 课堂小结(1)本节课学习了哪些内容?(2)学习本节课后,你有哪些收获?哪些疑难之处? 教师与学生一起回顾本节课所学的主要内容。 通过小结,使学生梳理本节课所学内容和研究方法,培养学生总结归纳能力和概括能力。
【活动5】布置作业一、云测练上观看学习“过直线外一点作垂线”微课;二、教科书62页练习1、2;习题13.1第6题。选作第9题。 为下节课重点做铺垫让学生独立完成课后作业,有能力的同学完成选做题。 跟踪了解学生对本节课的知识掌握情况,同时给不同层次的学生锻炼的机会
l
A
B
P
C
C
P
B
A
B
A
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
1 / 4
教学目标 1.理解线段垂直平分线的性质. 2.能运用线段垂直平分线的性质解决有关问题. 3.能用尺规作线段的垂直平分线.了解作图的道理.
教学重点教学难点 线段垂直平分线的性质.运用线段垂直平分线的性质及尺规作图.
学情分析 从心理特征来说,初中阶段的学生逻辑思维从经验型逐步向理论型发展,观察能力,推理能力和想象能力也随着迅速发展。但同时,这一阶段的学生好动,注意力易分散,爱发表见解,希望得到老师的表扬,所以在教学中应抓住这些特点,一方面运用直观生动几何画板演示,引发学生的兴趣,使他们的注意力始终集中在课堂上;另一方面,要创造条件和机会,让学生发表见解,发挥学生学习的主动性。认知状况来说,学生在此之前已经学习了轴对称图形,对线段的垂直平分线已经有了初步的认识,这为顺利完成本节课的教学任务打下了基础,所以教学中应具体生动,深入浅出的让学生发现知识.
教学方法 探究发现法,小组合作.
教学手段 多媒体 几何画板 电子白板 高拍仪 微视频等辅助教学
教学过程
问题与情境 师生行为 设计意图
[活动1] 复习旧知:线段是不是轴对称图形?(生易回答是)它的对称轴是什么?垂直平分线的定义是什么? 教师提出问题,学生回答. 复习上节轴对称图形和对称轴,为本节课内容做铺垫.
[活动2] 探究新知画图:直线l 垂直平分线段AB,在直线l上任取一点P1,量一量P1到点A 与点B 的距离,它们有什么数量关系?再任取几个点P2,P3…量一量它们到点A 与点B 的距离,你有什么发现?结论:线段垂直平分线上的点与这条线段两个端点的距离相等 .(你能证明这个结论吗?)证明:“线段垂直平分线上的点与线段两端点的距离相等.”已知:如图,直线l⊥AB,垂足为C,AC =CB,点P 在l 上.求证:PA =PB.符号语言: ∵P点在AB的垂直平分直线l上 ∴PA=PB(线段垂直平分线上的点与这条线段两个端点距离相等). 巩固练习: 练习ΔABC中,边BC的垂直平分线分别交AB,BC于点E,D,若BE=6,则EC的长等于____.为什么?若AB=14,△ACE的周长为24,则AC= 反过来,与一条线段两个端点距离相等的点,在这条线段的垂直平分线上吗?如果PA=PB,那么p点是否在线段的垂直平分线上呢?你能证明吗?已知:PA=PB,求证:点P在线段AB的垂直平分线上。反过来:与一条线段两个端点距离相等的点,在这条线段的垂直平分线上.符号语言:∵PA=PB(已知),∴点P在AB的垂直平分线上 两个定理是什么关系? 教师追问:你能再找一些到线段AB 两端点的距离相等的点吗? 能找到多少个到线段AB 两端点距离相等的点?这些点能组成什么几何图形? 线段垂直平分线是到线段两端点的距离相等的所有点的集合,这条线包含了满足条件的所有的点。【活动3】演示思考:尺规作图:做线段的垂直平分线怎样作线段AB 的垂直平分线呢?作法:如图.(1)分别以点A,B 为圆心,以大于 AB的长为半径作弧,两弧相交于C,D 两点;(2)作直线CD. CD 就是所求作的直线. 这种作法的依据是什么? 这种作图方法还有哪些作用? 例1 :课本62页例1 学生动手画图,并测量PA,PB的长度,由于误差可能得出不相等的情况,这样干扰学生得出结论。为此教师借用几何画板演示相等的过程,引导学生总结出线段垂直平分线性质定理 : 线段垂直平分线上的点到这条线段两个端点距离相等.通过证明得到这个性质,教师给出已知和求证,学生尝试自己证明结论。教师给出符号语言,学生在课本上补充完成。教师出示练习,学生独立思考。并与小组成员交流看法。最后小组派代表说自己组的想法。教师指出这个结论是经常用来证明两条线段相等的根据之一,非常重要.教师向学生说明并总结证明两条线段相等的方法。教师出示问题,并借助几何画板演示。学生独立思考,并小组讨论,辅助线的做法是关键,必要时由老师引导学生得出答案,完成证明过程。学生完成符号语言的书写,归纳两个定理的关系,教师指出在线段AB 的垂直平分线l 上的点与A,B 的距离都相等;反过来,与A,B 的距离相等的点都在直线l上,所以直线l 可以看成与两点A、B 的距离相等的所有点的集合.教师用问题串提问学生,学生作答。教师一步步在黑板上演示作图过程,并让学生观察并思考问题。最后在练习本上完成作图。学生动手完成练习(课上或课下) 学生在演示思考环节基础上,观看微视频 学习过直线外一点作这条直线的垂线(时间充裕一起分析作图原理,时间不够让学生回家反复观看视频并思考作图原理) 让学生总结线段的垂直平分线性质定理,培养学生规范的语言表达能力。让学生自己尝试证明这个结论,则进一步培养学生逻辑推理能力。规范学生的数学语言,养成良好的书写习惯。强化学生是否会利用线段的垂直平分线性质得出答案并解决问题的意识,并培养学生表达自己的意见的习惯。教师给出辅助线的做法,旨在降低证明的难度,通过线段的垂直平分线的性质定理让学生感受几何中的互逆命题的关系。总结线段垂直平分线的性质定理的过程,培养了学生的归纳总结和逆向思维能力。抛给学生问题串旨在降低作图院里的难度,为学生搭台阶,让学生掌握作直线的垂直平分线的方法,并弄清楚原理。通过尺规作图,培养学生的动手实践能力以及分析解决问题的能力。
【活动4】 课堂小结(1)本节课学习了哪些内容?(2)学习本节课后,你有哪些收获?哪些疑难之处? 教师与学生一起回顾本节课所学的主要内容。 通过小结,使学生梳理本节课所学内容和研究方法,培养学生总结归纳能力和概括能力。
【活动5】布置作业一、云测练上观看学习“过直线外一点作垂线”微课;二、教科书62页练习1、2;习题13.1第6题。选作第9题。 为下节课重点做铺垫让学生独立完成课后作业,有能力的同学完成选做题。 跟踪了解学生对本节课的知识掌握情况,同时给不同层次的学生锻炼的机会
l
A
B
P
C
C
P
B
A
B
A
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
1 / 4
