山东省泰安市岱岳区八上数学(青岛版)学案:5.4 平行线的性质定理和判定定理
文档属性
| 名称 | 山东省泰安市岱岳区八上数学(青岛版)学案:5.4 平行线的性质定理和判定定理 |
|
|
| 格式 | zip | ||
| 文件大小 | 71.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2015-10-25 00:00:00 | ||
图片预览


文档简介
课题 5.4 平行线的性质定理和判定定理 课型 新授
内容 八上教科书166---168页 主备人
学习目标 1.进一步熟悉证明的基本步骤和书写格式2.会根据“两直线平行,同位角相等”证明平行线的其它性质定理3.正确区别平行线的判定和性质.
重点 平行线的性质定理和判定定理的应用.
难点 推理过程的规范化表达和灵活应用.。
学前预习案
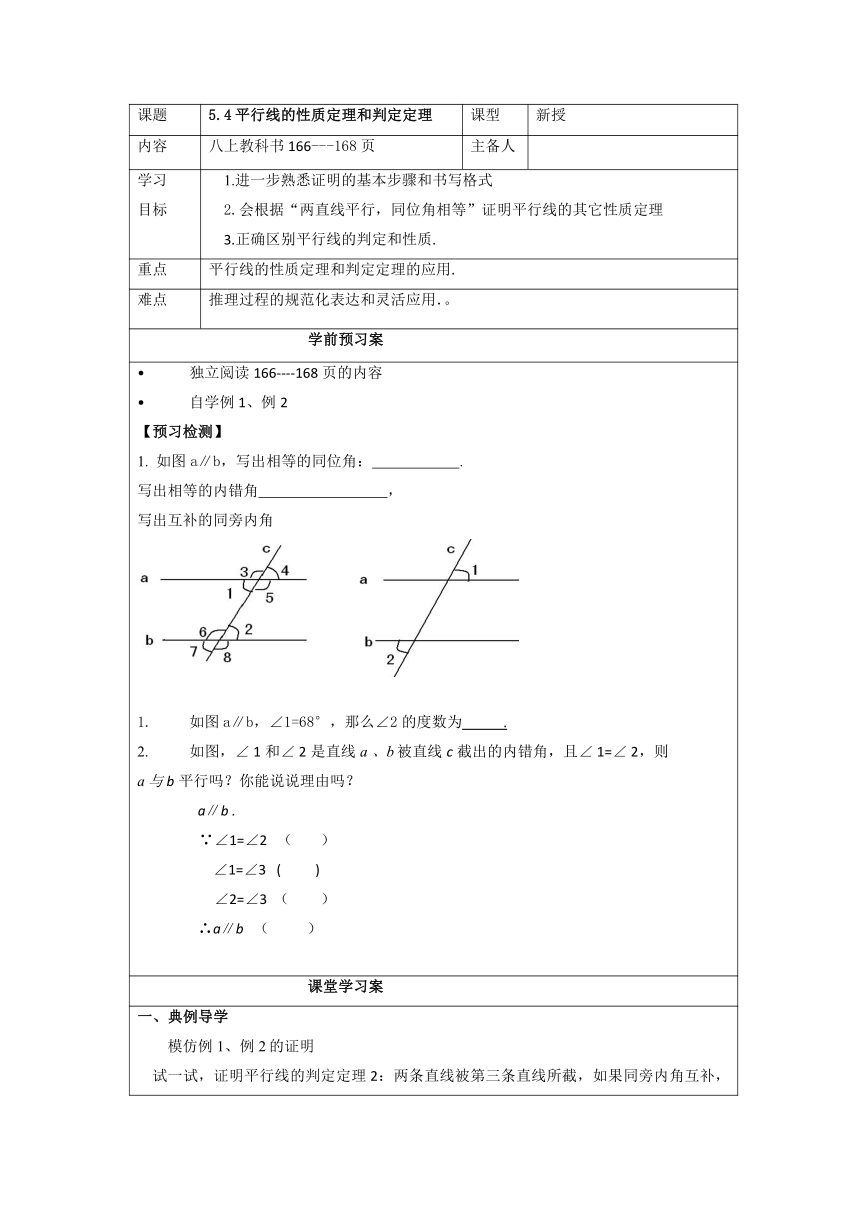
独立阅读166----168页的内容自学例1、例2【预习检测】1. 如图a∥b,写出相等的同位角: . 写出相等的内错角 ,写出互补的同旁内角 如图a∥b,∠1=68°,那么∠2的度数为 . 如图,∠ 1和∠ 2是直线a 、b被直线c截出的内错角,且∠ 1=∠ 2,则a与b平行吗?你能说说理由吗?a∥b .∵∠1=∠2 ( )∠1=∠3 ( )∠2=∠3 ( )∴a∥b ( )
课堂学习案
一、典例导学模仿例1、例2的证明 试一试,证明平行线的判定定理2: ( http: / / www.21cnjy.com )两条直线被第三条直线所截,如果同旁内角互补,那么这两条直线平行。(简称:同旁内角互补,两条直线平行)。二、交流与发现命题1: 同位角相等,两直线平行命题2: 两直线平行,同位角相等观察这两个命题,你有什么发现? 两个命题中,如果第一个命题的______是第二个命题的______,而第一个命题的______又是第二个命题的______,那么这两个命题叫做互逆命题。其中一个命题称为原命题 ,那么另一个命题叫做它的逆命题。练习题:说出下列命题的逆命题,并与同学交流:①轴对称图形是等腰三角形; ②等角的补角相等;③直角三角形的两个锐角互余; ④正方形的4个角都是直角. 如果一个定理的逆命题也是真命题,那么这个逆命题就是原来定理的-------------------.三、自主应用1.已知:如图∠1=∠2,∠3=1000, 求∠4的度数. 2.已知:如图a∥b,b∥c. 求证:a∥c.你证明的命题用文字叙述为__________________________________________;可以简单地叙述为____________________________________,3、下列命题,它们的逆命题是否是真命题.(1).全等三角形的对应角相等; ( )(2).直角三角形两锐角互余; ( )(3).直角都相等; ( )(4).等腰三角形的两底角相等. ( )四、当堂巩固1.如图所示AB∥CD,∠C=1150,∠A= 250, 则∠E的度数为( )A.700 B.800 C.900 D.10002. .如图所示a∥b,∠1=1050,∠2=1400 则∠3的度数为( )A.750 B.650 C.550 D.5003.如图所示AB∥CD,AC⊥BC,∠BAC=650, 则∠BCD=_________度. 4、如图:⑴∠1=∠A,则GC∥AB,依据是 ;⑵∠3=∠B,则EF∥AB,依据是 ;⑶∠2+∠A=180°,则DC∥AB,依据是 ;⑷∠1=∠4,则GC∥EF,依据是 ;⑸∠C+∠B=180°,则GC∥AB,依据是 ;⑹∠4=∠A,则EF∥AB,依据是 .五、课堂小结,作业布置作业、课本:随堂练习 1,2
课后拓展案
如图,AB∥CD .求证:∠A+∠C+∠E=1800.
内容 八上教科书166---168页 主备人
学习目标 1.进一步熟悉证明的基本步骤和书写格式2.会根据“两直线平行,同位角相等”证明平行线的其它性质定理3.正确区别平行线的判定和性质.
重点 平行线的性质定理和判定定理的应用.
难点 推理过程的规范化表达和灵活应用.。
学前预习案
独立阅读166----168页的内容自学例1、例2【预习检测】1. 如图a∥b,写出相等的同位角: . 写出相等的内错角 ,写出互补的同旁内角 如图a∥b,∠1=68°,那么∠2的度数为 . 如图,∠ 1和∠ 2是直线a 、b被直线c截出的内错角,且∠ 1=∠ 2,则a与b平行吗?你能说说理由吗?a∥b .∵∠1=∠2 ( )∠1=∠3 ( )∠2=∠3 ( )∴a∥b ( )
课堂学习案
一、典例导学模仿例1、例2的证明 试一试,证明平行线的判定定理2: ( http: / / www.21cnjy.com )两条直线被第三条直线所截,如果同旁内角互补,那么这两条直线平行。(简称:同旁内角互补,两条直线平行)。二、交流与发现命题1: 同位角相等,两直线平行命题2: 两直线平行,同位角相等观察这两个命题,你有什么发现? 两个命题中,如果第一个命题的______是第二个命题的______,而第一个命题的______又是第二个命题的______,那么这两个命题叫做互逆命题。其中一个命题称为原命题 ,那么另一个命题叫做它的逆命题。练习题:说出下列命题的逆命题,并与同学交流:①轴对称图形是等腰三角形; ②等角的补角相等;③直角三角形的两个锐角互余; ④正方形的4个角都是直角. 如果一个定理的逆命题也是真命题,那么这个逆命题就是原来定理的-------------------.三、自主应用1.已知:如图∠1=∠2,∠3=1000, 求∠4的度数. 2.已知:如图a∥b,b∥c. 求证:a∥c.你证明的命题用文字叙述为__________________________________________;可以简单地叙述为____________________________________,3、下列命题,它们的逆命题是否是真命题.(1).全等三角形的对应角相等; ( )(2).直角三角形两锐角互余; ( )(3).直角都相等; ( )(4).等腰三角形的两底角相等. ( )四、当堂巩固1.如图所示AB∥CD,∠C=1150,∠A= 250, 则∠E的度数为( )A.700 B.800 C.900 D.10002. .如图所示a∥b,∠1=1050,∠2=1400 则∠3的度数为( )A.750 B.650 C.550 D.5003.如图所示AB∥CD,AC⊥BC,∠BAC=650, 则∠BCD=_________度. 4、如图:⑴∠1=∠A,则GC∥AB,依据是 ;⑵∠3=∠B,则EF∥AB,依据是 ;⑶∠2+∠A=180°,则DC∥AB,依据是 ;⑷∠1=∠4,则GC∥EF,依据是 ;⑸∠C+∠B=180°,则GC∥AB,依据是 ;⑹∠4=∠A,则EF∥AB,依据是 .五、课堂小结,作业布置作业、课本:随堂练习 1,2
课后拓展案
如图,AB∥CD .求证:∠A+∠C+∠E=1800.
同课章节目录
- 第1章 全等三角形
- 1.1 全等三角形
- 1.2 怎样判定三角形全等
- 1.3 尺规作图
- 第2章 图形的轴对称
- 2.1 图形的轴对称
- 2.2 轴对称的基本性质
- 2.3 轴对称图形
- 2.4 线段的垂直平分线
- 2.5 角平分线的性质
- 2.6 等腰三角形
- 第3章 分式
- 3.1 分式的基本性质
- 3.2 分式的约分
- 3.3 分式的乘法与除法
- 3.4 分式的通分
- 3.5 分式的加法与减法
- 3.6 比和比例
- 3.7 可化为一元一次方程的分式方程
- 第4章 数据分析
- 4.1 加权平均数
- 4.2 中位数
- 4.3 众数
- 4.4 数据的离散程度
- 4.5 方差
- 4.6 用计算器计算平均数和方差
- 第5章 几何证明初步
- 5.1 定义与命题
- 5.2 为什么要证明
- 5.3 什么是几何证明
- 5.4 平行线的性质定理和判定定理
- 5.5 三角形内角和定理
- 5.6 几何证明举例
