2015-2016山东省泰安市岱岳区八上数学(青岛版)学案:5.3什么是几何证明
文档属性
| 名称 | 2015-2016山东省泰安市岱岳区八上数学(青岛版)学案:5.3什么是几何证明 |

|
|
| 格式 | zip | ||
| 文件大小 | 48.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2015-10-26 00:00:00 | ||
图片预览

文档简介
课题 5.3什么是几何证明 课型 新授
内容 八上教科书161---163页 主备人 a
学习目标 了解基本事实、证明、定理的含义,知道本书中基本事实;了解并会用几何的三个证明步骤。
重点 掌握证明的格式
难点 会用几何的三个证明步骤
学前预习案
一.回顾引入 “如果两个角是对顶角,那么这两个角相等”,这是对顶角的性质,你能证明它的正确性吗?二、独立阅读161---163页的内容,约6分钟,完成以下内容:知识点一:基本事实:1. ____________________________________________________叫做基本事实.2.下列基本事实也作为公理:(1)_ ____________.(2)______________ ______________.(3)______________________ _____.(4)________________________ ____.(5) (6) (7)______________________ (8)________________________ ____. 3. _____________________________________________________叫做证明.知识点二:定理_______________________________________________________叫做定理.
课堂学习案
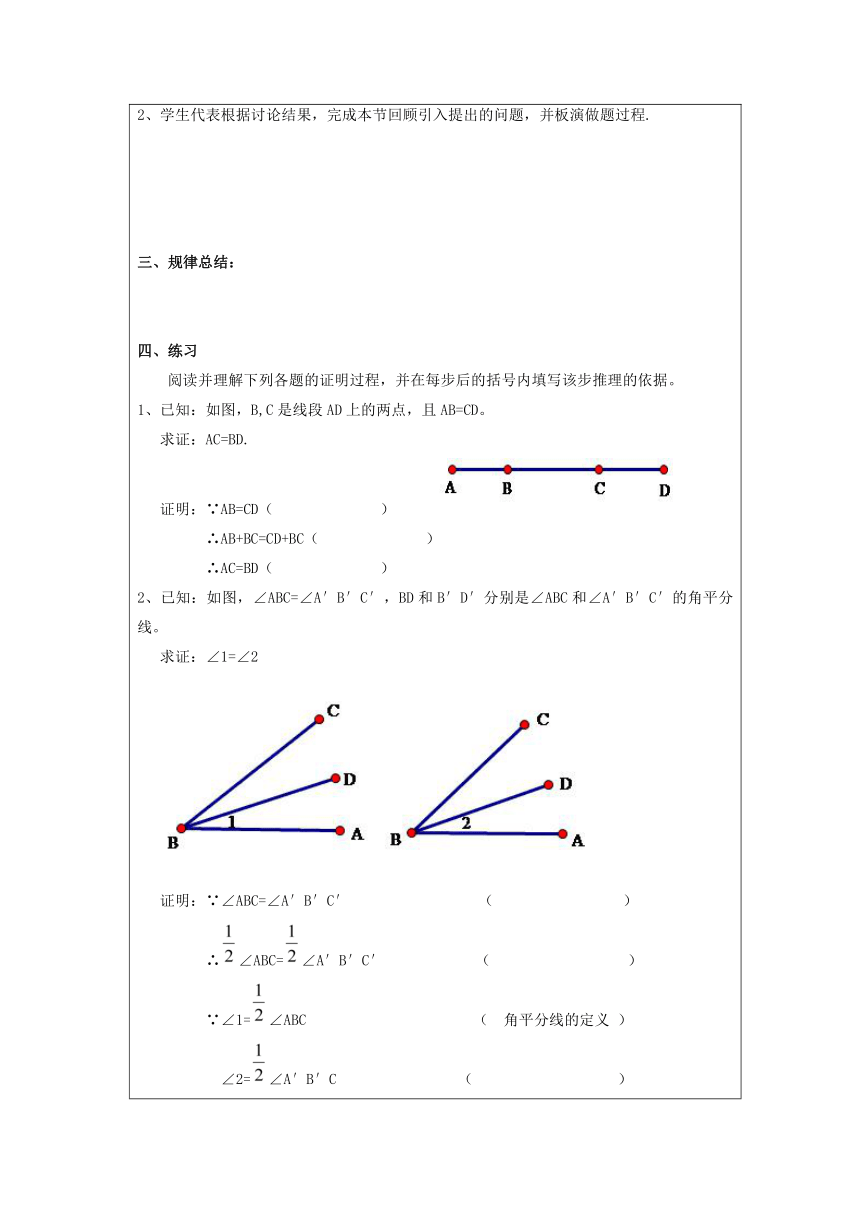
导入新课二、合作探究活动一:1、以小组为单位,讨论交流如何解决本节回顾引入提出的问题。2、学生代表根据讨论结果,完成本节回顾引入提出的问题,并板演做题过程.三、规律总结: 四、练习阅读并理解下列各题的证明过程,并在每步后的括号内填写该步推理的依据。1、已知:如图,B,C是线段AD上的两点,且AB=CD。求证:AC=BD.证明:∵AB=CD( ) ∴AB+BC=CD+BC( ) ∴AC=BD( )2、已知:如图,∠ABC=∠A′B′C′,BD和B′D′分别是∠ABC和∠A′B′C′的角平分线。求证:∠1=∠2证明:∵∠ABC=∠A′B′C′ ( ) ∴∠ABC=∠A′B′C′ ( ) ∵∠1=∠ABC ( 角平分线的定义 )∠2=∠A′B′C ( )∴∠1=∠2 ( )活动二、典例解析(小组内讨论交流,画出图形,写出已知、求证,证明)例1 求证:同角的余角相等。总结:几何证明的步骤有哪些?(1)____________________________;(2)____________________________;(3)____________________________.知识应用,巩固训练:1、求证:同角的补角相等。 2、求证:等角的余角相等。小结反思:交流本节收获与不足: 。五、当堂检测1、阅读并理解下列各题的证明过程,并在每步后的括号内填写该步推理的依据。已知:如图,点B在直线AC上,∠ABE和∠DBC互为余角。求证:DB⊥EB.证明:∵∠ABE和∠DBC互为余角( ) ∴∠ABE+∠DBC=90°( ) ∵点B在直线AC上( ) ∴∠ABC=180°( )∵∠ABE+∠EBD+∠DBC=∠ABC(角的和的定义)∴∠ABE+∠EBD+∠DBC=180°( )∴∠EBD=90°( )∴DE⊥EB( )2、已知:如图,直线AB,CD相交于点O,且∠AOC是直角。 求证:∠COB,∠BOD, ∠DOA都是直角。六、课堂小结:本课你有什么收获?七、布置作业: 必做题:习题2、 3 选做题:4
课后拓展案
已知:如图AB∥CD,∠E=∠F.求证:∠1=∠2.
内容 八上教科书161---163页 主备人 a
学习目标 了解基本事实、证明、定理的含义,知道本书中基本事实;了解并会用几何的三个证明步骤。
重点 掌握证明的格式
难点 会用几何的三个证明步骤
学前预习案
一.回顾引入 “如果两个角是对顶角,那么这两个角相等”,这是对顶角的性质,你能证明它的正确性吗?二、独立阅读161---163页的内容,约6分钟,完成以下内容:知识点一:基本事实:1. ____________________________________________________叫做基本事实.2.下列基本事实也作为公理:(1)_ ____________.(2)______________ ______________.(3)______________________ _____.(4)________________________ ____.(5) (6) (7)______________________ (8)________________________ ____. 3. _____________________________________________________叫做证明.知识点二:定理_______________________________________________________叫做定理.
课堂学习案
导入新课二、合作探究活动一:1、以小组为单位,讨论交流如何解决本节回顾引入提出的问题。2、学生代表根据讨论结果,完成本节回顾引入提出的问题,并板演做题过程.三、规律总结: 四、练习阅读并理解下列各题的证明过程,并在每步后的括号内填写该步推理的依据。1、已知:如图,B,C是线段AD上的两点,且AB=CD。求证:AC=BD.证明:∵AB=CD( ) ∴AB+BC=CD+BC( ) ∴AC=BD( )2、已知:如图,∠ABC=∠A′B′C′,BD和B′D′分别是∠ABC和∠A′B′C′的角平分线。求证:∠1=∠2证明:∵∠ABC=∠A′B′C′ ( ) ∴∠ABC=∠A′B′C′ ( ) ∵∠1=∠ABC ( 角平分线的定义 )∠2=∠A′B′C ( )∴∠1=∠2 ( )活动二、典例解析(小组内讨论交流,画出图形,写出已知、求证,证明)例1 求证:同角的余角相等。总结:几何证明的步骤有哪些?(1)____________________________;(2)____________________________;(3)____________________________.知识应用,巩固训练:1、求证:同角的补角相等。 2、求证:等角的余角相等。小结反思:交流本节收获与不足: 。五、当堂检测1、阅读并理解下列各题的证明过程,并在每步后的括号内填写该步推理的依据。已知:如图,点B在直线AC上,∠ABE和∠DBC互为余角。求证:DB⊥EB.证明:∵∠ABE和∠DBC互为余角( ) ∴∠ABE+∠DBC=90°( ) ∵点B在直线AC上( ) ∴∠ABC=180°( )∵∠ABE+∠EBD+∠DBC=∠ABC(角的和的定义)∴∠ABE+∠EBD+∠DBC=180°( )∴∠EBD=90°( )∴DE⊥EB( )2、已知:如图,直线AB,CD相交于点O,且∠AOC是直角。 求证:∠COB,∠BOD, ∠DOA都是直角。六、课堂小结:本课你有什么收获?七、布置作业: 必做题:习题2、 3 选做题:4
课后拓展案
已知:如图AB∥CD,∠E=∠F.求证:∠1=∠2.
同课章节目录
- 第1章 全等三角形
- 1.1 全等三角形
- 1.2 怎样判定三角形全等
- 1.3 尺规作图
- 第2章 图形的轴对称
- 2.1 图形的轴对称
- 2.2 轴对称的基本性质
- 2.3 轴对称图形
- 2.4 线段的垂直平分线
- 2.5 角平分线的性质
- 2.6 等腰三角形
- 第3章 分式
- 3.1 分式的基本性质
- 3.2 分式的约分
- 3.3 分式的乘法与除法
- 3.4 分式的通分
- 3.5 分式的加法与减法
- 3.6 比和比例
- 3.7 可化为一元一次方程的分式方程
- 第4章 数据分析
- 4.1 加权平均数
- 4.2 中位数
- 4.3 众数
- 4.4 数据的离散程度
- 4.5 方差
- 4.6 用计算器计算平均数和方差
- 第5章 几何证明初步
- 5.1 定义与命题
- 5.2 为什么要证明
- 5.3 什么是几何证明
- 5.4 平行线的性质定理和判定定理
- 5.5 三角形内角和定理
- 5.6 几何证明举例
