2016届山东省泰安市岱岳区九上数学(青岛版)学案:2.5 解直角三角形的应用(2课时)
文档属性
| 名称 | 2016届山东省泰安市岱岳区九上数学(青岛版)学案:2.5 解直角三角形的应用(2课时) |  | |
| 格式 | zip | ||
| 文件大小 | 171.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2015-10-26 14:38:21 | ||
图片预览




文档简介
课题 2.5 解直角三角形的应用(第一课时) 课型 新授
内容 九下教科书53---57页 主备人
学习目标 1.明确仰角、俯角的概念,并能将之灵活应用于实际生活;2.能从实际问题中抽象出几何模型,并能借助计算器解决问题;3.运用三角比的有关知识来解决实际应用问题.
重点 运用三角比的有关知识来解决实际应用问题.
难点 从实际问题中抽象出恰当的几何模型,用三角比的有关知识来解决.
学前预习案
预习课本P53—P55 请完成下列问题 ①结合2—12示意图会画出铅垂线、仰角、俯角、水平线、视线的示意图;②根据例2的实际问题写出已知条件和结论。运用学过的数学方法,画出适应的解直角三角形的模型。③结合例1,写出已知和求解。
课堂学习案
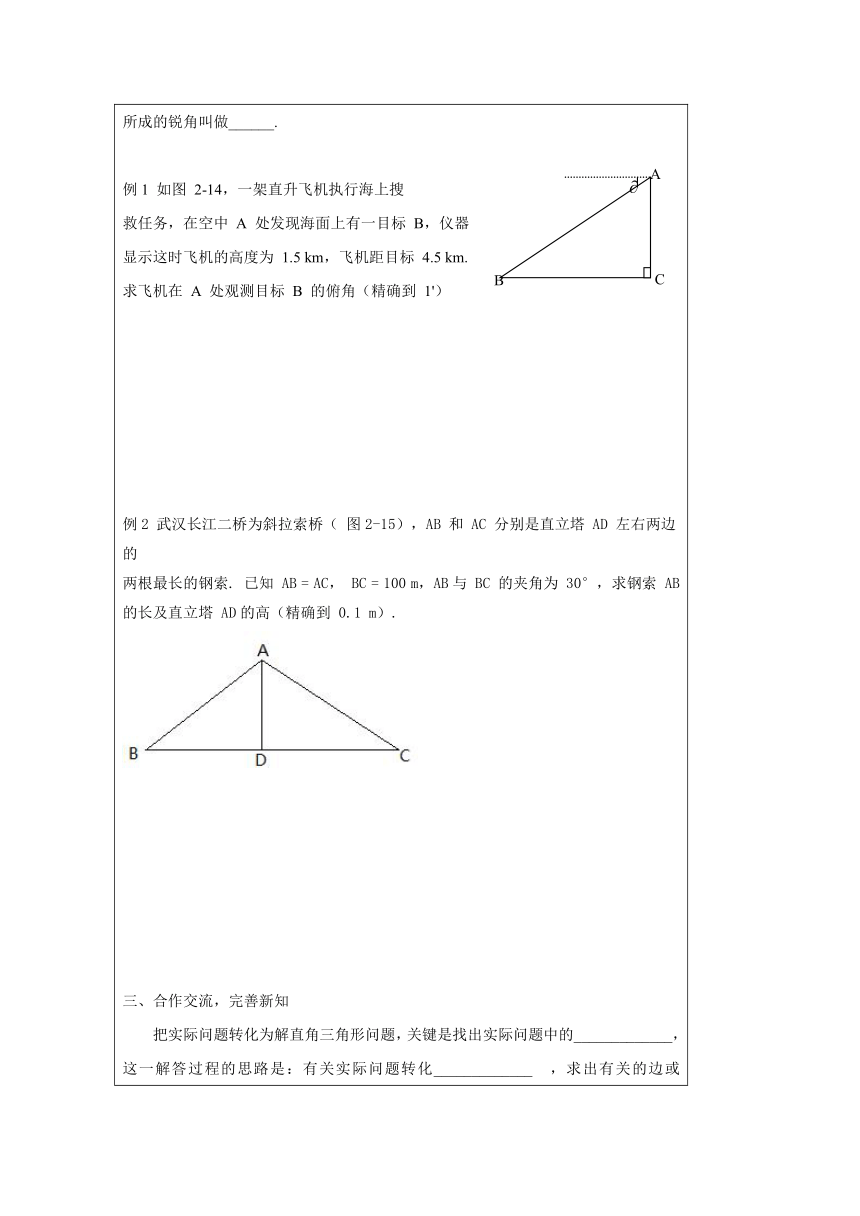
一、创设情境,导入新课东方明珠塔是上海市的一个标志性建筑. 为了测量东方明珠塔的高度,小亮和同学们在距离东方明珠塔 200 m 处的地面上,安放高 1.20 m 的测角仪支架,测得东方明珠塔顶的仰角为 60°48' . 根据测量的结果,小亮画了一张示意图(图 2-11),其中 AB 表示东方明珠塔,DC 为测角仪的支架,DC = 1.20 m,CB= 200 m,∠ADE = 60°48' .利用上述数据,你能求出 AB 的长吗?与同学交流.二、自主探究,归纳新知1.读一读课本54页小资料:在实际测量中 ( http: / / www.21cnjy.com ),从低处观测高处的目标时,_________与_________所成的锐角叫做_________,从高处观测低处的目标时,_______与________所成的锐角叫做______.例1 如图 2-14,一架直升飞机执行海上搜救任务,在空中 A 处发现海面上有一目标 B,仪器显示这时飞机的高度为 1.5 km,飞机距目标 4.5 km.求飞机在 A 处观测目标 B 的俯角(精确到 1')例2 武汉长江二桥为斜拉索桥( 图2-15),AB 和 AC 分别是直立塔 AD 左右两边的两根最长的钢索. 已知 AB = AC, ( http: / / www.21cnjy.com )BC = 100 m,AB与 BC 的夹角为 30°,求钢索 AB 的长及直立塔 AD的高(精确到 0.1 m).合作交流,完善新知把实际问题转化为解直角三角形问题,关键是找 ( http: / / www.21cnjy.com )出实际问题中的_____________,这一解答过程的思路是:有关实际问题转化_____________ ,求出有关的边或 得出问题答案。四、精讲点拨,深化新知如图,厂房屋顶人字架的跨度为10米,上弦AB=BD,∠A=260,求中柱BC和上弦AB的长.(精确到0.01米)五、当堂训练,巩固新知1、如图,小明想测量塔CD的高度。他在A处仰望塔顶,测得仰角为45゜,再往塔的方向前进50m至B处,测得仰角为60゜,那么该塔有多高?(小明的身高忽略不计,结果精确到1m)2、 一颗大树在一次强烈的地震中于C处折断倒下,树顶落在地面B处,测得B处与树的底端A相距25米,∠ABC=24°①求大树折倒下部分BC的长度。(精确到1米)六、当堂检测,布置作业1、一灯柱AB被一钢缆CD ( http: / / www.21cnjy.com )固定,CD与地面成40 夹角,且DB=5m,在C点上方2m处加固另一条钢缆ED,那么钢缆ED的长度为多少?(结果精确到0、01m)2、(1) 从地面上C、D两处看山顶A ( http: / / www.21cnjy.com ),仰角分别是30°和45°,从山顶A看地面上的D处时,则俯角是__________d度。若BD=m米,则山高AB=________米,山顶A距C的距离AC=_____________米. ( http: / / www.21cnjy.com )(2)在坡屋顶的设计图中AB=AC,屋顶的宽度l为10米,坡角(为35°,则坡屋顶的高度h为______________米。
课后拓展案
如图河对岸有水塔AB.在C处测得塔顶的仰角为30°,向塔前进12m到达D,在D处测得A的仰角为45°,求塔高.
课题 2.5 解直角三角形(第二课时) 课型 新授
内容 九下教科书56---57页 主备人 张小勇
学习目标 进一歩掌握解直角三角形的方法。能熟练地应用解直角三角形的知识解决有关航海的实际问题。
重点 重点:熟练掌握方位角的概念,掌握特殊三角比
难点 难点:熟练掌握解直角三角形的基本方法
学前预习案
1、下图,用连线将左边表示的方向与右边表示点的字母连接起来。 ( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com )2、如图,一艘轮船航行到B处时,灯 ( http: / / www.21cnjy.com )塔A在船的北偏东60°的方向,轮船从B处向正东方向行驶2400m到达C处,此时灯塔A在船的正北方向,求C处与灯塔A的距离(精确到1m)。
课堂学习案
一、创设情境,导入新课如图,一船从A点出发,沿北偏东方向航行12海里到达B点,然后又沿南偏东方向航行16海里到达C点,那么从C点再航行多远才能直接返回出发点A(精确到0.1海里) 自主探究,归纳新知1、如图所示,某船从点向正东方向航行,在处望见灯塔在东北方向,前进到处望见灯塔在北偏西方向,又航行了半小时到处,望见灯塔恰在西北方向,若船速为每小时海里,求,两点间距离.合作交流,完善新知2.如图,海关某缉私艇巡逻到达处时,接到情报,在处北偏西方向的处发现一艘可疑船只,正以的速度向正东方向前进,上级命令对可疑船只进行检查,该艇立即沿北偏西的方向快速前进,经过的航行,正好在处截住可疑船只,求该艇的速度.(结果保留到整数)四、精讲点拨,深化新知如图,在港口的正东15海里处有一观测站,一艘货船从处向正北方向航行,当货船航行到处时,从观测站测得货船的方向为北偏西,0.5h后,货船到这处,此时从处测得货船的方向为北偏西.求货船航行的速度(精确到1海里,).五、当堂训练,巩固新知1.海中有一个小岛,它的周围8海里内有暗礁,渔船跟踪鱼群由西向东航行,在点测得小岛在北偏东,航行12海里到达点,这时小岛在北偏东,如果渔船不改变方向航行,继续向东捕捞,有没有触礁的危险?请说明理由.当堂检测,布置作业入夏以来,松花江哈尔滨段水位不断下 ( http: / / www.21cnjy.com )降,达到历史最低水位,一条船在松花江某水段自西向东沿直线航行,在A处测得航标C在北偏东60°方向上,前进100米到达B处,又测得航标C在北偏东45°方向上,如图,在以航标C为圆心,120米长为半径的圆形区域内有浅滩,如果这条船继续前进,是否有被浅滩阻碍的危险?
课后拓展案
2.如图,一艘渔船正以每小时的速度由西向东航行,在处看见小岛在船的北偏东方向上,后,渔船行至处,此时看见小岛在船的北偏东方向上.若以小岛的中心周围的范围内是危险区,问:这艘渔船继续向东航行是否有进入危险区的可能?
课题 2.5 解直角三角形的应用(第三课时) 课型 新授
内容 九下教科书58页 主备人
学习目标 1.认识坡角、坡度,并能结合实际标准角度。2.能应用解直角三角形的知识解决实际问题
重点 直角三角形的解法
难点 三角比在解直角三角形中的灵活运用
学前预习案
1、阅读课本58页中有关坡度的内容,说一说什么是坡角,什么是坡度或坡比,坡度与坡角的正切有什么关系 请把重点知识写在下面._______________________________________________________________________________________________________________________________________________________________________________________________________________2、看例4的解答过程,你知道如何构造直角三角形来解决实际问题吗?需要做什么辅助线?
课堂学习案
一、创设情境,导入新课二、自主探究,归纳新知例4、某地计划在河流的上游 ( http: / / www.21cnjy.com )修建一条拦水大坝,大坝的横断面ABCD是梯形(如图),坝顶宽BC=6米,坝高25米,迎水坡AB的坡度i=1:3,背水坡CD的坡度i=1:2.5.(1)求斜坡AB和CD的长(精确到0.01米);(2)求拦水大坝的底面AD的宽.三、精讲点拨,深化新知1、某校教学楼后面紧邻着一个土坡,坡上面是一块平地,如图所示,,斜坡长22m,坡角,为了防止山体滑坡,保障安全,学校决定对该土坡进行改造.地质人员勘测,当坡角不超过时,可确保山体不滑坡.(1)求改造前坡顶与地面的距离的长(精确到0.1m);(2)为确保安全,学校计划改造时保持坡脚不动,坡顶沿削进到点处,问至少是多少米(精确到0.1m)?(参考数据:,,)四、当堂训练,巩固新知1.某人沿着倾斜角为的斜坡前进了米,那么他上升的高度是( )A.米 B.米 C.米 D.米2.一个钢球沿坡角的斜坡向上滚动了米,此时钢球距地面的高度是( )米A. B. C. D.某人沿着一山坡向上走了400米,其铅直高度上升了200米,则山坡与水平面的锐角是( )如图,梯形是一堤坝横截面的示意图,坡角,,斜坡,上底.求坝高及下底的长(结果保留根号).五、当堂检测,布置作业1.河堤的横断面如图所示,堤高,迎水斜坡的长为,那么斜坡的坡度是多少?2. 如图,水库大坝的横断面是梯形,坝顶宽6m,坝高24m,斜坡的坡角 为,斜坡的坡角的正切值为,则坡底的长为多少m?3.如图所示,铁路的路基横断面是等腰梯形,斜坡的坡度为,坡面 的水平宽度为,基面宽为,则 , , . 六、合作交流,共同提高: 1.如图,梯形是一堤坝横截面的示意图,坡角,,斜坡,要求下底BC的长,还需知道什么条件?
课后拓展案
随着社会的发展,人们对防 ( http: / / www.21cnjy.com )洪的意识越来越强,今年为了提前做好防洪准备工作,某市正在长江边某处常出现险情的河段修建一防洪大坝,其横断面为梯形ABCD,如图7所示,根据图中数据计算坝底CD的宽度(结果保留根号).
A
B
C
260
上弦
中
柱
A
D
B
C
跨度
D
A
B
C
60
45
东
60°
B
C
A
北
东
D
B
E
A
C
A
D
C
B
北
东
北
B
A
C
D
C
B
A
东
图1
A
E
F
D
C
B
A
D
C
B
24
C
B
A
D
6m
A
C
B
A
D
C
F
E
B
A
D
F
E
B
10m
9m
45°
60°
C
内容 九下教科书53---57页 主备人
学习目标 1.明确仰角、俯角的概念,并能将之灵活应用于实际生活;2.能从实际问题中抽象出几何模型,并能借助计算器解决问题;3.运用三角比的有关知识来解决实际应用问题.
重点 运用三角比的有关知识来解决实际应用问题.
难点 从实际问题中抽象出恰当的几何模型,用三角比的有关知识来解决.
学前预习案
预习课本P53—P55 请完成下列问题 ①结合2—12示意图会画出铅垂线、仰角、俯角、水平线、视线的示意图;②根据例2的实际问题写出已知条件和结论。运用学过的数学方法,画出适应的解直角三角形的模型。③结合例1,写出已知和求解。
课堂学习案
一、创设情境,导入新课东方明珠塔是上海市的一个标志性建筑. 为了测量东方明珠塔的高度,小亮和同学们在距离东方明珠塔 200 m 处的地面上,安放高 1.20 m 的测角仪支架,测得东方明珠塔顶的仰角为 60°48' . 根据测量的结果,小亮画了一张示意图(图 2-11),其中 AB 表示东方明珠塔,DC 为测角仪的支架,DC = 1.20 m,CB= 200 m,∠ADE = 60°48' .利用上述数据,你能求出 AB 的长吗?与同学交流.二、自主探究,归纳新知1.读一读课本54页小资料:在实际测量中 ( http: / / www.21cnjy.com ),从低处观测高处的目标时,_________与_________所成的锐角叫做_________,从高处观测低处的目标时,_______与________所成的锐角叫做______.例1 如图 2-14,一架直升飞机执行海上搜救任务,在空中 A 处发现海面上有一目标 B,仪器显示这时飞机的高度为 1.5 km,飞机距目标 4.5 km.求飞机在 A 处观测目标 B 的俯角(精确到 1')例2 武汉长江二桥为斜拉索桥( 图2-15),AB 和 AC 分别是直立塔 AD 左右两边的两根最长的钢索. 已知 AB = AC, ( http: / / www.21cnjy.com )BC = 100 m,AB与 BC 的夹角为 30°,求钢索 AB 的长及直立塔 AD的高(精确到 0.1 m).合作交流,完善新知把实际问题转化为解直角三角形问题,关键是找 ( http: / / www.21cnjy.com )出实际问题中的_____________,这一解答过程的思路是:有关实际问题转化_____________ ,求出有关的边或 得出问题答案。四、精讲点拨,深化新知如图,厂房屋顶人字架的跨度为10米,上弦AB=BD,∠A=260,求中柱BC和上弦AB的长.(精确到0.01米)五、当堂训练,巩固新知1、如图,小明想测量塔CD的高度。他在A处仰望塔顶,测得仰角为45゜,再往塔的方向前进50m至B处,测得仰角为60゜,那么该塔有多高?(小明的身高忽略不计,结果精确到1m)2、 一颗大树在一次强烈的地震中于C处折断倒下,树顶落在地面B处,测得B处与树的底端A相距25米,∠ABC=24°①求大树折倒下部分BC的长度。(精确到1米)六、当堂检测,布置作业1、一灯柱AB被一钢缆CD ( http: / / www.21cnjy.com )固定,CD与地面成40 夹角,且DB=5m,在C点上方2m处加固另一条钢缆ED,那么钢缆ED的长度为多少?(结果精确到0、01m)2、(1) 从地面上C、D两处看山顶A ( http: / / www.21cnjy.com ),仰角分别是30°和45°,从山顶A看地面上的D处时,则俯角是__________d度。若BD=m米,则山高AB=________米,山顶A距C的距离AC=_____________米. ( http: / / www.21cnjy.com )(2)在坡屋顶的设计图中AB=AC,屋顶的宽度l为10米,坡角(为35°,则坡屋顶的高度h为______________米。
课后拓展案
如图河对岸有水塔AB.在C处测得塔顶的仰角为30°,向塔前进12m到达D,在D处测得A的仰角为45°,求塔高.
课题 2.5 解直角三角形(第二课时) 课型 新授
内容 九下教科书56---57页 主备人 张小勇
学习目标 进一歩掌握解直角三角形的方法。能熟练地应用解直角三角形的知识解决有关航海的实际问题。
重点 重点:熟练掌握方位角的概念,掌握特殊三角比
难点 难点:熟练掌握解直角三角形的基本方法
学前预习案
1、下图,用连线将左边表示的方向与右边表示点的字母连接起来。 ( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com )2、如图,一艘轮船航行到B处时,灯 ( http: / / www.21cnjy.com )塔A在船的北偏东60°的方向,轮船从B处向正东方向行驶2400m到达C处,此时灯塔A在船的正北方向,求C处与灯塔A的距离(精确到1m)。
课堂学习案
一、创设情境,导入新课如图,一船从A点出发,沿北偏东方向航行12海里到达B点,然后又沿南偏东方向航行16海里到达C点,那么从C点再航行多远才能直接返回出发点A(精确到0.1海里) 自主探究,归纳新知1、如图所示,某船从点向正东方向航行,在处望见灯塔在东北方向,前进到处望见灯塔在北偏西方向,又航行了半小时到处,望见灯塔恰在西北方向,若船速为每小时海里,求,两点间距离.合作交流,完善新知2.如图,海关某缉私艇巡逻到达处时,接到情报,在处北偏西方向的处发现一艘可疑船只,正以的速度向正东方向前进,上级命令对可疑船只进行检查,该艇立即沿北偏西的方向快速前进,经过的航行,正好在处截住可疑船只,求该艇的速度.(结果保留到整数)四、精讲点拨,深化新知如图,在港口的正东15海里处有一观测站,一艘货船从处向正北方向航行,当货船航行到处时,从观测站测得货船的方向为北偏西,0.5h后,货船到这处,此时从处测得货船的方向为北偏西.求货船航行的速度(精确到1海里,).五、当堂训练,巩固新知1.海中有一个小岛,它的周围8海里内有暗礁,渔船跟踪鱼群由西向东航行,在点测得小岛在北偏东,航行12海里到达点,这时小岛在北偏东,如果渔船不改变方向航行,继续向东捕捞,有没有触礁的危险?请说明理由.当堂检测,布置作业入夏以来,松花江哈尔滨段水位不断下 ( http: / / www.21cnjy.com )降,达到历史最低水位,一条船在松花江某水段自西向东沿直线航行,在A处测得航标C在北偏东60°方向上,前进100米到达B处,又测得航标C在北偏东45°方向上,如图,在以航标C为圆心,120米长为半径的圆形区域内有浅滩,如果这条船继续前进,是否有被浅滩阻碍的危险?
课后拓展案
2.如图,一艘渔船正以每小时的速度由西向东航行,在处看见小岛在船的北偏东方向上,后,渔船行至处,此时看见小岛在船的北偏东方向上.若以小岛的中心周围的范围内是危险区,问:这艘渔船继续向东航行是否有进入危险区的可能?
课题 2.5 解直角三角形的应用(第三课时) 课型 新授
内容 九下教科书58页 主备人
学习目标 1.认识坡角、坡度,并能结合实际标准角度。2.能应用解直角三角形的知识解决实际问题
重点 直角三角形的解法
难点 三角比在解直角三角形中的灵活运用
学前预习案
1、阅读课本58页中有关坡度的内容,说一说什么是坡角,什么是坡度或坡比,坡度与坡角的正切有什么关系 请把重点知识写在下面._______________________________________________________________________________________________________________________________________________________________________________________________________________2、看例4的解答过程,你知道如何构造直角三角形来解决实际问题吗?需要做什么辅助线?
课堂学习案
一、创设情境,导入新课二、自主探究,归纳新知例4、某地计划在河流的上游 ( http: / / www.21cnjy.com )修建一条拦水大坝,大坝的横断面ABCD是梯形(如图),坝顶宽BC=6米,坝高25米,迎水坡AB的坡度i=1:3,背水坡CD的坡度i=1:2.5.(1)求斜坡AB和CD的长(精确到0.01米);(2)求拦水大坝的底面AD的宽.三、精讲点拨,深化新知1、某校教学楼后面紧邻着一个土坡,坡上面是一块平地,如图所示,,斜坡长22m,坡角,为了防止山体滑坡,保障安全,学校决定对该土坡进行改造.地质人员勘测,当坡角不超过时,可确保山体不滑坡.(1)求改造前坡顶与地面的距离的长(精确到0.1m);(2)为确保安全,学校计划改造时保持坡脚不动,坡顶沿削进到点处,问至少是多少米(精确到0.1m)?(参考数据:,,)四、当堂训练,巩固新知1.某人沿着倾斜角为的斜坡前进了米,那么他上升的高度是( )A.米 B.米 C.米 D.米2.一个钢球沿坡角的斜坡向上滚动了米,此时钢球距地面的高度是( )米A. B. C. D.某人沿着一山坡向上走了400米,其铅直高度上升了200米,则山坡与水平面的锐角是( )如图,梯形是一堤坝横截面的示意图,坡角,,斜坡,上底.求坝高及下底的长(结果保留根号).五、当堂检测,布置作业1.河堤的横断面如图所示,堤高,迎水斜坡的长为,那么斜坡的坡度是多少?2. 如图,水库大坝的横断面是梯形,坝顶宽6m,坝高24m,斜坡的坡角 为,斜坡的坡角的正切值为,则坡底的长为多少m?3.如图所示,铁路的路基横断面是等腰梯形,斜坡的坡度为,坡面 的水平宽度为,基面宽为,则 , , . 六、合作交流,共同提高: 1.如图,梯形是一堤坝横截面的示意图,坡角,,斜坡,要求下底BC的长,还需知道什么条件?
课后拓展案
随着社会的发展,人们对防 ( http: / / www.21cnjy.com )洪的意识越来越强,今年为了提前做好防洪准备工作,某市正在长江边某处常出现险情的河段修建一防洪大坝,其横断面为梯形ABCD,如图7所示,根据图中数据计算坝底CD的宽度(结果保留根号).
A
B
C
260
上弦
中
柱
A
D
B
C
跨度
D
A
B
C
60
45
东
60°
B
C
A
北
东
D
B
E
A
C
A
D
C
B
北
东
北
B
A
C
D
C
B
A
东
图1
A
E
F
D
C
B
A
D
C
B
24
C
B
A
D
6m
A
C
B
A
D
C
F
E
B
A
D
F
E
B
10m
9m
45°
60°
C
同课章节目录
- 第1章 图形的相似
- 1.1 相似多边形
- 1.2 怎样判定三角形相似
- 1.3 相似三角形的性质
- 1.4 图形的位似
- 第2章 解直角三角形
- 2.1 锐角三角比
- 2.2 30°,45°,60°角的三角比
- 2.3 用计算器求锐角三角比
- 2.4 解直角三角形
- 2.5 解直角三角形的应用
- 第3章 对圆的进一步认识
- 3.1 圆的对称性
- 3.2 确定圆的条件
- 3.3 圆周角
- 3.4 直线与圆的位置关系
- 3.5 三角形的内切圆
- 3.6 弧长及扇形面积的计算
- 3.7 正多边形与圆
- 课题学习 图形变换与图案设计
- 第4章 一元二次方程
- 4.1 一元二次方程
- 4.2 用配方法解一元二次方程
- 4.3 用公式法解一元二次方程
- 4.4 用因式分解法解一元二次方程
- 4.5 一元二次方程的应用
- 4.6 一元二次方程根与系数的关系
