2016届山东省泰安市岱岳区九上数学(青岛版)学案:2.2 30°, 45°, 60°角的三角比
文档属性
| 名称 | 2016届山东省泰安市岱岳区九上数学(青岛版)学案:2.2 30°, 45°, 60°角的三角比 |

|
|
| 格式 | zip | ||
| 文件大小 | 45.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2015-10-26 14:30:58 | ||
图片预览

文档简介
课题 2.2 30°, 45°, 60°角的三角比 课型 新授
内容 九下教科书41---44页 主备人 张小勇
学习目标 1. 理解、记忆、应用30、45、60特殊锐角的三角比。 2.了解互余两角的三角比之间的关系,探索记忆方法。3.体验数形结合的数学方法和自主探索获得知识的学习过程。
重点 含有30°、45°、60°角的三角函数值的计算
难点 如何记忆30°、45°、60°角的三角函数值
学前预习案
自学提纲:一个直角三角形中,一个锐角正弦是怎么定义的? ;一个锐角余弦是怎么定义的? ;一个锐角正切是怎么定义的? ;
课堂学习案
一、创设情境,导入新课苏州虎丘塔是我国江南著名的园林景点.它始 ( http: / / www.21cnjy.com )建于宋代(961 年),共7 层,高47 . 5 米.由于地基的原因,塔身自400 年前就开始向西北方向倾斜.据测量,至今塔顶的中心偏离底层中心铅垂线已达2 . 3 米,被称为“东方比萨斜塔”.(1)至今虎丘塔塔顶中心距地面多高?
(2)至今虎丘塔塔顶中心偏离底层中心 铅垂线多少度?
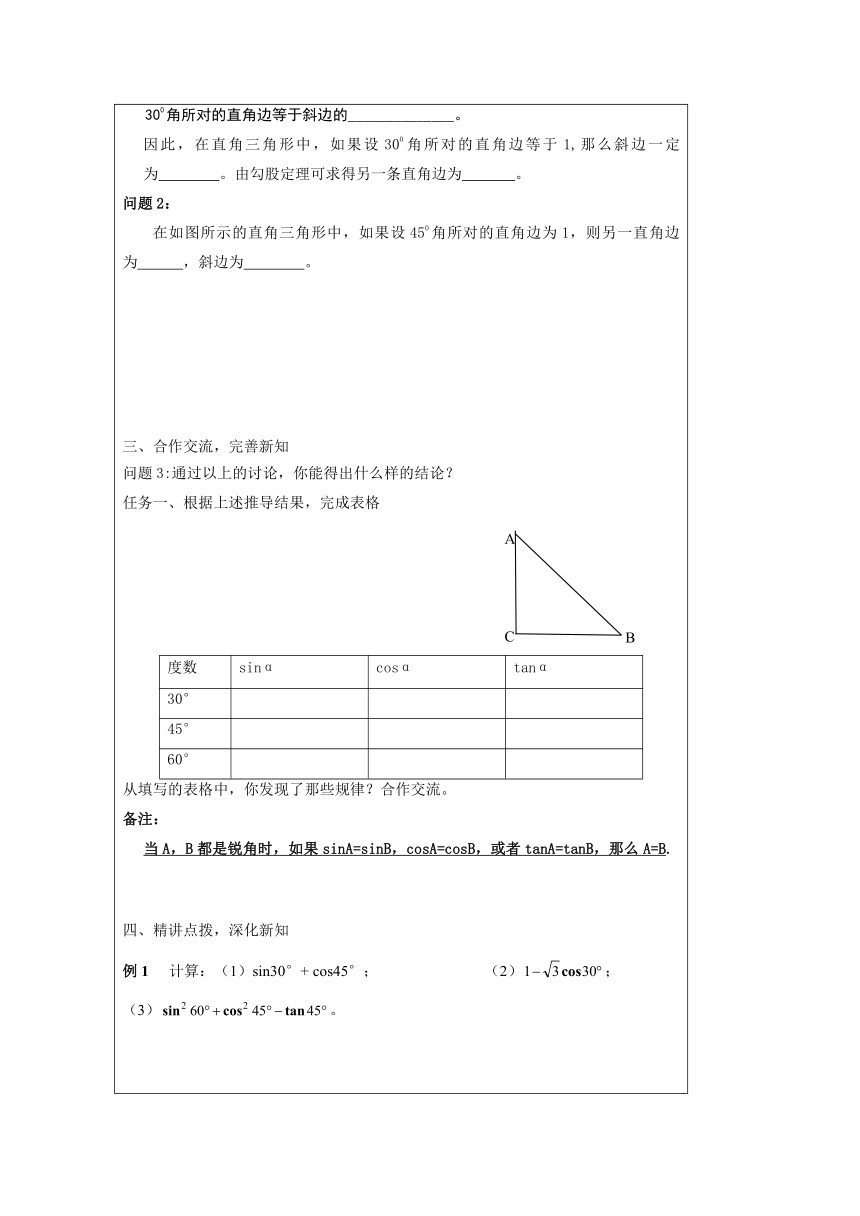
(3)虎丘塔与地平面的倾斜角是多少?自主探究,归纳新知问题1:如图,把两个全等的含有300的三角 ( http: / / www.21cnjy.com )板拼成如图所示的△ADC,思考:△ADC是什么形状的?图中BC的长与AC的长有什么关系?由此得到: 300角所对的直角边等于斜边的______________。因此,在直角三角形中,如果设300角所对的直角边等于1,那么斜边一定为 。由勾股定理可求得另一条直角边为 。问题2: 在如图所示的直角三角形中,如果设450角所对的直角边为1,则另一直角边为 ,斜边为 。合作交流,完善新知问题3:通过以上的讨论,你能得出什么样的结论?任务一、根据上述推导结果,完成表格度数sinαcosαtanα30°45°60°从填写的表格中,你发现了那些规律?合作交流。备注:当A,B都是锐角时,如果sinA=sinB,cosA=cosB,或者tanA=tanB,那么A=B.四、精讲点拨,深化新知计算:(1)sin30°+ cos45°; (2); (3)。填空:(1)已知∠A是锐角,且cosA = ,则∠A = °,sinA = ; (2)已知∠B是锐角,且2cosB = 1,则∠B = °; (3)已知∠A是锐角,且3tanA= 0,则∠A = °;五、当堂训练,巩固新知1、2cos60°的值等于 .2、已知a为锐角,且sin(a-10°)=,则a等于 .3、如果△ABC中,sinA=cosB=,则下列最确切的结论是( )A.△ABC是直角三角形,B.△ABC是等腰三角形,C.△ABC是等腰直角三角形,D.△ABC是锐角三角形4、一个小孩荡秋千,秋千链子的长度为2.5 ( http: / / www.21cnjy.com )m,当秋千向两边摆动时,摆角恰好为60°,且两边的摆动角相同,求它摆至最高位置时与其摆至最低位置时的高度之差。六、当堂检测,布置作业1.(1)(sin60°-tan30°)cos45°= .(2)若,则锐角α= .2.在△ABC中,∠A=75°,2cosB=,则tanC= .3.求下列各式的值.(1) (2)tan30°-sin60°·sin30°(3)cos45°+3tan30°+cos30°+2sin60°-2tan45°(4)4.求适合下列条件的锐角 .(1) (2) (4)
课后拓展案
(1)-sin60°(1-sin30°);(2)+cos45°·cos30°; (3) ; (4).
图1
B
C
A
内容 九下教科书41---44页 主备人 张小勇
学习目标 1. 理解、记忆、应用30、45、60特殊锐角的三角比。 2.了解互余两角的三角比之间的关系,探索记忆方法。3.体验数形结合的数学方法和自主探索获得知识的学习过程。
重点 含有30°、45°、60°角的三角函数值的计算
难点 如何记忆30°、45°、60°角的三角函数值
学前预习案
自学提纲:一个直角三角形中,一个锐角正弦是怎么定义的? ;一个锐角余弦是怎么定义的? ;一个锐角正切是怎么定义的? ;
课堂学习案
一、创设情境,导入新课苏州虎丘塔是我国江南著名的园林景点.它始 ( http: / / www.21cnjy.com )建于宋代(961 年),共7 层,高47 . 5 米.由于地基的原因,塔身自400 年前就开始向西北方向倾斜.据测量,至今塔顶的中心偏离底层中心铅垂线已达2 . 3 米,被称为“东方比萨斜塔”.(1)至今虎丘塔塔顶中心距地面多高?
(2)至今虎丘塔塔顶中心偏离底层中心 铅垂线多少度?
(3)虎丘塔与地平面的倾斜角是多少?自主探究,归纳新知问题1:如图,把两个全等的含有300的三角 ( http: / / www.21cnjy.com )板拼成如图所示的△ADC,思考:△ADC是什么形状的?图中BC的长与AC的长有什么关系?由此得到: 300角所对的直角边等于斜边的______________。因此,在直角三角形中,如果设300角所对的直角边等于1,那么斜边一定为 。由勾股定理可求得另一条直角边为 。问题2: 在如图所示的直角三角形中,如果设450角所对的直角边为1,则另一直角边为 ,斜边为 。合作交流,完善新知问题3:通过以上的讨论,你能得出什么样的结论?任务一、根据上述推导结果,完成表格度数sinαcosαtanα30°45°60°从填写的表格中,你发现了那些规律?合作交流。备注:当A,B都是锐角时,如果sinA=sinB,cosA=cosB,或者tanA=tanB,那么A=B.四、精讲点拨,深化新知计算:(1)sin30°+ cos45°; (2); (3)。填空:(1)已知∠A是锐角,且cosA = ,则∠A = °,sinA = ; (2)已知∠B是锐角,且2cosB = 1,则∠B = °; (3)已知∠A是锐角,且3tanA= 0,则∠A = °;五、当堂训练,巩固新知1、2cos60°的值等于 .2、已知a为锐角,且sin(a-10°)=,则a等于 .3、如果△ABC中,sinA=cosB=,则下列最确切的结论是( )A.△ABC是直角三角形,B.△ABC是等腰三角形,C.△ABC是等腰直角三角形,D.△ABC是锐角三角形4、一个小孩荡秋千,秋千链子的长度为2.5 ( http: / / www.21cnjy.com )m,当秋千向两边摆动时,摆角恰好为60°,且两边的摆动角相同,求它摆至最高位置时与其摆至最低位置时的高度之差。六、当堂检测,布置作业1.(1)(sin60°-tan30°)cos45°= .(2)若,则锐角α= .2.在△ABC中,∠A=75°,2cosB=,则tanC= .3.求下列各式的值.(1) (2)tan30°-sin60°·sin30°(3)cos45°+3tan30°+cos30°+2sin60°-2tan45°(4)4.求适合下列条件的锐角 .(1) (2) (4)
课后拓展案
(1)-sin60°(1-sin30°);(2)+cos45°·cos30°; (3) ; (4).
图1
B
C
A
同课章节目录
- 第1章 图形的相似
- 1.1 相似多边形
- 1.2 怎样判定三角形相似
- 1.3 相似三角形的性质
- 1.4 图形的位似
- 第2章 解直角三角形
- 2.1 锐角三角比
- 2.2 30°,45°,60°角的三角比
- 2.3 用计算器求锐角三角比
- 2.4 解直角三角形
- 2.5 解直角三角形的应用
- 第3章 对圆的进一步认识
- 3.1 圆的对称性
- 3.2 确定圆的条件
- 3.3 圆周角
- 3.4 直线与圆的位置关系
- 3.5 三角形的内切圆
- 3.6 弧长及扇形面积的计算
- 3.7 正多边形与圆
- 课题学习 图形变换与图案设计
- 第4章 一元二次方程
- 4.1 一元二次方程
- 4.2 用配方法解一元二次方程
- 4.3 用公式法解一元二次方程
- 4.4 用因式分解法解一元二次方程
- 4.5 一元二次方程的应用
- 4.6 一元二次方程根与系数的关系
