2016届山东省泰安市岱岳区九上数学(青岛版)学案:2.4 解直角三角形(2课时)
文档属性
| 名称 | 2016届山东省泰安市岱岳区九上数学(青岛版)学案:2.4 解直角三角形(2课时) |

|
|
| 格式 | zip | ||
| 文件大小 | 69.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2015-10-26 00:00:00 | ||
图片预览



文档简介
课题 2.4 解直角三角形(第一课时) 课型 新授
内容 九下教科书49---51页 主备人
学习目标 掌握直角三角形的边角关系,并能综合运用边角关系解决实际问题;明确解直角三角形的意义,会解直角三角形.
重点 解直角三角形所用的关系:三边之间的关系; 2、两锐角之间的关系; 边角之间的关系.
难点 灵活的选择上面的关系式,快捷地沟通未知和已知元素。
学前预习案
课前预习:1、解直角三角形的定义 ; 2、三边之间的关系: ;3、两锐角之间的关系: ; 4、边角之间的关系: .
课堂学习案
一、创设情境,导入新课苏州虎丘塔是我国江南著名的园林景点.它始 ( http: / / www.21cnjy.com )建于宋代(961 年),共7 层,高47 . 5 米.由于地基的原因,塔身自400 年前就开始向西北方向倾斜.据测量,至今塔顶的中心偏离底层中心铅垂线已达2 . 3 米,被称为“东方比萨斜塔”.(1)至今虎丘塔塔顶中心距地面多高?
(2)至今虎丘塔塔顶中心偏离底层中心 铅垂线多少度?
(3)虎丘塔与地平面的倾斜角是多少?自主探究,归纳新知问活动一:自主学习:课本P49—P51 完成导学案自主探究:(已知两边, 求其他元素)在Rt△ABC中,已知∠C=90°,a=17.5 ,c=62.5. 解这个直角三角形。活动二:自主探究 (已知一锐角和一边 ,求:其他元素)在Rt△ABC中,已知∠C=90°,c=128 ,∠B=60°解这个直角三角形合作交流,完善新知解直角三角形的基本类型和方法(1)已知 一角和一边 求其他元素 已知∠A , c 则 b= , a = , ∠B= ; 已知∠A,a 则 b= , c = , ∠B= 。(2)已知两边,求其他元素:已知a , b ,则 c= , sinA= ;cosA= ;tanA= 已知a , c ,则 b= , sinA= ;cosA= ;tanA= 四、精讲点拨,深化新知已知两边,求其他元素:(1)已知a , b, 则 c= , sinA= ;cosA= ;tanA= (2)已知a , c, 则 b= , sinA= ;cosA= ;tanA= 求出三角比,然后根据特殊角的三角比求出角。这就要求同学们特殊角的三角比要记得非常扎实。精讲点拨: 已知 : 一角和一边 ,求:其他元素。(1)已知∠A , c,则 b= , a = , ∠B= . (2)已知∠B,a,则 b= , c = , ∠A= .当堂训练,巩固新知1、在Rt△ABC中,已知∠C=90°,a=12 ,b=24 解这个直角三角形。2、在Rt△ABC中,已知∠C=90°,已知c=15 ,∠B = 60° ,求 a.已知∠A=45°, a =24,求b, c .六、当堂检测,布置作业1、在Rt△ABC中,已知∠A=90°,CB=10,AB=5,则∠B 等于( )A、30° B、45° C、60° D、50°2、在一锐角为30°的直角三角形中,已知斜边长为1,则斜边上的高为( )A、 B、 C、 D、3、在Rt△ABC中,∠C=90°,b=5 sinB =,求 边 a, c的长。
课后拓展案
1、在Rt△ABC中, C=90°,b=6 , 若sinA=, 求边a, c的长。在直角坐标系中,点A的坐标为(4,0),点B在第一象限,∠B=90°,OB=2,求点B的坐标。
课题 2.4 解直角三角形(第二课时) 课型 新授
内容 九下教科书51---53页 主备人
学习目标 1、能够“构造直角三角形”解直角三角形.2、提高分析问题和解决问题的能力。感受数形结合在解题中的作用.
重点 如何构造直角三角形.
难点 如何构造直角三角形.
学前预习案
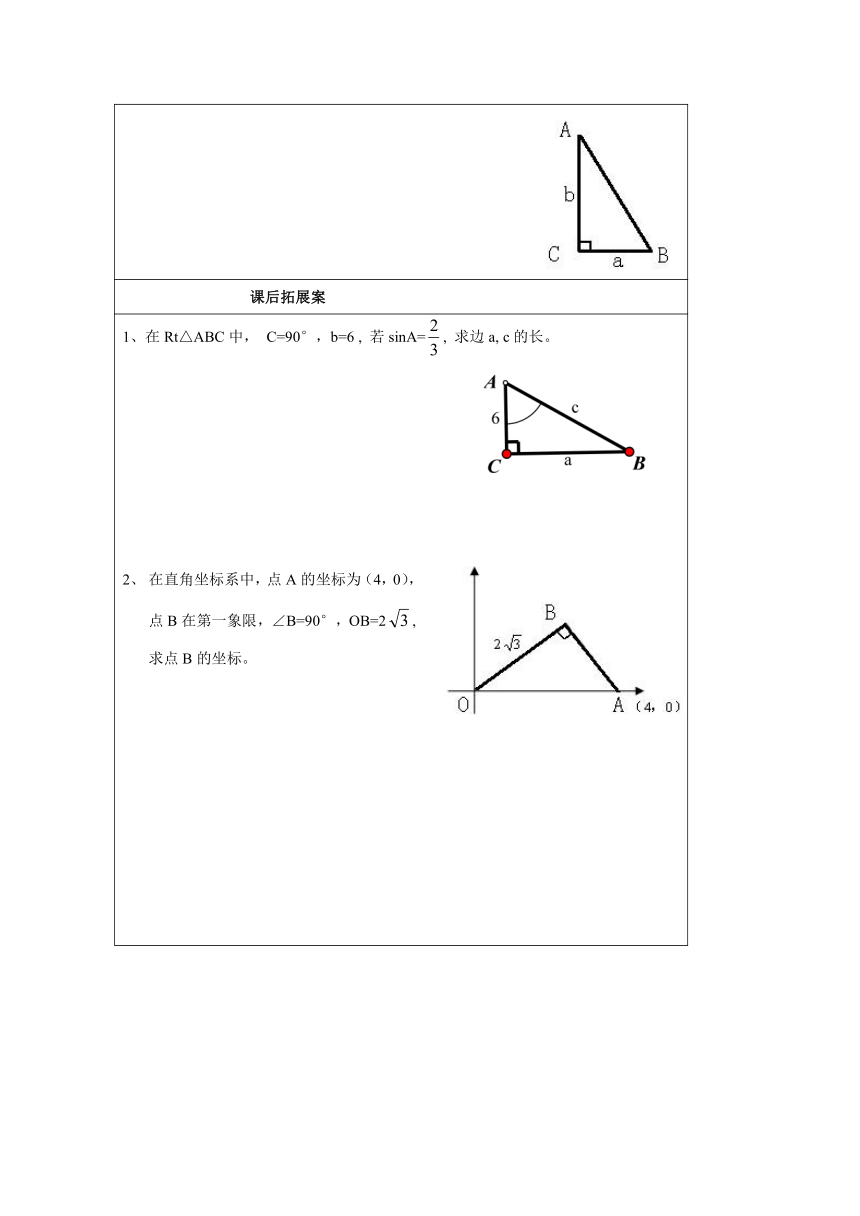
1、什么叫做解直角三角形?2、在Rt△ABC中,如图,∠C=90°,∠A,∠B,∠C的对边分别是a,b,c.(1)角之间的关系: (2)边之间的关系: 。 (3)角与边之间的关系: 3、利用以上关系,已知直角三角形的两个元素(至少一个是 ),就可以解直角三角形了。
课堂学习案
一、创设情境,导入新课如图,为了求河的宽度,在河对岸岸边任意取一 ( http: / / www.21cnjy.com )点A,再在河这边沿河边取两点B、C,使得∠ABC=60°, ∠ACB=45°,量得BC长为30米。(1)求河的宽度;(2)请再设计两种测量河的宽度的方案。自主探究,归纳新知活动一:例3 如图,在△ABC中,已知∠A=60°,∠B=45°,AC=20cm,求AB的长。思考:△ABC不是直角三角形,怎么办?你是怎样构造直角三角形的 你构造的直角三角形能解决这个问题吗?试试看。 活动二:探究例4 已知一个等腰三角形ABC的两边长分别为4和6,求底角的正切值.思考:要求底角的正切值,需在直角三角形中才能解答,怎么办呢? 合作交流,完善新知1、怎样构建直角三角形?应把已知元素和所求元素构建在同一直角三角形中。 2.小组交流构建直角三角形的方法(辅助线的做法):小组内交流统一意见后,考虑解法,能解哪个直角三角形 需要解直角三角形 四、精讲点拨,深化新知1、在直角坐标系中,直线y=x上一点A,OA=5,求点A 的坐标。 ( http: / / www.21cnjy.com )五、当堂训练,巩固新知1.如图,在△ABC中,已知∠B=45°,∠C=75°,AC=2cm,求BC的长。 2.若等边三角形的边长为a,求它的面积六、当堂检测,布置作业1、在△ABC中,已知 ∠A=60 °∠B=45°,AC=20cm,求AB 的长。 2、如图,在△ABC中,若∠B=60°,AB=6cm,,BC=8cm,求(1)AC的长; (2)△ABC的面积。
课后拓展案
1、解决情景导航中的问题
图1
内容 九下教科书49---51页 主备人
学习目标 掌握直角三角形的边角关系,并能综合运用边角关系解决实际问题;明确解直角三角形的意义,会解直角三角形.
重点 解直角三角形所用的关系:三边之间的关系; 2、两锐角之间的关系; 边角之间的关系.
难点 灵活的选择上面的关系式,快捷地沟通未知和已知元素。
学前预习案
课前预习:1、解直角三角形的定义 ; 2、三边之间的关系: ;3、两锐角之间的关系: ; 4、边角之间的关系: .
课堂学习案
一、创设情境,导入新课苏州虎丘塔是我国江南著名的园林景点.它始 ( http: / / www.21cnjy.com )建于宋代(961 年),共7 层,高47 . 5 米.由于地基的原因,塔身自400 年前就开始向西北方向倾斜.据测量,至今塔顶的中心偏离底层中心铅垂线已达2 . 3 米,被称为“东方比萨斜塔”.(1)至今虎丘塔塔顶中心距地面多高?
(2)至今虎丘塔塔顶中心偏离底层中心 铅垂线多少度?
(3)虎丘塔与地平面的倾斜角是多少?自主探究,归纳新知问活动一:自主学习:课本P49—P51 完成导学案自主探究:(已知两边, 求其他元素)在Rt△ABC中,已知∠C=90°,a=17.5 ,c=62.5. 解这个直角三角形。活动二:自主探究 (已知一锐角和一边 ,求:其他元素)在Rt△ABC中,已知∠C=90°,c=128 ,∠B=60°解这个直角三角形合作交流,完善新知解直角三角形的基本类型和方法(1)已知 一角和一边 求其他元素 已知∠A , c 则 b= , a = , ∠B= ; 已知∠A,a 则 b= , c = , ∠B= 。(2)已知两边,求其他元素:已知a , b ,则 c= , sinA= ;cosA= ;tanA= 已知a , c ,则 b= , sinA= ;cosA= ;tanA= 四、精讲点拨,深化新知已知两边,求其他元素:(1)已知a , b, 则 c= , sinA= ;cosA= ;tanA= (2)已知a , c, 则 b= , sinA= ;cosA= ;tanA= 求出三角比,然后根据特殊角的三角比求出角。这就要求同学们特殊角的三角比要记得非常扎实。精讲点拨: 已知 : 一角和一边 ,求:其他元素。(1)已知∠A , c,则 b= , a = , ∠B= . (2)已知∠B,a,则 b= , c = , ∠A= .当堂训练,巩固新知1、在Rt△ABC中,已知∠C=90°,a=12 ,b=24 解这个直角三角形。2、在Rt△ABC中,已知∠C=90°,已知c=15 ,∠B = 60° ,求 a.已知∠A=45°, a =24,求b, c .六、当堂检测,布置作业1、在Rt△ABC中,已知∠A=90°,CB=10,AB=5,则∠B 等于( )A、30° B、45° C、60° D、50°2、在一锐角为30°的直角三角形中,已知斜边长为1,则斜边上的高为( )A、 B、 C、 D、3、在Rt△ABC中,∠C=90°,b=5 sinB =,求 边 a, c的长。
课后拓展案
1、在Rt△ABC中, C=90°,b=6 , 若sinA=, 求边a, c的长。在直角坐标系中,点A的坐标为(4,0),点B在第一象限,∠B=90°,OB=2,求点B的坐标。
课题 2.4 解直角三角形(第二课时) 课型 新授
内容 九下教科书51---53页 主备人
学习目标 1、能够“构造直角三角形”解直角三角形.2、提高分析问题和解决问题的能力。感受数形结合在解题中的作用.
重点 如何构造直角三角形.
难点 如何构造直角三角形.
学前预习案
1、什么叫做解直角三角形?2、在Rt△ABC中,如图,∠C=90°,∠A,∠B,∠C的对边分别是a,b,c.(1)角之间的关系: (2)边之间的关系: 。 (3)角与边之间的关系: 3、利用以上关系,已知直角三角形的两个元素(至少一个是 ),就可以解直角三角形了。
课堂学习案
一、创设情境,导入新课如图,为了求河的宽度,在河对岸岸边任意取一 ( http: / / www.21cnjy.com )点A,再在河这边沿河边取两点B、C,使得∠ABC=60°, ∠ACB=45°,量得BC长为30米。(1)求河的宽度;(2)请再设计两种测量河的宽度的方案。自主探究,归纳新知活动一:例3 如图,在△ABC中,已知∠A=60°,∠B=45°,AC=20cm,求AB的长。思考:△ABC不是直角三角形,怎么办?你是怎样构造直角三角形的 你构造的直角三角形能解决这个问题吗?试试看。 活动二:探究例4 已知一个等腰三角形ABC的两边长分别为4和6,求底角的正切值.思考:要求底角的正切值,需在直角三角形中才能解答,怎么办呢? 合作交流,完善新知1、怎样构建直角三角形?应把已知元素和所求元素构建在同一直角三角形中。 2.小组交流构建直角三角形的方法(辅助线的做法):小组内交流统一意见后,考虑解法,能解哪个直角三角形 需要解直角三角形 四、精讲点拨,深化新知1、在直角坐标系中,直线y=x上一点A,OA=5,求点A 的坐标。 ( http: / / www.21cnjy.com )五、当堂训练,巩固新知1.如图,在△ABC中,已知∠B=45°,∠C=75°,AC=2cm,求BC的长。 2.若等边三角形的边长为a,求它的面积六、当堂检测,布置作业1、在△ABC中,已知 ∠A=60 °∠B=45°,AC=20cm,求AB 的长。 2、如图,在△ABC中,若∠B=60°,AB=6cm,,BC=8cm,求(1)AC的长; (2)△ABC的面积。
课后拓展案
1、解决情景导航中的问题
图1
同课章节目录
- 第1章 图形的相似
- 1.1 相似多边形
- 1.2 怎样判定三角形相似
- 1.3 相似三角形的性质
- 1.4 图形的位似
- 第2章 解直角三角形
- 2.1 锐角三角比
- 2.2 30°,45°,60°角的三角比
- 2.3 用计算器求锐角三角比
- 2.4 解直角三角形
- 2.5 解直角三角形的应用
- 第3章 对圆的进一步认识
- 3.1 圆的对称性
- 3.2 确定圆的条件
- 3.3 圆周角
- 3.4 直线与圆的位置关系
- 3.5 三角形的内切圆
- 3.6 弧长及扇形面积的计算
- 3.7 正多边形与圆
- 课题学习 图形变换与图案设计
- 第4章 一元二次方程
- 4.1 一元二次方程
- 4.2 用配方法解一元二次方程
- 4.3 用公式法解一元二次方程
- 4.4 用因式分解法解一元二次方程
- 4.5 一元二次方程的应用
- 4.6 一元二次方程根与系数的关系
