《数学广角 ——鸡兔同笼》(课件)-四年级数学下册人教版(共18张PPT)
文档属性
| 名称 | 《数学广角 ——鸡兔同笼》(课件)-四年级数学下册人教版(共18张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-04-20 06:29:29 | ||
图片预览






文档简介
(共18张PPT)
第9单元 数学广角
《鸡兔同笼》
经》中记载了一道数学趣题——“鸡兔同笼”问题。
大约一千五百年前,我国古代数学名著《孙子算
谈话导入
今有雉兔同笼,上有三十五头,
下有九十四足,问雉兔各几何?
zhì
雉:野鸡。
笼子里有若干只鸡和兔。从上面数,有35个头,从下面数,有94只脚。鸡和兔各有几只?
鸡有2只脚,兔有4只脚。
鸡和兔共8只,鸡和兔共有26只脚。
笼子里有若干只鸡和兔。从上面数,有8个头,从下面数,有26只脚。鸡和兔各有几只?
自主探究
你知道了哪些数学信息?
题目中隐藏的信息是什么?
1
按照顺序列表试一试。
请你猜一猜鸡、兔的数量。
脚的数量增加2。
每把一只 换成一只 ,
从左至右观察,你有什么发现?
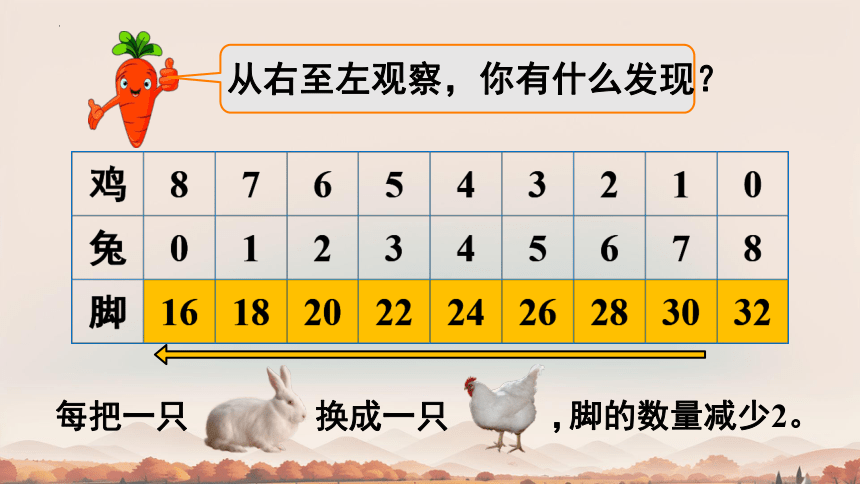
从右至左观察,你有什么发现?
脚的数量减少2。
每把一只 换成一只 ,
2.比实际的26只脚少了( )只。
1.假设8只全是鸡,一共有( )只脚。
汇报展示
16
10
3.一只兔比一只鸡多( )只脚。
4.相差的10只脚,换出了( )只兔。
2
5.鸡有( )只。
5
3
2.比实际的26只脚多了几只?
1.假设8只全是兔,一共有几只脚?
3.一只鸡比一只兔少几只脚?
4.相差的6只脚,能换出几只鸡?
5.兔有几只?
笼子里有若干只鸡和兔,从上面数,有35个头,从下面数,有94只脚。鸡和兔各有几只?
假设笼子里全都是鸡
35×2=70(只)
94-70=24(只)
4-2=2(只)
24÷2=12(只)
兔:
35-12=23(只)
鸡:
答:鸡有23只,兔有12只。
拓展运用
假设笼子里全都是兔
35×4=140(只)
140-94=46(只)
4-2=2(只)
46÷2=23(只)
鸡:
35-23=12(只)
兔:
答:鸡有23只,兔有12只。
笼子里有若干只鸡和兔,从上面数,有35个头,从下面数,有94只脚。鸡和兔各有几只?
3-2=1(个)
26-20=6(个)
10×2=20(个)
假设全是自行车
自行车和三轮车共10辆,总共有26个轮子。自行车和三轮车各有多少辆?
巩固提升
三轮车:6÷1=6(辆)
自行车:10-6=4(辆)
3-2=1(个)
30-26=4(个)
10×3=30(个)
假设全是三轮车
自行车和三轮车共10辆,总共有26个轮子。自行车和三轮车各有多少辆?
巩固提升
自行车:4÷1=4(辆)
三轮车:10-4=6(辆)
今天你有什么收获?
课堂小结
古代解法
《孙子算经》的作者为本题提出了两种解法:
术曰:上置三十五头,下置九十四足。半其足,得四十七,以少减多,再命之,上三除下四,上五除下七,下有一除上三,下有二除上五,即得。
又术曰:上置头,下置足,半其足,以头除足,以足除头,即得。
所谓的“上置”,“下置”指的是将数字按照上下两行摆在筹算盘上。在算筹盘第一行摆上数字三十五,第二行摆上数字九十四,将脚数除以二,此时第一行是三十五,第二行是四十七。用较小的头数减去较多的半脚数,四十减去三十(上三除下四),七减去五(上五除下七)。此时下行是十二,三十五减十二(下一除上三,下二除上五)得二十三。此时第一行剩下的算筹就是鸡的数目,第二行的算筹就是兔的数目。
另一种更简单的描述方法是:在第一行摆好三十五,第二行摆好九十四,将脚数除以2,用头数去减半脚数,用剩下的数(我们现在知道这是兔数)减去头数。这样第一行剩下的是鸡数,第二行剩下兔数。
至于头多于一个的“禽兽问题”,“孙子”给出的解法如下:
术曰:倍足以减首,余半之,即兽;以四乘兽,减足,余半之,即禽。
将脚数乘以两倍(此时禽脚与禽头的系数恰好相同),头数减去两倍脚数,除以二,得到兽的只数(八只),兽的只数乘以四(求出兽的脚数),总脚数减去兽的脚数再除以二,得到禽的只数。
全班一共有38人,共租了8条船,每条船都坐满了。大、小船各租了几条?
大船6人
小船4人
知识过关
假设全租大船
8×6=48(人)
48-38=10(人)
6-4=2(人)
小船:10÷2=5(条)
大船:8-5=3(条)
答:大船租了3条,小船租了5条。
假设全租小船
8×4=32(人)
38-32=6(人)
6-4=2(人)
大船:6÷2=3(条)
小船:8-3=5(条)
答:大船租了3条,小船租了5条。
第9单元 数学广角
《鸡兔同笼》
经》中记载了一道数学趣题——“鸡兔同笼”问题。
大约一千五百年前,我国古代数学名著《孙子算
谈话导入
今有雉兔同笼,上有三十五头,
下有九十四足,问雉兔各几何?
zhì
雉:野鸡。
笼子里有若干只鸡和兔。从上面数,有35个头,从下面数,有94只脚。鸡和兔各有几只?
鸡有2只脚,兔有4只脚。
鸡和兔共8只,鸡和兔共有26只脚。
笼子里有若干只鸡和兔。从上面数,有8个头,从下面数,有26只脚。鸡和兔各有几只?
自主探究
你知道了哪些数学信息?
题目中隐藏的信息是什么?
1
按照顺序列表试一试。
请你猜一猜鸡、兔的数量。
脚的数量增加2。
每把一只 换成一只 ,
从左至右观察,你有什么发现?
从右至左观察,你有什么发现?
脚的数量减少2。
每把一只 换成一只 ,
2.比实际的26只脚少了( )只。
1.假设8只全是鸡,一共有( )只脚。
汇报展示
16
10
3.一只兔比一只鸡多( )只脚。
4.相差的10只脚,换出了( )只兔。
2
5.鸡有( )只。
5
3
2.比实际的26只脚多了几只?
1.假设8只全是兔,一共有几只脚?
3.一只鸡比一只兔少几只脚?
4.相差的6只脚,能换出几只鸡?
5.兔有几只?
笼子里有若干只鸡和兔,从上面数,有35个头,从下面数,有94只脚。鸡和兔各有几只?
假设笼子里全都是鸡
35×2=70(只)
94-70=24(只)
4-2=2(只)
24÷2=12(只)
兔:
35-12=23(只)
鸡:
答:鸡有23只,兔有12只。
拓展运用
假设笼子里全都是兔
35×4=140(只)
140-94=46(只)
4-2=2(只)
46÷2=23(只)
鸡:
35-23=12(只)
兔:
答:鸡有23只,兔有12只。
笼子里有若干只鸡和兔,从上面数,有35个头,从下面数,有94只脚。鸡和兔各有几只?
3-2=1(个)
26-20=6(个)
10×2=20(个)
假设全是自行车
自行车和三轮车共10辆,总共有26个轮子。自行车和三轮车各有多少辆?
巩固提升
三轮车:6÷1=6(辆)
自行车:10-6=4(辆)
3-2=1(个)
30-26=4(个)
10×3=30(个)
假设全是三轮车
自行车和三轮车共10辆,总共有26个轮子。自行车和三轮车各有多少辆?
巩固提升
自行车:4÷1=4(辆)
三轮车:10-4=6(辆)
今天你有什么收获?
课堂小结
古代解法
《孙子算经》的作者为本题提出了两种解法:
术曰:上置三十五头,下置九十四足。半其足,得四十七,以少减多,再命之,上三除下四,上五除下七,下有一除上三,下有二除上五,即得。
又术曰:上置头,下置足,半其足,以头除足,以足除头,即得。
所谓的“上置”,“下置”指的是将数字按照上下两行摆在筹算盘上。在算筹盘第一行摆上数字三十五,第二行摆上数字九十四,将脚数除以二,此时第一行是三十五,第二行是四十七。用较小的头数减去较多的半脚数,四十减去三十(上三除下四),七减去五(上五除下七)。此时下行是十二,三十五减十二(下一除上三,下二除上五)得二十三。此时第一行剩下的算筹就是鸡的数目,第二行的算筹就是兔的数目。
另一种更简单的描述方法是:在第一行摆好三十五,第二行摆好九十四,将脚数除以2,用头数去减半脚数,用剩下的数(我们现在知道这是兔数)减去头数。这样第一行剩下的是鸡数,第二行剩下兔数。
至于头多于一个的“禽兽问题”,“孙子”给出的解法如下:
术曰:倍足以减首,余半之,即兽;以四乘兽,减足,余半之,即禽。
将脚数乘以两倍(此时禽脚与禽头的系数恰好相同),头数减去两倍脚数,除以二,得到兽的只数(八只),兽的只数乘以四(求出兽的脚数),总脚数减去兽的脚数再除以二,得到禽的只数。
全班一共有38人,共租了8条船,每条船都坐满了。大、小船各租了几条?
大船6人
小船4人
知识过关
假设全租大船
8×6=48(人)
48-38=10(人)
6-4=2(人)
小船:10÷2=5(条)
大船:8-5=3(条)
答:大船租了3条,小船租了5条。
假设全租小船
8×4=32(人)
38-32=6(人)
6-4=2(人)
大船:6÷2=3(条)
小船:8-3=5(条)
答:大船租了3条,小船租了5条。
