8.4机械能守恒定律 课件(共30张ppt)物理人教版(2019)必修第二册
文档属性
| 名称 | 8.4机械能守恒定律 课件(共30张ppt)物理人教版(2019)必修第二册 |  | |
| 格式 | pptx | ||
| 文件大小 | 37.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2024-04-17 23:14:34 | ||
图片预览








文档简介
(共30张PPT)
机械能守恒定律
引入新课
通过重力或弹力做功势能和动能相互转化
动能
势能
重力势能:
弹性势能
观察研究对象及过程:
1.全红婵在空中下落
2.弓弦弹射箭
1.重力势能、弹性势能与动能都是机械运动中的能量形式,统称为机械能。
机械能
2.
3 .机械能的性质:
⑴状态量
⑵相对性
⑶系统性
机械能的转化 通过重力或弹力做功实现的。
一、动能与势能的相互转化
摆球摆动过程中,动能与势能的转化遵循什么规律?
动能 势能
二、追寻守恒量
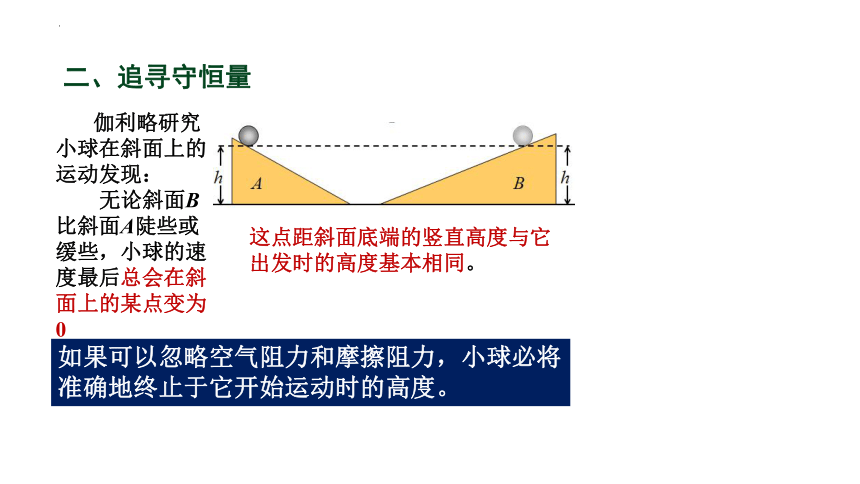
伽利略研究小球在斜面上的运动发现:
无论斜面B比斜面A陡些或缓些,小球的速度最后总会在斜面上的某点变为0
二、追寻守恒量
这点距斜面底端的竖直高度与它出发时的高度基本相同。
如果可以忽略空气阻力和摩擦阻力,小球必将准确地终止于它开始运动时的高度。
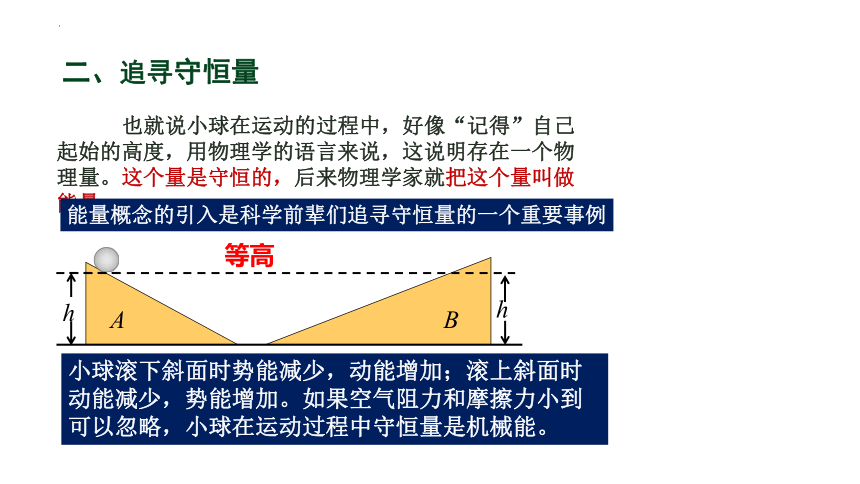
也就说小球在运动的过程中,好像“记得”自己起始的高度,用物理学的语言来说,这说明存在一个物理量。这个量是守恒的,后来物理学家就把这个量叫做能量。
能量概念的引入是科学前辈们追寻守恒量的一个重要事例
A
B
h
二、追寻守恒量
h
等高
小球滚下斜面时势能减少,动能增加;滚上斜面时动能减少,势能增加。如果空气阻力和摩擦力小到可以忽略,小球在运动过程中守恒量是机械能。
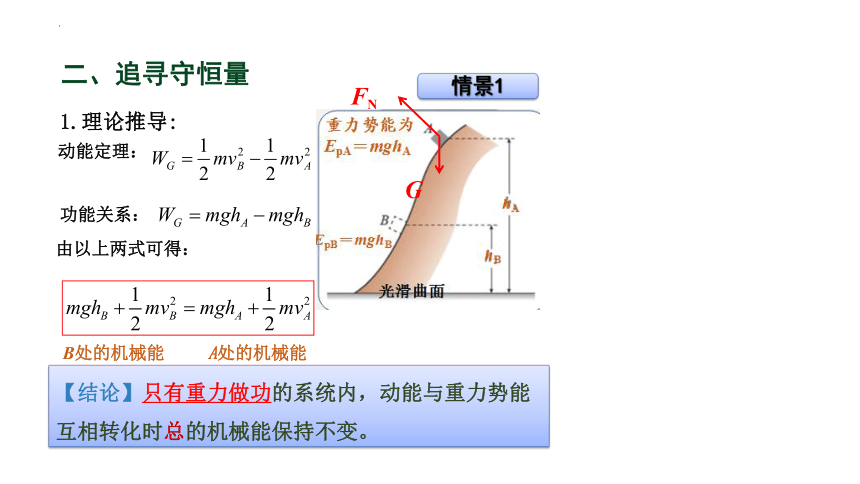
1.理论推导:
动能定理:
功能关系:
由以上两式可得:
【结论】只有重力做功的系统内,动能与重力势能互相转化时总的机械能保持不变。
情景1
二、追寻守恒量
B处的机械能
A处的机械能
G
FN
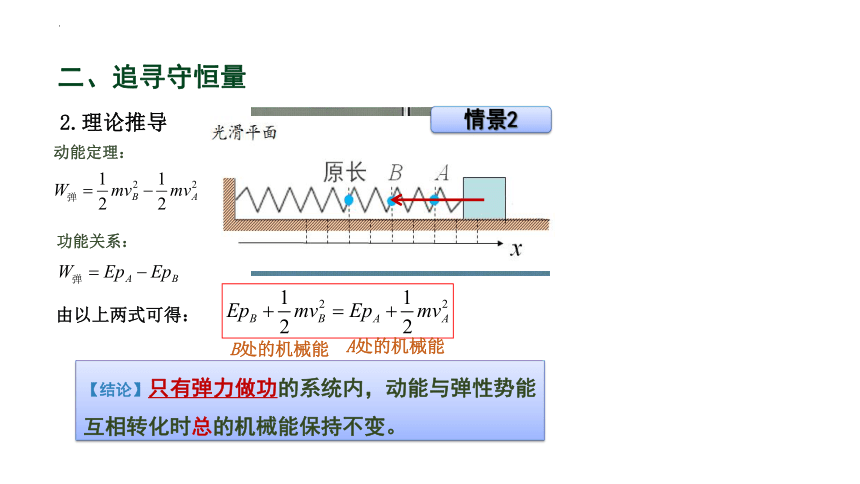
2.理论推导
动能定理:
功能关系:
【结论】只有弹力做功的系统内,动能与弹性势能互相转化时总的机械能保持不变。
由以上两式可得:
B处的机械能
A处的机械能
二、追寻守恒量
情景2
三、机械能守恒定律
在只有重力或弹力做功的物体系统内,动能和势能可以相互转化,而总的机械能保持不变。
3.表达式:
4.机械能守恒的条件:只有重力或弹力做功
1.内容:
E2=E1
EP2+EK2=EP1+EK1
2.研究对象: 系统
在下面列举的各个实例中(除1外都不计空气阻力),哪些过程中系统机械能是守恒的?
1.跳伞运动员带着张开的降落伞在空气中匀速下落
学以致用
2.弓把箭射出后,箭在空中运动
3.全红蝉在空中下落过程
4.全红蝉跃入水中后的运动
机械能
动能
势能
只有重力或弹力做功
总量不变
小结
机械能守恒定律
朱雪莹在蹦床比赛中获得冠军
1.运动过程中她的机械能守恒吗?
2.哪些过程可看成机械能守恒?
课后研究
谢
谢
机械能守恒定律(第二课时)
一个小球在真空中做自由落体运动,另一个同样的小球在黏性较大的油中由静止开始下落。
它们都由高度为 h1 的地方下落到高度为 h2 的地方。在这两种情况下:
重力做的功
重力势能变化
动能的变化
WG=mgΔh
WG=-ΔEp
相等
相等
不相等
1.重力做的功相等吗?
2.重力势能的变化相等吗?
3.动能的变化相等吗?
4.机械能守恒吗?
G
G
F
引入新课
重力做的功
重力势能变化
动能的变化
WG=mgΔh
WG=-ΔEp
相等
相等
不相等
在真空中下落的小球的只有重力做功,故机械能守恒
在油中下落的小球有重力或弹力以外的阻力做功,故机械能不守恒
引入新课
重力做的功
重力势能变化
动能的变化
WG=mgΔh
WG=-ΔEp
相等
相等
不相等
在真空中下落的小球的重力势能全部转化为动能,故机械能守恒
在油中下落的小球一部分重力势能转化为内能,机械能减少,故机械能不守恒
引入新课
一、判断机械能是否守恒的方法
方法1. 从力做功的角度来判断:只有重力或弹力做功,则系统机械能守恒。
方法2. 从能量转化的角度来判断:系统只有动能和势能的相互转化,没有机械能与其他形式的能的转化,则系统机械能守恒。
定 律 理 解
【问题1】朱雪莹在蹦床比赛中获得冠军
⑴运动过程中她的机械能守恒吗?
⑵哪些过程可看成机械能守恒?
定 律 理 解
定 律 应 用
【问题2】 把一个小球用长为l的细绳悬挂起来,将小球拉开一个角度θ,释放后小球运动到最低位置时的速度是多大?(忽略空气阻力)
G
FT
分析 以小球为研究对象
①小球摆动过程中受哪些力?
④小球运动的初、末状态的机械能怎么确定?
取最低点所在水平面为重力势能参考面
初状态A: EP1= mg(l-lcosθ) , EK1=0,
末状态o: EP2=0 , EK2 =
重力、拉力
只有重力做功
机械能守恒
②做功情况 怎样?
③机械能是否守恒 ?
解:小球从A→O,机械能守恒
所以
取最低点所在水平面为重力势能零势面
方法1:
E2=E1
方法2:
解:小球从A O
减小的重力势能
增加的动能
由机械能守恒定律
所以
定 律 应 用
二、应用机械能守恒定律的解决问题思路
1.确定研究对象(物体系统)和要研究的过程
2.判断是否符合机械能守恒的条件:
方法1 研究对象在运动过程中是否只有重力或弹力做功
方法2研究对象在运动过 程中是否只有动能、势能的转化
3.应用机械能守恒定律
解决问题
EP2+EK2=EP1+EK1
定 律 应 用
【问题3】 一条轻绳跨过定滑轮,绳的两端各系一个小球A和B,B球的质量是A球的质量的3倍。用手托住B球,当轻绳刚好被拉紧时,B球离地的高度是h,A球静止于地面,如图所示。现释放B球,当B球刚落地时,求A球的速度大小(定滑轮的质量及滑轮与轴间的摩擦、空气阻力均不计,重力加速度为g)。
研究对象:A、B组成的系统
A上升、B下落到刚要落地的过程中,A与B的速率时刻相等
在B下落A上升的过程中, A、B组成的系统机械能守恒
以地面为零势能参考面
E1=mBgh
系统的初状态的机械能
末状态的机械能
1.确定研究对象(物体系统)和要研究的过程
2.判断是否符合机械能守恒的条件
3.应用机械能守恒定律解决问题
【问题3】 一条轻绳跨过定滑轮,绳的两端各系一个小球A和B,B球的质量是A球的质量的3倍。用手托住B球,当轻绳刚好被拉紧时,B球离地的高度是h,A球静止于地面,如图所示。现释放B球,当B球刚落地时,求A球的速度大小(定滑轮的质量及滑轮与轴间的摩擦均不计,重力加速度为g)。
解:对A、B组成的系统,A上升、B下落到刚要落地的过程
系统机械能守恒,以地面为零势能参考面
由E2=E1可知
所以:v= = =2 m/s
方法1 由E2=E1解决问题
定 律 应 用
【问题3】 一条轻绳跨过定滑轮,绳的两端各系一个小球A和B,B球的质量是A球的质量的3倍。用手托住B球,当轻绳刚好被拉紧时,B球离地的高度是h,A球静止于地面,如图所示。现释放B球,当B球刚落地时,求A球的速度大小(定滑轮的质量及滑轮与轴间的摩擦均不计,重力加速度为g)。
方法1 由E2=E1解决问题
方法2 由ΔEk=-ΔEp解决问题
方法3 由ΔEA=-ΔEB解决问题
定 律 应 用
小结
一、判断机械能是否守恒的方法
二、应用机械能守恒定律的解决问题思路
1.确定研究对象(物体系统)和要研究的过程
2.判断是否符合机械能守恒的条件
3.应用机械能守恒定律解决问题
方法1.从力做功的角度来判断
方法2.从能量转化的角度来判断
课后研究
比较:
1.应用机械能守恒定律解决问题
2.应用牛顿定律解决问题
【问题3】 一条轻绳跨过定滑轮,绳的两端各系一个小球A和B,B球的质量是A球的质量的3倍。用手托住B球,当轻绳刚好被拉紧时,B球离地的高度是h,A球静止于地面,如图所示。现释放B球,当B球刚落地时,求A球的速度大小(定滑轮的质量及滑轮与轴间的摩擦均不计,重力加速度为g)。
谢
谢
大
家
机械能守恒定律
引入新课
通过重力或弹力做功势能和动能相互转化
动能
势能
重力势能:
弹性势能
观察研究对象及过程:
1.全红婵在空中下落
2.弓弦弹射箭
1.重力势能、弹性势能与动能都是机械运动中的能量形式,统称为机械能。
机械能
2.
3 .机械能的性质:
⑴状态量
⑵相对性
⑶系统性
机械能的转化 通过重力或弹力做功实现的。
一、动能与势能的相互转化
摆球摆动过程中,动能与势能的转化遵循什么规律?
动能 势能
二、追寻守恒量
伽利略研究小球在斜面上的运动发现:
无论斜面B比斜面A陡些或缓些,小球的速度最后总会在斜面上的某点变为0
二、追寻守恒量
这点距斜面底端的竖直高度与它出发时的高度基本相同。
如果可以忽略空气阻力和摩擦阻力,小球必将准确地终止于它开始运动时的高度。
也就说小球在运动的过程中,好像“记得”自己起始的高度,用物理学的语言来说,这说明存在一个物理量。这个量是守恒的,后来物理学家就把这个量叫做能量。
能量概念的引入是科学前辈们追寻守恒量的一个重要事例
A
B
h
二、追寻守恒量
h
等高
小球滚下斜面时势能减少,动能增加;滚上斜面时动能减少,势能增加。如果空气阻力和摩擦力小到可以忽略,小球在运动过程中守恒量是机械能。
1.理论推导:
动能定理:
功能关系:
由以上两式可得:
【结论】只有重力做功的系统内,动能与重力势能互相转化时总的机械能保持不变。
情景1
二、追寻守恒量
B处的机械能
A处的机械能
G
FN
2.理论推导
动能定理:
功能关系:
【结论】只有弹力做功的系统内,动能与弹性势能互相转化时总的机械能保持不变。
由以上两式可得:
B处的机械能
A处的机械能
二、追寻守恒量
情景2
三、机械能守恒定律
在只有重力或弹力做功的物体系统内,动能和势能可以相互转化,而总的机械能保持不变。
3.表达式:
4.机械能守恒的条件:只有重力或弹力做功
1.内容:
E2=E1
EP2+EK2=EP1+EK1
2.研究对象: 系统
在下面列举的各个实例中(除1外都不计空气阻力),哪些过程中系统机械能是守恒的?
1.跳伞运动员带着张开的降落伞在空气中匀速下落
学以致用
2.弓把箭射出后,箭在空中运动
3.全红蝉在空中下落过程
4.全红蝉跃入水中后的运动
机械能
动能
势能
只有重力或弹力做功
总量不变
小结
机械能守恒定律
朱雪莹在蹦床比赛中获得冠军
1.运动过程中她的机械能守恒吗?
2.哪些过程可看成机械能守恒?
课后研究
谢
谢
机械能守恒定律(第二课时)
一个小球在真空中做自由落体运动,另一个同样的小球在黏性较大的油中由静止开始下落。
它们都由高度为 h1 的地方下落到高度为 h2 的地方。在这两种情况下:
重力做的功
重力势能变化
动能的变化
WG=mgΔh
WG=-ΔEp
相等
相等
不相等
1.重力做的功相等吗?
2.重力势能的变化相等吗?
3.动能的变化相等吗?
4.机械能守恒吗?
G
G
F
引入新课
重力做的功
重力势能变化
动能的变化
WG=mgΔh
WG=-ΔEp
相等
相等
不相等
在真空中下落的小球的只有重力做功,故机械能守恒
在油中下落的小球有重力或弹力以外的阻力做功,故机械能不守恒
引入新课
重力做的功
重力势能变化
动能的变化
WG=mgΔh
WG=-ΔEp
相等
相等
不相等
在真空中下落的小球的重力势能全部转化为动能,故机械能守恒
在油中下落的小球一部分重力势能转化为内能,机械能减少,故机械能不守恒
引入新课
一、判断机械能是否守恒的方法
方法1. 从力做功的角度来判断:只有重力或弹力做功,则系统机械能守恒。
方法2. 从能量转化的角度来判断:系统只有动能和势能的相互转化,没有机械能与其他形式的能的转化,则系统机械能守恒。
定 律 理 解
【问题1】朱雪莹在蹦床比赛中获得冠军
⑴运动过程中她的机械能守恒吗?
⑵哪些过程可看成机械能守恒?
定 律 理 解
定 律 应 用
【问题2】 把一个小球用长为l的细绳悬挂起来,将小球拉开一个角度θ,释放后小球运动到最低位置时的速度是多大?(忽略空气阻力)
G
FT
分析 以小球为研究对象
①小球摆动过程中受哪些力?
④小球运动的初、末状态的机械能怎么确定?
取最低点所在水平面为重力势能参考面
初状态A: EP1= mg(l-lcosθ) , EK1=0,
末状态o: EP2=0 , EK2 =
重力、拉力
只有重力做功
机械能守恒
②做功情况 怎样?
③机械能是否守恒 ?
解:小球从A→O,机械能守恒
所以
取最低点所在水平面为重力势能零势面
方法1:
E2=E1
方法2:
解:小球从A O
减小的重力势能
增加的动能
由机械能守恒定律
所以
定 律 应 用
二、应用机械能守恒定律的解决问题思路
1.确定研究对象(物体系统)和要研究的过程
2.判断是否符合机械能守恒的条件:
方法1 研究对象在运动过程中是否只有重力或弹力做功
方法2研究对象在运动过 程中是否只有动能、势能的转化
3.应用机械能守恒定律
解决问题
EP2+EK2=EP1+EK1
定 律 应 用
【问题3】 一条轻绳跨过定滑轮,绳的两端各系一个小球A和B,B球的质量是A球的质量的3倍。用手托住B球,当轻绳刚好被拉紧时,B球离地的高度是h,A球静止于地面,如图所示。现释放B球,当B球刚落地时,求A球的速度大小(定滑轮的质量及滑轮与轴间的摩擦、空气阻力均不计,重力加速度为g)。
研究对象:A、B组成的系统
A上升、B下落到刚要落地的过程中,A与B的速率时刻相等
在B下落A上升的过程中, A、B组成的系统机械能守恒
以地面为零势能参考面
E1=mBgh
系统的初状态的机械能
末状态的机械能
1.确定研究对象(物体系统)和要研究的过程
2.判断是否符合机械能守恒的条件
3.应用机械能守恒定律解决问题
【问题3】 一条轻绳跨过定滑轮,绳的两端各系一个小球A和B,B球的质量是A球的质量的3倍。用手托住B球,当轻绳刚好被拉紧时,B球离地的高度是h,A球静止于地面,如图所示。现释放B球,当B球刚落地时,求A球的速度大小(定滑轮的质量及滑轮与轴间的摩擦均不计,重力加速度为g)。
解:对A、B组成的系统,A上升、B下落到刚要落地的过程
系统机械能守恒,以地面为零势能参考面
由E2=E1可知
所以:v= = =2 m/s
方法1 由E2=E1解决问题
定 律 应 用
【问题3】 一条轻绳跨过定滑轮,绳的两端各系一个小球A和B,B球的质量是A球的质量的3倍。用手托住B球,当轻绳刚好被拉紧时,B球离地的高度是h,A球静止于地面,如图所示。现释放B球,当B球刚落地时,求A球的速度大小(定滑轮的质量及滑轮与轴间的摩擦均不计,重力加速度为g)。
方法1 由E2=E1解决问题
方法2 由ΔEk=-ΔEp解决问题
方法3 由ΔEA=-ΔEB解决问题
定 律 应 用
小结
一、判断机械能是否守恒的方法
二、应用机械能守恒定律的解决问题思路
1.确定研究对象(物体系统)和要研究的过程
2.判断是否符合机械能守恒的条件
3.应用机械能守恒定律解决问题
方法1.从力做功的角度来判断
方法2.从能量转化的角度来判断
课后研究
比较:
1.应用机械能守恒定律解决问题
2.应用牛顿定律解决问题
【问题3】 一条轻绳跨过定滑轮,绳的两端各系一个小球A和B,B球的质量是A球的质量的3倍。用手托住B球,当轻绳刚好被拉紧时,B球离地的高度是h,A球静止于地面,如图所示。现释放B球,当B球刚落地时,求A球的速度大小(定滑轮的质量及滑轮与轴间的摩擦均不计,重力加速度为g)。
谢
谢
大
家
