人教版六年级下册数学圆柱、圆锥表面积、体积 复习(课件)(共94张PPT)
文档属性
| 名称 | 人教版六年级下册数学圆柱、圆锥表面积、体积 复习(课件)(共94张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 540.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-04-18 09:46:09 | ||
图片预览


文档简介
(共94张PPT)
圆柱、圆锥表面积、体积 复习
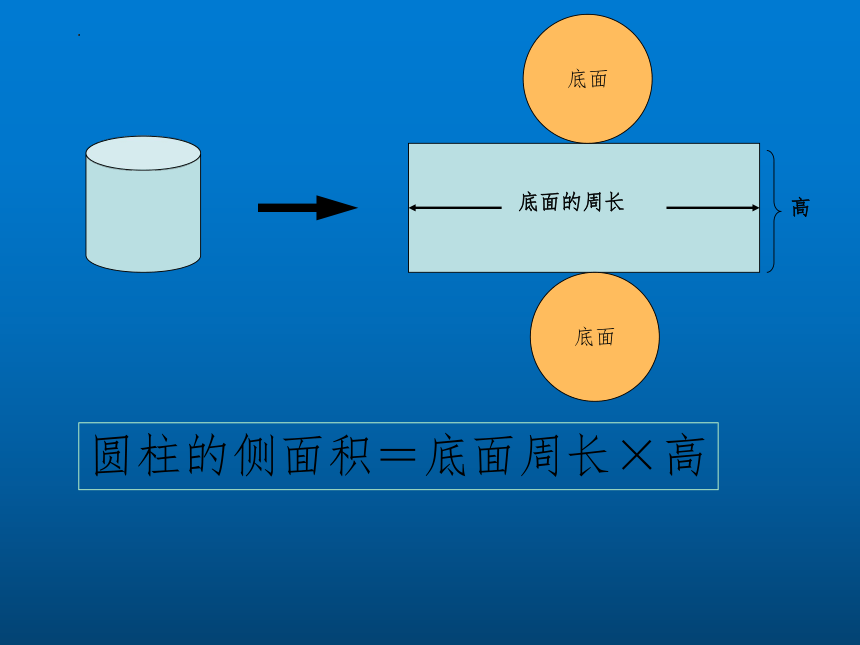
圆柱的侧面积=底面周长×高
底面
底面
高
底面的周长
圆柱的表面积=侧面积+底面面积×2
底面
底面
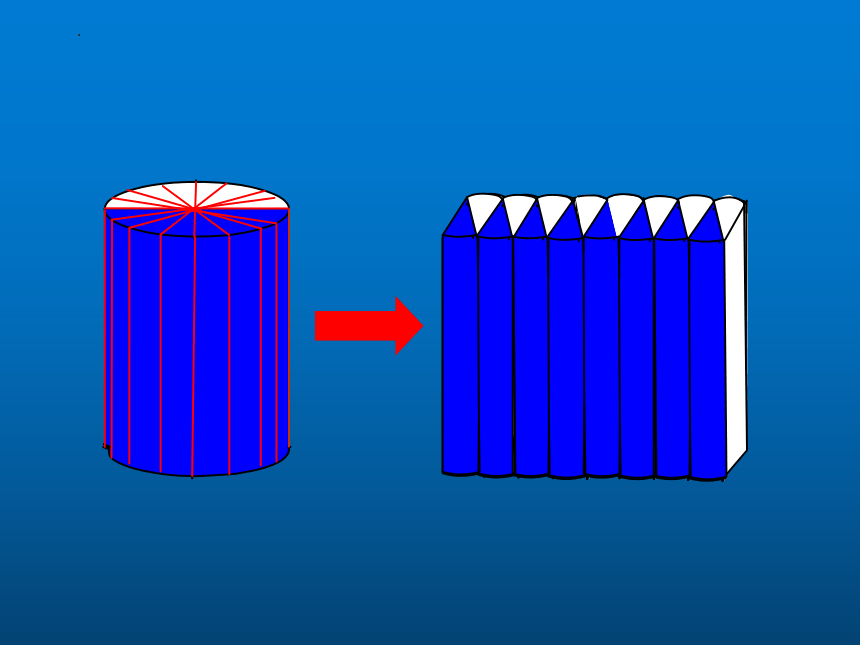
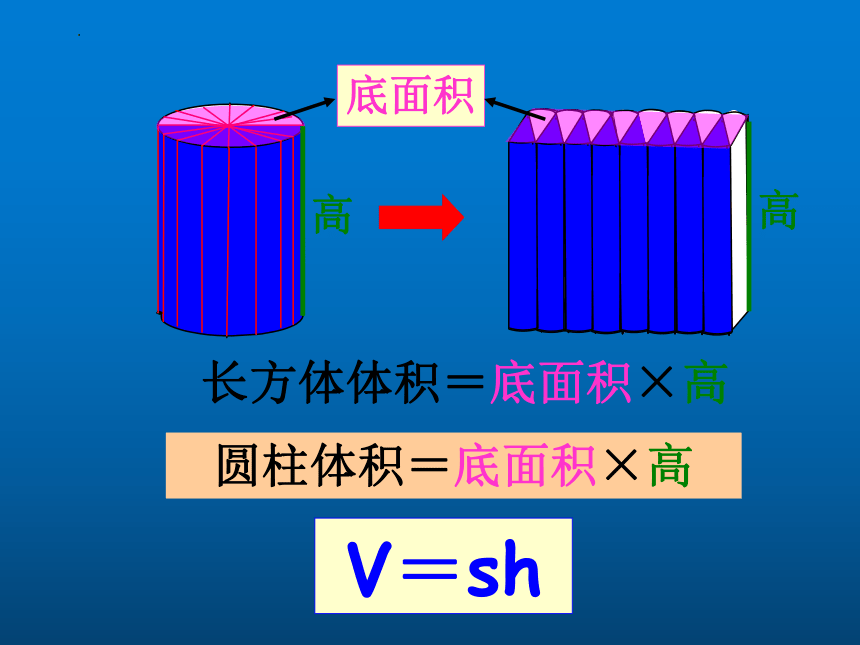
长方体体积=底面积×高
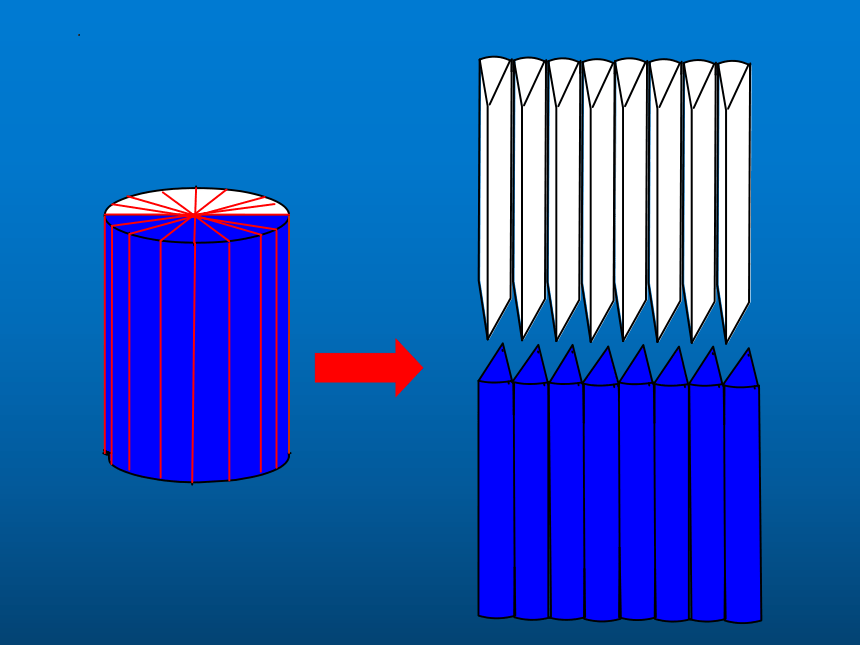
圆柱体积=底面积×高
高
底面积
高
V=sh
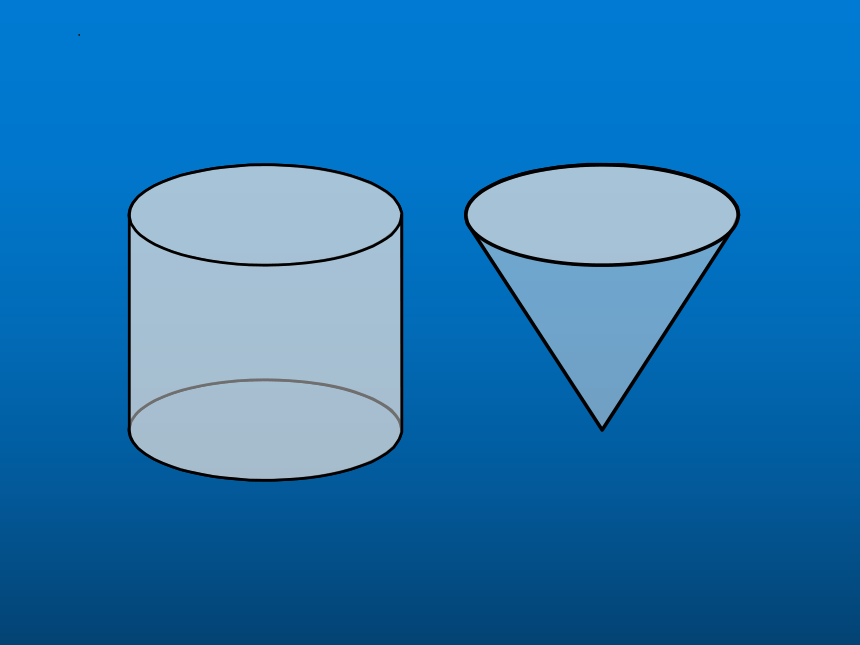
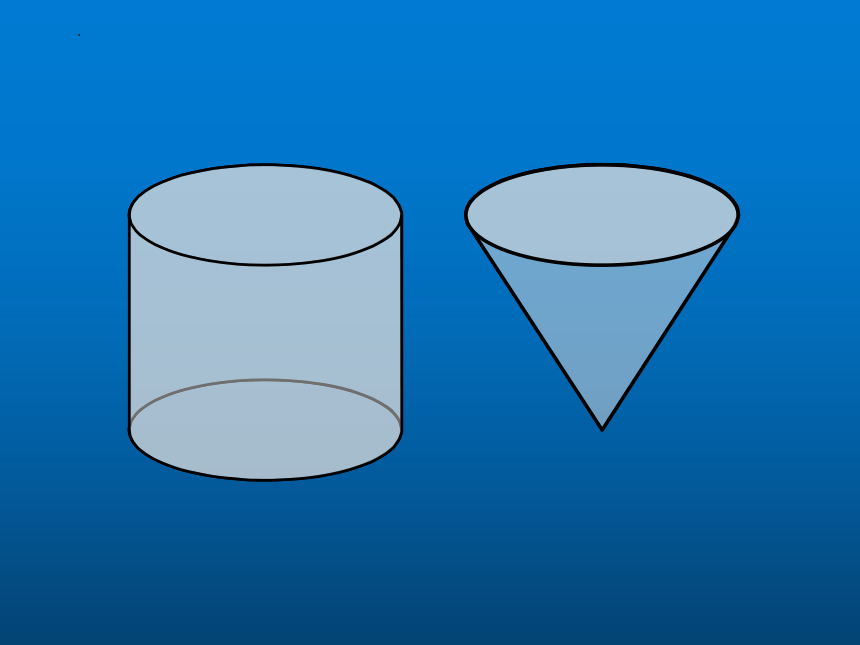
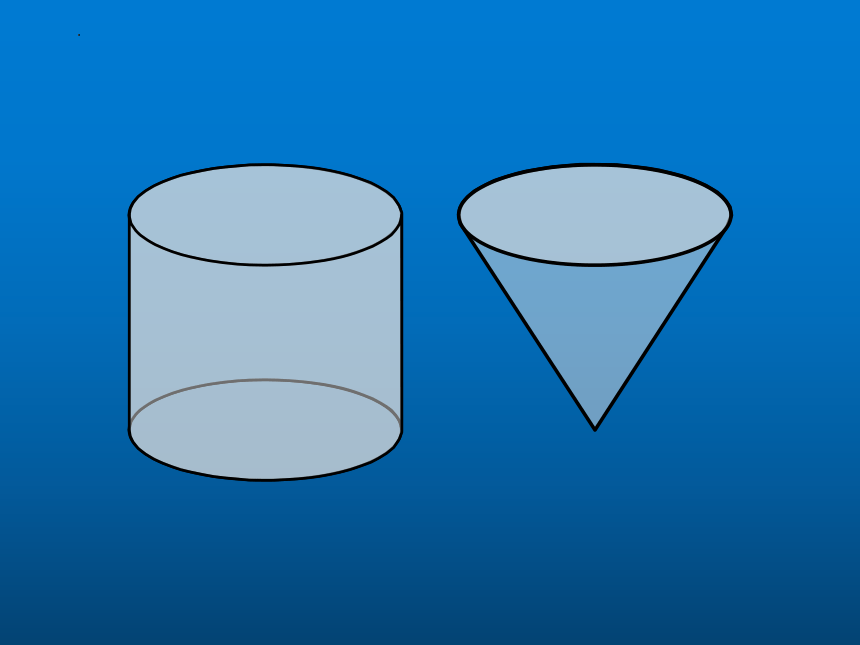
结论:圆柱体积是等底等高 圆锥体积的3倍 ,圆锥体积是等底等高圆柱体积的
推导公式:
V柱=SH
V锥= SH
等底等高
一个圆柱体木料,底面直径20厘米,高30厘米。
1、圆木的侧面积是多少?表面积是多少?
3、圆木的体积是多少?
4、把圆木削成一个最大的圆锥,圆锥的体积是多少?
2、把圆木切开,切成两块,求表面积增加了多少平方厘米?
一个圆柱体木料,底面直径20厘米,高30厘米。
漆
一个圆柱体木料,底面直径20厘米,高30厘米。
横切成两段,表面积增加了多少平方厘米?
切
一个圆柱体木料,底面直径20厘米,高30厘米。
竖切成两块,表面积增加了多少平方厘米?
切
一个圆柱体木料,底面直径20厘米,高30厘米。
削
削成一个最大的圆锥,圆锥的体积是多少立方厘米?
一个圆柱体木料,底面直径20厘米,高30厘米。
挖
挖成一个木桶,求它的容积。
如果内外涂油漆,求涂漆的面积是多少?
(桶壁厚忽略不计)
一、 我来当裁判:
(1)圆柱体的体积与圆锥体的体积比是3 ∶1。
( )
(2)圆柱体的高扩大2倍,体积就扩大2倍。
( )
(3)等底等高的圆柱和圆锥,圆柱的体积比圆锥的体积大2倍. ( )
(4)圆柱体的侧面积等于底面积乘以高。 ( )
(5)圆柱体的底面直径是3厘米,高是9.42厘米,它的侧面展开是一个正形。 ( )
自主检测
二、点兵点将:(填序号)
(1)圆柱体的底面半径扩大3倍,高不变,体积扩大( )
A、3倍 B、9倍 C、6倍
(2)把一个棱长4分米的正方体木块削成一个最大的圆柱体,体积是( )立方分米。
A、50.24 B、100.48 C、64
(3)求长方体,正方体,圆柱体的体积共同的公式是( )
A、V= abh B、V= a3 C、V= Sh
(4)把一个圆柱体的侧面展开得到一个边长4分米的正方形,这个圆柱体的体积是( )立方分米
A、16 B、50.24 C、100.48
(5)把一团圆柱体橡皮泥揉成与它等底的圆锥体,高将( )
A、扩大3倍 B、缩小3倍 C、扩大6倍 D、缩小6倍
自主检测
自主检测
三、还是我聪明:
(1)一个圆柱的侧面展开是边长6.28厘米的正方形。这个圆柱的体积是( )立方厘米。
(2)一根火腿肠,长10厘米,把它横放垂直切成2段后,它的总表面积增加了30平方厘米,原来这根火腿肠的体积是( )立方厘米。
(3)把一个圆柱体木块,削成一个最大的圆锥体后,削去部分的体积是24立方厘米,削成的圆锥体的体积是( )立方厘米。
(4)等底等高的圆柱体和圆锥体的体积比是( ),圆柱的体积比圆锥的体积多( )%,圆锥的体积比圆柱的体积少(----)
自主检测
四、生活小行家
(1)用白铁皮制圆柱形通风筒,每节长80厘米,底面半径5厘米,生产20节这样的通风管,至少需要多少平方米的铁皮?
想一想:生活中还有哪些情况也是求圆柱的侧面积?
(2)一种圆柱体饮料罐,底面周长是18.84厘米,高10厘米,做这样一个饮料罐至少需要多少平方厘米的铁皮?
(3)一个圆锥形谷堆,底面直径4米,高1.5米,
A、求出这堆稻谷的体积是多少立方米?
B、如果每立方米稻谷的质量为800千克,这堆稻谷的质量为多少千克?
(4)一个装满稻谷的粮囤,上面是圆锥形,下面是圆柱形。量得圆柱底面的周长是6.28米,高是2米,圆锥的高是0.45米。这个粮囤能装稻谷多少立方米?如果每立方米稻谷重550千克,这个粮囤能装稻谷多少千克?(得数保留整千克数)
如何测算一个不规则物体(土豆)的体积。
(要求写出解题策略和主要步骤)
奇思妙想
圆柱、圆锥表面积、体积 复习
圆柱的侧面积=底面周长×高
底面
底面
高
底面的周长
圆柱的表面积=侧面积+底面面积×2
底面
底面
长方体体积=底面积×高
圆柱体积=底面积×高
高
底面积
高
V=sh
结论:圆柱体积是等底等高 圆锥体积的3倍 ,圆锥体积是等底等高圆柱体积的
推导公式:
V柱=SH
V锥= SH
等底等高
一个圆柱体木料,底面直径20厘米,高30厘米。
1、圆木的侧面积是多少?表面积是多少?
3、圆木的体积是多少?
4、把圆木削成一个最大的圆锥,圆锥的体积是多少?
2、把圆木切开,切成两块,求表面积增加了多少平方厘米?
一个圆柱体木料,底面直径20厘米,高30厘米。
漆
一个圆柱体木料,底面直径20厘米,高30厘米。
横切成两段,表面积增加了多少平方厘米?
切
一个圆柱体木料,底面直径20厘米,高30厘米。
竖切成两块,表面积增加了多少平方厘米?
切
一个圆柱体木料,底面直径20厘米,高30厘米。
削
削成一个最大的圆锥,圆锥的体积是多少立方厘米?
一个圆柱体木料,底面直径20厘米,高30厘米。
挖
挖成一个木桶,求它的容积。
如果内外涂油漆,求涂漆的面积是多少?
(桶壁厚忽略不计)
一、 我来当裁判:
(1)圆柱体的体积与圆锥体的体积比是3 ∶1。
( )
(2)圆柱体的高扩大2倍,体积就扩大2倍。
( )
(3)等底等高的圆柱和圆锥,圆柱的体积比圆锥的体积大2倍. ( )
(4)圆柱体的侧面积等于底面积乘以高。 ( )
(5)圆柱体的底面直径是3厘米,高是9.42厘米,它的侧面展开是一个正形。 ( )
自主检测
二、点兵点将:(填序号)
(1)圆柱体的底面半径扩大3倍,高不变,体积扩大( )
A、3倍 B、9倍 C、6倍
(2)把一个棱长4分米的正方体木块削成一个最大的圆柱体,体积是( )立方分米。
A、50.24 B、100.48 C、64
(3)求长方体,正方体,圆柱体的体积共同的公式是( )
A、V= abh B、V= a3 C、V= Sh
(4)把一个圆柱体的侧面展开得到一个边长4分米的正方形,这个圆柱体的体积是( )立方分米
A、16 B、50.24 C、100.48
(5)把一团圆柱体橡皮泥揉成与它等底的圆锥体,高将( )
A、扩大3倍 B、缩小3倍 C、扩大6倍 D、缩小6倍
自主检测
自主检测
三、还是我聪明:
(1)一个圆柱的侧面展开是边长6.28厘米的正方形。这个圆柱的体积是( )立方厘米。
(2)一根火腿肠,长10厘米,把它横放垂直切成2段后,它的总表面积增加了30平方厘米,原来这根火腿肠的体积是( )立方厘米。
(3)把一个圆柱体木块,削成一个最大的圆锥体后,削去部分的体积是24立方厘米,削成的圆锥体的体积是( )立方厘米。
(4)等底等高的圆柱体和圆锥体的体积比是( ),圆柱的体积比圆锥的体积多( )%,圆锥的体积比圆柱的体积少(----)
自主检测
四、生活小行家
(1)用白铁皮制圆柱形通风筒,每节长80厘米,底面半径5厘米,生产20节这样的通风管,至少需要多少平方米的铁皮?
想一想:生活中还有哪些情况也是求圆柱的侧面积?
(2)一种圆柱体饮料罐,底面周长是18.84厘米,高10厘米,做这样一个饮料罐至少需要多少平方厘米的铁皮?
(3)一个圆锥形谷堆,底面直径4米,高1.5米,
A、求出这堆稻谷的体积是多少立方米?
B、如果每立方米稻谷的质量为800千克,这堆稻谷的质量为多少千克?
(4)一个装满稻谷的粮囤,上面是圆锥形,下面是圆柱形。量得圆柱底面的周长是6.28米,高是2米,圆锥的高是0.45米。这个粮囤能装稻谷多少立方米?如果每立方米稻谷重550千克,这个粮囤能装稻谷多少千克?(得数保留整千克数)
如何测算一个不规则物体(土豆)的体积。
(要求写出解题策略和主要步骤)
奇思妙想
