数学人教A版(2019)选择性必修第二册4.3.1等比数列通项公式(共23张ppt)
文档属性
| 名称 | 数学人教A版(2019)选择性必修第二册4.3.1等比数列通项公式(共23张ppt) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-04-18 00:00:00 | ||
图片预览








文档简介
(共23张PPT)
等 比 数 列 通 项 公 式
著名数学家华罗庚在其
《数学的用场与发展》
一文中说“宇宙之大,
粒子之微,火箭之速,
化工之巧,地球之变,
生物之谜,日用之繁,
无处不用数学。
1.请同学们回忆等差数列定义?
3.等差数列的通项公式?
如果一个数列从第2项开始,每一项与它前一项的
差都等于同一个常数,那么,这个数列叫做等差数列
2.等差数列定义式?
复习旧知:
袁隆平在培育某水稻新品
种时,培育出第一代120
粒种子,并且从第一代起,
由以后各代的每一粒种子
都可以得到下一代的120粒,
到第5代大约可以得到新品
种的种子多少粒?
世界杂交水稻之父—袁隆平
创设情景,引入课题
庄子曰:“一尺之棰,日取其半,
万世不竭.”意思:“一尺长的木
棒,每日取其一半,永远也取不
完”。如果将“一尺之棰”视为
一份则每日剩下的部分依次为:
创设情景,引入课题
创设情景,引入课题
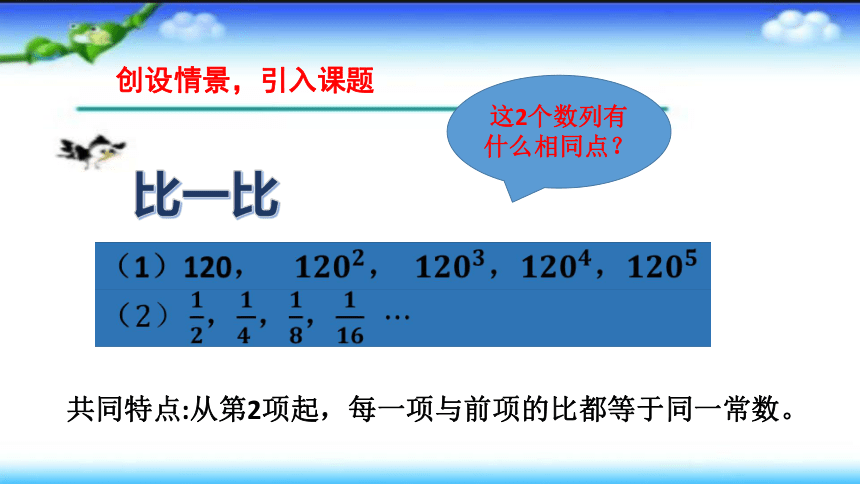
比一比
这2个数列有什么相同点?
共同特点:从第2项起,每一项与前项的比都等于同一常数。
如果一个数列的首项不为零,且从第2项开始,每一项与它前一项的比都等于同一个常数,那么,这个数列叫做等比数列。这个常数叫做等比数列的公比,一般用字母q表示。
等比数列定义
等比数列定义
分析下面几个数列是否是等比数列
是
否
是
否
1) 1,-1,1-1,…………
2) 0,2,0,2,0………..
3) 1,3,5,7,9………..
4) 3,3,3,3,3………..
例
题
解:由于
练
习
2.写出等比数列3,-6,12,-24,……的第5项?
练
习
的公差为d ,则
设等差数列
的公比为q,则
设等比数列
…
依此类推,通过观察可以得到等比数列的通项公式
依此类推,通过观察可以得到等差数列的通项公式
…
推
导
归
纳
例
题
例
题
2. 已知三个数的积为27,且这三个数组
成公比为3的等比数列.求这三个数.
1,3,9
练
习
等比数列
应
用
同学们思考这个合同能签吗?
我们学习了等比数列就可以分析
这里面存在着陷阱,合同是不能签的。
同学们一定要学好数学,来帮助
我们解决实际问题,避免上当啊
小
结
希望同学们勇攀知识高峰
作业:
P19
习题A组 1-4
同学们,作业有困难时,
记得看发给大家的微课哦!
数学——探索世界的有力工具!
用数学的眼光看世界!
数学无处不在!
等 比 数 列 通 项 公 式
著名数学家华罗庚在其
《数学的用场与发展》
一文中说“宇宙之大,
粒子之微,火箭之速,
化工之巧,地球之变,
生物之谜,日用之繁,
无处不用数学。
1.请同学们回忆等差数列定义?
3.等差数列的通项公式?
如果一个数列从第2项开始,每一项与它前一项的
差都等于同一个常数,那么,这个数列叫做等差数列
2.等差数列定义式?
复习旧知:
袁隆平在培育某水稻新品
种时,培育出第一代120
粒种子,并且从第一代起,
由以后各代的每一粒种子
都可以得到下一代的120粒,
到第5代大约可以得到新品
种的种子多少粒?
世界杂交水稻之父—袁隆平
创设情景,引入课题
庄子曰:“一尺之棰,日取其半,
万世不竭.”意思:“一尺长的木
棒,每日取其一半,永远也取不
完”。如果将“一尺之棰”视为
一份则每日剩下的部分依次为:
创设情景,引入课题
创设情景,引入课题
比一比
这2个数列有什么相同点?
共同特点:从第2项起,每一项与前项的比都等于同一常数。
如果一个数列的首项不为零,且从第2项开始,每一项与它前一项的比都等于同一个常数,那么,这个数列叫做等比数列。这个常数叫做等比数列的公比,一般用字母q表示。
等比数列定义
等比数列定义
分析下面几个数列是否是等比数列
是
否
是
否
1) 1,-1,1-1,…………
2) 0,2,0,2,0………..
3) 1,3,5,7,9………..
4) 3,3,3,3,3………..
例
题
解:由于
练
习
2.写出等比数列3,-6,12,-24,……的第5项?
练
习
的公差为d ,则
设等差数列
的公比为q,则
设等比数列
…
依此类推,通过观察可以得到等比数列的通项公式
依此类推,通过观察可以得到等差数列的通项公式
…
推
导
归
纳
例
题
例
题
2. 已知三个数的积为27,且这三个数组
成公比为3的等比数列.求这三个数.
1,3,9
练
习
等比数列
应
用
同学们思考这个合同能签吗?
我们学习了等比数列就可以分析
这里面存在着陷阱,合同是不能签的。
同学们一定要学好数学,来帮助
我们解决实际问题,避免上当啊
小
结
希望同学们勇攀知识高峰
作业:
P19
习题A组 1-4
同学们,作业有困难时,
记得看发给大家的微课哦!
数学——探索世界的有力工具!
用数学的眼光看世界!
数学无处不在!
